平面向量基本定理 Word版含解析
文档属性
| 名称 | 平面向量基本定理 Word版含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 330.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-30 21:23:59 | ||
图片预览



文档简介
绝密★启用前
2.3.1平面向量基本定理
一、选择题
1.【题文】若不共线,且,则( )
A.
B.
C.
D.
2.【题文】设点是平行四边形两对角线的交点,下列向量组:①与;②与;③与;④与,其中可作为该平面其他向量基底的是( )
A.①②
B.①③
C.①④
D.③④
3.【题文】下面三种说法中,正确的是( )
①一个平面内只有一对不共线向量可作为表示
( http: / / www.21cnjy.com )该平面所有向量的基底;②一个平面内有无数多对不共线向量可作为该平面所有向量的基底;③零向量不可作为基底中的向量.
A.①②
B.②③
C.①③
D.①②③
4.【题文】已知向量,其中不共线,则与
的关系是( )
A.不共线
B.共线
C.相等
D.不确定
5.【题文】在△中,依次是的四等分点,以为基底,则等于( )
A.
B.
C.
D.
6.【题文】若,则等于( )
A.
B.
C.
D.
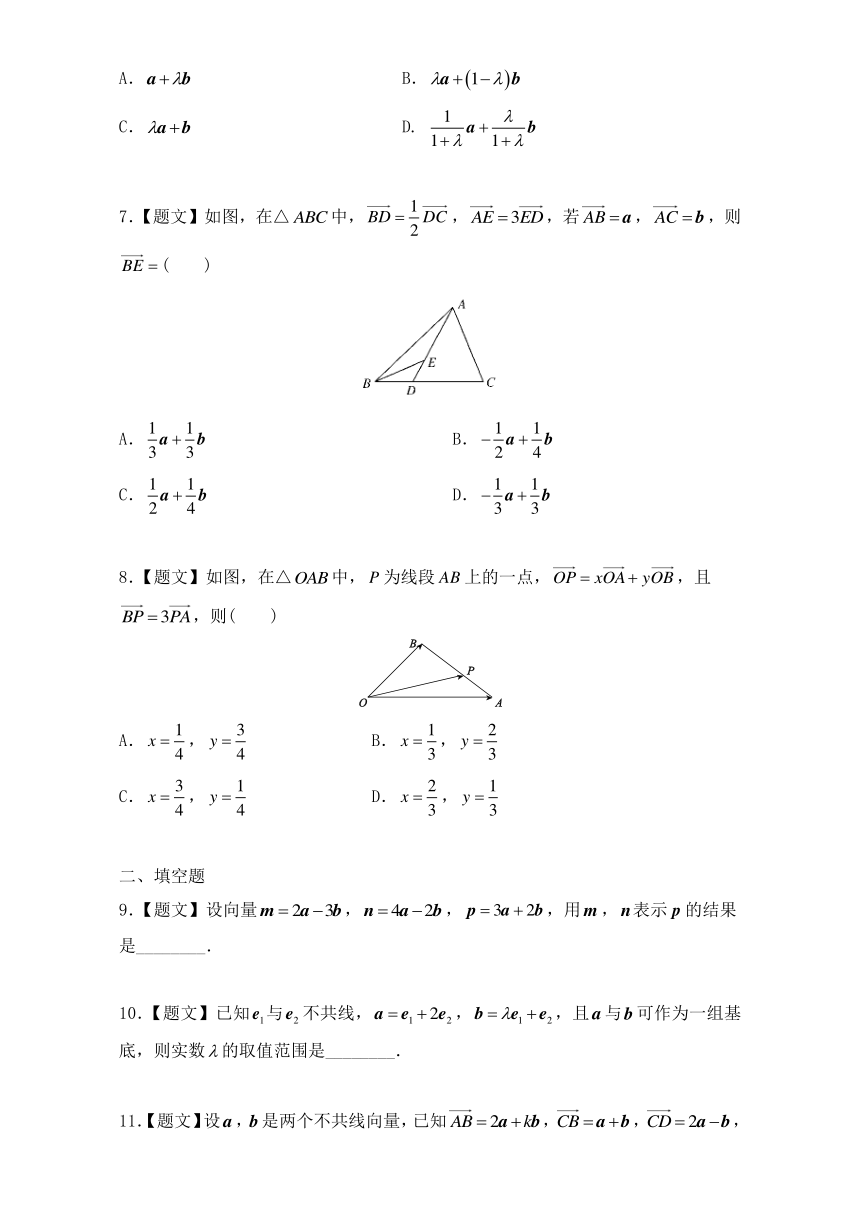
7.【题文】如图,在△中,,,若,,则( )
A.
B.
C.
D.
8.【题文】如图,在△中,为线段上的一点,,且,则( )
A.,
B.,
C.,
D.,
二、填空题
9.【题文】设向量,,,用,表示的结果是________.
10.【题文】已知与不共线,,,且与可作为一组基底,则实数的取值范围是________.
11.【题文】设,是两个不共线向量,已知,,,若、、三点共线,则________.
三、解答题
12.【题文】如图,梯形中,,且,、分别是和的中点,若,,试用,表示、、.
13.【题文】如图,已知△中,为的中点,,为的三等分点,若
,,用,表示,,.
14.【题文】如图所示,平面内有三个向量、、,其中与的夹角为
,与的夹角为,且,,若
,求的值.
2.3.1平面向量基本定理
参考答案及解析
1.
【答案】B
【解析】由平面向量基本定理可知,故选B.
考点:平面向量基本定理.
【题型】选择题
【难度】较易
2.
【答案】B
【解析】易知与不共线,与不共线,故选B.
考点:平面向量基本定理.
【题型】选择题
【难度】较易
3.
【答案】B
【解析】只要平面内一对向量不共线,就可以作为该平面内向量的一组基底,故①不正确,②正确;因为零向量与任意一个向量平行,所以③正确,故选B.
考点:平面向量基本定理.
【题型】选择题
【难度】较易
4.
【答案】B
【解析】,与共线.
考点:平面向量基本定理.
【题型】选择题
【难度】较易
5.
【答案】A
【解析】∵依次是的四等分点,
∴,
∵,
∴.
考点:平面向量基本定理.
【题型】选择题
【难度】一般
6.
【答案】D
【解析】∵,∴,
∴,
∴.
考点:平面向量基本定理.
【题型】选择题
【难度】一般
7.
【答案】B
【解析】∵,∴.
∴,∵,
∴,∴,∴.
∴,∴,∴.
考点:平面向量基本定理.
【题型】选择题
【难度】一般
8.
【答案】C
【解析】∵,
∴,即,
即,又∵,∴,,
故选C.
考点:平面向量基本定理.
【题型】选择题
【难度】一般
9.
【答案】
【解析】设,则
,
所以
考点:平面向量基本定理.
【题型】填空题
【难度】较易
10.
【答案】
【解析】当时,设,则有,即,
∴解得,即当时,.
又与可作为一组基底,∴与不共线,∴.
考点:平面向量基本定理.
【题型】填空题
【难度】一般
11.
【答案】
【解析】∵,,
∴.
∵、、三点共线,
∴存在实数使得,
∴.
又,是两个不共线向量,
∴∴.
考点:平面向量基本定理.
【题型】填空题
【难度】一般
12.
【答案】,,
【解析】如图所示,连接,则四边形是平行四边形.
则,
,
.
考点:平面向量基本定理.
【题型】解答题
【难度】一般
13.
【答案】,,
【解析】
.
.
.
考点:平面向量基本定理.
【题型】解答题
【难度】一般
14.
【答案】
【解析】由题图可知,.
作,,如图,使为平行四边形,由已知得
.
在△中,,
∴.
,∴.
又∵,∴,.
即,,因此.
考点:平面向量基本定理,解三角形.
【题型】解答题
【难度】一般
2.3.1平面向量基本定理
一、选择题
1.【题文】若不共线,且,则( )
A.
B.
C.
D.
2.【题文】设点是平行四边形两对角线的交点,下列向量组:①与;②与;③与;④与,其中可作为该平面其他向量基底的是( )
A.①②
B.①③
C.①④
D.③④
3.【题文】下面三种说法中,正确的是( )
①一个平面内只有一对不共线向量可作为表示
( http: / / www.21cnjy.com )该平面所有向量的基底;②一个平面内有无数多对不共线向量可作为该平面所有向量的基底;③零向量不可作为基底中的向量.
A.①②
B.②③
C.①③
D.①②③
4.【题文】已知向量,其中不共线,则与
的关系是( )
A.不共线
B.共线
C.相等
D.不确定
5.【题文】在△中,依次是的四等分点,以为基底,则等于( )
A.
B.
C.
D.
6.【题文】若,则等于( )
A.
B.
C.
D.
7.【题文】如图,在△中,,,若,,则( )
A.
B.
C.
D.
8.【题文】如图,在△中,为线段上的一点,,且,则( )
A.,
B.,
C.,
D.,
二、填空题
9.【题文】设向量,,,用,表示的结果是________.
10.【题文】已知与不共线,,,且与可作为一组基底,则实数的取值范围是________.
11.【题文】设,是两个不共线向量,已知,,,若、、三点共线,则________.
三、解答题
12.【题文】如图,梯形中,,且,、分别是和的中点,若,,试用,表示、、.
13.【题文】如图,已知△中,为的中点,,为的三等分点,若
,,用,表示,,.
14.【题文】如图所示,平面内有三个向量、、,其中与的夹角为
,与的夹角为,且,,若
,求的值.
2.3.1平面向量基本定理
参考答案及解析
1.
【答案】B
【解析】由平面向量基本定理可知,故选B.
考点:平面向量基本定理.
【题型】选择题
【难度】较易
2.
【答案】B
【解析】易知与不共线,与不共线,故选B.
考点:平面向量基本定理.
【题型】选择题
【难度】较易
3.
【答案】B
【解析】只要平面内一对向量不共线,就可以作为该平面内向量的一组基底,故①不正确,②正确;因为零向量与任意一个向量平行,所以③正确,故选B.
考点:平面向量基本定理.
【题型】选择题
【难度】较易
4.
【答案】B
【解析】,与共线.
考点:平面向量基本定理.
【题型】选择题
【难度】较易
5.
【答案】A
【解析】∵依次是的四等分点,
∴,
∵,
∴.
考点:平面向量基本定理.
【题型】选择题
【难度】一般
6.
【答案】D
【解析】∵,∴,
∴,
∴.
考点:平面向量基本定理.
【题型】选择题
【难度】一般
7.
【答案】B
【解析】∵,∴.
∴,∵,
∴,∴,∴.
∴,∴,∴.
考点:平面向量基本定理.
【题型】选择题
【难度】一般
8.
【答案】C
【解析】∵,
∴,即,
即,又∵,∴,,
故选C.
考点:平面向量基本定理.
【题型】选择题
【难度】一般
9.
【答案】
【解析】设,则
,
所以
考点:平面向量基本定理.
【题型】填空题
【难度】较易
10.
【答案】
【解析】当时,设,则有,即,
∴解得,即当时,.
又与可作为一组基底,∴与不共线,∴.
考点:平面向量基本定理.
【题型】填空题
【难度】一般
11.
【答案】
【解析】∵,,
∴.
∵、、三点共线,
∴存在实数使得,
∴.
又,是两个不共线向量,
∴∴.
考点:平面向量基本定理.
【题型】填空题
【难度】一般
12.
【答案】,,
【解析】如图所示,连接,则四边形是平行四边形.
则,
,
.
考点:平面向量基本定理.
【题型】解答题
【难度】一般
13.
【答案】,,
【解析】
.
.
.
考点:平面向量基本定理.
【题型】解答题
【难度】一般
14.
【答案】
【解析】由题图可知,.
作,,如图,使为平行四边形,由已知得
.
在△中,,
∴.
,∴.
又∵,∴,.
即,,因此.
考点:平面向量基本定理,解三角形.
【题型】解答题
【难度】一般
