14.1.1 同底数幂的乘法课件

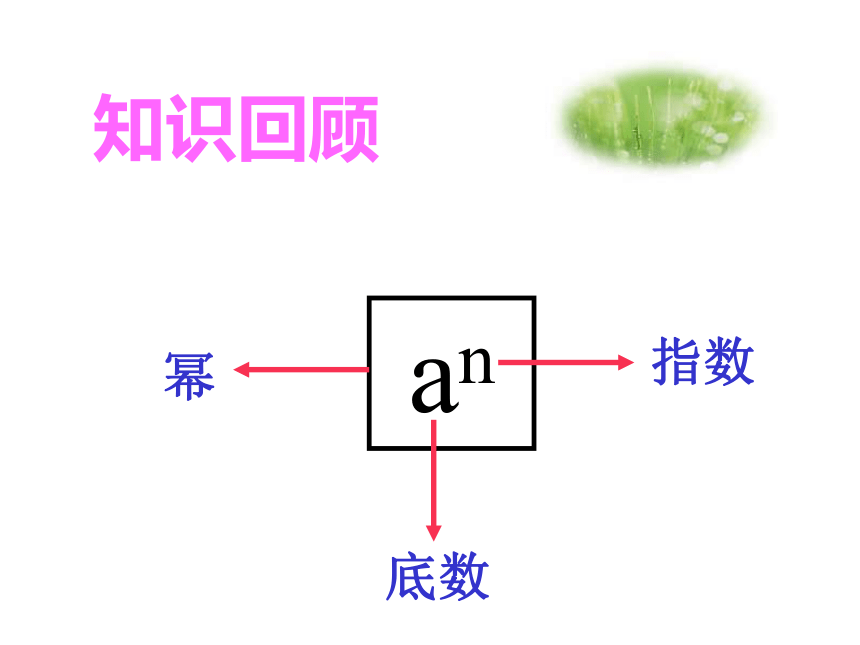
课件23张PPT。 1、2×2 ×2=2( ) 2、a·a·a·a·a = a( ) 35n①什么叫乘方?②乘方的结果叫做什么?知识回顾an知识回顾知识回顾说出am的乘法意义,并将下列各式写成乘法形式:(1) 108(2) (-2)4=10×10×10×10×10×10×10×10=(-2)×(-2)×(-2)×(-2)如108 ×105 =?提出问题那么怎么去求幂与幂之间的乘积呢?试一试：=27 (乘方的意义)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
= 5 × 5 × 5 × 5 × 5 × 5 × 5
=57=(2 ×2 ×2) ×(2 ×2 ×2 ×2) (乘方的意义)= 2 ×2 ×2 ×2 × 2 ×2 ×2 (乘法结合律)=a7 (乘方的意义)继续探索：(3) a3 · a4=(a · a · a) (a · a · a · a) (乘方的意义)= a · a · a · a · a · a · a (乘法结合律) 这几道题有什么共同的特点呢?计算的结果有什么规律吗?(1)23 ×24=a7=27 (2)53×54=57(3)a3 · a4=(a · a · a) (a · a · a · a)=(2 ×2 ×2) ×(2 ×2 ×2 ×2)=(5 × 5 × 5) ×(5 × 5 × 5 × 5) 如果把(3)中指数3、4换成正整数m、n，你能得出am · an的结果吗？(1)23 ×24=a7=27 (2)53×54=57(3)a3 · a4=(a · a · a) (a · a · a · a)=(2 ×2 ×2) ×(2 ×2 ×2 ×2)=(5 × 5 × 5) ×(5 × 5 × 5 × 5) am · an =m个an个a= aa…a=am+n(m+n)个a即:am · an = am+n (当m、n都是正整数)（aa…a）（aa…a）（乘方的意义）（乘法结合律）（乘方的意义）知识推导am · an = am+n (当m、n都是正整数)同底数幂相乘，底数　　，指数　　。不变相加 同底数幂的乘法公式：　请你尝试用文字概括这个结论。 我们可以直接利用它进行计算.如 43×45=43+5=48运算形式运算方法（同底、乘法） （底不变、指相加） 幂的底数必须相同，
相乘时指数才能相加.(4)108 ×105=1013108+5=am · an = am+n(1)23 ×24=a7=27 (2)53×54=57(3)a3 · a4=(a · a · a) (a · a · a · a)=(2 ×2 ×2) ×(2 ×2 ×2 ×2)=(5 × 5 × 5) ×(5 × 5 × 5 × 5)=23+4=53+4=a3+4 例1：计算 (3) a · a3 · a5 = a4 · a5 =a9(1) 103×104 (2) a · a3 (3)a · a3 · a5解：(1) 103×104 =103+4 =107 (2) a · a3 = a 1+3=a4am · an = am+na · a3 · a5 = a4 · a5 =a9想一想： ?当三个或三个以上同底数幂相乘时，是否也 具有这一性质呢？ 怎样用公式表示？如 am·an·ap = am+n+p （m、n、p都是正整数）am · an = am+n1.计算： （1）107 ×104 ；（2）x2 · x5 解：（1）107 ×104 =107 + 4= 1011
（2）x2 · x5 = x2 + 5 = x7 （1）23×24×25 （2）y · y2 · y3 解：（1）23×24×25=23+4+5=212
（2）y · y2 · y3 = y1+2+3=y6 2.计算： 牛刀小试辩一辩
① a · a2＝ a2 　
　 ② a＋a2 ＝ a3
③ a3 · a3＝ a9 　
　 ④ a3＋a3 ＝ a6 (×) (×) (×)判断下列计算是否正确，并简要说明理由：
(×)深入探索----想一想(1) 计 算：(结果写成幂的形式) ① (- 2)4×(- 2)5 = ②( ) 3 ×( ) 2 = ③ (a+b)2 · (a+b)5 = (-2)9(a+b)7 深入探索----想一想(2) ① 32×3m = ② 5m· 5n = ③ x3 · xn+1 = ④y · yn+2 · yn+4 =3m+25m+ny2n+7Xn+4深入探索----算一算23 + 23=2 × 23= 2434 × 27=34 × 33=37 b2· b3+b · b4 =b5 + b5=2b5 计算：(结果写成幂的形式)已知：am=2， an=3.
求am+n =？.解： am+n = am · an
=2 × 3=6 深入探索----议一议效果检测 x4·x6=x24 ( 　) (2) x·x3=x3 ( 　)
(3) x4+x4=x8 (　 ) (4)x2·x2=2x4 (　 )
(5)a2·a3 - a3·a2 = 0 ( 　 )
(6)x3·y5=(xy)8 ( 　 ) (7) x7+x7=x14 ( 　 )
√××××××判断（正确的打“√”，错误的打“×”）根据乘方的意义及同底数幂的乘法填空：
（1） (23 )2 = 23 × 23 =2( )
（2） (am )n = a( ) (m、n为正整数)
　探索思考今天，我们学到了什么？同底数幂的乘法：
am · an = am+n (m、n为正整数)
am · an · ap = am+n+p
( m、n、p为正整数)夜蝌坊市 http://www.eeyke.com/ geg471uip 谢谢!