数学五年级上西师大版2《探索规律》导学案
文档属性
| 名称 | 数学五年级上西师大版2《探索规律》导学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 255.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-01 07:25:44 | ||
图片预览

文档简介
《探索规律》导学案
【学习目标】
1、能通过平移、旋转和轴对称发现图形变化的规律。
2、能运用平移、旋转和轴对称寻找图形变化的规律。
【温故互查】
请同学们以二人小组完成下列内容:
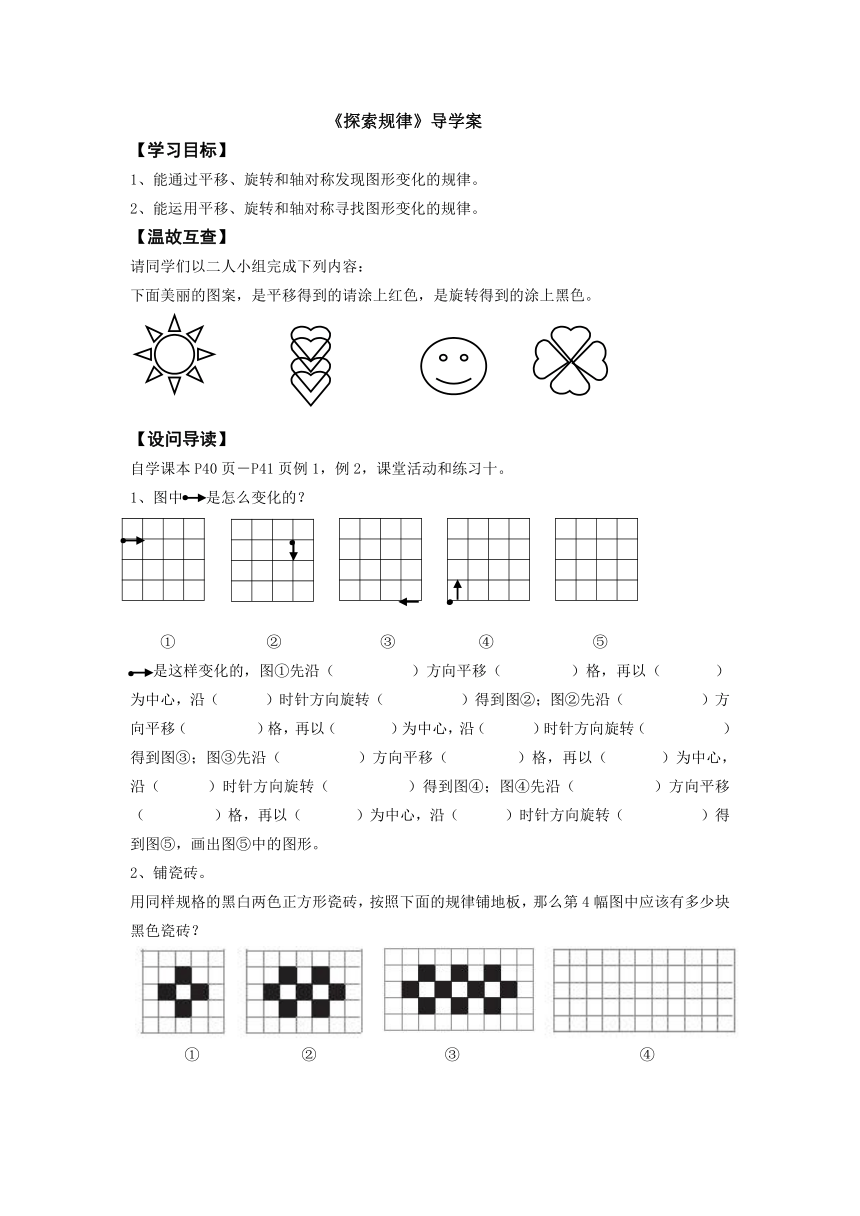
下面美丽的图案,是平移得到的请涂上红色,是旋转得到的涂上黑色。
【设问导读】
自学课本P40页-P41页例1,例2,课堂活动和练习十。
1、图中
是怎么变化的?
①
②
③
④
⑤
是这样变化的,图①先沿(
)方向平移(
)格,再以(
)为中心,沿(
)时针方向旋转(
)得到图②;图②先沿(
)方向平移(
)格,再以(
)为中心,沿(
)时针方向旋转(
)得到图③;图③先沿(
)方向平移(
)格,再以(
)为中心,沿(
)时针方向旋转(
)得到图④;图④先沿(
)方向平移(
)格,再以(
)为中心,沿(
)时针方向旋转(
)得到图⑤,画出图⑤中的图形。
2、铺瓷砖。
用同样规格的黑白两色正方形瓷砖,按照下面的规律铺地板,那么第4幅图中应该有多少块黑色瓷砖?
(1)观察图形。
第1幅图中有4块黑瓷砖,第2幅图中有(
)块黑瓷砖,第3幅图中有(
)块黑瓷砖。
(2)探究排列规律。
我是这样想的:观察可以发现,从第2幅图开始,每一幅图都比前一幅图多(
)块黑瓷砖。因此,第4幅图就有(
)块黑瓷砖。
也可以这样想:第1幅图中的黑瓷砖是(1+3)块,第2幅图中的黑瓷砖是(1+3×2)块,第3幅图中的黑瓷砖是(1+3×3)块,即第4幅图中的黑瓷砖是(1+3×
)块。那么第n幅图中的黑瓷砖是:1+3×(
)或者是4+3×(
)块。
(3)正确解答:第4幅图中应该有(
)块黑瓷砖。
(4)议一议:按这样的规律铺下去,第
10
幅图中有(
)块黑瓷砖。第52幅图中有(
)块黑瓷砖。
【自学检测】
1、画一画,找规律。
我在第1张方格纸上涂
1
格,第2张方格纸上涂2格……
2、
有多少个
。
第8幅图中有(
)个
,第50幅图中有(
)个
。
【巩固练习】
1、前面三幅图形是按一定规律旋转的,画出第四幅图形。
(
)
2、
根据前四幅图的变化规律,完成第5幅。
○
□
◇
△
◇
○
▽
□
△
◇
□
○
□
▽
○
◇
【拓展练习】
从图A
图B
图C
图D是怎样变换的
A
B
C
D
只是(
)发生了变化。
图2可以看作是由图形(
)绕点O按(
)方向,连续旋转了(
)个(
)0,得到的正方形;也可以看作是由图形(
)绕点O按(
)方向,连续旋转了(
)个(
)0,得到的正方形。所以线段OA、OB、OC、OD四条线段的长度是(
);我们还知道图①、图②、图③、图④的面积也是(
),都占正方形面的;如果我们测得线段AB的长度是4cm,那么,三角形AOB的面积是(
)cm2。
四、按要求画图。
以直线MN为对称轴作图A的轴对称图形,得到图形B。
将图形B绕点D顺时针旋转900,得到图形C。
将图形C向左平移6格,得到图形D。
·
·
·
·
·
·
④
③
②
①
图2
【学习目标】
1、能通过平移、旋转和轴对称发现图形变化的规律。
2、能运用平移、旋转和轴对称寻找图形变化的规律。
【温故互查】
请同学们以二人小组完成下列内容:
下面美丽的图案,是平移得到的请涂上红色,是旋转得到的涂上黑色。
【设问导读】
自学课本P40页-P41页例1,例2,课堂活动和练习十。
1、图中
是怎么变化的?
①
②
③
④
⑤
是这样变化的,图①先沿(
)方向平移(
)格,再以(
)为中心,沿(
)时针方向旋转(
)得到图②;图②先沿(
)方向平移(
)格,再以(
)为中心,沿(
)时针方向旋转(
)得到图③;图③先沿(
)方向平移(
)格,再以(
)为中心,沿(
)时针方向旋转(
)得到图④;图④先沿(
)方向平移(
)格,再以(
)为中心,沿(
)时针方向旋转(
)得到图⑤,画出图⑤中的图形。
2、铺瓷砖。
用同样规格的黑白两色正方形瓷砖,按照下面的规律铺地板,那么第4幅图中应该有多少块黑色瓷砖?
(1)观察图形。
第1幅图中有4块黑瓷砖,第2幅图中有(
)块黑瓷砖,第3幅图中有(
)块黑瓷砖。
(2)探究排列规律。
我是这样想的:观察可以发现,从第2幅图开始,每一幅图都比前一幅图多(
)块黑瓷砖。因此,第4幅图就有(
)块黑瓷砖。
也可以这样想:第1幅图中的黑瓷砖是(1+3)块,第2幅图中的黑瓷砖是(1+3×2)块,第3幅图中的黑瓷砖是(1+3×3)块,即第4幅图中的黑瓷砖是(1+3×
)块。那么第n幅图中的黑瓷砖是:1+3×(
)或者是4+3×(
)块。
(3)正确解答:第4幅图中应该有(
)块黑瓷砖。
(4)议一议:按这样的规律铺下去,第
10
幅图中有(
)块黑瓷砖。第52幅图中有(
)块黑瓷砖。
【自学检测】
1、画一画,找规律。
我在第1张方格纸上涂
1
格,第2张方格纸上涂2格……
2、
有多少个
。
第8幅图中有(
)个
,第50幅图中有(
)个
。
【巩固练习】
1、前面三幅图形是按一定规律旋转的,画出第四幅图形。
(
)
2、
根据前四幅图的变化规律,完成第5幅。
○
□
◇
△
◇
○
▽
□
△
◇
□
○
□
▽
○
◇
【拓展练习】
从图A
图B
图C
图D是怎样变换的
A
B
C
D
只是(
)发生了变化。
图2可以看作是由图形(
)绕点O按(
)方向,连续旋转了(
)个(
)0,得到的正方形;也可以看作是由图形(
)绕点O按(
)方向,连续旋转了(
)个(
)0,得到的正方形。所以线段OA、OB、OC、OD四条线段的长度是(
);我们还知道图①、图②、图③、图④的面积也是(
),都占正方形面的;如果我们测得线段AB的长度是4cm,那么,三角形AOB的面积是(
)cm2。
四、按要求画图。
以直线MN为对称轴作图A的轴对称图形,得到图形B。
将图形B绕点D顺时针旋转900,得到图形C。
将图形C向左平移6格,得到图形D。
·
·
·
·
·
·
④
③
②
①
图2
