2017-2018学年冀教版八年级上学期数学期末达标检测卷(含答案)
文档属性
| 名称 | 2017-2018学年冀教版八年级上学期数学期末达标检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 192.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-02 07:07:09 | ||
图片预览



文档简介
八年级上学期数学期末达标检测卷
(120分,90分钟)
题 号
一
二
三
总 分
得 分
一、选择题(每题3分,共48分)
1.要使二次根式有意义,那么x的取值范围是( )
A.x>2 B.x<2 C.x≥2 D.x≤2
2.下列计算正确的是( )
A.+= B.×=6 C.-= D.÷=4
3.若分式的值为0,则x的值是( )
A.2 B.-2 C.±2 D.4
4.-64的立方根与的平方根之和为( )
A.-2或2 B.-2或-6
C.-4+2或-4-2 D.0
5.(中考·德州)下列银行标志中,既不是中心对称图形也不是轴对称图形的是( )
6.若a,b均为正整数,且a>,b<,则a+b的最小值是( )
A.3 B.4 C.5 D.6
7.分式方程=的解是( )
A.x=2 B.x=1 C.x= D.x=-2
8.已知÷M=,则M等于( )
A. B. C. D.
9.下列命题:①两个周长相等的三角形是全等三角形;②两个周长相等的直角三角形是全等三角形;③两个周长相等的等腰三角形是全等三角形;④两个周长相等的等边三角形是全等三角形.其中,真命题有( )【来源:21·世纪·教育·网】
A.1个 B.2个 C.3个 D.4个
10.已知:一等腰三角形的两边长x,y满足方程组则此等腰三角形的周长为( )
A.5 B.4 C.3 D.5或4
11.如图,直角三角板ABC的斜边AB=12 cm,∠A=30°,将三角板ABC绕点C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为( )【来源:21cnj*y.co*m】
A.6 cm B.4 cm
C.(6-2)cm D.(4-6)cm
(第11题)
(第13题)
(第14题)
12.下列性质中,等腰三角形具有而直角三角形不一定具有的是( )
A.两边之和大于第三边 B.有一个角的平分线垂直于这个角的对边
C.有两个锐角的和等于90° D.内角和等于180°
13.(中考·菏泽)如图,数轴上的A,B,C三点所表示的数分别为a,b,c,其中AB=BC,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( )2·1·c·n·j·y
A.点A的左边 B.点A与点B之间
C.点B与点C之间 D.点C的右边
14.如图,△ABC和△DCE都是边长为4的等边三角形,点B,C,E在同一条直线上,则BD的长度为( )21教育名师原创作品
A. B.2 C.3 D.4
15.如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( ) 21*cnjy*com
A. B. C. D.
16.如图,将长方形ABCD对折,得折痕PQ,展开后再沿MN翻折,使点C恰好落在折痕PQ上的点C′处,点D落在D′处,其中M是BC的中点且MN与折痕PQ交于F.连接AC′,BC′,则图中共有等腰三角形的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每题3分,共12分)
17.计算+10的结果为________.
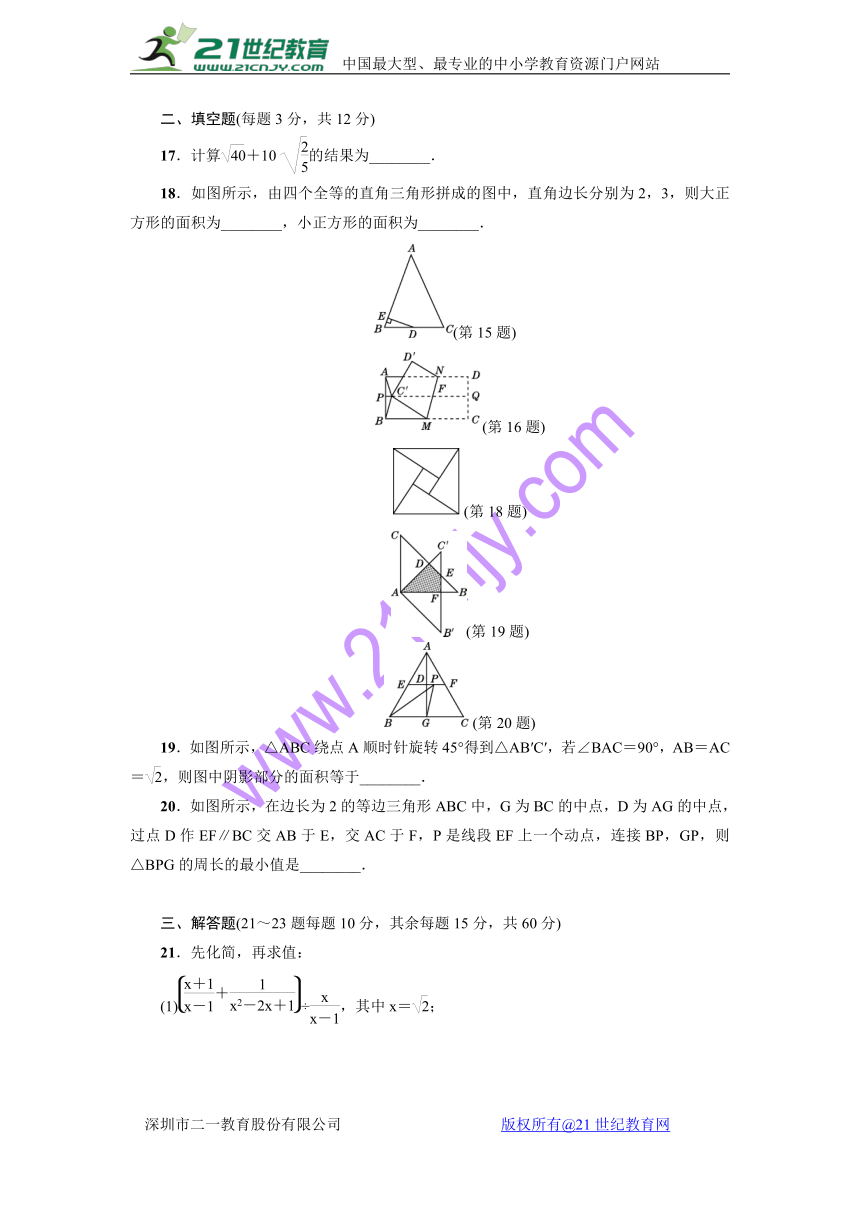
18.如图所示,由四个全等的直角三角形拼成的图中,直角边长分别为2,3,则大正方形的面积为________,小正方形的面积为________.
(第15题)
(第16题)
(第18题)
(第19题)
(第20题)
19.如图所示,△ABC绕点A顺时针旋转45°得到△AB′C′,若∠BAC=90°,AB=AC=,则图中阴影部分的面积等于________.www.21-cn-jy.com
20.如图所示,在边长为2的等边三角形ABC中,G为BC的中点,D为AG的中点,过点D作EF∥BC交AB于E,交AC于F,P是线段EF上一个动点,连接BP,GP,则△BPG的周长的最小值是________.
三、解答题(21~23题每题10分,其余每题15分,共60分)
21.先化简,再求值:
(1)÷,其中x=;
(2)÷+,其中a=+1.
22.(中考·舟山)如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌△DCE;
(2)当∠AEB=50°时,求∠EBC的度数.
(第22题)
23.如图的等边三角形ABC是学校的一块空地,为美化校园,决定把这块空地分为全等的三部分,分别种植不同的花草.现有两种划分方案:(1)分为三个全等的三角形;(2)分为三个全等的四边形.你认为这两种方案能实现吗?若能,画图说明你的划分方法.
(第23题)
24.(中考·烟台)烟台享有“苹果之乡”的美誉.甲、乙两超市分别用3 000元以相同的进价购进质量相同的苹果.甲超市的销售方案是:将苹果按大小分类包装销售,其中大苹果400千克,以进价的2倍销售,剩下的小苹果以高于进价的10%销售.乙超市的销售方案是:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利2 100元(其他成本不计),则:
(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?比较哪种销售方案更合算.
25.课外兴趣小组活动时,老师出示了如下问题:如图①,已知在四边形ABCD中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,求证:AB+AD=AC.
小敏反复探索,不得其解.她想,可先将四边形ABCD特殊化,再进一步解决该问题.
(第25题)
(1)由特殊情况入手,添加条件:“∠B=∠D”,如图②,可证AB+AD=AC.请你完成此证明.
(2)受到(1)的启发,在原问题中,添加辅助线:过C点分别作AB,AD的垂线,垂足分别为点E,F,如图③.请你补全证明过程.21世纪教育网版权所有
答案
一、1.C 解析:本题的易错之处是认为有意义时2x-4>0.
2.C 解析:与的被开方数不同,因此不能合并,A不正确;×==,B不正确;-=2-=,C正确;÷==2,D不正确;故选C.
3.A 解析:本题的易错之处是因为粗心大意,只考虑到分子等于0,而忽略了分母不等于0的限制条件.
4.C 解析:-64的立方根是-4,的平方根是2或-2.本题的易错之处是混淆了“的平方根”与“64的平方根”.21cnjy.com
5.D 解析:选项A:是轴对称图形,也是中心对称图形,故此选项不合题意;
选项B:是轴对称图形,不是中心对称图形,故此选项不合题意;
选项C:是轴对称图形,也是中心对称图形,故此选项不合题意;
选项D:不是轴对称图形,也不是中心对称图形,故此选项符合题意.故选D.
6.B 7.A 8.A 9.A
10.A 解析:本题运用了分类讨论思想,由方程组解得之后,根据组成三角形的条件,经分类讨论可知这个等腰三角形的腰长为2,底边长为1,故周长为2+2+1=5.21教育网
11.C
12.B 解析:A,D是所有三角形都具备的性质;B是等腰三角形具备而直角三角形不一定具备的性质;C是直角三角形具备而等腰三角形不一定具备的性质.
13.C
14.D 解析:因为两个三角形都是边长为4的等边三角形,所以CB=CD,∠CDE=∠DCE=60°,所以∠CDB=∠CBD=30°,在△BDE中,∠BDE=90°,BE=8,DE=4,由勾股定理可得BD=4.21·cn·jy·com
15.C 解析:连接AD,则由已知易得AD⊥BC,在△ABD中根据勾股定理,得AD====12.根据三角形面积公式,可得AB·DE=BD·AD,即13DE=5×12,解得DE=.21·世纪*教育网
16.C 解析:将长方形ABCD对折得折痕PQ,则P,Q分别是AB,CD的中点,且PQ∥AD∥BC,则PQ垂直平分AB,所以AC′=BC′,根据等腰三角形的定义可知△ABC′是等腰三角形.又因为M是BC的中点,折叠后点C落在C′处,则MC=MC′=MB,∠CMF=∠C′MF=∠MFC′,则根据等腰三角形的定义可知△MBC′是等腰三角形,根据等腰三角形的判定定理可知△MFC′是等腰三角形.www-2-1-cnjy-com
二、17.4
18.13;1 解析:根据勾股定理,每个直角三角形的斜边长的平方为22+32=13,即大正方形的面积为13.观察图形可知小正方形的边长为1,则小正方形的面积为1.
19.-1 解析:因为△ABC绕点A顺时针旋转45°得到△AB′C′,∠BAC=90°,AB=AC=,所以BC=2,∠C=∠B=∠CAC′=∠C′=45°.易知AD⊥BC,B′C′⊥AB,可得AD=BC=1,AF=FC′=1,所以S阴影=S△AFC′-S△DEC′=×1×1-×(-1)2=-1.
20.3 解析:由题意得AG⊥BC,点G与点A关于直线EF对称,连接PA,则BP+PG=BP+PA,所以当点A,B,P在一条直线上时,BP+PA的值最小,最小值为2.由题可得BG=1,因为△BPG的周长为BG+PG+BP,所以当BP+PA的值最小时,△BPG的周长最小,最小值是3.2-1-c-n-j-y
三、21.解:(1)÷=·=·=.
当x=时,原式==2+.
(2)÷+=·+=+=.
当a=+1时,原式===.
22.(1)证明:∵∠A=∠D,∠AEB=∠DEC,AB=DC,
∴△ABE≌△DCE.
(2)解:∵△ABE≌△DCE,
∴BE=CE,
∴∠ECB=∠EBC.
∵∠EBC+∠ECB=∠AEB=50°,
∴∠EBC=∠AEB=25°.
23.解:能.划分方法如下:
(1)画△ABC的中线AD,BE,两条中线相交于O点,连接OC,则△ABO,△BCO,△ACO为三个全等的三角形,如图①所示.21*cnjy*com
(2)画△ABC的中线AD,BE,两条中线相交于O点,连接CO并延长交AB于点F,则四边形AEOF,四边形BDOF,四边形CDOE为三个全等的四边形,如图②所示.(答案不唯一)【出处:21教育名师】
(第23题)
24.解:(1)设苹果进价为每千克x元,
根据题意,得
400x+10%x=2 100,解得x=5,经检验,x=5是原方程的根.
故苹果进价为每千克5元.
(2)由(1)知甲、乙两个超市苹果的购进总量都为=600(千克),
乙超市获利600×=1 650(元).
∵2 100>1 650,
甲超市的销售方案更合算.
25.(1)证明:∵∠B=∠D=90°,
AC平分∠DAB,
∠DAB=60°,∴CD=CB,
∠CAB=∠CAD=30°.
设CD=CB=x,则AC=2x.
由勾股定理,得AD=CD=x,AB=CB=x.
∴AD+AB=x+x=2x=AC,即AB+AD=AC.
(2)解:由(1)知,AE+AF=AC.
∵AC为角平分线,CF⊥AD,CE⊥AB,
∴CF=CE,∠CFD=∠CEB=90°.
∵∠ABC与∠D互补,
∠ABC与∠CBE也互补,
∴∠D=∠CBE,
∴△CDF≌△CBE(AAS).
∴DF=BE.∴AB+AD=AB+(AF+FD)=(AB+BE)+AF=AE+AF=AC.
解析:本题运用从特殊到一般的思想求解,即:从特殊图形②中证出AB+AD=AC,然后根据这个解题思路证明一般图形③,通过添加辅助线,实现了由“特殊”到“一般”的转化过程并达到解决问题的目的.【版权所有:21教育】
(120分,90分钟)
题 号
一
二
三
总 分
得 分
一、选择题(每题3分,共48分)
1.要使二次根式有意义,那么x的取值范围是( )
A.x>2 B.x<2 C.x≥2 D.x≤2
2.下列计算正确的是( )
A.+= B.×=6 C.-= D.÷=4
3.若分式的值为0,则x的值是( )
A.2 B.-2 C.±2 D.4
4.-64的立方根与的平方根之和为( )
A.-2或2 B.-2或-6
C.-4+2或-4-2 D.0
5.(中考·德州)下列银行标志中,既不是中心对称图形也不是轴对称图形的是( )
6.若a,b均为正整数,且a>,b<,则a+b的最小值是( )
A.3 B.4 C.5 D.6
7.分式方程=的解是( )
A.x=2 B.x=1 C.x= D.x=-2
8.已知÷M=,则M等于( )
A. B. C. D.
9.下列命题:①两个周长相等的三角形是全等三角形;②两个周长相等的直角三角形是全等三角形;③两个周长相等的等腰三角形是全等三角形;④两个周长相等的等边三角形是全等三角形.其中,真命题有( )【来源:21·世纪·教育·网】
A.1个 B.2个 C.3个 D.4个
10.已知:一等腰三角形的两边长x,y满足方程组则此等腰三角形的周长为( )
A.5 B.4 C.3 D.5或4
11.如图,直角三角板ABC的斜边AB=12 cm,∠A=30°,将三角板ABC绕点C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为( )【来源:21cnj*y.co*m】
A.6 cm B.4 cm
C.(6-2)cm D.(4-6)cm
(第11题)
(第13题)
(第14题)
12.下列性质中,等腰三角形具有而直角三角形不一定具有的是( )
A.两边之和大于第三边 B.有一个角的平分线垂直于这个角的对边
C.有两个锐角的和等于90° D.内角和等于180°
13.(中考·菏泽)如图,数轴上的A,B,C三点所表示的数分别为a,b,c,其中AB=BC,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( )2·1·c·n·j·y
A.点A的左边 B.点A与点B之间
C.点B与点C之间 D.点C的右边
14.如图,△ABC和△DCE都是边长为4的等边三角形,点B,C,E在同一条直线上,则BD的长度为( )21教育名师原创作品
A. B.2 C.3 D.4
15.如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( ) 21*cnjy*com
A. B. C. D.
16.如图,将长方形ABCD对折,得折痕PQ,展开后再沿MN翻折,使点C恰好落在折痕PQ上的点C′处,点D落在D′处,其中M是BC的中点且MN与折痕PQ交于F.连接AC′,BC′,则图中共有等腰三角形的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每题3分,共12分)
17.计算+10的结果为________.
18.如图所示,由四个全等的直角三角形拼成的图中,直角边长分别为2,3,则大正方形的面积为________,小正方形的面积为________.
(第15题)
(第16题)
(第18题)
(第19题)
(第20题)
19.如图所示,△ABC绕点A顺时针旋转45°得到△AB′C′,若∠BAC=90°,AB=AC=,则图中阴影部分的面积等于________.www.21-cn-jy.com
20.如图所示,在边长为2的等边三角形ABC中,G为BC的中点,D为AG的中点,过点D作EF∥BC交AB于E,交AC于F,P是线段EF上一个动点,连接BP,GP,则△BPG的周长的最小值是________.
三、解答题(21~23题每题10分,其余每题15分,共60分)
21.先化简,再求值:
(1)÷,其中x=;
(2)÷+,其中a=+1.
22.(中考·舟山)如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌△DCE;
(2)当∠AEB=50°时,求∠EBC的度数.
(第22题)
23.如图的等边三角形ABC是学校的一块空地,为美化校园,决定把这块空地分为全等的三部分,分别种植不同的花草.现有两种划分方案:(1)分为三个全等的三角形;(2)分为三个全等的四边形.你认为这两种方案能实现吗?若能,画图说明你的划分方法.
(第23题)
24.(中考·烟台)烟台享有“苹果之乡”的美誉.甲、乙两超市分别用3 000元以相同的进价购进质量相同的苹果.甲超市的销售方案是:将苹果按大小分类包装销售,其中大苹果400千克,以进价的2倍销售,剩下的小苹果以高于进价的10%销售.乙超市的销售方案是:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利2 100元(其他成本不计),则:
(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?比较哪种销售方案更合算.
25.课外兴趣小组活动时,老师出示了如下问题:如图①,已知在四边形ABCD中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,求证:AB+AD=AC.
小敏反复探索,不得其解.她想,可先将四边形ABCD特殊化,再进一步解决该问题.
(第25题)
(1)由特殊情况入手,添加条件:“∠B=∠D”,如图②,可证AB+AD=AC.请你完成此证明.
(2)受到(1)的启发,在原问题中,添加辅助线:过C点分别作AB,AD的垂线,垂足分别为点E,F,如图③.请你补全证明过程.21世纪教育网版权所有
答案
一、1.C 解析:本题的易错之处是认为有意义时2x-4>0.
2.C 解析:与的被开方数不同,因此不能合并,A不正确;×==,B不正确;-=2-=,C正确;÷==2,D不正确;故选C.
3.A 解析:本题的易错之处是因为粗心大意,只考虑到分子等于0,而忽略了分母不等于0的限制条件.
4.C 解析:-64的立方根是-4,的平方根是2或-2.本题的易错之处是混淆了“的平方根”与“64的平方根”.21cnjy.com
5.D 解析:选项A:是轴对称图形,也是中心对称图形,故此选项不合题意;
选项B:是轴对称图形,不是中心对称图形,故此选项不合题意;
选项C:是轴对称图形,也是中心对称图形,故此选项不合题意;
选项D:不是轴对称图形,也不是中心对称图形,故此选项符合题意.故选D.
6.B 7.A 8.A 9.A
10.A 解析:本题运用了分类讨论思想,由方程组解得之后,根据组成三角形的条件,经分类讨论可知这个等腰三角形的腰长为2,底边长为1,故周长为2+2+1=5.21教育网
11.C
12.B 解析:A,D是所有三角形都具备的性质;B是等腰三角形具备而直角三角形不一定具备的性质;C是直角三角形具备而等腰三角形不一定具备的性质.
13.C
14.D 解析:因为两个三角形都是边长为4的等边三角形,所以CB=CD,∠CDE=∠DCE=60°,所以∠CDB=∠CBD=30°,在△BDE中,∠BDE=90°,BE=8,DE=4,由勾股定理可得BD=4.21·cn·jy·com
15.C 解析:连接AD,则由已知易得AD⊥BC,在△ABD中根据勾股定理,得AD====12.根据三角形面积公式,可得AB·DE=BD·AD,即13DE=5×12,解得DE=.21·世纪*教育网
16.C 解析:将长方形ABCD对折得折痕PQ,则P,Q分别是AB,CD的中点,且PQ∥AD∥BC,则PQ垂直平分AB,所以AC′=BC′,根据等腰三角形的定义可知△ABC′是等腰三角形.又因为M是BC的中点,折叠后点C落在C′处,则MC=MC′=MB,∠CMF=∠C′MF=∠MFC′,则根据等腰三角形的定义可知△MBC′是等腰三角形,根据等腰三角形的判定定理可知△MFC′是等腰三角形.www-2-1-cnjy-com
二、17.4
18.13;1 解析:根据勾股定理,每个直角三角形的斜边长的平方为22+32=13,即大正方形的面积为13.观察图形可知小正方形的边长为1,则小正方形的面积为1.
19.-1 解析:因为△ABC绕点A顺时针旋转45°得到△AB′C′,∠BAC=90°,AB=AC=,所以BC=2,∠C=∠B=∠CAC′=∠C′=45°.易知AD⊥BC,B′C′⊥AB,可得AD=BC=1,AF=FC′=1,所以S阴影=S△AFC′-S△DEC′=×1×1-×(-1)2=-1.
20.3 解析:由题意得AG⊥BC,点G与点A关于直线EF对称,连接PA,则BP+PG=BP+PA,所以当点A,B,P在一条直线上时,BP+PA的值最小,最小值为2.由题可得BG=1,因为△BPG的周长为BG+PG+BP,所以当BP+PA的值最小时,△BPG的周长最小,最小值是3.2-1-c-n-j-y
三、21.解:(1)÷=·=·=.
当x=时,原式==2+.
(2)÷+=·+=+=.
当a=+1时,原式===.
22.(1)证明:∵∠A=∠D,∠AEB=∠DEC,AB=DC,
∴△ABE≌△DCE.
(2)解:∵△ABE≌△DCE,
∴BE=CE,
∴∠ECB=∠EBC.
∵∠EBC+∠ECB=∠AEB=50°,
∴∠EBC=∠AEB=25°.
23.解:能.划分方法如下:
(1)画△ABC的中线AD,BE,两条中线相交于O点,连接OC,则△ABO,△BCO,△ACO为三个全等的三角形,如图①所示.21*cnjy*com
(2)画△ABC的中线AD,BE,两条中线相交于O点,连接CO并延长交AB于点F,则四边形AEOF,四边形BDOF,四边形CDOE为三个全等的四边形,如图②所示.(答案不唯一)【出处:21教育名师】
(第23题)
24.解:(1)设苹果进价为每千克x元,
根据题意,得
400x+10%x=2 100,解得x=5,经检验,x=5是原方程的根.
故苹果进价为每千克5元.
(2)由(1)知甲、乙两个超市苹果的购进总量都为=600(千克),
乙超市获利600×=1 650(元).
∵2 100>1 650,
甲超市的销售方案更合算.
25.(1)证明:∵∠B=∠D=90°,
AC平分∠DAB,
∠DAB=60°,∴CD=CB,
∠CAB=∠CAD=30°.
设CD=CB=x,则AC=2x.
由勾股定理,得AD=CD=x,AB=CB=x.
∴AD+AB=x+x=2x=AC,即AB+AD=AC.
(2)解:由(1)知,AE+AF=AC.
∵AC为角平分线,CF⊥AD,CE⊥AB,
∴CF=CE,∠CFD=∠CEB=90°.
∵∠ABC与∠D互补,
∠ABC与∠CBE也互补,
∴∠D=∠CBE,
∴△CDF≌△CBE(AAS).
∴DF=BE.∴AB+AD=AB+(AF+FD)=(AB+BE)+AF=AE+AF=AC.
解析:本题运用从特殊到一般的思想求解,即:从特殊图形②中证出AB+AD=AC,然后根据这个解题思路证明一般图形③,通过添加辅助线,实现了由“特殊”到“一般”的转化过程并达到解决问题的目的.【版权所有:21教育】
同课章节目录
