陕西省黄陵中学2016-2017学年高二(重点班)下学期第四学月考试数学(理)试题 Word版含答案
文档属性
| 名称 | 陕西省黄陵中学2016-2017学年高二(重点班)下学期第四学月考试数学(理)试题 Word版含答案 | 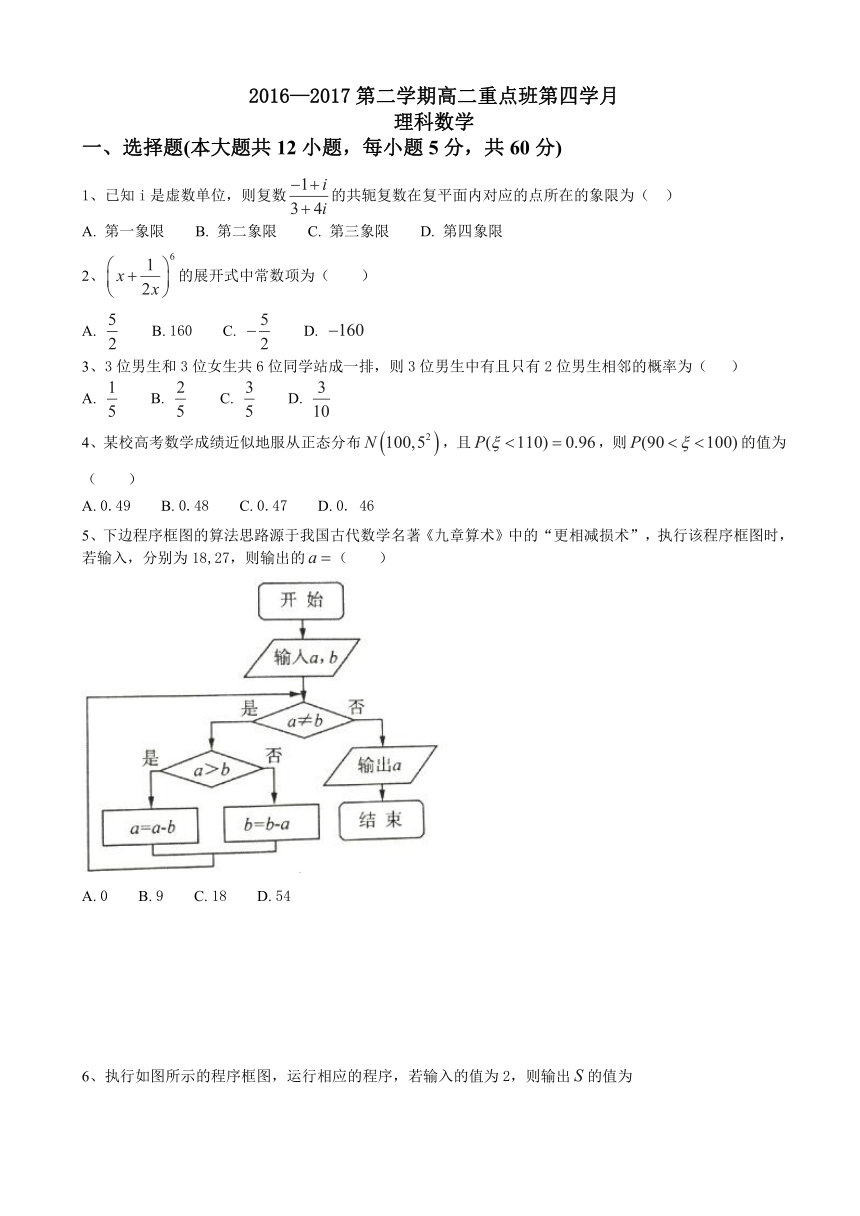 | |
| 格式 | zip | ||
| 文件大小 | 325.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-05 21:54:08 | ||
图片预览



文档简介
2016—2017第二学期高二重点班第四学月
理科数学
一、选择题(本大题共12小题,每小题5分,共60分)
1、已知i是虚数单位,则复数的共轭复数在复平面内对应的点所在的象限为( )
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
2、的展开式中常数项为(
)
A.
B.
160
C.
D.
3、3位男生和3位女生共6位同学站成一排,则3位男生中有且只有2位男生相邻的概率为(
)
A.
B.
C.
D.
4、某校高考数学成绩近似地服从正态分布,且,则的值为(
)
A.
0.49
B.
0.48
C.
0.47
D.
0.
46
5、下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图时,若输入,分别为18,27,则输出的(
)
A.
0
B.
9
C.
18
D.
54
6、执行如图所示的程序框图,运行相应的程序,若输入的值为2,则输出的值为
A.
64
B.
84
C.
340
D.
1364
7、将两枚质地均匀的骰子各掷一次,设事件A={两个点数互不相同},B={出现一个5点},则P(B|A)=( )
A.
B.
C.
D.
8、若实数a=2-,则a10-2Ca9+22Ca8-…+210等于( )
A.32
B.-32
C.1
024
D.512
9、4名大学生到三家企业应聘,每名大学生至多被一家企业录用,则每家企业至少录用一名大学生的情况有( )
A.24种
B.36种
C.48种
D.60种
10、下列说法中正确的是( )
A.相关关系是一种不确定的关系,回归分析是对相关关系的分析,因此没有实际意义
B.独立性检验对分类变量关系的研究没有100%的把握,所以独立性检验研究的结果在实际中也没有多大的实际意义
C.相关关系可以对变量的发展趋势进行预报,这种预报可能会是错误的
D.独立性检验如果得出的结论有99%的可信度,就意味着这个结论一定是正确的
11、如图,
5个(x,y)数据,去掉D(3,10)后,下列说法错误的是( )
INCLUDEPICTURE
"../../../"
\
MERGEFORMAT
A.相关系数r变大
B.残差平方和变大
C.R2变大
D.解释变量x与预报变量y的相关性变强
12、一射手对靶射击,直到第一次命中为止,每次命中的概率为0.6,现有4颗子弹,命中后的剩余子弹数目
ξ的期望为( )
A.2.44
B.3.376
C.2.376
D.2.4
二、填空题(本大题共4小题,每小题5分,共20分)
13、设
z
∈C
,
满足2<|z|<4.条件的点
z
的集合是
;
14、设复数满足条件则z=
;
15、平面上,点、为射线上的两点,点、为射线上的两点,则有(其中、分别为、的面积);空间中,点、为射线上的两点,点、为射线上的两点,点、为射线上的两点,则有______(其中、分别为四面体、的体积).
16、袋中有4只红球3只黑球,从袋中任取4只球,取到1只红球得1分,取到1只黑球得3分,设得分为随机变量X,则P(X≤6)=
.
三、解答题(本大题共4小题,共40分)
17、(本小题满分10分)的展开式中的系数是20,求实数a的值.
18、(本小题满分10分)某种药种植基地有两处种植区的药材需在下周一、周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘,由于下雨会影响药材的收益,若基地收益如下表所示:已知下周一和下周二无雨的概率相同且为,两天是否下雨互不影响,若两天都下雨的概率为
(1)求及基地的预期收益;
(2)若该基地额外聘请工人,可在周一当天完成全部采摘任务,若周一无雨时收益为万元,有雨时收益为6万元,且额外聘请工人的成本为元,问该基地是否应该额外聘请工人,请说明理由.
19、(本小题满分10分)
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,给当地人民造成了巨大的财产损失,适逢暑假,小张调查了当地某小区的100户居民由于台风造成的经济损失,将收集的数据分成,,,,五组,并作出如下频率分布直方图(图1):
(Ⅰ)台风后居委会号召小区居民为台风重灾区捐款,小张调查的100户居民捐款情况如右下表格,在图2表格空白处填写正确数字,并说明是否有以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
(Ⅱ)将上述调查所得到的频率视为概率.
现在从该地区大量受灾居民中,采用随机抽样方法每次抽取1户居民,抽取3次,记被抽取的3户居民中自身经济损失超过4000元的人数为.
若每次抽取的结果是相互独立的,求的分布列,期望和方差.
经济损失不超过4000元
经济损失超过4000元
合计
捐款超过500元
60
捐款不超过500元
10
合计
附:临界值表
0.10
0.05
0.025
2.706
3.841
5.024
随机量变
20、在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列{n∈N+}.
求a2,a3,a4及b2,b3,b4,由此猜测{an},{bn}的通项公式,并证明你的结论;
答案
选择题
1、D;2、A;3、C;4、D;5、B;6、B;7、A;8、A;9、D;10、C;11、B;12、C。
二、填空题
13、圆环;14、;15、;16、。
17
、
18、
19、
(Ⅰ)由频率分布直方图可知,在抽取的100人中,经济损失不超过4000元的有70人,经济损失超过4000元的有30人,则表格数据如下
经济损失不超过4000元
经济损失超过4000元
合计
捐款超过500元
60
20
80
捐款不超过500元
10
10
20
合计
70
30
100
………………2分
.
因为,.
所以有以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关.
………………………………………………………………………4分
(Ⅱ)由频率分布直方图可知抽到自身经济损失超过4000元居民的频率为0.3,将频率视为概率.
由题意知的取值可能有,………………………………………………5分
,
,……………………………………6分
,……………………………………7分
,……………………………………8分
,……………………………………9分
从而的分布列为
………………………10分
,……………………………………………11分
………………………………12分
20、
[规范解答]
由条件得2bn=an+an+1,
a=bnbn+1.
由此可以得a2=6,b2=9,a3=12,b3=16,a4=20,b4=25.
猜测an=n(n+1),bn=(n+1)2.(5分)
用数学归纳法证明:
①当n=1时,由上可得结论成立.
②假设当n=k(k∈N
)时,结论成立.
即ak=k(k+1),bk=(k+1)2,
那么当n=k+1时,
ak+1=2bk-ak=2(k+1)2-k(k+1)
=(k+1)(k+2),bk+1==(k+2)2,
所以当n=k+1时,结论也成立.
由①②,可知an=n(n+1),
bn=(n+1)2对一切正整数都成立.(10分)
(图1)
(图2)
理科数学
一、选择题(本大题共12小题,每小题5分,共60分)
1、已知i是虚数单位,则复数的共轭复数在复平面内对应的点所在的象限为( )
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
2、的展开式中常数项为(
)
A.
B.
160
C.
D.
3、3位男生和3位女生共6位同学站成一排,则3位男生中有且只有2位男生相邻的概率为(
)
A.
B.
C.
D.
4、某校高考数学成绩近似地服从正态分布,且,则的值为(
)
A.
0.49
B.
0.48
C.
0.47
D.
0.
46
5、下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图时,若输入,分别为18,27,则输出的(
)
A.
0
B.
9
C.
18
D.
54
6、执行如图所示的程序框图,运行相应的程序,若输入的值为2,则输出的值为
A.
64
B.
84
C.
340
D.
1364
7、将两枚质地均匀的骰子各掷一次,设事件A={两个点数互不相同},B={出现一个5点},则P(B|A)=( )
A.
B.
C.
D.
8、若实数a=2-,则a10-2Ca9+22Ca8-…+210等于( )
A.32
B.-32
C.1
024
D.512
9、4名大学生到三家企业应聘,每名大学生至多被一家企业录用,则每家企业至少录用一名大学生的情况有( )
A.24种
B.36种
C.48种
D.60种
10、下列说法中正确的是( )
A.相关关系是一种不确定的关系,回归分析是对相关关系的分析,因此没有实际意义
B.独立性检验对分类变量关系的研究没有100%的把握,所以独立性检验研究的结果在实际中也没有多大的实际意义
C.相关关系可以对变量的发展趋势进行预报,这种预报可能会是错误的
D.独立性检验如果得出的结论有99%的可信度,就意味着这个结论一定是正确的
11、如图,
5个(x,y)数据,去掉D(3,10)后,下列说法错误的是( )
INCLUDEPICTURE
"../../../"
\
MERGEFORMAT
A.相关系数r变大
B.残差平方和变大
C.R2变大
D.解释变量x与预报变量y的相关性变强
12、一射手对靶射击,直到第一次命中为止,每次命中的概率为0.6,现有4颗子弹,命中后的剩余子弹数目
ξ的期望为( )
A.2.44
B.3.376
C.2.376
D.2.4
二、填空题(本大题共4小题,每小题5分,共20分)
13、设
z
∈C
,
满足2<|z|<4.条件的点
z
的集合是
;
14、设复数满足条件则z=
;
15、平面上,点、为射线上的两点,点、为射线上的两点,则有(其中、分别为、的面积);空间中,点、为射线上的两点,点、为射线上的两点,点、为射线上的两点,则有______(其中、分别为四面体、的体积).
16、袋中有4只红球3只黑球,从袋中任取4只球,取到1只红球得1分,取到1只黑球得3分,设得分为随机变量X,则P(X≤6)=
.
三、解答题(本大题共4小题,共40分)
17、(本小题满分10分)的展开式中的系数是20,求实数a的值.
18、(本小题满分10分)某种药种植基地有两处种植区的药材需在下周一、周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘,由于下雨会影响药材的收益,若基地收益如下表所示:已知下周一和下周二无雨的概率相同且为,两天是否下雨互不影响,若两天都下雨的概率为
(1)求及基地的预期收益;
(2)若该基地额外聘请工人,可在周一当天完成全部采摘任务,若周一无雨时收益为万元,有雨时收益为6万元,且额外聘请工人的成本为元,问该基地是否应该额外聘请工人,请说明理由.
19、(本小题满分10分)
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,给当地人民造成了巨大的财产损失,适逢暑假,小张调查了当地某小区的100户居民由于台风造成的经济损失,将收集的数据分成,,,,五组,并作出如下频率分布直方图(图1):
(Ⅰ)台风后居委会号召小区居民为台风重灾区捐款,小张调查的100户居民捐款情况如右下表格,在图2表格空白处填写正确数字,并说明是否有以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
(Ⅱ)将上述调查所得到的频率视为概率.
现在从该地区大量受灾居民中,采用随机抽样方法每次抽取1户居民,抽取3次,记被抽取的3户居民中自身经济损失超过4000元的人数为.
若每次抽取的结果是相互独立的,求的分布列,期望和方差.
经济损失不超过4000元
经济损失超过4000元
合计
捐款超过500元
60
捐款不超过500元
10
合计
附:临界值表
0.10
0.05
0.025
2.706
3.841
5.024
随机量变
20、在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列{n∈N+}.
求a2,a3,a4及b2,b3,b4,由此猜测{an},{bn}的通项公式,并证明你的结论;
答案
选择题
1、D;2、A;3、C;4、D;5、B;6、B;7、A;8、A;9、D;10、C;11、B;12、C。
二、填空题
13、圆环;14、;15、;16、。
17
、
18、
19、
(Ⅰ)由频率分布直方图可知,在抽取的100人中,经济损失不超过4000元的有70人,经济损失超过4000元的有30人,则表格数据如下
经济损失不超过4000元
经济损失超过4000元
合计
捐款超过500元
60
20
80
捐款不超过500元
10
10
20
合计
70
30
100
………………2分
.
因为,.
所以有以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关.
………………………………………………………………………4分
(Ⅱ)由频率分布直方图可知抽到自身经济损失超过4000元居民的频率为0.3,将频率视为概率.
由题意知的取值可能有,………………………………………………5分
,
,……………………………………6分
,……………………………………7分
,……………………………………8分
,……………………………………9分
从而的分布列为
………………………10分
,……………………………………………11分
………………………………12分
20、
[规范解答]
由条件得2bn=an+an+1,
a=bnbn+1.
由此可以得a2=6,b2=9,a3=12,b3=16,a4=20,b4=25.
猜测an=n(n+1),bn=(n+1)2.(5分)
用数学归纳法证明:
①当n=1时,由上可得结论成立.
②假设当n=k(k∈N
)时,结论成立.
即ak=k(k+1),bk=(k+1)2,
那么当n=k+1时,
ak+1=2bk-ak=2(k+1)2-k(k+1)
=(k+1)(k+2),bk+1==(k+2)2,
所以当n=k+1时,结论也成立.
由①②,可知an=n(n+1),
bn=(n+1)2对一切正整数都成立.(10分)
(图1)
(图2)
同课章节目录
