2017-2018学年高二物理新人教版选修3-2基础训练:第4章 4 法拉第电磁感应定律
文档属性
| 名称 | 2017-2018学年高二物理新人教版选修3-2基础训练:第4章 4 法拉第电磁感应定律 | 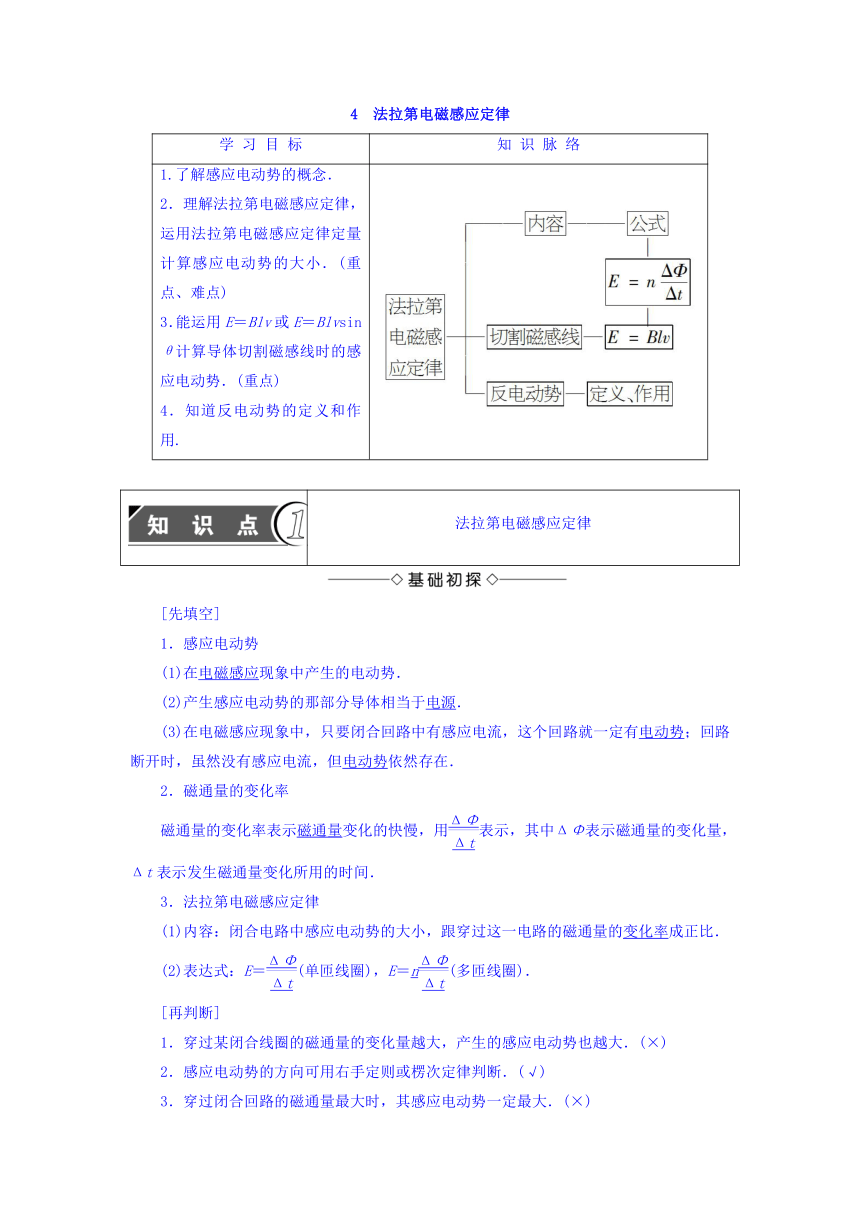 | |
| 格式 | zip | ||
| 文件大小 | 268.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2017-07-05 11:32:37 | ||
图片预览





文档简介
4 法拉第电磁感应定律
学
习
目
标
知
识
脉
络
1.了解感应电动势的概念.2.理解法拉第电磁感应定律,运用法拉第电磁感应定律定量计算感应电动势的大小.(重点、难点)3.能运用E=Blv或E=Blvsin
θ计算导体切割磁感线时的感应电动势.(重点)4.知道反电动势的定义和作用.
法拉第电磁感应定律
1.感应电动势
(1)在电磁感应现象中产生的电动势.
(2)产生感应电动势的那部分导体相当于电源.
(3)在电磁感应现象中,只要闭合回路中有感应电流,这个回路就一定有电动势;回路断开时,虽然没有感应电流,但电动势依然存在.
2.磁通量的变化率
磁通量的变化率表示磁通量变化的快慢,用表示,其中ΔΦ表示磁通量的变化量,Δt表示发生磁通量变化所用的时间.
3.法拉第电磁感应定律
(1)内容:闭合电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比.
(2)表达式:E=(单匝线圈),E=n(多匝线圈).
1.穿过某闭合线圈的磁通量的变化量越大,产生的感应电动势也越大.(×)
2.感应电动势的方向可用右手定则或楞次定律判断.(√)
3.穿过闭合回路的磁通量最大时,其感应电动势一定最大.(×)
产生感应电动势的条件是什么?
【提示】 不管电路是否闭合,只要穿过电路的磁通量发生变化,电路中就会产生感应电动势.
如图4 4 1所示,将一条形磁铁插入线圈中时,电流表的指针要发生偏转.
图4 4 1
探讨1:若将磁铁分别快速和缓慢插入线圈中时,磁通量的变化量及变化率是否相同.
【提示】 两种情况下磁通量的变化量ΔΦ相同,磁通量的变化率不同,所用时间Δt越少,变化率越大,反之变化率越小.
探讨2:将磁铁快速和缓慢插入线圈中时,电流表的指针偏转角度是否相同?为什么?
【提示】 两种情况下电流表的指针偏转角度不同,快速插入时电流表指针偏转角度大,缓慢插入时电流表指针偏转角度小.电路中电流的大小I=,又E=n,即I∝,所以快速插入时电路中的电流大.
1.感应电动势的相关因素
(1)感应电动势E的大小取决于穿过电路的磁通量变化率和匝数n,而与Φ的大小、ΔΦ的大小没有必然的关系;
(2)感应电动势E的大小与电路的电阻R也无关,但感应电流的大小与E及回路总电阻R都有关.
2.磁通量的变化率在Φ
t图象上是某点切线的斜率.
3.感应电动势E=n的两种基本形式:
(1)当垂直于磁场方向的线圈面积S不变,磁感应强度B发生变化时,ΔΦ=ΔB·S,则E=nS,其中叫磁感应强度B的变化率.
(2)当磁感应强度B不变,垂直于磁场方向的线圈面积S发生变化时,ΔΦ=B·ΔS,则E=nB.
4.E=n求出的是Δt时间内的平均感应电动势.
5.Φ、ΔΦ与三者之间的关系.
物理量
单位
物理意义
计算公式
磁通量Φ
Wb
表示某时刻或某位置时穿过某一面积的磁感线条数的多少
Φ=B·S⊥
磁通量的变化量ΔΦ
Wb
表示在某一过程中穿过某一面积的磁通量变化的多少
ΔΦ=|Φ2-Φ1|
磁通量的变化率
Wb/s
表示穿过某一面积的磁通量变化的快慢
=
1.穿过某闭合回路的磁通量Φ随时间t变化的图象分别如图4 4 2中的①~④所示,下列说法正确的是( )
图4 4 2
A.图①有感应电动势,且大小恒定不变
B.图②产生的感应电动势一直在变大
C.图③在0~t1内的感应电动势大小是在t1~t2内的2倍
D.图④产生的感应电动势先变大再变小
【解析】 感应电动势E=n,而对应Φ t图象中图线切线斜率的绝对值,根据图线切线斜率的变化情况可得①中无感应电动势,②中感应电动势恒定不变,③中感应电动势在0~t1内的大小是在t1~t2内大小的2倍,④中感应电动势先变小再变大,选项C正确.
【答案】 C
2.穿过一个内阻为1
Ω的10匝闭合线圈的磁通量每秒均匀减少2
Wb,则线圈中( )
A.感应电动势每秒增加2
V
B.感应电动势每秒减少2
V
C.磁通量的变化率为2
Wb/s
D.感应电流为2
A
【解析】 磁通量的变化率=2
Wb/s,C正确.由E=n得E=10×2
V=20
V,感应电动势不变,A、B错误.由I=得I=
A=20
A,D错误.
【答案】 C
3.如图4 4 3甲所示,在竖直向上的匀强磁场中,水平放置一个不变形的单匝金属圆线圈,规定线圈中感应电流的正方向如图所示.当磁场的磁感应强度B随时间t做如图乙所示的变化时,图中能正确表示线圈中感应电动势E变化的是( )
甲 乙
图4 4 3
【解析】 由法拉第电磁感应定律,E=n=n,在0~1
s内,B均匀增大,则为一恒量,则E为一恒量,再由楞次定律,可判断感应电动势为顺时针方向,则电动势为正值;在1~3
s内,B不变化,则感应电动势为零;在3~5
s内,B均匀减小,则为一恒量,但B变化得较慢,则E为一恒量,但比前者小,再由楞次定律,可判断感应电动势为逆时针方向,则电动势为负值,所以A选项正确.
【答案】 A
4.一个200匝、面积为20
cm2的线圈,放在磁场中,磁场的方向与线圈平面成30°角,若磁感应强度在0.05
s内由0.1
T
增加到0.5
T,在此过程中磁通量变化了多少?磁通量的平均变化率是多少?线圈中感应电动势的大小是多少?
【解析】 磁通量的变化是由磁场的变化引起的,应该用公式ΔΦ=ΔBSsin
θ来计算,
所以ΔΦ=ΔBSsin
θ=(0.5-0.1)×20×10-4×0.5
Wb=4×10-4
Wb
磁通量的平均变化率
=Wb/s=8×10-3Wb/s
感应电动势的大小可根据法拉第电磁感应定律计算E=n=200×8×10-3V=1.6
V.
【答案】 4×10-4Wb 8×10-3Wb/s 1.6
V
5.如图4 4 4所示,面积为0.2
m2的100匝线圈处在匀强磁场中,磁场方向垂直于线圈平面,已知磁感应强度随时间变化的规律为B=(2+0.2t)T,定值电阻R1=6
Ω,线圈电阻R2=4
Ω,求:
图4 4 4
(1)回路的感应电动势;
(2)流过R1的电流;
(3)a、b两点间电压Uab.
【解析】 (1)=0.2
T/s
E==n·S=100×0.04
V=4
V.
(2)等效电路如图.
根据闭合电路欧姆定律有I==0.4
A.
(3)a、b两点间的电压Uab=IR1=2.4
V.
【答案】 (1)4
V (2)0.4
A (3)2.4
V
计算磁通量ΔΦ的三种方法
1.若磁通量的变化是由回路包围的面积引起的,ΔΦ=B·ΔS.
2.若磁通量的变化是由磁场变化引起的,ΔΦ=ΔB·S.
3.若磁通量的变化是由面积和磁感应强度方向变化引起的,ΔΦ=Φ2-Φ1.
导线切割磁感线产生的感应电动势,反电动势
1.磁场方向、导体棒与导体棒运动方向三者两两垂直时:E=Blv.
2.如图4 4 5所示,导体棒与磁场方向垂直,导体棒的运动方向与导体棒本身垂直,但与磁场方向夹角为θ时,E=Blvsin
θ.
图4 4 5
3.反电动势
(1)定义:电动机转动时,由于切割磁感线,线圈中产生的削弱电源电动势作用的电动势.
(2)作用:阻碍线圈的转动.
1.对于E=Blv中的B、l、v三者必须相互垂直.(√)
2.导体棒在磁场中运动速度越大,产生的感应电动势一定越大.(×)
3.当B、l、v三者大小、方向均不变时,在Δt时间内的平均感应电动势和它在任意时刻产生的瞬时感应电动势相同.(√)
4.电动机通电转动,电动机中出现的感应电动势为反电动势,反电动势会阻碍线圈的运动.(√)
5.电动机正常工作时,反电动势会加快线圈的运动.(×)
6.电动机工作中由于机械阻力过大而停止转动,就没有了反电动势,线圈中的电流会很大,很容易烧毁电动机.(√)
1.如图4 4 6所示,一边长为L的正方形导线框abcd垂直于磁感线,以速度v在匀强磁场中向右运动,甲同学说:由法拉第电磁感应定律可知,这时穿过线框的磁通量的变化率为零,所以线框中感应电动势应该为零.乙同学说线框中ad和bc边均以速度v做切割磁感线运动,由E=BLv可知,这两条边都应该产生电动势且Ead=Ebc=BLv.他们各执一词,到底谁说的对呢?
图4 4 6
【提示】 这两个同学说的并不矛盾,虽然ad边与bc边都产生感应电动势,但由于方向相反,相当于两个电源并联没有对外供电,所以整个回路的电动势为零.可见,用法拉第电磁感应定律求出的是整个回路的感应电动势,而用E=BLv求的是回路中做切割磁感线的那部分导体产生的电动势.
2.电动机工作时,加在电动机上的电压U和流经电动机的电流I及电动机线圈电阻r三者之间是否满足I=?
【提示】 电动机转动时其线圈中要产生一个反电动势U′,加在线圈电阻上的电压Ur远小于U,所以I=不成立.此时线圈中的电流I=.
如图4 4 7所示,一个半径为r的半圆形导体,处在磁感应强度为B的匀强磁场中.
图4 4 7
探讨1:当导体沿OP方向以速度v做匀速运动时,其感应电动势的大小是多少?
【提示】 导线的有效长度l=2r,则感应电动势E=Blv=2Brv.
探讨2:当导体沿MN方向以速度v做匀速运动时,其感应电动势的大小是多少?
【提示】 此时导线的有效长度l=r,则感应电动势E=Blv=Brv.
1.对公式E=Blvsin
θ的理解
(1)若导线垂直切割磁感线时,即B、l、v三者两两垂直,公式中θ=90°,此时E=Blv,感应电动势最大,此式常用来计算瞬时感应电动势.
(2)导线不垂直切割磁感线时,即v与B有一夹角θ时,如图4 4 8所示,此时可将导线的速度v向垂直于磁感线和平行于磁感线两个方向分解,则分速度v2=vcos
θ不使导线切割磁感线,使导线切割磁感线的是分速度v1=vsin
θ,从而使导线产生的感应电动势为E=Blv1=Blvsin
θ.
图4 4 8
(3)若导线是曲折的,则l应是导线的有效切割长度,即导线两端点在v、B所决定平面的垂线上的长度.如图4 4 9甲所示的三种情况下感应电动势相同;如图乙所示的半径为r的圆弧形导体垂直切割磁感线时,感应电动势E=Blv≠2Brv.
甲 乙
图4 4 9
2.公式E=n与E=Blvsin
θ的区别与联系
E=n
E=Blvsin
θ
区别
研究对象
某个回路
回路中做切割磁感线运动的那部分导体
研究内容
(1)求的是Δt时间内的平均感应电动势,E与某段时间或某个过程对应(2)当Δt→0时,E为瞬时感应电动势
(1)若v为瞬时速度,公式求的是瞬时感应电动势(2)若v为平均速度,公式求的是平均感应电动势(3)当B、l、v三者均不变时,平均感应电动势与瞬时感应电动势相等
适用范围
对任何电路普遍适用
只适用于导体切割磁感线运动的情况
联系
(1)E=Blvsin
θ可由E=n在一定条件下推导出来(2)整个回路的感应电动势为零时,回路中某段导体的感应电动势不一定为零
3.导体棒转动切割磁感线时的感应电动势
如图4 4 10所示,长为l的导体棒ab以a为圆心,以角速度ω在磁感应强度为B的匀强磁场中匀速转动,其感应电动势可从两个角度推导.
图4 4 10
(1)棒上各点速度不同,其平均速度=ωl,由E=Blv得棒上感应电动势大小为E=Bl·ωl=Bl2ω.
(2)若经时间Δt,棒扫过的面积为ΔS=πl2=l2ωΔt,磁通量的变化量ΔΦ=B·ΔS=Bl2ωΔt,由E=得棒上感应电动势大小为E=Bl2ω.
6.如图4 4 11所示,MN、PQ为两条平行的水平放置的金属导轨,左端接有定值电阻R,金属棒ab斜放在两导轨之间,与导轨接触良好,ab=L.磁感应强度为B的匀强磁场垂直于导轨平面,设金属棒与两导轨间夹角为60°,以速度v水平向右匀速运动,不计导轨和棒的电阻,则流过金属棒中的电流为( )
图4 4 11
A.I=
B.I=
C.I=
D.I=
【解析】 导体棒切割磁感线的有效长度为:L·sin
60°=L,故感应电动势E=Bv,由闭合电路欧姆定律得I=,故选项B正确.
【答案】 B
7.如图4 4 12是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为r,匀强磁场的磁感应强度为B,回路总电阻为R,匀速转动铜盘的角速度为ω.则电路的功率是( )
图4 4 12
A.
B.
C.
D.
【解析】 根据导体棒旋转切割产生电动势E=Bωr2,由P=,得电路的功率是,故选项C正确.
【答案】 C
8.在范围足够大,磁感应强度B=0.2
T,方向竖直向下的匀强磁场中,有一水平放置的光滑框架,宽度l=0.4
m,如图4 4 13所示,框架上放置一质量为0.05
kg、电阻为1
Ω的金属杆cd,框架电阻不计.若金属杆cd以恒定的加速度a=2
m/s2由静止开始水平向右做匀变速运动,求:
图4 4 13
(1)前5
s内平均感应电动势的大小;
(2)第5
s末,回路中电流的大小.
【解析】 (1)前5
s内的位移x=at2=25
m
前5
s内的平均速度==5
m/s
故平均感应电动势的大小E=Bl=0.4
V.
(2)第5
s末速度v′=at=10
m/s
此时感应电动势E′=Blv′
则回路中电流的大小I===0.8
A.
【答案】 (1)0.4
V (2)0.8
A
9.如图4 4 14所示,在磁感应强度为0.2
T的匀强磁场中,有一长为0.5
m、电阻为1.0
Ω的导体AB在金属框架上以10
m/s的速度向右滑动,R1=R2=2.0
Ω,其他电阻不计,求流过R1的电流I1.
图4 4 14
【解析】 AB切割磁感线相当于电源,其等效电路如图所示,
E=Blv=0.2×0.5×10
V=1
V
由闭合电路欧姆定律得I=,R1、R2并联,由并联电路电阻关系得=+
解得:R==1.0
Ω
所以IAB=I=0.5
A
因为R1=R2,所以流过R1的电流为I1==0.25
A.
【答案】 0.25
A
电磁感应中电路问题的分析方法
1.明确哪部分导体或电路产生感应电动势,该导体或电路就是电源,其他部分是外电路.
2.用法拉第电磁感应定律或切割公式确定感应电动势的大小,用楞次定律或右手定则确定感应电动势的方向.
3.分清内外电路,画出等效电路图.
4.运用闭合电路欧姆定律、串并联电路特点、电功率、电热等公式联立求解.
学
习
目
标
知
识
脉
络
1.了解感应电动势的概念.2.理解法拉第电磁感应定律,运用法拉第电磁感应定律定量计算感应电动势的大小.(重点、难点)3.能运用E=Blv或E=Blvsin
θ计算导体切割磁感线时的感应电动势.(重点)4.知道反电动势的定义和作用.
法拉第电磁感应定律
1.感应电动势
(1)在电磁感应现象中产生的电动势.
(2)产生感应电动势的那部分导体相当于电源.
(3)在电磁感应现象中,只要闭合回路中有感应电流,这个回路就一定有电动势;回路断开时,虽然没有感应电流,但电动势依然存在.
2.磁通量的变化率
磁通量的变化率表示磁通量变化的快慢,用表示,其中ΔΦ表示磁通量的变化量,Δt表示发生磁通量变化所用的时间.
3.法拉第电磁感应定律
(1)内容:闭合电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比.
(2)表达式:E=(单匝线圈),E=n(多匝线圈).
1.穿过某闭合线圈的磁通量的变化量越大,产生的感应电动势也越大.(×)
2.感应电动势的方向可用右手定则或楞次定律判断.(√)
3.穿过闭合回路的磁通量最大时,其感应电动势一定最大.(×)
产生感应电动势的条件是什么?
【提示】 不管电路是否闭合,只要穿过电路的磁通量发生变化,电路中就会产生感应电动势.
如图4 4 1所示,将一条形磁铁插入线圈中时,电流表的指针要发生偏转.
图4 4 1
探讨1:若将磁铁分别快速和缓慢插入线圈中时,磁通量的变化量及变化率是否相同.
【提示】 两种情况下磁通量的变化量ΔΦ相同,磁通量的变化率不同,所用时间Δt越少,变化率越大,反之变化率越小.
探讨2:将磁铁快速和缓慢插入线圈中时,电流表的指针偏转角度是否相同?为什么?
【提示】 两种情况下电流表的指针偏转角度不同,快速插入时电流表指针偏转角度大,缓慢插入时电流表指针偏转角度小.电路中电流的大小I=,又E=n,即I∝,所以快速插入时电路中的电流大.
1.感应电动势的相关因素
(1)感应电动势E的大小取决于穿过电路的磁通量变化率和匝数n,而与Φ的大小、ΔΦ的大小没有必然的关系;
(2)感应电动势E的大小与电路的电阻R也无关,但感应电流的大小与E及回路总电阻R都有关.
2.磁通量的变化率在Φ
t图象上是某点切线的斜率.
3.感应电动势E=n的两种基本形式:
(1)当垂直于磁场方向的线圈面积S不变,磁感应强度B发生变化时,ΔΦ=ΔB·S,则E=nS,其中叫磁感应强度B的变化率.
(2)当磁感应强度B不变,垂直于磁场方向的线圈面积S发生变化时,ΔΦ=B·ΔS,则E=nB.
4.E=n求出的是Δt时间内的平均感应电动势.
5.Φ、ΔΦ与三者之间的关系.
物理量
单位
物理意义
计算公式
磁通量Φ
Wb
表示某时刻或某位置时穿过某一面积的磁感线条数的多少
Φ=B·S⊥
磁通量的变化量ΔΦ
Wb
表示在某一过程中穿过某一面积的磁通量变化的多少
ΔΦ=|Φ2-Φ1|
磁通量的变化率
Wb/s
表示穿过某一面积的磁通量变化的快慢
=
1.穿过某闭合回路的磁通量Φ随时间t变化的图象分别如图4 4 2中的①~④所示,下列说法正确的是( )
图4 4 2
A.图①有感应电动势,且大小恒定不变
B.图②产生的感应电动势一直在变大
C.图③在0~t1内的感应电动势大小是在t1~t2内的2倍
D.图④产生的感应电动势先变大再变小
【解析】 感应电动势E=n,而对应Φ t图象中图线切线斜率的绝对值,根据图线切线斜率的变化情况可得①中无感应电动势,②中感应电动势恒定不变,③中感应电动势在0~t1内的大小是在t1~t2内大小的2倍,④中感应电动势先变小再变大,选项C正确.
【答案】 C
2.穿过一个内阻为1
Ω的10匝闭合线圈的磁通量每秒均匀减少2
Wb,则线圈中( )
A.感应电动势每秒增加2
V
B.感应电动势每秒减少2
V
C.磁通量的变化率为2
Wb/s
D.感应电流为2
A
【解析】 磁通量的变化率=2
Wb/s,C正确.由E=n得E=10×2
V=20
V,感应电动势不变,A、B错误.由I=得I=
A=20
A,D错误.
【答案】 C
3.如图4 4 3甲所示,在竖直向上的匀强磁场中,水平放置一个不变形的单匝金属圆线圈,规定线圈中感应电流的正方向如图所示.当磁场的磁感应强度B随时间t做如图乙所示的变化时,图中能正确表示线圈中感应电动势E变化的是( )
甲 乙
图4 4 3
【解析】 由法拉第电磁感应定律,E=n=n,在0~1
s内,B均匀增大,则为一恒量,则E为一恒量,再由楞次定律,可判断感应电动势为顺时针方向,则电动势为正值;在1~3
s内,B不变化,则感应电动势为零;在3~5
s内,B均匀减小,则为一恒量,但B变化得较慢,则E为一恒量,但比前者小,再由楞次定律,可判断感应电动势为逆时针方向,则电动势为负值,所以A选项正确.
【答案】 A
4.一个200匝、面积为20
cm2的线圈,放在磁场中,磁场的方向与线圈平面成30°角,若磁感应强度在0.05
s内由0.1
T
增加到0.5
T,在此过程中磁通量变化了多少?磁通量的平均变化率是多少?线圈中感应电动势的大小是多少?
【解析】 磁通量的变化是由磁场的变化引起的,应该用公式ΔΦ=ΔBSsin
θ来计算,
所以ΔΦ=ΔBSsin
θ=(0.5-0.1)×20×10-4×0.5
Wb=4×10-4
Wb
磁通量的平均变化率
=Wb/s=8×10-3Wb/s
感应电动势的大小可根据法拉第电磁感应定律计算E=n=200×8×10-3V=1.6
V.
【答案】 4×10-4Wb 8×10-3Wb/s 1.6
V
5.如图4 4 4所示,面积为0.2
m2的100匝线圈处在匀强磁场中,磁场方向垂直于线圈平面,已知磁感应强度随时间变化的规律为B=(2+0.2t)T,定值电阻R1=6
Ω,线圈电阻R2=4
Ω,求:
图4 4 4
(1)回路的感应电动势;
(2)流过R1的电流;
(3)a、b两点间电压Uab.
【解析】 (1)=0.2
T/s
E==n·S=100×0.04
V=4
V.
(2)等效电路如图.
根据闭合电路欧姆定律有I==0.4
A.
(3)a、b两点间的电压Uab=IR1=2.4
V.
【答案】 (1)4
V (2)0.4
A (3)2.4
V
计算磁通量ΔΦ的三种方法
1.若磁通量的变化是由回路包围的面积引起的,ΔΦ=B·ΔS.
2.若磁通量的变化是由磁场变化引起的,ΔΦ=ΔB·S.
3.若磁通量的变化是由面积和磁感应强度方向变化引起的,ΔΦ=Φ2-Φ1.
导线切割磁感线产生的感应电动势,反电动势
1.磁场方向、导体棒与导体棒运动方向三者两两垂直时:E=Blv.
2.如图4 4 5所示,导体棒与磁场方向垂直,导体棒的运动方向与导体棒本身垂直,但与磁场方向夹角为θ时,E=Blvsin
θ.
图4 4 5
3.反电动势
(1)定义:电动机转动时,由于切割磁感线,线圈中产生的削弱电源电动势作用的电动势.
(2)作用:阻碍线圈的转动.
1.对于E=Blv中的B、l、v三者必须相互垂直.(√)
2.导体棒在磁场中运动速度越大,产生的感应电动势一定越大.(×)
3.当B、l、v三者大小、方向均不变时,在Δt时间内的平均感应电动势和它在任意时刻产生的瞬时感应电动势相同.(√)
4.电动机通电转动,电动机中出现的感应电动势为反电动势,反电动势会阻碍线圈的运动.(√)
5.电动机正常工作时,反电动势会加快线圈的运动.(×)
6.电动机工作中由于机械阻力过大而停止转动,就没有了反电动势,线圈中的电流会很大,很容易烧毁电动机.(√)
1.如图4 4 6所示,一边长为L的正方形导线框abcd垂直于磁感线,以速度v在匀强磁场中向右运动,甲同学说:由法拉第电磁感应定律可知,这时穿过线框的磁通量的变化率为零,所以线框中感应电动势应该为零.乙同学说线框中ad和bc边均以速度v做切割磁感线运动,由E=BLv可知,这两条边都应该产生电动势且Ead=Ebc=BLv.他们各执一词,到底谁说的对呢?
图4 4 6
【提示】 这两个同学说的并不矛盾,虽然ad边与bc边都产生感应电动势,但由于方向相反,相当于两个电源并联没有对外供电,所以整个回路的电动势为零.可见,用法拉第电磁感应定律求出的是整个回路的感应电动势,而用E=BLv求的是回路中做切割磁感线的那部分导体产生的电动势.
2.电动机工作时,加在电动机上的电压U和流经电动机的电流I及电动机线圈电阻r三者之间是否满足I=?
【提示】 电动机转动时其线圈中要产生一个反电动势U′,加在线圈电阻上的电压Ur远小于U,所以I=不成立.此时线圈中的电流I=.
如图4 4 7所示,一个半径为r的半圆形导体,处在磁感应强度为B的匀强磁场中.
图4 4 7
探讨1:当导体沿OP方向以速度v做匀速运动时,其感应电动势的大小是多少?
【提示】 导线的有效长度l=2r,则感应电动势E=Blv=2Brv.
探讨2:当导体沿MN方向以速度v做匀速运动时,其感应电动势的大小是多少?
【提示】 此时导线的有效长度l=r,则感应电动势E=Blv=Brv.
1.对公式E=Blvsin
θ的理解
(1)若导线垂直切割磁感线时,即B、l、v三者两两垂直,公式中θ=90°,此时E=Blv,感应电动势最大,此式常用来计算瞬时感应电动势.
(2)导线不垂直切割磁感线时,即v与B有一夹角θ时,如图4 4 8所示,此时可将导线的速度v向垂直于磁感线和平行于磁感线两个方向分解,则分速度v2=vcos
θ不使导线切割磁感线,使导线切割磁感线的是分速度v1=vsin
θ,从而使导线产生的感应电动势为E=Blv1=Blvsin
θ.
图4 4 8
(3)若导线是曲折的,则l应是导线的有效切割长度,即导线两端点在v、B所决定平面的垂线上的长度.如图4 4 9甲所示的三种情况下感应电动势相同;如图乙所示的半径为r的圆弧形导体垂直切割磁感线时,感应电动势E=Blv≠2Brv.
甲 乙
图4 4 9
2.公式E=n与E=Blvsin
θ的区别与联系
E=n
E=Blvsin
θ
区别
研究对象
某个回路
回路中做切割磁感线运动的那部分导体
研究内容
(1)求的是Δt时间内的平均感应电动势,E与某段时间或某个过程对应(2)当Δt→0时,E为瞬时感应电动势
(1)若v为瞬时速度,公式求的是瞬时感应电动势(2)若v为平均速度,公式求的是平均感应电动势(3)当B、l、v三者均不变时,平均感应电动势与瞬时感应电动势相等
适用范围
对任何电路普遍适用
只适用于导体切割磁感线运动的情况
联系
(1)E=Blvsin
θ可由E=n在一定条件下推导出来(2)整个回路的感应电动势为零时,回路中某段导体的感应电动势不一定为零
3.导体棒转动切割磁感线时的感应电动势
如图4 4 10所示,长为l的导体棒ab以a为圆心,以角速度ω在磁感应强度为B的匀强磁场中匀速转动,其感应电动势可从两个角度推导.
图4 4 10
(1)棒上各点速度不同,其平均速度=ωl,由E=Blv得棒上感应电动势大小为E=Bl·ωl=Bl2ω.
(2)若经时间Δt,棒扫过的面积为ΔS=πl2=l2ωΔt,磁通量的变化量ΔΦ=B·ΔS=Bl2ωΔt,由E=得棒上感应电动势大小为E=Bl2ω.
6.如图4 4 11所示,MN、PQ为两条平行的水平放置的金属导轨,左端接有定值电阻R,金属棒ab斜放在两导轨之间,与导轨接触良好,ab=L.磁感应强度为B的匀强磁场垂直于导轨平面,设金属棒与两导轨间夹角为60°,以速度v水平向右匀速运动,不计导轨和棒的电阻,则流过金属棒中的电流为( )
图4 4 11
A.I=
B.I=
C.I=
D.I=
【解析】 导体棒切割磁感线的有效长度为:L·sin
60°=L,故感应电动势E=Bv,由闭合电路欧姆定律得I=,故选项B正确.
【答案】 B
7.如图4 4 12是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为r,匀强磁场的磁感应强度为B,回路总电阻为R,匀速转动铜盘的角速度为ω.则电路的功率是( )
图4 4 12
A.
B.
C.
D.
【解析】 根据导体棒旋转切割产生电动势E=Bωr2,由P=,得电路的功率是,故选项C正确.
【答案】 C
8.在范围足够大,磁感应强度B=0.2
T,方向竖直向下的匀强磁场中,有一水平放置的光滑框架,宽度l=0.4
m,如图4 4 13所示,框架上放置一质量为0.05
kg、电阻为1
Ω的金属杆cd,框架电阻不计.若金属杆cd以恒定的加速度a=2
m/s2由静止开始水平向右做匀变速运动,求:
图4 4 13
(1)前5
s内平均感应电动势的大小;
(2)第5
s末,回路中电流的大小.
【解析】 (1)前5
s内的位移x=at2=25
m
前5
s内的平均速度==5
m/s
故平均感应电动势的大小E=Bl=0.4
V.
(2)第5
s末速度v′=at=10
m/s
此时感应电动势E′=Blv′
则回路中电流的大小I===0.8
A.
【答案】 (1)0.4
V (2)0.8
A
9.如图4 4 14所示,在磁感应强度为0.2
T的匀强磁场中,有一长为0.5
m、电阻为1.0
Ω的导体AB在金属框架上以10
m/s的速度向右滑动,R1=R2=2.0
Ω,其他电阻不计,求流过R1的电流I1.
图4 4 14
【解析】 AB切割磁感线相当于电源,其等效电路如图所示,
E=Blv=0.2×0.5×10
V=1
V
由闭合电路欧姆定律得I=,R1、R2并联,由并联电路电阻关系得=+
解得:R==1.0
Ω
所以IAB=I=0.5
A
因为R1=R2,所以流过R1的电流为I1==0.25
A.
【答案】 0.25
A
电磁感应中电路问题的分析方法
1.明确哪部分导体或电路产生感应电动势,该导体或电路就是电源,其他部分是外电路.
2.用法拉第电磁感应定律或切割公式确定感应电动势的大小,用楞次定律或右手定则确定感应电动势的方向.
3.分清内外电路,画出等效电路图.
4.运用闭合电路欧姆定律、串并联电路特点、电功率、电热等公式联立求解.
