湖南省浏阳二中2016-2017学年高二下学期升高三摸底考试数学理试卷
文档属性
| 名称 | 湖南省浏阳二中2016-2017学年高二下学期升高三摸底考试数学理试卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 362.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-13 23:12:06 | ||
图片预览



文档简介
2017年上学期高二升高三摸底考试数学(理)试卷
时量:120分钟
总分:150分
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的
1.已知集合A={x|y=},B={x|﹣1≤2x﹣1≤3},则A∩B=( )
A.[0,1]
B.[1,2]
C.[1,]
D.[0,2]
2.设i是虚数单位,若复数的共轭复数为z,则|z|=( )
A.i+2
B.i﹣2
C.
D.5
3.命题“ x0≤0,使得x02≥0”的否定是( )
A. x≤0,x2<0
B. x≤0,x2≥0
C. x0>0,x02>0
D. x0<0,x02≤0
4.已知双曲线的离心率为,则双曲线的渐近线方程为( )
A.
B.
C.y=±2x
D.
5.在△ABC中,
=,
=,若点D满足=,则=( )
A.
+
B.
+
C.
+
D.
+
6.将函数y=3sinx的图象向右平移个单位长度,所得图象对应的函数( )
A.在区间[,]上单调递减
B.在区间[0,]上单调增
C.在区间[0,π]上单调递减
D.在区间[0,π]上单调增
7.等差数列{an}的前n项和为Sn,若a1=2,S3=12,则S6等于( )
A.84
B.57
C.45
D.42
8.
函数,则函数的导数的图象是(
)
A
B
C
D
9.利用计算机在区间(0,1)上产生随机数a,则使不等式9a2﹣9a+2<0成立的概率是( )
A.
B.
C.
D.
10..某几何体的三视图如图所示,则它的体积是
(
)
11.在二项式(x2﹣)5的展开式中,记x4的系数为a,
则dx=( )
A.
B.
C.
D.π
12.若函数f(x)=4x2+2x﹣2+mex有两个不同的零点,则实数m取值范围为( )
A.[0,1)
B.[0,2)∪{﹣}
C.(0,2)∪{﹣}
D.[0,2)∪{﹣}
二、填空题:本大题共4小题,每小题5分,共20分。请把正确的答案填在答题卡相应的横线上
13.某程序框图如图所示,当输出y的值为时,则输出x的值为______
14.已知都是实数,命题;命题,
则是的______条件.
15.过抛物线y2=4x的焦点作直线l,交抛物线于A,B两点,
若线段AB中点的横坐标为3,则|AB|等于 .
16.已知数列{an}满足:2an=an+1+an﹣1(n≥2,n∈N
),且a1>0,
a1、3、a3依次成等比数列,则数列{an}前四项和的最小值为 .
三、解答题:本大题必做题5小题,选做题3小题,共70分。解答应写出文字说明,证明过程或演算步骤.
17.在△ABC中,内角A,B,C的对边分别为a,b,c,
已知2a2=2b2+2c2﹣bc,且a=2b,
(1)
求cosA;
(2)求cos(A﹣B)..(
12分)
18.某大学自主招生分笔试和面试两部分,老师把参加笔试的
40
名学生的成绩分组:
第1组[75,80),第2组
[80,85),第3组[85,
90),第4组
[90,
95),第5组[95,100),得到频率分布直方图如图所示:
分别求成绩在第4,5组的人数;
若该教师决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名进入面试,
①已知甲和乙的成绩均在第3组,求甲和乙同时进入面试的概率;
②若决定在这6名学生中随机抽取2名学生接受考官
D
的面试,设第4组中有X名学生被考官D面试,求X的分布列和数学期望.(
12分)
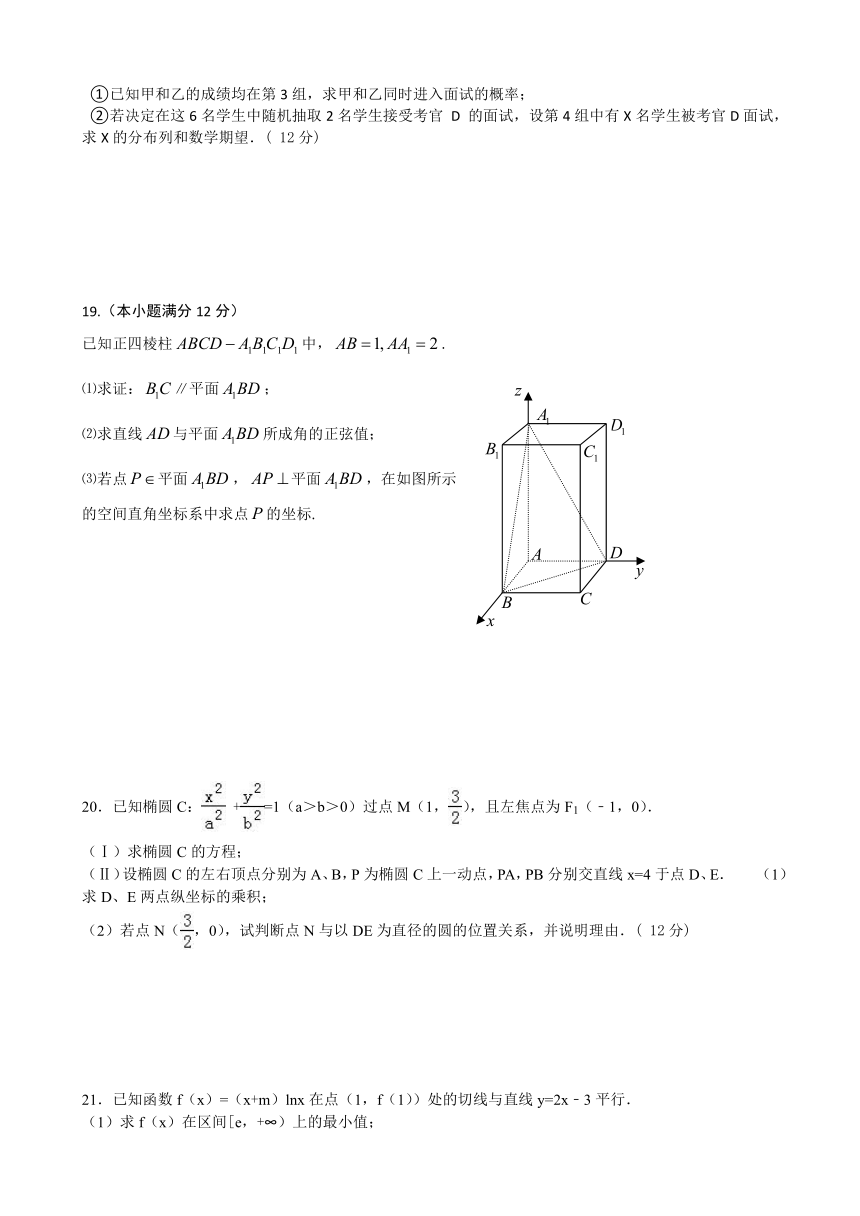
19.(本小题满分12分)
已知正四棱柱中,.
⑴求证:∥平面;
⑵求直线与平面所成角的正弦值;
⑶若点平面,平面,在如图所示
的空间直角坐标系中求点的坐标.
20.已知椭圆C:
+=1(a>b>0)过点M(1,),且左焦点为F1(﹣1,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)设椭圆C的左右顶点分别为A、B,P为椭圆C上一动点,PA,PB分别交直线x=4于点D、E.
(1)求D、E两点纵坐标的乘积;
(2)若点N(,0),试判断点N与以DE为直径的圆的位置关系,并说明理由.(
12分)
21.已知函数f(x)=(x+m)lnx在点(1,f(1))处的切线与直线y=2x﹣3平行.
(1)求f(x)在区间[e,+∞)上的最小值;
(2)若对任意x∈(0,1),都有f(x)+2﹣2x<0成立,求实数a的取值范围.(
12分)
请考生在(22),(23)两题中任选一题作答,如果多做,则按所做的第一个题计分
[选修4-4:坐标系与参数方程]
22.已知极坐标系的极点与直角坐标系的原点O重合,极轴与x轴的正半轴重合.曲线C1:ρcos(θ﹣)=,曲线C2:(t为参数).
(1)写出曲线C1的直角坐标方程和C2的普通方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)(
10分)
[选修4-5:不等式选讲]
23.已知函数f(x)=|2x+1|﹣|x|﹣2.
(1)解不等式f(x)≥0;
(2)若对任意的实数x,都有f(x)﹣2a2≥|x|﹣3a﹣2,求实数a的取值范围.(
10分)
2017年上学期高二升高三摸底考试数学(理)参考答案与试题解析
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的
1.
B.
2.
C.
3.
A.
4.B
5.C.
6.D.
7.
D.
8.
C.
9.
A.
10.D
11.
A.
12.D.
12【解答】解:由f(x)=4x2+2x﹣2+mex=0得﹣mex=4x2+2x﹣2,得m=﹣,
设h(x)=﹣,则h′(x)=﹣==由h′(x)>0得x>2或x<,此时函数递增,由h′(x)<0得<x<2,此时函数递减,即当x=2时,函数取得极小值h(2)=﹣=﹣,
当x=﹣时,函数取得极大值h(﹣)=﹣=2,
当x→+∞时,h(x)<0,当x→﹣∞时,h(x)→﹣∞,则函数h(x)对应的图象如图:
若函数f(x)=4x2+2x﹣2+mex有两个不同的零点,等价为m=﹣有两个不同的根,
则0≤m<2或m=﹣,即实数m的取值范围是[0,2)∪{﹣},故选:D
二、填空题:本大题共4小题,每小题5分,共20分。
13.16
14.充分不必要
15.8
16. 6 .
16.【解答】解:∵2an=an+1+an﹣1(n≥2,n∈N ),
∴{an}是等差数列.∵a1、3、a3依次成等比数列,
∴9=a1(a1+2d),∴d=﹣a1,数列{an}前四项和S=4a1+6d=a1+,
∵a1>0,∴S≥=6,∴数列{an}前四项和的最小值为6.故答案为:6.
三、解答题:本大题必做题5小题,选做题3小题,共70分。解答应写出文字说明,证明过程或演算步骤.
17.【解答】(本题满分为12分)
解:(1)∵2a2=2b2+2c2﹣bc,可得:a2=b2+c2﹣bc,
∴由余弦定理可得:cosA===,…3分
(2)∵cosA>0,0<A<,
∴sinA===…5分
由a=2b,根据正弦定理可得:sinA=2sinB,可得sinB=sinA=,…7分
∵A>B,∴0<B<,∴cosB===,…9分
∴cos(A﹣B)=cosAcosB+sinAsinB=+=…12分
18.(本小题满分12分)
解(Ⅰ)第4组学生人数为
,第5组人数为
所以第4,5组的学生人数分别为8人,4人
-----------------------------------------4分
(Ⅱ)①因为第3组学生人数为,所以第3,4,5中抽取的人数分别是
3人,2人,1人,则甲,乙同时进入面试的概率为
---------------------8分
②由①知,X的可能取值为0,1,2所以
X分布列为
X
0
1
2
P
---------------------------------------------
12分
19.
(本小题满分12分)
解:⑴证明:∵
,
∴四边形为平行四边形,∥,
又平面,平面,
所以∥平面
4分
⑵在如图所示的空间直角坐标系中,
,
设平面的一个法向量为,则
,取得,
,
所以直线与平面所成角的正弦值为
8分
⑶因为点到平面的距离为,
所以,即点的坐标为。
12分
20.【解答】解:(Ⅰ)由题意可得c=1,将点M(1,)代入椭圆方程,
可得+=1,又a2﹣b2=1,解得a=2,b=,
则椭圆的方程为+=1;
(Ⅱ)(1)设P(m,n),则+=1,
即有n2=3(1﹣)=﹣,A(﹣2,0),B(2,0),设D(4,yD),E(4,yE),
由A,P,D共线,可得则kPA=kAD,即为=,
同理可得=,两式相乘,可得=,
则yDyE=12 (﹣) =﹣9;
即有D、E两点纵坐标的乘积为﹣9;
(2)点N在以DE为直径的圆内.
理由:椭圆的右准线为x=4,
设点Q(x,y)是以DE为直径圆上的任意一点,则 =0,
设D(4,y1),E(4,y2),
可得以DE为直径圆的方程为(x﹣4)(x﹣4)+(y﹣y1)(y﹣y2)=0,
由A,P,D共线可得=,可设y1=6k1,
同理可得y2=2k2,
又k1 k2=﹣,
即有x2+y2﹣8x﹣(6k1+2k2)y+7=0.
将N(,0)代入上式的左边,可得
+0﹣8×﹣0+7=﹣<0,
即有点N在以DE为直径的圆内.
21.【解答】解:(1)由f′(x)=lnx+结合题意得:
函数f(x)在点(1,f(1))处的切线的斜率k=f′(1)=1+m=2,
∴m=1,
∵x∈[e,+∞)时,f′(x)=lnx+>0,
∴函数f(x)在[e,+∞)递增,
∴f(x)min=f(e)=e+1;
(2)对任意x∈(0,1),都有f(x)+2﹣2x<0成立,
即lnx+2(1﹣x)<0对任意x∈(0,1)恒成立①,
当x∈(0,1)知lnx<0,
a<0时,
lnx+2(1﹣x)>0,不合题意,
a>0时,① lnx+<0对任意x∈(0,1)恒成立,
记h(x)=lnx+,则h′(x)=,
记g(x)=x2+2(1﹣2a)x+1,则方程g(x)=0的根的判别式△=4(1﹣2a)2﹣4=16a(a﹣1),
若a≤1,则△≤0,g(x)≥0,在(0,1]上h′(x)≥0,
∴h(x)在(0,1]上递增,又h(1)=0,
∴对任意x∈(0,1),h(x)<0恒成立,
若a>1,△>0,由g(0)=1>0,g(1)=4(1﹣a)<0知存在x0∈(0,1)使得g(x0)=0,
对任意x∈(x0,1),g(x)<0,h′(x)<0,
∴h(x)在(x0,1)递减,又h(1)=0,
∴x∈(x0,1)时,h(x)>0不合题意,
综上,a∈(0,1].
请考生在(22),(23)两题中任选一题作答,如果多做,则按所做的第一个题计分.
[选修4-4:坐标系与参数方程]
22.【解答】解:(1)∵ρcos(θ﹣)= ρcosθ+ρsinθ=2,①
将代入①即可得到曲线C1的直角坐标方程:x+y﹣2=0,
将消去参数t,得到曲线C2的普通方程为(x﹣4)2+(y﹣5)2=25;
(2)由,联立解得:或,
将转化成极坐标(,),
将转化成极坐标(2,),
∴C1与C2交点的极坐标(,),(2,).
[选修4-5:不等式选讲]
23.【解答】解:(1)由不等式f(x)=|2x+1|﹣|x|﹣2≥0,可得①,或②,或③.
解①求得x≤﹣3;解②求得x∈ ,解③求得
x≥1.
综上可得,原不等式的解集为{x|x≤﹣3,或
x≥1}.
(2)若对任意的实数x,都有f(x)﹣2a2≥|x|﹣3a﹣2,则|2x+1|﹣2|x|≥2a2﹣3a
恒成立.
又∵|2x+1|﹣2|x|≤|2x+1﹣2x|=1,∴2a2﹣3a≤1,解得≤a≤1,
即实数a的取值范围为[,1].
侧视图
正视图
俯视图
时量:120分钟
总分:150分
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的
1.已知集合A={x|y=},B={x|﹣1≤2x﹣1≤3},则A∩B=( )
A.[0,1]
B.[1,2]
C.[1,]
D.[0,2]
2.设i是虚数单位,若复数的共轭复数为z,则|z|=( )
A.i+2
B.i﹣2
C.
D.5
3.命题“ x0≤0,使得x02≥0”的否定是( )
A. x≤0,x2<0
B. x≤0,x2≥0
C. x0>0,x02>0
D. x0<0,x02≤0
4.已知双曲线的离心率为,则双曲线的渐近线方程为( )
A.
B.
C.y=±2x
D.
5.在△ABC中,
=,
=,若点D满足=,则=( )
A.
+
B.
+
C.
+
D.
+
6.将函数y=3sinx的图象向右平移个单位长度,所得图象对应的函数( )
A.在区间[,]上单调递减
B.在区间[0,]上单调增
C.在区间[0,π]上单调递减
D.在区间[0,π]上单调增
7.等差数列{an}的前n项和为Sn,若a1=2,S3=12,则S6等于( )
A.84
B.57
C.45
D.42
8.
函数,则函数的导数的图象是(
)
A
B
C
D
9.利用计算机在区间(0,1)上产生随机数a,则使不等式9a2﹣9a+2<0成立的概率是( )
A.
B.
C.
D.
10..某几何体的三视图如图所示,则它的体积是
(
)
11.在二项式(x2﹣)5的展开式中,记x4的系数为a,
则dx=( )
A.
B.
C.
D.π
12.若函数f(x)=4x2+2x﹣2+mex有两个不同的零点,则实数m取值范围为( )
A.[0,1)
B.[0,2)∪{﹣}
C.(0,2)∪{﹣}
D.[0,2)∪{﹣}
二、填空题:本大题共4小题,每小题5分,共20分。请把正确的答案填在答题卡相应的横线上
13.某程序框图如图所示,当输出y的值为时,则输出x的值为______
14.已知都是实数,命题;命题,
则是的______条件.
15.过抛物线y2=4x的焦点作直线l,交抛物线于A,B两点,
若线段AB中点的横坐标为3,则|AB|等于 .
16.已知数列{an}满足:2an=an+1+an﹣1(n≥2,n∈N
),且a1>0,
a1、3、a3依次成等比数列,则数列{an}前四项和的最小值为 .
三、解答题:本大题必做题5小题,选做题3小题,共70分。解答应写出文字说明,证明过程或演算步骤.
17.在△ABC中,内角A,B,C的对边分别为a,b,c,
已知2a2=2b2+2c2﹣bc,且a=2b,
(1)
求cosA;
(2)求cos(A﹣B)..(
12分)
18.某大学自主招生分笔试和面试两部分,老师把参加笔试的
40
名学生的成绩分组:
第1组[75,80),第2组
[80,85),第3组[85,
90),第4组
[90,
95),第5组[95,100),得到频率分布直方图如图所示:
分别求成绩在第4,5组的人数;
若该教师决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名进入面试,
①已知甲和乙的成绩均在第3组,求甲和乙同时进入面试的概率;
②若决定在这6名学生中随机抽取2名学生接受考官
D
的面试,设第4组中有X名学生被考官D面试,求X的分布列和数学期望.(
12分)
19.(本小题满分12分)
已知正四棱柱中,.
⑴求证:∥平面;
⑵求直线与平面所成角的正弦值;
⑶若点平面,平面,在如图所示
的空间直角坐标系中求点的坐标.
20.已知椭圆C:
+=1(a>b>0)过点M(1,),且左焦点为F1(﹣1,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)设椭圆C的左右顶点分别为A、B,P为椭圆C上一动点,PA,PB分别交直线x=4于点D、E.
(1)求D、E两点纵坐标的乘积;
(2)若点N(,0),试判断点N与以DE为直径的圆的位置关系,并说明理由.(
12分)
21.已知函数f(x)=(x+m)lnx在点(1,f(1))处的切线与直线y=2x﹣3平行.
(1)求f(x)在区间[e,+∞)上的最小值;
(2)若对任意x∈(0,1),都有f(x)+2﹣2x<0成立,求实数a的取值范围.(
12分)
请考生在(22),(23)两题中任选一题作答,如果多做,则按所做的第一个题计分
[选修4-4:坐标系与参数方程]
22.已知极坐标系的极点与直角坐标系的原点O重合,极轴与x轴的正半轴重合.曲线C1:ρcos(θ﹣)=,曲线C2:(t为参数).
(1)写出曲线C1的直角坐标方程和C2的普通方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)(
10分)
[选修4-5:不等式选讲]
23.已知函数f(x)=|2x+1|﹣|x|﹣2.
(1)解不等式f(x)≥0;
(2)若对任意的实数x,都有f(x)﹣2a2≥|x|﹣3a﹣2,求实数a的取值范围.(
10分)
2017年上学期高二升高三摸底考试数学(理)参考答案与试题解析
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的
1.
B.
2.
C.
3.
A.
4.B
5.C.
6.D.
7.
D.
8.
C.
9.
A.
10.D
11.
A.
12.D.
12【解答】解:由f(x)=4x2+2x﹣2+mex=0得﹣mex=4x2+2x﹣2,得m=﹣,
设h(x)=﹣,则h′(x)=﹣==由h′(x)>0得x>2或x<,此时函数递增,由h′(x)<0得<x<2,此时函数递减,即当x=2时,函数取得极小值h(2)=﹣=﹣,
当x=﹣时,函数取得极大值h(﹣)=﹣=2,
当x→+∞时,h(x)<0,当x→﹣∞时,h(x)→﹣∞,则函数h(x)对应的图象如图:
若函数f(x)=4x2+2x﹣2+mex有两个不同的零点,等价为m=﹣有两个不同的根,
则0≤m<2或m=﹣,即实数m的取值范围是[0,2)∪{﹣},故选:D
二、填空题:本大题共4小题,每小题5分,共20分。
13.16
14.充分不必要
15.8
16. 6 .
16.【解答】解:∵2an=an+1+an﹣1(n≥2,n∈N ),
∴{an}是等差数列.∵a1、3、a3依次成等比数列,
∴9=a1(a1+2d),∴d=﹣a1,数列{an}前四项和S=4a1+6d=a1+,
∵a1>0,∴S≥=6,∴数列{an}前四项和的最小值为6.故答案为:6.
三、解答题:本大题必做题5小题,选做题3小题,共70分。解答应写出文字说明,证明过程或演算步骤.
17.【解答】(本题满分为12分)
解:(1)∵2a2=2b2+2c2﹣bc,可得:a2=b2+c2﹣bc,
∴由余弦定理可得:cosA===,…3分
(2)∵cosA>0,0<A<,
∴sinA===…5分
由a=2b,根据正弦定理可得:sinA=2sinB,可得sinB=sinA=,…7分
∵A>B,∴0<B<,∴cosB===,…9分
∴cos(A﹣B)=cosAcosB+sinAsinB=+=…12分
18.(本小题满分12分)
解(Ⅰ)第4组学生人数为
,第5组人数为
所以第4,5组的学生人数分别为8人,4人
-----------------------------------------4分
(Ⅱ)①因为第3组学生人数为,所以第3,4,5中抽取的人数分别是
3人,2人,1人,则甲,乙同时进入面试的概率为
---------------------8分
②由①知,X的可能取值为0,1,2所以
X分布列为
X
0
1
2
P
---------------------------------------------
12分
19.
(本小题满分12分)
解:⑴证明:∵
,
∴四边形为平行四边形,∥,
又平面,平面,
所以∥平面
4分
⑵在如图所示的空间直角坐标系中,
,
设平面的一个法向量为,则
,取得,
,
所以直线与平面所成角的正弦值为
8分
⑶因为点到平面的距离为,
所以,即点的坐标为。
12分
20.【解答】解:(Ⅰ)由题意可得c=1,将点M(1,)代入椭圆方程,
可得+=1,又a2﹣b2=1,解得a=2,b=,
则椭圆的方程为+=1;
(Ⅱ)(1)设P(m,n),则+=1,
即有n2=3(1﹣)=﹣,A(﹣2,0),B(2,0),设D(4,yD),E(4,yE),
由A,P,D共线,可得则kPA=kAD,即为=,
同理可得=,两式相乘,可得=,
则yDyE=12 (﹣) =﹣9;
即有D、E两点纵坐标的乘积为﹣9;
(2)点N在以DE为直径的圆内.
理由:椭圆的右准线为x=4,
设点Q(x,y)是以DE为直径圆上的任意一点,则 =0,
设D(4,y1),E(4,y2),
可得以DE为直径圆的方程为(x﹣4)(x﹣4)+(y﹣y1)(y﹣y2)=0,
由A,P,D共线可得=,可设y1=6k1,
同理可得y2=2k2,
又k1 k2=﹣,
即有x2+y2﹣8x﹣(6k1+2k2)y+7=0.
将N(,0)代入上式的左边,可得
+0﹣8×﹣0+7=﹣<0,
即有点N在以DE为直径的圆内.
21.【解答】解:(1)由f′(x)=lnx+结合题意得:
函数f(x)在点(1,f(1))处的切线的斜率k=f′(1)=1+m=2,
∴m=1,
∵x∈[e,+∞)时,f′(x)=lnx+>0,
∴函数f(x)在[e,+∞)递增,
∴f(x)min=f(e)=e+1;
(2)对任意x∈(0,1),都有f(x)+2﹣2x<0成立,
即lnx+2(1﹣x)<0对任意x∈(0,1)恒成立①,
当x∈(0,1)知lnx<0,
a<0时,
lnx+2(1﹣x)>0,不合题意,
a>0时,① lnx+<0对任意x∈(0,1)恒成立,
记h(x)=lnx+,则h′(x)=,
记g(x)=x2+2(1﹣2a)x+1,则方程g(x)=0的根的判别式△=4(1﹣2a)2﹣4=16a(a﹣1),
若a≤1,则△≤0,g(x)≥0,在(0,1]上h′(x)≥0,
∴h(x)在(0,1]上递增,又h(1)=0,
∴对任意x∈(0,1),h(x)<0恒成立,
若a>1,△>0,由g(0)=1>0,g(1)=4(1﹣a)<0知存在x0∈(0,1)使得g(x0)=0,
对任意x∈(x0,1),g(x)<0,h′(x)<0,
∴h(x)在(x0,1)递减,又h(1)=0,
∴x∈(x0,1)时,h(x)>0不合题意,
综上,a∈(0,1].
请考生在(22),(23)两题中任选一题作答,如果多做,则按所做的第一个题计分.
[选修4-4:坐标系与参数方程]
22.【解答】解:(1)∵ρcos(θ﹣)= ρcosθ+ρsinθ=2,①
将代入①即可得到曲线C1的直角坐标方程:x+y﹣2=0,
将消去参数t,得到曲线C2的普通方程为(x﹣4)2+(y﹣5)2=25;
(2)由,联立解得:或,
将转化成极坐标(,),
将转化成极坐标(2,),
∴C1与C2交点的极坐标(,),(2,).
[选修4-5:不等式选讲]
23.【解答】解:(1)由不等式f(x)=|2x+1|﹣|x|﹣2≥0,可得①,或②,或③.
解①求得x≤﹣3;解②求得x∈ ,解③求得
x≥1.
综上可得,原不等式的解集为{x|x≤﹣3,或
x≥1}.
(2)若对任意的实数x,都有f(x)﹣2a2≥|x|﹣3a﹣2,则|2x+1|﹣2|x|≥2a2﹣3a
恒成立.
又∵|2x+1|﹣2|x|≤|2x+1﹣2x|=1,∴2a2﹣3a≤1,解得≤a≤1,
即实数a的取值范围为[,1].
侧视图
正视图
俯视图
同课章节目录
