陕西省黄陵中学2016-2017学年高二(普通班)下学期期末考试数学(文)试题 Word版含答案
文档属性
| 名称 | 陕西省黄陵中学2016-2017学年高二(普通班)下学期期末考试数学(文)试题 Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 206.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-15 00:00:00 | ||
图片预览


文档简介
黄陵中学2016~2017学年第二学期
高二普通班文科期末数学试题
一、选择题:本大题共12小题,每小题5分,共60分
1.
已知集合M={1,2,zi},i为虚数单位,N=
{3,4},M∩N={4},则复数z=(
)
A.-2i B.2i
C.-4i
D.4i
2.
执行下面的程序框图,如果输入的
t∈,则输出的s属于(
)
A. B.
C.
D.
3.
设a,b是正实数,以下不等式:
(1)a+≥2;(2)≥a+b;(3)≥;(4)a<|a-b|+b,其中恒成立的有(
)
A.(1)(2)
B.(2)(3)
C.(3)(4)
D.(2)(4)
4.
下列各式中,最小值等于的是(
)
A.
B.
C.
D.
5.下面使用类比推理恰当的是( )
A.“若a 3=b 3,则a=b”类推出“若a 0=b 0,则a=b”
B.“若(a+b)c=ac+bc”类推出“(a b)c=ac bc”
C.“(a+b)c=ac+bc”类推出“=+(c≠0)”
D.“(ab)n=anbn”类推出“(a+b)n=an+bn”
6.若直线的参数方程为,则直线的斜率为(
)
A.
B.
C.
D.
7.
下列在曲线上的点是(
)
A.
B.
C.
D.
8.点的直角坐标是,则点的极坐标为(
)
A.
B.
C.
D.
9.分析法是从要证明的结论出发,逐步寻求使结论成立的( )
A.充分条件
B.必要条件
C.充要条件
D.等价条件
10.
极坐标方程表示的曲线为(
)
A.一条射线和一个圆
B.两条直线
C.一条直线和一个圆
D.一个圆
11.
将参数方程化为普通方程为(
)
A.
B.
C.
D.
12.
在下列命题中,正确命题的个数是( )
①两个复数不能比较大小;
②复数z=i﹣1对应的点在第四象限;
③若(x2﹣1)+(x2+3x+2)i是纯虚数,则实数x=±1;
④若(z1﹣z2)2+(z2﹣z3)2=0,则z1=z2=z3.
A.0
B.1
C.2
D.3
二.填空题:本大题共4小题,每小题5分,共20分。把答案填在答题卡的相应位置。
13.
若(1+i)(2+i)=a+bi,其中a,b∈R,i为虚数单位,则a+b=_______.
14.
极坐标方程分别为与的两个圆的圆心距为__________。15.若,则,
,
,
按由小到大的顺序排列为_______.
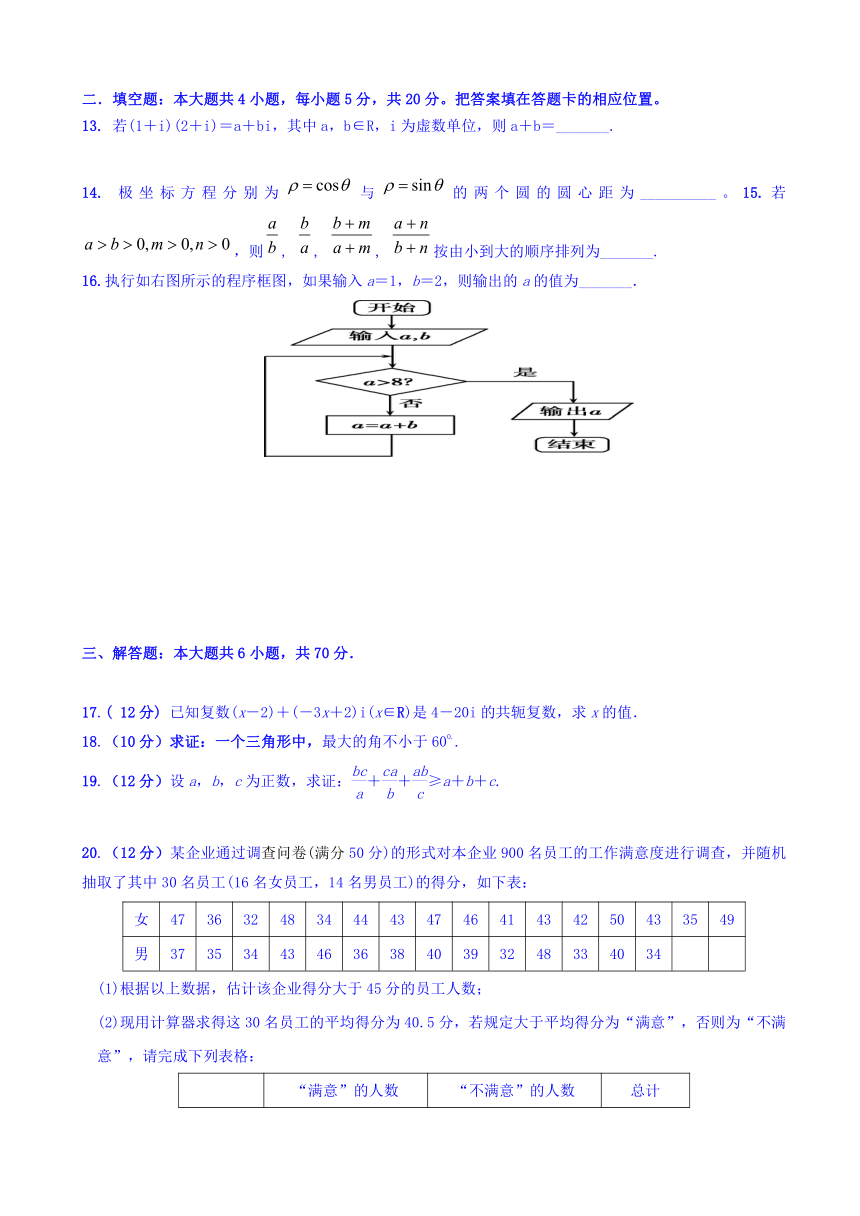
16.执行如右图所示的程序框图,如果输入a=1,b=2,则输出的a的值为_______.
三、解答题:本大题共6小题,共70分.
17.(
12分)
已知复数(x-2)+(-3x+2)i(x∈R)是4-20i的共轭复数,求x的值.
18.(10分)求证:一个三角形中,最大的角不小于600..
19.(12分)设a,b,c为正数,求证:++≥a+b+c.
20.(12分)某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意度进行调查,并随机抽取了其中30名员工(16名女员工,14名男员工)的得分,如下表:
女
47
36
32
48
34
44
43
47
46
41
43
42
50
43
35
49
男
37
35
34
43
46
36
38
40
39
32
48
33
40
34
(1)根据以上数据,估计该企业得分大于45分的员工人数;
(2)现用计算器求得这30名员工的平均得分为40.5分,若规定大于平均得分为“满意”,否则为“不满意”,请完成下列表格:
“满意”的人数
“不满意”的人数
总计
女
16
男
14
总计
30
(3)根据上述表中数据,利用独立性检验的方法判断,能否有99%的把握认为该企业员工“性别”与“工作是否满意”有关?
21.
(12分)求直线和直线的交点的坐标,及点与的距离。
(12分)在椭圆上找一点,使这一点到直线的距离的最小值。
答案
一.选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
B
D
B
D
B
C
A
C
C
A
.二.填空题(共4小题)
13.9
14. 4
15.
16.
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题12分)
已知复数+x-2+(-3x+2)i(x∈R)是4-20i的共轭复数,求x的值.
解:因为复数4-20i的共轭复数为4+20i,由题意得x2+x-2+(x2-3x+2)i=4+20i,根据复数相等的定义,得方程①的解为x=-3或x=2,方程②的解为x=-3或x=6,所以x=-3.
18.(本小题10分)求证:一个三角形中,最大的角不小于600..
答案在选修1-2
的58页
19.(本小题12分)设a,b,c为正数,
求证:++≥a+b+c.
证明:∵a,b,c均是正数,
∴,,均是正数,
∴+≥2c,+≥2a,+≥2b.
三式相加,得2(++)≥2(a+b+c),∴++≥a+b+c.
20.(本小题12分)某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意度进行调查,并随机抽取了其中30名员工(16名女员工,14名男员工)的得分,如下表:
女
47
36
32
48
34
44
43
47
46
41
43
42
50
43
35
49
男
37
35
34
43
46
36
38
40
39
32
48
33
40
34
(1)根据以上数据,估计该企业得分大于45分的员工人数;
(2)现用计算器求得这30名员工的平均得分为40.5分,若规定大于平均得分为“满意”,否则为“不满意”,请完成下列表格:
“满意”的人数
“不满意”的人数
总计
女
16
男
14
总计
30
(3)根据上述表中数据,利用独立性检验的方法判断,能否有99%的把握认为该企业员工“性别”与“工作是否满意”有关?
解 (1)从表中可知,30名员工中有8名得分大于45分,
所以任选一名员工,他(她)的得分大于45分的概率是=,所以估计此次调查中,该单位约有900×=240名员工的得分大于45分.
(2)由题意可得下列表格:
“满意”的人数
“不满意”的人数
总计
女
12
4
16
男
3
11
14
总计
15
15
30
(3)假设H0:“性别”与“工作是否满意”无关,
根据表中数据,求得χ2=≈8.571>6.635,
所以有99%的把握认为“性别”与“工作是否满意”有关.
21.
(本小题12分)求直线和直线的交点的坐标,及点与的距离。
将代入得,
得,而,得
22.
(本小题12分)在椭圆上找一点,使这一点到直线的距离的最小值。
解:设椭圆的参数方程为,
当时,,此时所求点为。
高二普通班文科期末数学试题
一、选择题:本大题共12小题,每小题5分,共60分
1.
已知集合M={1,2,zi},i为虚数单位,N=
{3,4},M∩N={4},则复数z=(
)
A.-2i B.2i
C.-4i
D.4i
2.
执行下面的程序框图,如果输入的
t∈,则输出的s属于(
)
A. B.
C.
D.
3.
设a,b是正实数,以下不等式:
(1)a+≥2;(2)≥a+b;(3)≥;(4)a<|a-b|+b,其中恒成立的有(
)
A.(1)(2)
B.(2)(3)
C.(3)(4)
D.(2)(4)
4.
下列各式中,最小值等于的是(
)
A.
B.
C.
D.
5.下面使用类比推理恰当的是( )
A.“若a 3=b 3,则a=b”类推出“若a 0=b 0,则a=b”
B.“若(a+b)c=ac+bc”类推出“(a b)c=ac bc”
C.“(a+b)c=ac+bc”类推出“=+(c≠0)”
D.“(ab)n=anbn”类推出“(a+b)n=an+bn”
6.若直线的参数方程为,则直线的斜率为(
)
A.
B.
C.
D.
7.
下列在曲线上的点是(
)
A.
B.
C.
D.
8.点的直角坐标是,则点的极坐标为(
)
A.
B.
C.
D.
9.分析法是从要证明的结论出发,逐步寻求使结论成立的( )
A.充分条件
B.必要条件
C.充要条件
D.等价条件
10.
极坐标方程表示的曲线为(
)
A.一条射线和一个圆
B.两条直线
C.一条直线和一个圆
D.一个圆
11.
将参数方程化为普通方程为(
)
A.
B.
C.
D.
12.
在下列命题中,正确命题的个数是( )
①两个复数不能比较大小;
②复数z=i﹣1对应的点在第四象限;
③若(x2﹣1)+(x2+3x+2)i是纯虚数,则实数x=±1;
④若(z1﹣z2)2+(z2﹣z3)2=0,则z1=z2=z3.
A.0
B.1
C.2
D.3
二.填空题:本大题共4小题,每小题5分,共20分。把答案填在答题卡的相应位置。
13.
若(1+i)(2+i)=a+bi,其中a,b∈R,i为虚数单位,则a+b=_______.
14.
极坐标方程分别为与的两个圆的圆心距为__________。15.若,则,
,
,
按由小到大的顺序排列为_______.
16.执行如右图所示的程序框图,如果输入a=1,b=2,则输出的a的值为_______.
三、解答题:本大题共6小题,共70分.
17.(
12分)
已知复数(x-2)+(-3x+2)i(x∈R)是4-20i的共轭复数,求x的值.
18.(10分)求证:一个三角形中,最大的角不小于600..
19.(12分)设a,b,c为正数,求证:++≥a+b+c.
20.(12分)某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意度进行调查,并随机抽取了其中30名员工(16名女员工,14名男员工)的得分,如下表:
女
47
36
32
48
34
44
43
47
46
41
43
42
50
43
35
49
男
37
35
34
43
46
36
38
40
39
32
48
33
40
34
(1)根据以上数据,估计该企业得分大于45分的员工人数;
(2)现用计算器求得这30名员工的平均得分为40.5分,若规定大于平均得分为“满意”,否则为“不满意”,请完成下列表格:
“满意”的人数
“不满意”的人数
总计
女
16
男
14
总计
30
(3)根据上述表中数据,利用独立性检验的方法判断,能否有99%的把握认为该企业员工“性别”与“工作是否满意”有关?
21.
(12分)求直线和直线的交点的坐标,及点与的距离。
(12分)在椭圆上找一点,使这一点到直线的距离的最小值。
答案
一.选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
B
D
B
D
B
C
A
C
C
A
.二.填空题(共4小题)
13.9
14. 4
15.
16.
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题12分)
已知复数+x-2+(-3x+2)i(x∈R)是4-20i的共轭复数,求x的值.
解:因为复数4-20i的共轭复数为4+20i,由题意得x2+x-2+(x2-3x+2)i=4+20i,根据复数相等的定义,得方程①的解为x=-3或x=2,方程②的解为x=-3或x=6,所以x=-3.
18.(本小题10分)求证:一个三角形中,最大的角不小于600..
答案在选修1-2
的58页
19.(本小题12分)设a,b,c为正数,
求证:++≥a+b+c.
证明:∵a,b,c均是正数,
∴,,均是正数,
∴+≥2c,+≥2a,+≥2b.
三式相加,得2(++)≥2(a+b+c),∴++≥a+b+c.
20.(本小题12分)某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意度进行调查,并随机抽取了其中30名员工(16名女员工,14名男员工)的得分,如下表:
女
47
36
32
48
34
44
43
47
46
41
43
42
50
43
35
49
男
37
35
34
43
46
36
38
40
39
32
48
33
40
34
(1)根据以上数据,估计该企业得分大于45分的员工人数;
(2)现用计算器求得这30名员工的平均得分为40.5分,若规定大于平均得分为“满意”,否则为“不满意”,请完成下列表格:
“满意”的人数
“不满意”的人数
总计
女
16
男
14
总计
30
(3)根据上述表中数据,利用独立性检验的方法判断,能否有99%的把握认为该企业员工“性别”与“工作是否满意”有关?
解 (1)从表中可知,30名员工中有8名得分大于45分,
所以任选一名员工,他(她)的得分大于45分的概率是=,所以估计此次调查中,该单位约有900×=240名员工的得分大于45分.
(2)由题意可得下列表格:
“满意”的人数
“不满意”的人数
总计
女
12
4
16
男
3
11
14
总计
15
15
30
(3)假设H0:“性别”与“工作是否满意”无关,
根据表中数据,求得χ2=≈8.571>6.635,
所以有99%的把握认为“性别”与“工作是否满意”有关.
21.
(本小题12分)求直线和直线的交点的坐标,及点与的距离。
将代入得,
得,而,得
22.
(本小题12分)在椭圆上找一点,使这一点到直线的距离的最小值。
解:设椭圆的参数方程为,
当时,,此时所求点为。
同课章节目录
