数学六年级下人教版4.2比例的基本性质课件(72张)
文档属性
| 名称 | 数学六年级下人教版4.2比例的基本性质课件(72张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-17 09:58:29 | ||
图片预览





文档简介
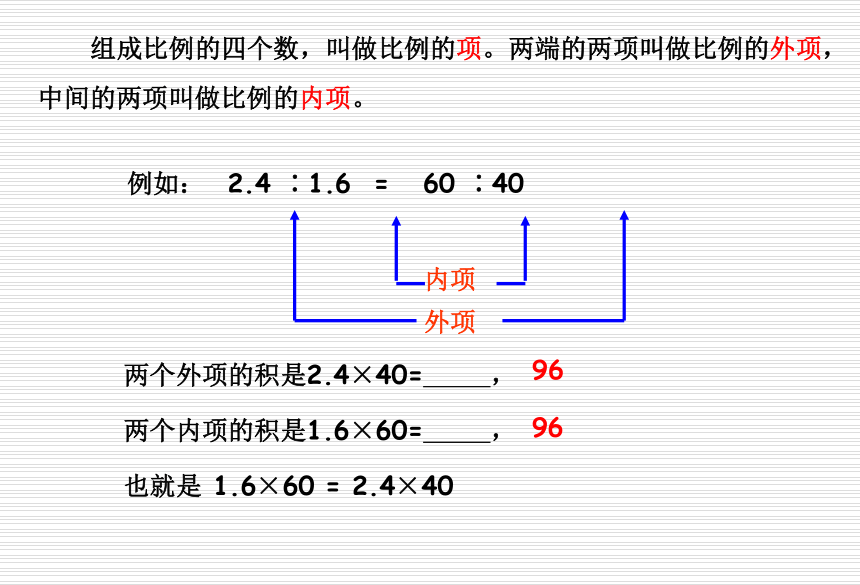
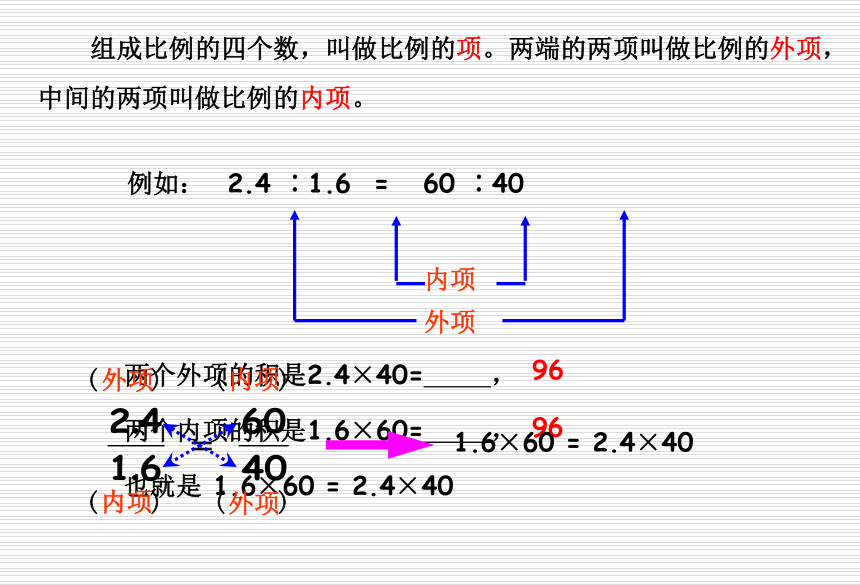
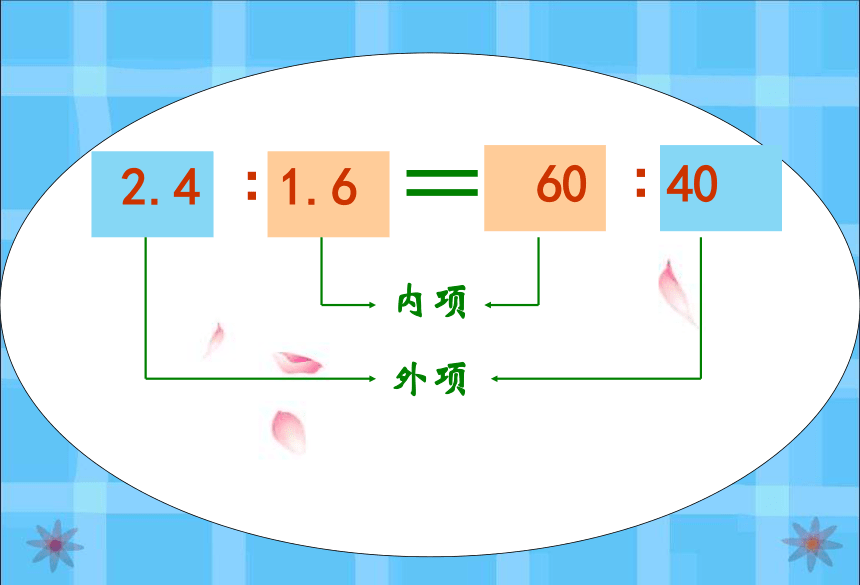
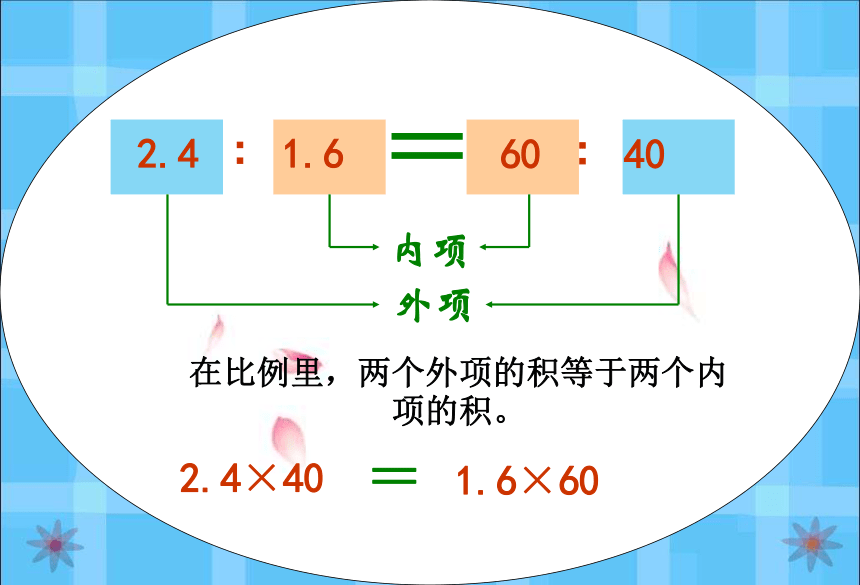
课件72张PPT。比例的基本性质2︰805︰20080︰2200︰5==例如: 2.4 ∶1.6 = 60 ∶40外项内项 组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。两个外项的积是2.4×40= ,两个内项的积是1.6×60= ,9696也就是 1.6×60 = 2.4×40例如: 2.4 ∶1.6 = 60 ∶40外项内项 组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。( )内项( )( )( )外项外项内项1.6×60 = 2.4×40 2.4∶1.6 = 60∶401.6×60 = 2.4×40在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。 如果用字母表示比例的四个项,即 a:b=c:d, 那么比例的基本性质这个可
以表示成:
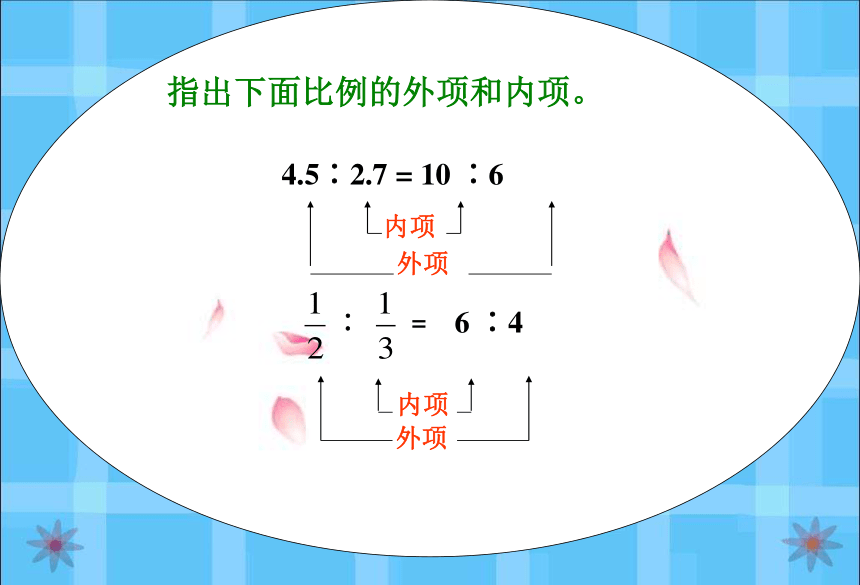
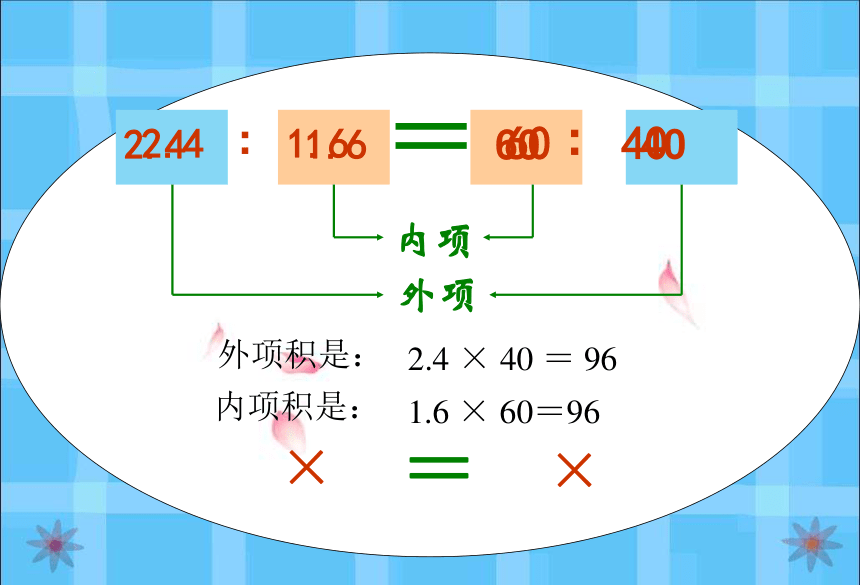
ad=bc 或 bc=ad 0 :0 = 0 :0 如果比例写成分数形式,那些数的乘积相等呢?3×4=2×6 2.4 ︰1.660 ︰40=内项外项 指出下面比例的外项和内项。4.5∶2.7 = 10 ∶6外项外项内项内项 内项积是:1.6 × 60=96外项积是:2.4 × 40 = 962.4401.660××= =2.4×401.6×60在比例里,两个外项的积等于两个内项的积。 2.4︰1.660︰40=外项外项内项内项交叉相乘=2.4×401.6×60 2.4 ︰1.660︰40=在比例里,两个外项的积等于两个
内项的积,这叫做比例的基本性质.比例的基本性质.0.5×2 =( )×( )× =( )×( )25348︰25=40︰125( )×( ) =( )×( )50.281252540 应用比例的基本性质,判断下面两个比能不能组成比例.6∶3 和 8∶5 因为: 6 × 5 = 30
3 × 8 = 24 所以: 6∶3 和 8∶5
不能组成比例.72 ≠ 81 0.2∶2.5 和 4∶50 因为 0.2 × 50 = 10
2.5 × 4 = 10 所以 0.2∶2.5 和4∶50
能组成比例.10 = 10∶ 和 ∶ 因为: × =
× = 所以: ∶ = ∶
能组成比例. = 1.2∶ 和 ∶5 因为: 1.2 × 5 = 6
× = 所以: 1.2∶ 和 ∶5
不能组成比例.6 ≠ 根据上面的等式,你能判断哪两个是外项?哪两个是内项吗?3×4 = 2×6 根据比例的基本性质我们知道,两个内项的积等于两个外项的积。倒过来理解,乘积相等(并且不为0)的两个乘法式子,也可以改写成比例。 根据上面的等式,你能判断哪两个是外项?哪两个是内项吗?3×4 = 2×6你能把上面的等式改写成比例吗?3:2=6:44:2=6:34:6=2:33:6=2:42:3=4:66:3=4:26:4=3:22:4=3:63和4当内项6和2当内项
如果a×2=b×4,则a:b=( ): ( ),如果a:b=4:2,则a =4, b=2,这种说法对吗?为什么?那么a、 b还可能是多少?你发现了什么?
猜猜我是谁?
6 :( )=5 : 4
12:( ) =( ) : 2
不能组成比例。3、2、5、6小游戏:任意说出四个10以内的自然数,
看看它们能不能组成比例。能组成
比例。小游戏:任意说出四个10以内的自然数,
看看它们能不能组成比例。如果把3、40看作外项 3∶8=15 ∶40 3∶15 =8∶40 40∶8=15 ∶3??? 40∶15 =8∶3
如果把3、40看作内项 8∶3=40∶15??? 8∶40=3∶15??????
15∶3=40∶8 15∶40=3∶8 根据上面的等式,你能判断哪两个是外项?哪两个是内项吗?3×40 = 20×6你能把上面的等式改写成比例吗?3:20=6:4040:20=6:340:6=20:33:6=20:4020:3=40:66:3=40:206:40=3:2020:40=3:63和40当内项6和20当内项9 3 5 5 3 C B 下面四个数可以组成比
例,把组成的比例写出来。
3、8、15和40
如果把3、40看作外项 3∶8=15 ∶40 3∶15 =8∶40 40∶8=15 ∶3??? 40∶15 =8∶3
如果把3、40看作内项 8∶3=40∶15??? 8∶40=3∶15??????
15∶3=40∶8 15∶40=3∶8(错)(对)(错)(对)B C B A 9 3 5 5 3 5.下面每组中的四个数都可以组成
比例,把组成的比例写出来:
(1)4、5、12和15。
(2)2、4 、5和10。复习:3、判断下面每组中的两个比能否组成比例?(2) 0.5 : 0.4 和 2 : 2.5根据比例的意义判断:根据比例的基本性质判断:思考 下面的四个数可以组成比例吗?把组成的比例
写出来(能写几个写几个).2、3、4 和 62 ∶3 = 4 ∶62 ∶4 = 3 ∶66 ∶4 = 3 ∶26 ∶3 = 4 ∶24 ∶2 = 6 ∶34 ∶6 = 2 ∶33 ∶6 = 2 ∶43 ∶2 = 6 ∶4
6∶10 和 9∶1520∶5 和 1∶4验证如果把比例写成分数形式,那些数的乘积相等呢?3×4=2×6思考题在一个比例中,两个外项正好互为倒数,已知一个内项是 ,另一个内项是( )根据比例的基本性质,在括号里填上合适的数。做一做 应用比例的基本性质,判断下面哪组中的两个比
可以组成比例.6∶3 和 8∶50.2∶2.5 和 4∶50 因为: 6 × 5 = 30
3 × 8 = 24 所以: 6∶3 和 8∶5
不能组成比例. 因为: 0.2 × 50 = 10
2.5 × 4 = 10 所以:0.2∶2.5 = 4∶50 10 = 10复习:1、什么叫做比例?表示两个比相等的式子叫做比例。2、比和比例有什么区别和联系?填空1 : 2 = 3 : ( )3 : 2 = 6 : ( )5 : 3 = ( ) : ( )( ) : 4 = 6 : ( )6415用四个数3、4、6、8,能组成哪些比例?如:3︰4=6︰8
3︰6=4︰8
4︰8=3︰68︰4=6︰3
6︰3=8︰48︰6=4︰3
4︰3=8︰66︰8=3︰4
合作讨论2:
1、观察比例的两个外项与两个内项,用算一算的方法,找同 学说说你发现了什么?
2、如果把比例写成分数形式,是否也有这样的规律?
3、是不是每一个比例的两个外项与两个内项都具有这种规律,多找几个比例来试一试。
4、通过以上研究你发现了什么?1 在( )里填上合适的数。
5 : 15 = 10 : ( )
16 : 2 =( ) : 0.6
: 0.5 =( ) : ( )
( ) : 6 = 10 : ( )
2 写出比值是0.2的两个比并组成比例。304.83 根据12×0.6=1.8 × 4写出不同的比例。
4 3 、4 、 6 、8 这四个数能组成比例吗? 如果能,请把组成的比例写出来。课外练习把下面的等式改写成比例。 (1)3×40=8×15 (2)5×A=9×B (3)ac=bd复习:3、判断下面每组中的两个比能否组成比例?(1) 6:15 和 8:20根据比例的意义判断。复习:3、判断下面每组中的两个比能否组成比例?(2) 0.5 : 0.4 和 2 : 2.5根据比例的意义判断。例如: 2.4 ∶1.6 = 60 ∶40外项内项 组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。两个外项的积是2.4×40= ,两个内项的积是1.6×60= ,9696也就是 1.6×60 = 2.4×40例如: 2.4 ∶1.6 = 60 ∶40外项内项 组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。( )内项( )( )( )外项外项内项1.6×60 = 2.4×40 2.4∶1.6 = 60∶401.6×60 = 2.4×40在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。复习:3、判断下面每组中的两个比能否组成比例?(1) 6:15 和 8:20根据比例的意义判断:根据比例的基本性质判断:复习:3、判断下面每组中的两个比能否组成比例?(2) 0.5 : 0.4 和 2 : 2.5根据比例的意义判断:根据比例的基本性质判断: 根据上面的等式,你能判断哪两个是外项?哪两个是内项吗?3×40 = 20×6 根据比例的基本性质我们知道,两个内项的积等于两个外项的积。倒过来理解,乘积相等(并且不为0)的两个乘法式子,也可以改写成比例。 应用比例的基本性质,判断下面哪组中的两个比
可以组成比例。6∶3和8∶50.2∶2.5和4∶50 因为 6×5=30 所以 6∶3和8∶5不能
组成比例. 所以 0.2∶2.5 =4∶50 10=103×8=2430≠24 因为 2.5×4=100.2×50=10 应用比例的基本性质,判断下面哪组中的两个比
可以组成比例。7、9a、b632419 5
33
52、判断。
(1)在比例中,两个外项的积减去两个
内项的积,差是0。( )
(2)18:30和3:5可以组成比例。( )
(3)如果4X=3Y,(X和Y均不为0),
那么4:X=3:Y。( )
(4)因为3×10=5×6,所以3:5=10:6。( )√√××练习六12:16 = 3:4思考题在一个比例中,两个外项正好互为倒数,已知一个内项是 ,另一个内项是( )只会在水泥地上走路的人,
永远不会留下深深的脚印。 数学故事 不久前,马惠惠家的菜地边高高矗立起一个新铁塔。这天午后,阳光明媚,邻居家刚读一年级的小明又拉着马惠惠来到铁塔下。玩着玩着,小明问道:“惠惠姐,这铁塔干嘛用?”“铁塔嘛,架设高压线用的,以后电线架好了,就不能来玩了,也不能攀登了,高压线可危险啦!”“那这个铁塔有多高呀?”马惠惠想了想,便跑回家,拿了一根2米长的竹竿和一把卷尺,在地上量了起来,才一会儿,她就自信的告诉小明:“铁塔有15米高。”铁塔高:?米 影子长6米
竹竿长:2米 影子长0.8米2 : 0.8 = X : 6
以表示成:
ad=bc 或 bc=ad 0 :0 = 0 :0 如果比例写成分数形式,那些数的乘积相等呢?3×4=2×6 2.4 ︰1.660 ︰40=内项外项 指出下面比例的外项和内项。4.5∶2.7 = 10 ∶6外项外项内项内项 内项积是:1.6 × 60=96外项积是:2.4 × 40 = 962.4401.660××= =2.4×401.6×60在比例里,两个外项的积等于两个内项的积。 2.4︰1.660︰40=外项外项内项内项交叉相乘=2.4×401.6×60 2.4 ︰1.660︰40=在比例里,两个外项的积等于两个
内项的积,这叫做比例的基本性质.比例的基本性质.0.5×2 =( )×( )× =( )×( )25348︰25=40︰125( )×( ) =( )×( )50.281252540 应用比例的基本性质,判断下面两个比能不能组成比例.6∶3 和 8∶5 因为: 6 × 5 = 30
3 × 8 = 24 所以: 6∶3 和 8∶5
不能组成比例.72 ≠ 81 0.2∶2.5 和 4∶50 因为 0.2 × 50 = 10
2.5 × 4 = 10 所以 0.2∶2.5 和4∶50
能组成比例.10 = 10∶ 和 ∶ 因为: × =
× = 所以: ∶ = ∶
能组成比例. = 1.2∶ 和 ∶5 因为: 1.2 × 5 = 6
× = 所以: 1.2∶ 和 ∶5
不能组成比例.6 ≠ 根据上面的等式,你能判断哪两个是外项?哪两个是内项吗?3×4 = 2×6 根据比例的基本性质我们知道,两个内项的积等于两个外项的积。倒过来理解,乘积相等(并且不为0)的两个乘法式子,也可以改写成比例。 根据上面的等式,你能判断哪两个是外项?哪两个是内项吗?3×4 = 2×6你能把上面的等式改写成比例吗?3:2=6:44:2=6:34:6=2:33:6=2:42:3=4:66:3=4:26:4=3:22:4=3:63和4当内项6和2当内项
如果a×2=b×4,则a:b=( ): ( ),如果a:b=4:2,则a =4, b=2,这种说法对吗?为什么?那么a、 b还可能是多少?你发现了什么?
猜猜我是谁?
6 :( )=5 : 4
12:( ) =( ) : 2
不能组成比例。3、2、5、6小游戏:任意说出四个10以内的自然数,
看看它们能不能组成比例。能组成
比例。小游戏:任意说出四个10以内的自然数,
看看它们能不能组成比例。如果把3、40看作外项 3∶8=15 ∶40 3∶15 =8∶40 40∶8=15 ∶3??? 40∶15 =8∶3
如果把3、40看作内项 8∶3=40∶15??? 8∶40=3∶15??????
15∶3=40∶8 15∶40=3∶8 根据上面的等式,你能判断哪两个是外项?哪两个是内项吗?3×40 = 20×6你能把上面的等式改写成比例吗?3:20=6:4040:20=6:340:6=20:33:6=20:4020:3=40:66:3=40:206:40=3:2020:40=3:63和40当内项6和20当内项9 3 5 5 3 C B 下面四个数可以组成比
例,把组成的比例写出来。
3、8、15和40
如果把3、40看作外项 3∶8=15 ∶40 3∶15 =8∶40 40∶8=15 ∶3??? 40∶15 =8∶3
如果把3、40看作内项 8∶3=40∶15??? 8∶40=3∶15??????
15∶3=40∶8 15∶40=3∶8(错)(对)(错)(对)B C B A 9 3 5 5 3 5.下面每组中的四个数都可以组成
比例,把组成的比例写出来:
(1)4、5、12和15。
(2)2、4 、5和10。复习:3、判断下面每组中的两个比能否组成比例?(2) 0.5 : 0.4 和 2 : 2.5根据比例的意义判断:根据比例的基本性质判断:思考 下面的四个数可以组成比例吗?把组成的比例
写出来(能写几个写几个).2、3、4 和 62 ∶3 = 4 ∶62 ∶4 = 3 ∶66 ∶4 = 3 ∶26 ∶3 = 4 ∶24 ∶2 = 6 ∶34 ∶6 = 2 ∶33 ∶6 = 2 ∶43 ∶2 = 6 ∶4
6∶10 和 9∶1520∶5 和 1∶4验证如果把比例写成分数形式,那些数的乘积相等呢?3×4=2×6思考题在一个比例中,两个外项正好互为倒数,已知一个内项是 ,另一个内项是( )根据比例的基本性质,在括号里填上合适的数。做一做 应用比例的基本性质,判断下面哪组中的两个比
可以组成比例.6∶3 和 8∶50.2∶2.5 和 4∶50 因为: 6 × 5 = 30
3 × 8 = 24 所以: 6∶3 和 8∶5
不能组成比例. 因为: 0.2 × 50 = 10
2.5 × 4 = 10 所以:0.2∶2.5 = 4∶50 10 = 10复习:1、什么叫做比例?表示两个比相等的式子叫做比例。2、比和比例有什么区别和联系?填空1 : 2 = 3 : ( )3 : 2 = 6 : ( )5 : 3 = ( ) : ( )( ) : 4 = 6 : ( )6415用四个数3、4、6、8,能组成哪些比例?如:3︰4=6︰8
3︰6=4︰8
4︰8=3︰68︰4=6︰3
6︰3=8︰48︰6=4︰3
4︰3=8︰66︰8=3︰4
合作讨论2:
1、观察比例的两个外项与两个内项,用算一算的方法,找同 学说说你发现了什么?
2、如果把比例写成分数形式,是否也有这样的规律?
3、是不是每一个比例的两个外项与两个内项都具有这种规律,多找几个比例来试一试。
4、通过以上研究你发现了什么?1 在( )里填上合适的数。
5 : 15 = 10 : ( )
16 : 2 =( ) : 0.6
: 0.5 =( ) : ( )
( ) : 6 = 10 : ( )
2 写出比值是0.2的两个比并组成比例。304.83 根据12×0.6=1.8 × 4写出不同的比例。
4 3 、4 、 6 、8 这四个数能组成比例吗? 如果能,请把组成的比例写出来。课外练习把下面的等式改写成比例。 (1)3×40=8×15 (2)5×A=9×B (3)ac=bd复习:3、判断下面每组中的两个比能否组成比例?(1) 6:15 和 8:20根据比例的意义判断。复习:3、判断下面每组中的两个比能否组成比例?(2) 0.5 : 0.4 和 2 : 2.5根据比例的意义判断。例如: 2.4 ∶1.6 = 60 ∶40外项内项 组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。两个外项的积是2.4×40= ,两个内项的积是1.6×60= ,9696也就是 1.6×60 = 2.4×40例如: 2.4 ∶1.6 = 60 ∶40外项内项 组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。( )内项( )( )( )外项外项内项1.6×60 = 2.4×40 2.4∶1.6 = 60∶401.6×60 = 2.4×40在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。复习:3、判断下面每组中的两个比能否组成比例?(1) 6:15 和 8:20根据比例的意义判断:根据比例的基本性质判断:复习:3、判断下面每组中的两个比能否组成比例?(2) 0.5 : 0.4 和 2 : 2.5根据比例的意义判断:根据比例的基本性质判断: 根据上面的等式,你能判断哪两个是外项?哪两个是内项吗?3×40 = 20×6 根据比例的基本性质我们知道,两个内项的积等于两个外项的积。倒过来理解,乘积相等(并且不为0)的两个乘法式子,也可以改写成比例。 应用比例的基本性质,判断下面哪组中的两个比
可以组成比例。6∶3和8∶50.2∶2.5和4∶50 因为 6×5=30 所以 6∶3和8∶5不能
组成比例. 所以 0.2∶2.5 =4∶50 10=103×8=2430≠24 因为 2.5×4=100.2×50=10 应用比例的基本性质,判断下面哪组中的两个比
可以组成比例。7、9a、b632419 5
33
52、判断。
(1)在比例中,两个外项的积减去两个
内项的积,差是0。( )
(2)18:30和3:5可以组成比例。( )
(3)如果4X=3Y,(X和Y均不为0),
那么4:X=3:Y。( )
(4)因为3×10=5×6,所以3:5=10:6。( )√√××练习六12:16 = 3:4思考题在一个比例中,两个外项正好互为倒数,已知一个内项是 ,另一个内项是( )只会在水泥地上走路的人,
永远不会留下深深的脚印。 数学故事 不久前,马惠惠家的菜地边高高矗立起一个新铁塔。这天午后,阳光明媚,邻居家刚读一年级的小明又拉着马惠惠来到铁塔下。玩着玩着,小明问道:“惠惠姐,这铁塔干嘛用?”“铁塔嘛,架设高压线用的,以后电线架好了,就不能来玩了,也不能攀登了,高压线可危险啦!”“那这个铁塔有多高呀?”马惠惠想了想,便跑回家,拿了一根2米长的竹竿和一把卷尺,在地上量了起来,才一会儿,她就自信的告诉小明:“铁塔有15米高。”铁塔高:?米 影子长6米
竹竿长:2米 影子长0.8米2 : 0.8 = X : 6
