数学六年级下人教版总复习6.1数的认识课件(50张)
文档属性
| 名称 | 数学六年级下人教版总复习6.1数的认识课件(50张) |  | |
| 格式 | zip | ||
| 文件大小 | 460.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-17 10:55:49 | ||
图片预览










文档简介
课件50张PPT。小学数学毕业总复习数的认识一、数的认识
一块蛋糕为5.8元1,2,3,4,‥‥‥中国的国土面积约是9600000平方千米。北极地区的多数地区为冰雪覆盖,冬季冰雪覆盖面积为73%,夏季为53%。
今年我市空气质量良好的天数占全年天数的3/5。上面都使用了哪种数,你知道它们的含义吗?数物体的时候,用来表示物体个数的数叫做自然数. (象0,1,2,3…)
数1、整数
2、小数
3、分数
4、百分数(成数、折扣)正整数
0
负整数
自然数0的作用:
1、表示“没有” 2、表示“起点”
3、表示“占位” 4、表示“分界”0是最小的自然数。自然数的计数单位是“1”.1、十进制计数法 一(个)、十、百、千、万……都叫做计数单位.其中“一”是计数的基本单位.
10个一是十,10个十是百……10个一百亿是一千亿……每相邻两个计数单位之间的进率都是10.这种计数方法叫做十进制计数法.
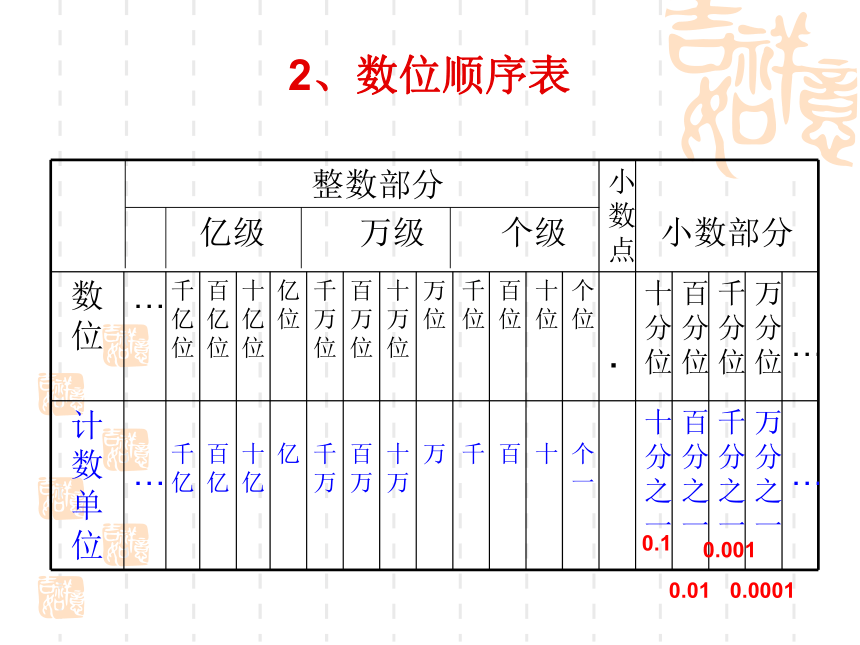
2、数位顺序表0.10.010.0010.00013、整数的读法和写法 读数时,从高位起,一级一级地往下读,属于亿级和万级的要读出级名.
读数时,每级末尾的“0”都不读,其他数位有一个0或连续几个0都只读一个0.
8000406000读作: 写数时,从高位起,一级一级地往下写,哪一位上一个单位也没有,就在哪个数位上写0六亿八千四百五十二万八千五百六十三.684528563读作:八十亿零四十万六千.
四十亿六千零六十万零五十写作:40606000504、改写与省略的对比5、数的改写 一个较大的多位数,为了读写方便,常常把它改写成用
“万”或“亿”作单位的数.有时还可以根据需要,省略这个数某
一位后面的尾数,写成近似数.
把76450000改写成用“万”作单位的数是( )
把235800改写成用“万”作单位的数是( )
235800省略万位后面的尾数约为( )
把34562800000改写成用“亿”作单位的数后,保留两位
小数是( )
4.62975保留两位小数是:( )
4.62975保留三位小数是:( )=7645万=23.58万≈ 24万≈ 345.63亿 ≈ 4.63≈ 4.630(改写成用“万”作单位时,在万位右下角点上“.”,加上“万”字;改写成用“亿”作单位时,在亿位右下角点上“.”,加上“亿”字。)
6、整数大小1、比较两个多位数的大小,首先看它们位数的多少,位数较多的数较大;
如:9998( )10000<2、如果两个数的位数相同,那么首先看最高位,最高 位上的数较大的,这个数就大;如果最高位相同,则左边第二位上的数较大的,这个数就大……
如:34021( )31782>3、最大一位数是9;最大两位数是99;最大三位数是999…最小一位数是1;最小两位数是10;最小三位数是100…
7、小数 把整体(单位)“1”平均分成10份,100份……这样的一份或几份分别是十分之几,百分之几……可以用小数表示.
小数点右边第一位是( ),计数单位是( );第二位是( ),计数单位是( )……
小数部分的最大计数单位是( ), ( )最小的计数单位.
小数部分有几位,就叫做几位小数. 十分位十分之一百分位百分之一十分之一没有8、小数的分类小数有限小数
无限小数循环小数
无限不循环小数
纯循环小数
混循环小数小数纯小数
带小数
(1).按小数位数是有限还是无限分(2).按小数的整数部分是否为0分9、小数的读法和写法 读小数时,小数的整数部分按整数的读法来读,小数点读作“点”,小数部分按照顺序读出每一个数位上的数字.
写小数时,整数部分按照整数的写法来写,小数点写在个位右下角,小数部分顺次写出每一个数位上的数字. 如 45.469 读作:四十五点四六九10、小数的性质 小数的末尾添上0或者去掉0,小数的大小不变.
运用小数的性质,可以在小数末尾添上0或去掉0.
3.5=3.50 21.06=21.06000 ...也可以把小数化简.
3.500=3.5 4.0030=4.003 ...11、小数点位置移动引起小数大小的变化 小数点向右(左)移动一位、两位、三位……原来的数就扩大(缩小)10倍、100倍、1000倍……
如果要把一个数扩大或缩小10倍、100倍……只需要移动小数点,数位不够时用0补足.12、循环小数1、一个小数的小数部分,从某一位起,有一个或几个数字依次不断重复出现,这样的数叫做循环小数.
如 0.5555…… 7.23838……
2、依次不断重复出现的数字叫做循环节.
3、循环小数的简便记法:
(在第一个循环节上面点一点或点两点.)
0.5555…记作:...12.412412…记作:12.412. .0.57.23838…记作:7.238
13.循环小数 循环节从小数部分第一位开始的叫纯循环小数
如: 0.5
循环节不是从小数部分第一位开始的叫混循环小数.
如:7.238...14、四舍五入法 求一个数的近似数,要看尾数的最高位上的数是几,如果比5小,就把尾数都舍去;如果尾数最高位上的数是5或大于5,就把尾数舍去后,要向它的前一位进1.
随堂练习填空
1、最小的自然数是( ),最小的一位数是( )。
2、把637000000改写成用“亿”作单位的数是( ),省略“亿”后面的尾数是( )。
3、7.85中7表示( ),8表示( ),5表示( )。
4、一个两位小数,四舍五入的值是3.9,这个两位小数最大是( ),最小是( )。
5、9.5的计数单位是( ),9.50的计数单位是( )。
6、3.046精确到十分位是( ),精确到百分位是( )。
7、如果一个四位小数精确到百分位是5.30,这个四位小数最大是( ),最小是( )。5.30495.295015、分数的意义和分数单位单位“1”----一个物体,一个计量单位或是许多物体组成的一个整体,都可以用自然数1来表示,通常我们把它叫做单位“1”分 数----分数各部分的名称:分数单位----把单位“1”平均分成若干份,表示其中的一份的数.(表示平均分的份数)(表示所取的份数)把单位“1”平均分成若干份,表示这样的一份或者几份的数,叫做分数.16、分数的分类真分数----
如:
假分数----分子比分母小的分数.分子比分母大或者分子和分母
相等的分数.真分数 < 1假分数 ≥ 15 13
6 29
如: 13 25
9 1817、分数与除法分数与除法的关系:被除数÷除数=(除数≠0)把单位“1”平均分成( )份,取其中的( )份. 把5平均分成9份,取其中的( ),
用字母表示:951份18、分数大小的比较★分母相同的两个分数,分子大的分数比较大.★分子相同的两个分数,分母小的分数比较大.<><>★分子分母不同的两个分数,先通分, 求出原来几个分母的最小公倍数,然后把各个分数分别化成用这个最小公倍数作分母的分数.<19、分数的基本性质 分数的分子和分母同时 乘或者除以相同的数
(零除外),分数的大小不变.一个分数:
如果分母不变,分子乘以3,则这个分数( )
如果分子不变,分母除以3,则这个分数( )扩大3倍扩大3倍如: 3
43×6
4×6==18
2427
48=27÷3
48÷3=9
1620、最简分数*计算结果,能约分的要约分,一般要约成最简分数;假分数的,一般要化成带分数或整数.*判断一个最简分数能不能化成有限小数:分母中除了2和5以外,不含有其他的质因数,就能化成有限小数.√××
√√√*分子分母是互质数的分数——叫最简分数如:21、约分约分------把一个分数化成和它相等,但分子和分母
都比较小的分数.约分的方法:
1.用分子分母的公因数(1除外)依次去除分子和分母,直至得到分子分母是互质数的最简分数为止.
2.或者用分子和分母的最大公因数去除分子和分母.随堂练习
1、5/8表示把单位“1”平均分成( )份,取其中的( )份,它还表示把( )平均分成( ),其中的( )份是多少。
2、把4吨化肥平均分给5户农民,平均每户农民分得这些化肥的( ),每户分得( )吨。
3、把5/12的分母加上36,要使分数的大小不变,分子应加上( )。
4、当a( )时,8/a是真分数,当a( )时,8/a是假分数。
5、5/9千米表示1千米的( ),也可以表示( )千米的1/9。
6、把2米长的绳子平均分成7份,每份长( )米,每份占全长的( )。
7、分母是8的最简真分数的和是( )。
8、比7/8小且比5/8大的分数有( )个。22、百分数的意义表示一个数是另一个数的百分之几的数叫百分数.
百分数又叫百分率或百分比.你能在下面的数轴上给这些车找到停车位吗?0.57/103.56/23/32-2.5
结合实例说一说分数和百分数有什么联系和区别?分数:既可以表示一个数,又可以表示两个数的比。
百分数:只表示两个数的比。百分数的分母固定是100,通常不写成分数形式,写成( )%,不能带单位。百分数的分子可以小于100,也可以大于等于100,可以是整数,也可以是小数。23、分数、小数、百分数的互化小数分 数百分数0.25=( )小数点向右移动两位,添上%0.35%=( )去掉%,小数点向左移动两位先化成小数,再化成百分数先写成分数,再约分先用分数表示,再约分分子除以分母=40%=2
51
6≈0.167=16.7%1
4=1÷4=0.251.2=25%0.0035二、数的整除
1. 整除与除尽
2. 因数和倍数
3. 能被2.3.5整除的数的特征
4. 偶数和奇数
5. 质数和合数
6. 质因数和分解质因数
7. 最大公因数和最小公倍数1. 整除与除尽★整除:整数a除以整数b(b≠0),除得的商是整数而没有余数,我们就说数a能被数b整除,或数b能整除a.★除尽:数a除以数b(b≠0),除得的商是整数或是有限小数,
这就叫做除尽.整除是除尽的一种特殊情况,整除也可以说是除尽,
但除尽不一定是整除.★区别:如:12÷4=3我们就说:12能被4整除;或者说4能整除12.(即:商可以是小数)如:5÷8=0.625(我们不能说5能被8整除,只能说5能被8除尽。)2. 因数和倍数如果数a能被数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数.一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身.一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数.
因数和倍数是相互依存的。不能只说某个数是倍数,某个数是因数。
如:12÷4=312就叫做4的倍数,4就叫做12的因数.
如:12是倍数,
4是因数…都是错的。3. 能被2.3.5整除的数的特征★能被2整除的数的特征:
★能被5整除的数的特征:
★能被3整除的数的特征:
个位上是0,2,4,6,8。个位上是0或5。 各个数位上的数字之和能被3整除。★能同时被2,5整除的数的特征:个位是0。★能同时被2,3,5整除的数的特征:个位是0,而且各个数位上的
数字之和能被3整除.★注意:
有一些数能被7,9,11,13整除,但是不容易看出来,
这是大家在约分中容易忽略的,平时练习中要多注意。4. 偶数和奇数一个自然数,不是奇数就是偶数。偶数:能被2整除的数叫做偶数。奇数:不能被2整除的数叫做奇数。偶数±偶数=( )偶数×偶数=( )偶数偶数偶数偶数奇数奇数★最小的偶数是:★最小的奇数是:01奇数±奇数=( )偶数±奇数=( )
奇数×奇数=( )偶数×奇数=( )
5. 质数和合数质数(素数):只有1和它本身两个因数的数。合数:除了1和它本身还有别的因数的数。1: 既不是质数也不是合数。最小的质数是:最小的合数是:246. 质因数和分解质因数质因数:分解质因数:每一个合数都可以写成几个质数相乘的形式,
这几个质数叫做这个合数的质因数.把一个合数用几个质因数相乘的形式表示出来.
叫做分解质因数. 分解质因数的方法:短除法302153530=2×3×5★ 把30分解质因数不能写成:2×3×5=30也不能写成: 30=1×2 ×3 ×5
因为1不是质数7. 最大公因数(公约数)和最小公倍数
1、公因数(公约数):其中最大的一个叫做这几个数的最大公因(约)数.
例:8和12的公因(约)数有( ),( )是8和12的最大公因数.1、2、443、公倍数:几个数公有的倍数,叫做这几个数的公倍数,
例:4和6的公倍数有( ),( )是4和6的最小公倍数.
12、24、36…125、互质数:公因(约)数只有1的两个数叫做互质数.⑴、两个数都是质数,这两个数一定互质数. 如:9和13
⑵、相邻的两个自然数一定互质数. 如:15和16
⑶、相邻的两个奇数一定互质数. 如:25和27
(4)、1和任何自然数都是互质数. 如:1和20
(5)、两个数都是合数也有可能是互质数。 如:8和156、互质数的几种特殊情况:2、最大公因(约)数:几个数公有的因数,叫做这几个数的公因(约)数;
(公倍数没有最大的)4、最小公倍数:其中最小的一个叫做这几个数的最小公倍数.
8、求最大公因(约)数和最小公倍数如:4和28 最大公因数是( ); 最小公倍数是( )。
★如果较小数是较大数的因数:
较小数就是这两个数的最大公因(约)数;
较大数就是这两个数的最小公倍数.如:4和15 最大公因数是( ); 最小公倍数是( )。★如果两个数是互质数:
它们的最大公因数就是1;
最小公倍数就是它们的乘积.42816024 362121826932324和36的最大公因数是:2×2×3=1224和36的最小公倍数是: 2×2×3×2×3=72除到商是互质数为止除数相乘所有的除数和商相乘如:求24和36的最大公因数和最小公倍数9、用短除法求最大公因数和最小公倍数一般用质数除。随堂练习判断:
1、互质的两个数,没有公因数。( )
2、所有自然数,不是奇数就是偶数。( )
3、36÷9=4,所以36是倍数,9是因数。( )
4、一个数的倍数总比这个数的因数大。( )随堂练习1、7□6□既有因数3,同时又是2和5的倍数,这个四位数是( )。
2、两个质数的积,一定是( )。
3、12的因数有( )。
4、若a=8b,(a、b都不为0),则a、b的最大公因数是( ),最小公倍数是( )。
5、相邻两个质数的和最小是( )。
6、在0~20中,奇数有( ),偶数有( ),质数有( ),合数有( ),2的倍数有( ),3的倍数有( ),5的倍数有( )。随堂练习7、A和B都是自然数,且A÷B=7,那么A与B的最大公因数是( ),最小公倍数是( )。
8、A、B两个数分解质因数分别是A=2×3×7,B=2×5×7。A、B的最大公因数是( ),最小公倍数是( )。
9、8个连续自然数的和是284,这8个自然数分别是( )。
10、9个连续偶数的和是90,这9个连续偶数分别是( )。
11、7个连续自然数的和为35,这7个自然数分别是( )。一、用公因数知识解决生活问题。1、用96朵红玫瑰和72朵白玫瑰做成花束。如果每个花束里的红玫瑰和白玫瑰的朵数相同且没有剩余,最多可以做多少个花束?每个花束里至少要有几朵束? 每个花束里的红玫瑰和白玫瑰的朵数相同,又要求花束的个数最多,所以花束的个数应该是96和72的最大公因数。 (96,72)=24
96÷24+72÷24=7(朵)一、用公因数知识解决生活问题。2、将一张长75厘米,宽60厘米的硬纸板剪成多个同样大小的正方形,使得硬纸板没有剩余,并且剪成的正方形的面积尽可能大,一共可以剪几个相同的正方形? 剪同样大小的正方形且没有剩余,则正方形的边长是长和宽的公因数,为使面积最大,正方形的边长应是长和宽的最大公因数。 (75,60)=15
(75÷15)×(60÷15)=20(个) 变一变:将一张长1.36米,宽0.8米的长方形纸片,裁成一样大小的正方形纸片,并使它们的面积尽可能的大表没有剩余,则一共可裁出多少张? (136,80)=8
(136÷8)×(80÷8)=170(个)二、用公倍数知识解决生活问题。1、暑假期间,小明和小兰都去参加游泳训练,8月1日两人同时参加游泳训练后,小明每6天去一次,小兰每8天去一次,那么几月几日两人再次相遇? 由题意可知,两个人要再次相遇,相隔的天数应分别是6的倍数,也是8的倍数,那么相隔的天数应是6和8的最小公倍数。 [ 6,8 ]=24
所以再次相遇应是8月25日。二、用公倍数知识解决生活问题。2、一筐苹果,如果3个3个地数,最后余2个,如果5个5个地数,最后余4个,如果7个7个地数,最后余6个。这筐苹果最少有多少个? 由题意可知,假设再添上1个苹果,则余下的苹果数分别是3、5、7,就正好再数一次,正好数完,也就是总数加上1后是3、5、7的最小公倍数。 [ 3,5,7 ]=105
105-1=104(个) 变一变:有一盒巧克力,7粒7粒地数还余4粒,5粒5粒地数又少3粒,3粒3粒地数正好数完。这盒巧克力至少有多少粒? 由题意可知,如果巧克力再多3粒,就正好是7、5、3的倍数,所以这盒巧克力至少的粒数就是求7、5、3的最少公倍数再减3。
7×5×3-3=102(粒)练习1、体育课上,老师为同学们整队时发现,无论是3人一排,4人一排,还是5人一排都多2个人,如果老师让全班站成两列纵队,每队几个人?(全班不超过100人)
2、有三根铁丝,一根长18米,一根长24米,一根长30米,现在要把它们截成同样长的小段,每段最长几米?一共可以截多少段?
3、一张长42厘米,宽35厘米的长方形纸,把这张纸剪成正方形小纸片。要使小正方形尽可能的大,可剪多少个小正方形?正方形的边长是多少厘米?
4、一堆糖果,如果平均分给4个小朋友,还剩3个;如果平均分给5个小朋友,还缺1个;如果平均分给6个小朋友,也缺1个,这堆糖果至少有多少个?练习5、一个小数的小数点向左移动两位,所得到的新数比原数小3.564,原数是多少?
6、甲数比乙数少34.65,甲数的小数点向右移动一位正好与乙数相等。甲、乙两数各是多少?
7、小明家的电话号码是由7个数字组成的。以下是电话号码ABCDEFG的密码:A减1就是最小的质数;B既是偶数,又是质数;C是最大的一位数;D是2和3的最小公倍数;E是10以内最大的质数;F既不是正数,也不是负数;G是最小的质数减1。小明家的电话号码是多少?10、倒数的认识乘积是1的两个数互为倒数。如: × = 1 和 互为倒数。就是 的倒数是 , 的倒数是 。★互为倒数的两个数是互相依存的,不能只单独说某个数 是倒数。一定要说“谁”是“谁”的倒数。★求一个数(0除外)的倒数,只要把这个数的分子、分母调换位置。分子、分母调换位置12分子、分母调换位置1 的倒数还是( ) ,1 ( )没有倒数。0
一块蛋糕为5.8元1,2,3,4,‥‥‥中国的国土面积约是9600000平方千米。北极地区的多数地区为冰雪覆盖,冬季冰雪覆盖面积为73%,夏季为53%。
今年我市空气质量良好的天数占全年天数的3/5。上面都使用了哪种数,你知道它们的含义吗?数物体的时候,用来表示物体个数的数叫做自然数. (象0,1,2,3…)
数1、整数
2、小数
3、分数
4、百分数(成数、折扣)正整数
0
负整数
自然数0的作用:
1、表示“没有” 2、表示“起点”
3、表示“占位” 4、表示“分界”0是最小的自然数。自然数的计数单位是“1”.1、十进制计数法 一(个)、十、百、千、万……都叫做计数单位.其中“一”是计数的基本单位.
10个一是十,10个十是百……10个一百亿是一千亿……每相邻两个计数单位之间的进率都是10.这种计数方法叫做十进制计数法.
2、数位顺序表0.10.010.0010.00013、整数的读法和写法 读数时,从高位起,一级一级地往下读,属于亿级和万级的要读出级名.
读数时,每级末尾的“0”都不读,其他数位有一个0或连续几个0都只读一个0.
8000406000读作: 写数时,从高位起,一级一级地往下写,哪一位上一个单位也没有,就在哪个数位上写0六亿八千四百五十二万八千五百六十三.684528563读作:八十亿零四十万六千.
四十亿六千零六十万零五十写作:40606000504、改写与省略的对比5、数的改写 一个较大的多位数,为了读写方便,常常把它改写成用
“万”或“亿”作单位的数.有时还可以根据需要,省略这个数某
一位后面的尾数,写成近似数.
把76450000改写成用“万”作单位的数是( )
把235800改写成用“万”作单位的数是( )
235800省略万位后面的尾数约为( )
把34562800000改写成用“亿”作单位的数后,保留两位
小数是( )
4.62975保留两位小数是:( )
4.62975保留三位小数是:( )=7645万=23.58万≈ 24万≈ 345.63亿 ≈ 4.63≈ 4.630(改写成用“万”作单位时,在万位右下角点上“.”,加上“万”字;改写成用“亿”作单位时,在亿位右下角点上“.”,加上“亿”字。)
6、整数大小1、比较两个多位数的大小,首先看它们位数的多少,位数较多的数较大;
如:9998( )10000<2、如果两个数的位数相同,那么首先看最高位,最高 位上的数较大的,这个数就大;如果最高位相同,则左边第二位上的数较大的,这个数就大……
如:34021( )31782>3、最大一位数是9;最大两位数是99;最大三位数是999…最小一位数是1;最小两位数是10;最小三位数是100…
7、小数 把整体(单位)“1”平均分成10份,100份……这样的一份或几份分别是十分之几,百分之几……可以用小数表示.
小数点右边第一位是( ),计数单位是( );第二位是( ),计数单位是( )……
小数部分的最大计数单位是( ), ( )最小的计数单位.
小数部分有几位,就叫做几位小数. 十分位十分之一百分位百分之一十分之一没有8、小数的分类小数有限小数
无限小数循环小数
无限不循环小数
纯循环小数
混循环小数小数纯小数
带小数
(1).按小数位数是有限还是无限分(2).按小数的整数部分是否为0分9、小数的读法和写法 读小数时,小数的整数部分按整数的读法来读,小数点读作“点”,小数部分按照顺序读出每一个数位上的数字.
写小数时,整数部分按照整数的写法来写,小数点写在个位右下角,小数部分顺次写出每一个数位上的数字. 如 45.469 读作:四十五点四六九10、小数的性质 小数的末尾添上0或者去掉0,小数的大小不变.
运用小数的性质,可以在小数末尾添上0或去掉0.
3.5=3.50 21.06=21.06000 ...也可以把小数化简.
3.500=3.5 4.0030=4.003 ...11、小数点位置移动引起小数大小的变化 小数点向右(左)移动一位、两位、三位……原来的数就扩大(缩小)10倍、100倍、1000倍……
如果要把一个数扩大或缩小10倍、100倍……只需要移动小数点,数位不够时用0补足.12、循环小数1、一个小数的小数部分,从某一位起,有一个或几个数字依次不断重复出现,这样的数叫做循环小数.
如 0.5555…… 7.23838……
2、依次不断重复出现的数字叫做循环节.
3、循环小数的简便记法:
(在第一个循环节上面点一点或点两点.)
0.5555…记作:...12.412412…记作:12.412. .0.57.23838…记作:7.238
13.循环小数 循环节从小数部分第一位开始的叫纯循环小数
如: 0.5
循环节不是从小数部分第一位开始的叫混循环小数.
如:7.238...14、四舍五入法 求一个数的近似数,要看尾数的最高位上的数是几,如果比5小,就把尾数都舍去;如果尾数最高位上的数是5或大于5,就把尾数舍去后,要向它的前一位进1.
随堂练习填空
1、最小的自然数是( ),最小的一位数是( )。
2、把637000000改写成用“亿”作单位的数是( ),省略“亿”后面的尾数是( )。
3、7.85中7表示( ),8表示( ),5表示( )。
4、一个两位小数,四舍五入的值是3.9,这个两位小数最大是( ),最小是( )。
5、9.5的计数单位是( ),9.50的计数单位是( )。
6、3.046精确到十分位是( ),精确到百分位是( )。
7、如果一个四位小数精确到百分位是5.30,这个四位小数最大是( ),最小是( )。5.30495.295015、分数的意义和分数单位单位“1”----一个物体,一个计量单位或是许多物体组成的一个整体,都可以用自然数1来表示,通常我们把它叫做单位“1”分 数----分数各部分的名称:分数单位----把单位“1”平均分成若干份,表示其中的一份的数.(表示平均分的份数)(表示所取的份数)把单位“1”平均分成若干份,表示这样的一份或者几份的数,叫做分数.16、分数的分类真分数----
如:
假分数----分子比分母小的分数.分子比分母大或者分子和分母
相等的分数.真分数 < 1假分数 ≥ 15 13
6 29
如: 13 25
9 1817、分数与除法分数与除法的关系:被除数÷除数=(除数≠0)把单位“1”平均分成( )份,取其中的( )份. 把5平均分成9份,取其中的( ),
用字母表示:951份18、分数大小的比较★分母相同的两个分数,分子大的分数比较大.★分子相同的两个分数,分母小的分数比较大.<><>★分子分母不同的两个分数,先通分, 求出原来几个分母的最小公倍数,然后把各个分数分别化成用这个最小公倍数作分母的分数.<19、分数的基本性质 分数的分子和分母同时 乘或者除以相同的数
(零除外),分数的大小不变.一个分数:
如果分母不变,分子乘以3,则这个分数( )
如果分子不变,分母除以3,则这个分数( )扩大3倍扩大3倍如: 3
43×6
4×6==18
2427
48=27÷3
48÷3=9
1620、最简分数*计算结果,能约分的要约分,一般要约成最简分数;假分数的,一般要化成带分数或整数.*判断一个最简分数能不能化成有限小数:分母中除了2和5以外,不含有其他的质因数,就能化成有限小数.√××
√√√*分子分母是互质数的分数——叫最简分数如:21、约分约分------把一个分数化成和它相等,但分子和分母
都比较小的分数.约分的方法:
1.用分子分母的公因数(1除外)依次去除分子和分母,直至得到分子分母是互质数的最简分数为止.
2.或者用分子和分母的最大公因数去除分子和分母.随堂练习
1、5/8表示把单位“1”平均分成( )份,取其中的( )份,它还表示把( )平均分成( ),其中的( )份是多少。
2、把4吨化肥平均分给5户农民,平均每户农民分得这些化肥的( ),每户分得( )吨。
3、把5/12的分母加上36,要使分数的大小不变,分子应加上( )。
4、当a( )时,8/a是真分数,当a( )时,8/a是假分数。
5、5/9千米表示1千米的( ),也可以表示( )千米的1/9。
6、把2米长的绳子平均分成7份,每份长( )米,每份占全长的( )。
7、分母是8的最简真分数的和是( )。
8、比7/8小且比5/8大的分数有( )个。22、百分数的意义表示一个数是另一个数的百分之几的数叫百分数.
百分数又叫百分率或百分比.你能在下面的数轴上给这些车找到停车位吗?0.57/103.56/23/32-2.5
结合实例说一说分数和百分数有什么联系和区别?分数:既可以表示一个数,又可以表示两个数的比。
百分数:只表示两个数的比。百分数的分母固定是100,通常不写成分数形式,写成( )%,不能带单位。百分数的分子可以小于100,也可以大于等于100,可以是整数,也可以是小数。23、分数、小数、百分数的互化小数分 数百分数0.25=( )小数点向右移动两位,添上%0.35%=( )去掉%,小数点向左移动两位先化成小数,再化成百分数先写成分数,再约分先用分数表示,再约分分子除以分母=40%=2
51
6≈0.167=16.7%1
4=1÷4=0.251.2=25%0.0035二、数的整除
1. 整除与除尽
2. 因数和倍数
3. 能被2.3.5整除的数的特征
4. 偶数和奇数
5. 质数和合数
6. 质因数和分解质因数
7. 最大公因数和最小公倍数1. 整除与除尽★整除:整数a除以整数b(b≠0),除得的商是整数而没有余数,我们就说数a能被数b整除,或数b能整除a.★除尽:数a除以数b(b≠0),除得的商是整数或是有限小数,
这就叫做除尽.整除是除尽的一种特殊情况,整除也可以说是除尽,
但除尽不一定是整除.★区别:如:12÷4=3我们就说:12能被4整除;或者说4能整除12.(即:商可以是小数)如:5÷8=0.625(我们不能说5能被8整除,只能说5能被8除尽。)2. 因数和倍数如果数a能被数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数.一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身.一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数.
因数和倍数是相互依存的。不能只说某个数是倍数,某个数是因数。
如:12÷4=312就叫做4的倍数,4就叫做12的因数.
如:12是倍数,
4是因数…都是错的。3. 能被2.3.5整除的数的特征★能被2整除的数的特征:
★能被5整除的数的特征:
★能被3整除的数的特征:
个位上是0,2,4,6,8。个位上是0或5。 各个数位上的数字之和能被3整除。★能同时被2,5整除的数的特征:个位是0。★能同时被2,3,5整除的数的特征:个位是0,而且各个数位上的
数字之和能被3整除.★注意:
有一些数能被7,9,11,13整除,但是不容易看出来,
这是大家在约分中容易忽略的,平时练习中要多注意。4. 偶数和奇数一个自然数,不是奇数就是偶数。偶数:能被2整除的数叫做偶数。奇数:不能被2整除的数叫做奇数。偶数±偶数=( )偶数×偶数=( )偶数偶数偶数偶数奇数奇数★最小的偶数是:★最小的奇数是:01奇数±奇数=( )偶数±奇数=( )
奇数×奇数=( )偶数×奇数=( )
5. 质数和合数质数(素数):只有1和它本身两个因数的数。合数:除了1和它本身还有别的因数的数。1: 既不是质数也不是合数。最小的质数是:最小的合数是:246. 质因数和分解质因数质因数:分解质因数:每一个合数都可以写成几个质数相乘的形式,
这几个质数叫做这个合数的质因数.把一个合数用几个质因数相乘的形式表示出来.
叫做分解质因数. 分解质因数的方法:短除法302153530=2×3×5★ 把30分解质因数不能写成:2×3×5=30也不能写成: 30=1×2 ×3 ×5
因为1不是质数7. 最大公因数(公约数)和最小公倍数
1、公因数(公约数):其中最大的一个叫做这几个数的最大公因(约)数.
例:8和12的公因(约)数有( ),( )是8和12的最大公因数.1、2、443、公倍数:几个数公有的倍数,叫做这几个数的公倍数,
例:4和6的公倍数有( ),( )是4和6的最小公倍数.
12、24、36…125、互质数:公因(约)数只有1的两个数叫做互质数.⑴、两个数都是质数,这两个数一定互质数. 如:9和13
⑵、相邻的两个自然数一定互质数. 如:15和16
⑶、相邻的两个奇数一定互质数. 如:25和27
(4)、1和任何自然数都是互质数. 如:1和20
(5)、两个数都是合数也有可能是互质数。 如:8和156、互质数的几种特殊情况:2、最大公因(约)数:几个数公有的因数,叫做这几个数的公因(约)数;
(公倍数没有最大的)4、最小公倍数:其中最小的一个叫做这几个数的最小公倍数.
8、求最大公因(约)数和最小公倍数如:4和28 最大公因数是( ); 最小公倍数是( )。
★如果较小数是较大数的因数:
较小数就是这两个数的最大公因(约)数;
较大数就是这两个数的最小公倍数.如:4和15 最大公因数是( ); 最小公倍数是( )。★如果两个数是互质数:
它们的最大公因数就是1;
最小公倍数就是它们的乘积.42816024 362121826932324和36的最大公因数是:2×2×3=1224和36的最小公倍数是: 2×2×3×2×3=72除到商是互质数为止除数相乘所有的除数和商相乘如:求24和36的最大公因数和最小公倍数9、用短除法求最大公因数和最小公倍数一般用质数除。随堂练习判断:
1、互质的两个数,没有公因数。( )
2、所有自然数,不是奇数就是偶数。( )
3、36÷9=4,所以36是倍数,9是因数。( )
4、一个数的倍数总比这个数的因数大。( )随堂练习1、7□6□既有因数3,同时又是2和5的倍数,这个四位数是( )。
2、两个质数的积,一定是( )。
3、12的因数有( )。
4、若a=8b,(a、b都不为0),则a、b的最大公因数是( ),最小公倍数是( )。
5、相邻两个质数的和最小是( )。
6、在0~20中,奇数有( ),偶数有( ),质数有( ),合数有( ),2的倍数有( ),3的倍数有( ),5的倍数有( )。随堂练习7、A和B都是自然数,且A÷B=7,那么A与B的最大公因数是( ),最小公倍数是( )。
8、A、B两个数分解质因数分别是A=2×3×7,B=2×5×7。A、B的最大公因数是( ),最小公倍数是( )。
9、8个连续自然数的和是284,这8个自然数分别是( )。
10、9个连续偶数的和是90,这9个连续偶数分别是( )。
11、7个连续自然数的和为35,这7个自然数分别是( )。一、用公因数知识解决生活问题。1、用96朵红玫瑰和72朵白玫瑰做成花束。如果每个花束里的红玫瑰和白玫瑰的朵数相同且没有剩余,最多可以做多少个花束?每个花束里至少要有几朵束? 每个花束里的红玫瑰和白玫瑰的朵数相同,又要求花束的个数最多,所以花束的个数应该是96和72的最大公因数。 (96,72)=24
96÷24+72÷24=7(朵)一、用公因数知识解决生活问题。2、将一张长75厘米,宽60厘米的硬纸板剪成多个同样大小的正方形,使得硬纸板没有剩余,并且剪成的正方形的面积尽可能大,一共可以剪几个相同的正方形? 剪同样大小的正方形且没有剩余,则正方形的边长是长和宽的公因数,为使面积最大,正方形的边长应是长和宽的最大公因数。 (75,60)=15
(75÷15)×(60÷15)=20(个) 变一变:将一张长1.36米,宽0.8米的长方形纸片,裁成一样大小的正方形纸片,并使它们的面积尽可能的大表没有剩余,则一共可裁出多少张? (136,80)=8
(136÷8)×(80÷8)=170(个)二、用公倍数知识解决生活问题。1、暑假期间,小明和小兰都去参加游泳训练,8月1日两人同时参加游泳训练后,小明每6天去一次,小兰每8天去一次,那么几月几日两人再次相遇? 由题意可知,两个人要再次相遇,相隔的天数应分别是6的倍数,也是8的倍数,那么相隔的天数应是6和8的最小公倍数。 [ 6,8 ]=24
所以再次相遇应是8月25日。二、用公倍数知识解决生活问题。2、一筐苹果,如果3个3个地数,最后余2个,如果5个5个地数,最后余4个,如果7个7个地数,最后余6个。这筐苹果最少有多少个? 由题意可知,假设再添上1个苹果,则余下的苹果数分别是3、5、7,就正好再数一次,正好数完,也就是总数加上1后是3、5、7的最小公倍数。 [ 3,5,7 ]=105
105-1=104(个) 变一变:有一盒巧克力,7粒7粒地数还余4粒,5粒5粒地数又少3粒,3粒3粒地数正好数完。这盒巧克力至少有多少粒? 由题意可知,如果巧克力再多3粒,就正好是7、5、3的倍数,所以这盒巧克力至少的粒数就是求7、5、3的最少公倍数再减3。
7×5×3-3=102(粒)练习1、体育课上,老师为同学们整队时发现,无论是3人一排,4人一排,还是5人一排都多2个人,如果老师让全班站成两列纵队,每队几个人?(全班不超过100人)
2、有三根铁丝,一根长18米,一根长24米,一根长30米,现在要把它们截成同样长的小段,每段最长几米?一共可以截多少段?
3、一张长42厘米,宽35厘米的长方形纸,把这张纸剪成正方形小纸片。要使小正方形尽可能的大,可剪多少个小正方形?正方形的边长是多少厘米?
4、一堆糖果,如果平均分给4个小朋友,还剩3个;如果平均分给5个小朋友,还缺1个;如果平均分给6个小朋友,也缺1个,这堆糖果至少有多少个?练习5、一个小数的小数点向左移动两位,所得到的新数比原数小3.564,原数是多少?
6、甲数比乙数少34.65,甲数的小数点向右移动一位正好与乙数相等。甲、乙两数各是多少?
7、小明家的电话号码是由7个数字组成的。以下是电话号码ABCDEFG的密码:A减1就是最小的质数;B既是偶数,又是质数;C是最大的一位数;D是2和3的最小公倍数;E是10以内最大的质数;F既不是正数,也不是负数;G是最小的质数减1。小明家的电话号码是多少?10、倒数的认识乘积是1的两个数互为倒数。如: × = 1 和 互为倒数。就是 的倒数是 , 的倒数是 。★互为倒数的两个数是互相依存的,不能只单独说某个数 是倒数。一定要说“谁”是“谁”的倒数。★求一个数(0除外)的倒数,只要把这个数的分子、分母调换位置。分子、分母调换位置12分子、分母调换位置1 的倒数还是( ) ,1 ( )没有倒数。0
