数学六年级下人教版6.2图形的认识与测量课件(86张)
文档属性
| 名称 | 数学六年级下人教版6.2图形的认识与测量课件(86张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-17 11:05:31 | ||
图片预览







文档简介
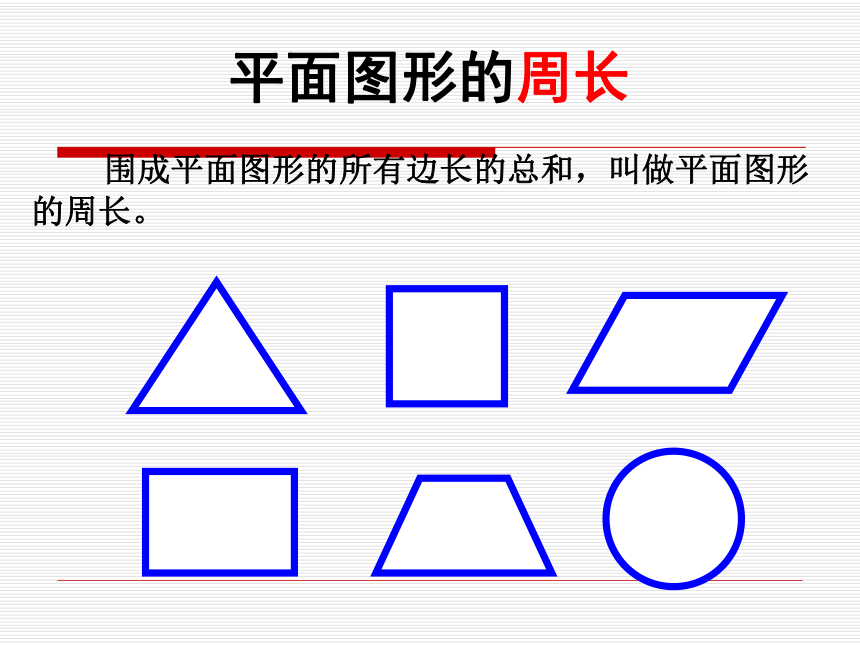
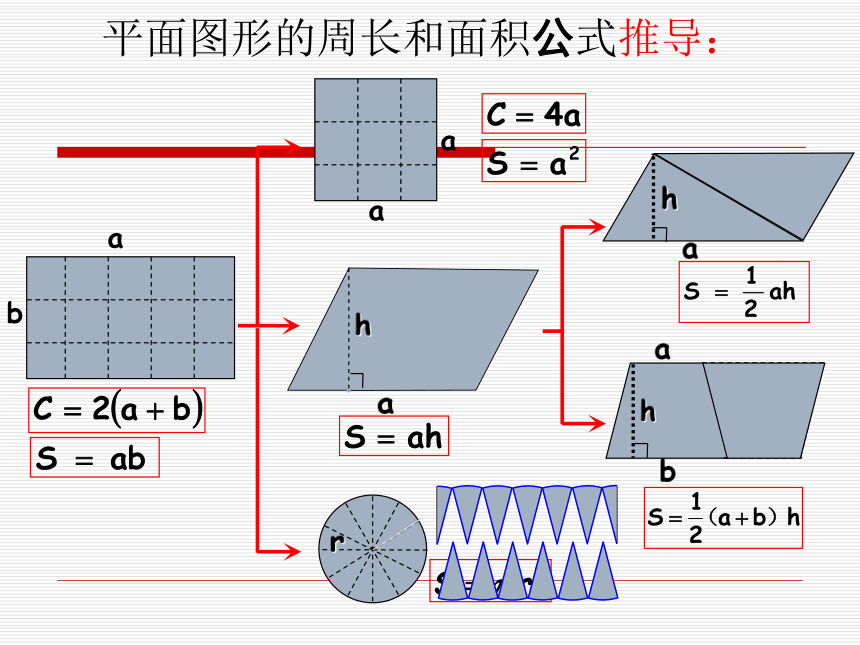
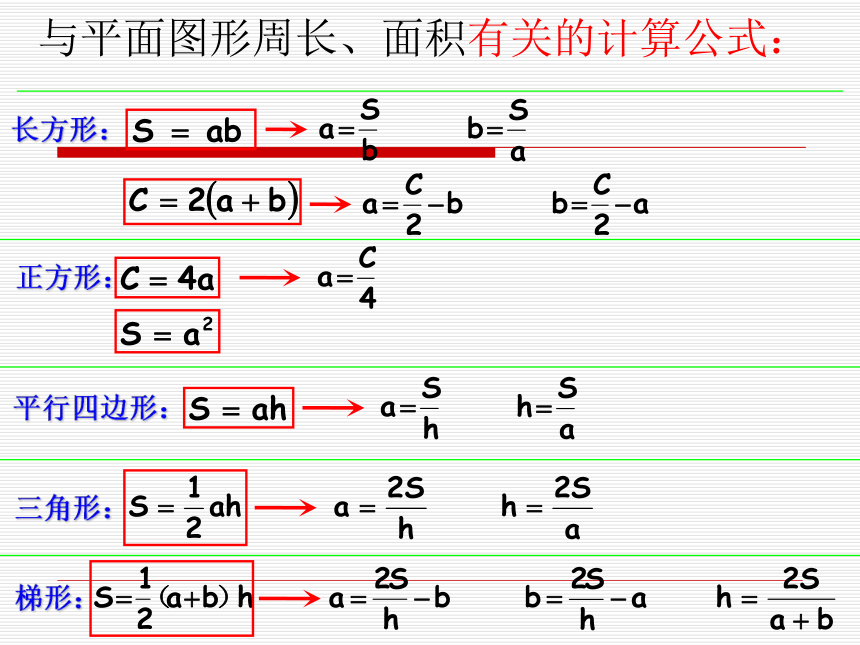
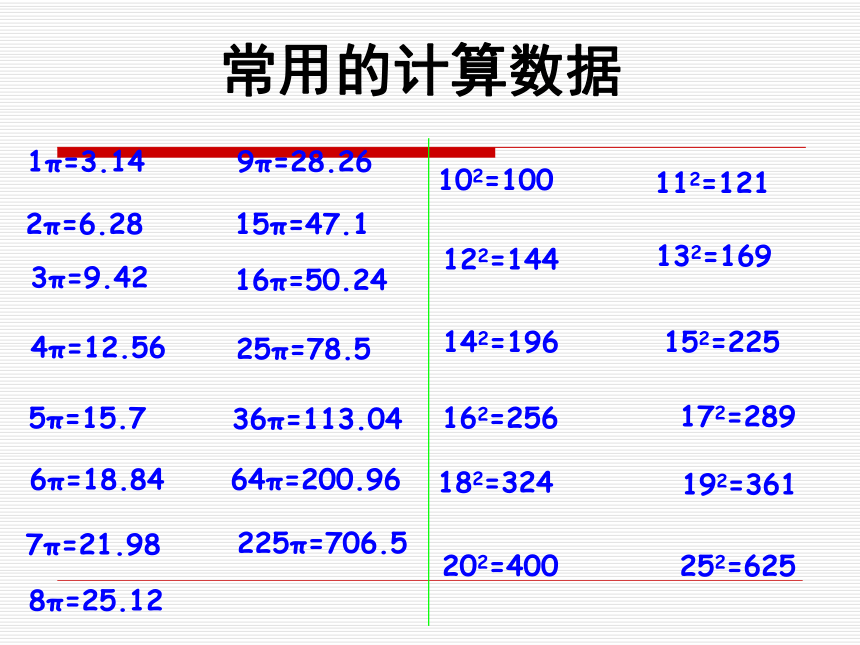
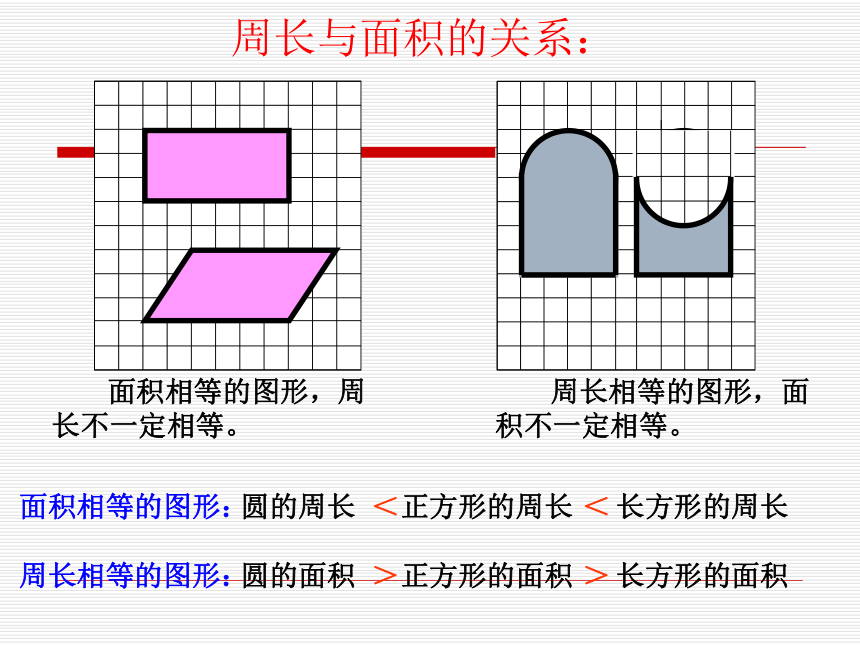
课件86张PPT。小学数学总复习图形的认识与测量(一)平面图形的周长与面积平面图形的周长 围成平面图形的所有边长的总和,叫做平面图形的周长。平面图形的面积: 物体表面的大小或物体所占平面的大小,叫做面积。abaaahahabhr平面图形的周长和面积公式推导:平行四边形:长方形:三角形:梯形:与平面图形周长、面积有关的计算公式:正方形:r=d÷2r=C÷π÷2d=2rd=C÷πC=2πrC=πdS=πr2S=π(d÷2)2S=π(C÷π÷2)2与圆有关的计算公式圆环面积:S环=πR2 -πr2S环=π(R2 -r2)扇形面积:1π=3.14常用的计算数据2π=6.283π=9.424π=12.565π=15.76π=18.847π=21.988π=25.129π=28.2616π=50.2425π=78.536π=113.0464π=200.9615π=47.1102=100112=121122=144132=169142=196152=225225π=706.5162=256172=289182=324192=361202=400252=625 周长相等的图形,面积不一定相等。周长与面积的关系: 面积相等的图形,周长不一定相等。面积相等的图形:圆的周长<正方形的周长长方形的周长<周长相等的图形:圆的面积>正方形的面积>长方形的面积巩固练习1、面积相等的两个梯形一定可以拼成一个平行四
边形。 ( )
2、面积相等的两个三角形形状也相同。( )
3、同底等高的两个三角形的面积一定相等。( )
4、周长相等的长方形和平行四边形,他们的面积一
定相等。( )
5、底和高都是0.2厘米的三角形的面积是0.2平方
厘米。( )判 断××√××6、平行四边形的底越长,它的面积就越大。( )
7、三角形的面积是平行四边形面积的一半。( )
8、两个三角形的高相等,它们的面积就相等。( )
9、大于90°的角叫钝角。( )
10、角的两条边越长,角就越大。( )
11、钟表的分针旋转一周,时针旋转30°。( )
12、可以画一条长10厘米的直线。( )
13、用3根长度分别是8厘米、12厘米、3厘米的小
棒,能围成一个三角形。( )判 断×××√×√××判 断14、平角就是一条直线。( )
15、任意一个三角形的三个内角的和都是180°。( )
16、任意的三条线段都可以围成一个三角形。( )
17、每个三角形至少有2个锐角。( )
18、有一组对边平行的四边形是梯形。( )
19、两端都在圆上的线段是直径。( )××√×√×判 断20、两个半圆一定能拼成一个圆。? ( )
21、半径是2厘米的圆,周长和面积相等( )
22、大圆的圆周率比小圆的圆周率大。 ( )
23、半圆形纸片的周长就是圆周长的一半。( )
24、把半径3厘米的圆等分成十六份,拼成一个近似
长方形,长方形的周长比圆的周长长。 ( )××××√判 断25、在同一个圆内只能画100条直径。( )
26、所有的圆的直径都相等。( )
27、等圆的半径都相等。( )
28、两端都在圆上的线段叫做直径。( )
29、圆心到圆上任意一点的距离都相等。( )
30、半径是2厘米的圆比直径是3厘米的圆大。( )√××√√×1、 圆中心的一点叫做( ),一般用字母( )表示。
2、 连接圆心和圆上任意一点的线段叫做( ),一般用字母r表示。
3、通过圆心并且两端都在圆上的线段叫做( ),一般用字母d 表示。
4、一个圆内有( )条直径,( )条半径。并且( )条直径等于2 条半径。
5、圆是( )图形,有( )条对称轴。
6、把圆规的两脚分开,定好两脚间的距离作为( )。
7、圆是平面上的一种( )图形。圆的两条直径的交点是圆的( )。圆心 O半径直径无数无数 1轴对称半径无数 曲线圆心 填空: 8、把一个圆形纸片沿半径平均分成若干等份,拼成一个近似的长方形。则面积( ),周长( )。
9、周长相等的圆、正方形和长方形,( )的面积最大。
10、圆中最长的线段是圆的( )。
11、把一个直径是10厘米的圆剪成两个半圆,则两个半圆周长的和是( )厘米。不变增加圆直径51.4 填空: 12、用圆规画一个周长12.56厘米的圆,圆规两脚之间的距离是( )厘米,所画圆的面积是( )平方厘米。
13、圆的半径扩大3倍,直径扩大( )倍,周长扩大( )倍;面积扩大( )倍。
14、小铁环直径6分米,大铁环直径8分米。小铁环和大铁环半径的比是( );周长的比是( );面积的比是( )。如果它们滚过相同的路程,则转动的圈数的比是( )。
15、在一张长60厘米,宽40厘米的长方形纸上剪一个最大的圆,则圆的面积是( )平方厘米。212.563393:43:49:163:41256 填空: 填空: 16、三角形的一个内角正好等于其余两个内角的和,这是一个(??? )三角形。
17、一个等腰三角形,它的顶角是72o,它的底角是(??? )度。18、6时整,时针与分针组成的角的度数是( )
19、一个等腰三角形的两条边分别是5厘米和8厘米,那么它的周长最多是(?? )厘米,最少是(??? )厘米。
20、用圆规画一个周长是12 .56厘米的圆,圆规两脚间的距离应该是(???? )厘米。
21、用360厘米长的铁丝围成一个三角形,三条边长度的比是1:2:3,它的三条边的长度分别是(???? )、(???? )和(???? )厘米。正54180o211826012018022、工人叔叔把电线杆上的线架和自行车架子做成三角形,这是应用了三角三具有( )的特性,而推拉或防盗门则是由许多小平边四边形组成的,这是应用平行四边形( )的特性。 填空:
23、一个等边三角形,它的每个内角都是( )度,等腰直角三角形的两个底角都是( )度。24、三角形三个角度数的比是2:4:3,最大的角是( )。不易变形容易变形60458025、一个直角三角形的三条边分别长6厘米、8厘米和10厘米。这个三角形的面积是( )平方厘米。
26、一个正方形周长是1.2米,它的面积是( )平方米。
27、一个等腰三角形的两条边分别是2厘米和5厘米,这个等腰三角形的周长是( )厘米。240.0912 填空: 28、一个平角按4∶5分成两个角。这两个角的度数分别是( ?? )和( ? ?)。
29、一个直角三角形的一个锐角是35度,另一个锐角是( )度。
30、角的两边都是(?? )线。角的大小与(? ?? ?)有关,与( ??)无关。80°100°55射边的长短两边开叉的大小1、画圆时,圆规两脚间的距离是( )。
A.半径长度 B.直径长度
2、从圆心到( )任意一点的线段,叫半径。
A.圆心 B.圆外 C.圆上
3、通过圆心并且两端都在圆上的( )叫直径。
A.直线 B.线段 C.射线ACB 选择: 4、周长相等的长方形、正方形和圆中,( )的面积最小。
A、长方形 B、正方形 C、圆
5、把用木条钉成的长方形拉成平行四边形,比较它们的周长和面积。( )
A周长和面积都变化 B、面积变化,周长不变
C、周长变化,面积不变
6、用一根长16厘米的铁丝围成一个长方形,如果长和宽都是质数,它的面积是( )平方厘米。
A、6 B、10 C、15 D、21ABC 选择: 7、人们常用三角形的(???? )性生产自行车大梁,运用平行四边形的(???? )性制造电动大门。
A.稳定性???? B.易变形?????? C.平衡性
8、平行四边形有(????? )高,梯形有(????? )条高,三角形有(????? )条高。
A.无数条???? B.一条???????? C.三条
9、圆的半径扩大2倍,则它的直径扩大(???? ),面积扩大(????? )。
A.2倍?????? B.4倍????????? C.8倍 选择: ABAABAB10、一个平行四边形和一个三角形等底等高,已知平行四边形的面积是25平方厘米,三角形的面积是( )平方厘米。
A. 12.5 B. 25 C. 50
11、一个长方形的长和宽各增加4厘米,它增加的面积是( )平方厘米。
A.等于16平方厘米 B. 小于16平方厘米
C. 大于16平方厘米
12、已知半圆的直径是8厘米,求它的面积。正确列式( )。
A. 3.14×82÷2
B. 3.14×(8÷2)2÷2
C. 3.14×8÷2+8 选择: ACB解决问题1、把一个圆分割拼成一个近似的长方形,长方形的周长比圆的周长多10厘米,求圆的面积。3.14×(10÷2)2=3.14×52=3.14×25=78.5(cm2)解决问题2、求右面图形的面积。(单位:厘米)15×8÷2 +(15+25)×10÷2 + 25×9﹦60+200+225﹦485S﹦ah÷2+ (a+b)h÷2 + ah答:它的面积是485平方厘米。解决问题3、一块周长为120米的正方形地与一块三角形地的面积相等,三角形地的底为60,求三角形地的高是多少? 【解题思路导引】找出正方形的面积→S正方形=S三角形→三角形的高正方形的边长为:120÷4=30(m)
三角形面积为:30×30=900 (m2)
三角形的高为:900×2÷60=30(m)
答:三角形地的高为30米。解决问题长方形的宽为:
圆的半径为:10÷2=5(m)
圆的面积为:52×3.14=78.5(m2)
答:圆的面积是78.5平方米。小学数学总复习
图形与几何图形的认识与测量(二)立体图形的表面积与体积长方体、正方体、圆柱体、圆锥体的特征:①有6个面,每个面一般是长方形,特殊情况有两个面是正方形,相对的两个面面积相等。
②有12条棱,相对的四条棱互相平行且相等。
③有8个顶点,相交于同一顶点的三条棱分别叫长、宽、高。①有6个面,每个面都是正方形,每个面面积都相等。
②有12条棱,每条棱长度都相等。
③有8 个顶点。①有两个底面,是相等的两个圆。
②有一个侧面,是个曲面,沿高展开一般是个长方形。(当底面周长和高相等时是正方形。)
③有无数条高,每条高长度都相等。①有一个底面,是个圆形。
②有一个侧面,是个曲面,展开是个扇形。
③有一个顶点,
④有一条高。长方体的表面积:上上下前后上下前后左上下前后左右上下前后左右上下前后左右下前后上左右上下前后左右上下前后左右10厘米(长)6厘米(宽)2厘米(高) (0.7×0.5+0.7×0.4+0.5×0.4)×2 0.7×0.5×2+0.7×0.4×2+0.5×0.4×2上和下前和后右和左长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2上(或下)前(或后)右(或左)长方体的表面积=(长×宽+长×高+高×宽)× 2正方体的表面积:上下前后左右正方体的表面积=棱长×棱长×6或=棱长2×66分米6分米6分米62×6底面底面侧面圆柱的表面积 =两个底面的面积+圆柱的侧面积 S表=2S底+S侧圆柱的表面积:圆柱的侧面积怎样计算呢?底面底面底面的周长高侧面圆柱的侧面积 = 底面周长 × 高S侧=Ch长5厘米宽4厘米高3厘米长方体的体积正好等于它的长、宽、高的乘积。长方体的体积=长×宽×高V=abh长方体的体积=底面积×高长方体的体积:棱长4厘米棱长4厘米棱长4厘米 因为正方体是长、宽、高都相等的长方体,所以正方体的体积=棱长×棱长×棱长或正方体的体积=底面积×高正方体的体积:长方体体积=底面积×高圆柱体积==底面积×高长方体的底面积等于圆柱的 底面积 , 高等于圆柱的 高 。 V=Sh圆柱的体积: 圆锥的体积正好等于与它等底等高的圆柱体积的三分之一。因为 V圆柱=ShS=πr2圆锥的体积长方体、正方体、圆柱体、圆锥体的相关计算:4a+4b+4h
或4(a+b+c)S长=2ab+2ah+2bh
=(ab+ah+bh)×2S正=a2×6S表=2S底+S侧
S侧=ChV长=abh12aV正=a3 V柱=ShV=Sh 长方体的长、宽、高都变为原来的2倍,它的表面积和体积发生了什么变化?2268848352384我发现了:长方体的长、宽、高都变为原来的n倍,它的表面积跟着变为原来的n2倍,体积也跟着变为原来的n3倍,棱长和变为原来的n倍。盒子的体积与盒子的容积哪个大 ?仔细观察: 对于同一个容器,它的体积一定比容积大,因为它有厚度。物体的容积: 容器的容积计算方法同体积的计算方法一样,但是要从容器的里面量数据。表面积、体积、容积的对比:物体表面面积的总和(所有面面积的总和)物体所占空间的大小容器所能容纳物体体积的大小m2 dm2 cm2m3 dm3 cm3m3 dm3 cm3
L ml1m2=100dm2
1dm2=100cm21m3=1000dm3
1dm3=1000cm31L=1000ml
1dm3=1L
1cm3=1ml练习√× 判断: × × × 6、计算圆柱形油桶能装多少升油就是求这个油桶
的容积。( )
7、圆柱底面直径扩大2倍,高不变,它的体积也扩
大2倍。( )
8、圆柱的底面周长和高相等时,它的侧面展开图一
定是正方形。( )
9、求做一个圆柱形的通风管需要多少铁皮,就是求
圆柱的表面积。( )√× √× 判断: 14、两个大小相等的正方体合在一起,成了一个长方体,那么它就有12个面。( )12、如果一个长方体的12条棱都相等,这个长方体
就是正方体。?? ( )10、正方体6个面的形状相同、大小相等。( ) 11、有6个面,12条棱、8个顶点的形体一定是长方体。
( )13、一个长方体的所有面都是长方形的。( )√×× ×√ 判断: 15、长方体和正方体都有6个面,12条棱,8个顶点。 ( )
16、正方体的六个面面积一定相等。( ) 17、一个长方体(非正方体)最多有四个面面积相等。( )
18、一个木箱的体积就是它的容积。( ) 19、长方体是特殊的正方体。( ) 20、棱长6分米的正方体,它的表面积和体积相等。 ( ) 21、用4个棱长1厘米的小正方体可以拼成一个大正方体。( )√√√×××× 判断: 22、相交于一个顶点的三条棱相等的长方体一定是正方体。( )
23、 长方体有6个面,每个面有4条棱,共24条棱。( ) 24、长方体是一种特殊的正方体。( ) 25、相对的4条棱都相等的物体一定是长方体。( )
26、圆柱的侧面展开一定是长方形。( )
27、 这面小旗旋转一周产生的图形是圆锥体。( )
28、一根长24厘米的铁丝制作成一个正方体框架,棱长是3厘米。( )√××× 判断: ×√×29、体积单位间的进率都是1000 。 ( )
30、把一个正方体的橡皮泥捏成一个长方体后虽然它的形状变了,但是它所占的空间大小不变。( )
31、正方体的棱长扩大2倍,它的体积就扩大6倍。( )
32、冰箱的容积就是冰箱的体积( )
33、一个薄塑料长方体(厚度不计),它的体积就是容积。( )
34、一个油桶能装多少升油,就是求它的容积。( )×√× 判断: ×√√ 1、把一个圆柱的底面平均分成若干个扇形,然后切开拼成一个近似的长方体。下面哪句话是正确的?( )
A、表面积和体积都没变化。
B、表面积和体积都发生了变化。
C、表面积变了,体积没变。
D、表面积没变,体积变了。
C 选择: A、54 B、18 C 、0.6 D、6 2、等底等体积的圆柱和圆锥,圆锥的高是18厘米,那么圆柱的高是( )厘米。D 选择: 3、等高等体积的圆柱和圆锥,圆柱的底面积是6平方厘米,那么圆锥的底面积是( )平方厘米。A、6 B、18
C、2 D、36
B 选择: 4、把一个底面半径是2分米、高是3分米的圆柱形容器中注满水,现垂直轻轻插入一根底面积是5平方分米,高是4分米的方钢,溢出水的体积是( )毫升。
A、20 B、15 C、20000 D、15000D 选择: 回答下面的问题,并列出算式(不计算):
1、一个圆柱形无盖的水桶,底面半径10分米,高20分米。
(1)给这个水桶加个箍,是求什么?
(2)求这个水桶的占地面积,是求什么?
(3)做这样一个水桶用多少铁皮,是求什么?
(4)这个水桶能装多少水,是求什么?
2×3.14×103.14×1023.14×102+2×3.14×10×203.14×102×20 基本练习: 2、做一个圆柱形的油箱,底面半径3分米,高4分米。至少需要铁皮多少平方分米?
3、做一个圆柱形的水桶,底面直径6分米,高4分米。至少需要铁皮多少平方分米?
4、做一节圆柱形的通风管,底面周长18.84分米,长4分米。至少需要铁皮多少平方分米?18.84 × 43.14 ×32×2 + 2×3.14×3×4 基本练习: 5、一个鱼塘长8m,宽4.5m,深2m,这个鱼塘的容积是多少立方米? 8×4.5×2
=36×2
=72(m2)
答:这个鱼塘的容积是72m2。 基本练习: 6、新建的篮球馆要铺设3cm厚的木质地板,已知该馆的长36m,宽20m,铺设它至少需要用多少方木材? 3mm=0.003m
36×20×0.003
=720×0.003
=2.16(m3)
答:铺设它至少需要用2.16m3木材。 基本练习: 7、把两个棱长是4厘米的正方体木块粘合成一个长方体,这个长方体的表面积是多少平方厘米?方法三、4×4×10=160(平方厘米)方法一、(8×4+8×4+4×4)×2=160(平方厘米)方法四、4×4×12- 4×4×2=160(平方厘米)方法二、8×4×4 + 4×4×2=160(平方厘米) 基本练习: 8、用铁丝做一个长10厘米,宽5厘米,高4厘米的长方体框架,至少需要多长的铁丝?在这个长方体框架外面糊一层纸,至少需要多少平方厘米的纸?1054(1)求至少需要多长的铁丝?
(10+5+4)×4=76 (厘米)(2)求至少需要多少立方厘米的纸?
(10×5+10×4+5×4)×2=220(平方厘米) 基本练习: 拓展练习: 1、圆柱长10厘米,接上4厘米的一段后,表面积增加了25.12平方厘米,求原来圆柱的体积是多少立方厘米?25.12÷4÷3.14÷2(1)求底面半径:=6.28÷3.14÷2=1(cm)(1)求原来的圆柱体积:3.14×12×10=31.4(cm2)答:原来圆柱的体积是31.4cm3。2、把一根长30厘米的长方体木料锯成3段(如图),表面积比原来增加了20平方厘米,这根木料原来的体积是多少立方厘米?20÷4=5(平方厘米)30×5=150(平方厘米)答:这根木材原来的体积是150平方厘米。 拓展练习: 3、一个底面是正方形的长方体,把它的侧面展开后得到一个边长是12厘米的正方形。求这个长方体的体积是多少?1212123312÷4=3(厘米)3×3×12=108(立方厘米)答:这个长方体的体积是108立方厘米。 拓展练习: 4、一个圆柱形木材,沿着一条底面直径纵向剖开,量得一个纵剖面面积是6平方分米,那么,圆柱的侧面积是多少平方分米?3.14×6=18.84(平方分米) 拓展练习: 2、将一个圆柱体沿着底面直径切成两个半圆柱,表面积增加了40平方厘米,圆柱的底面直径为4厘米,这个圆柱的体积是多少立方厘米? 拓展练习: (1)正方体体积: 103=1000(cm3)(2)圆锥的底面积:3.14×(10÷2)2=78.5(cm2)(3)圆锥的高:1000×3÷78.5≈38(cm)(1)表面积:
202×5+3.14×102+2×3.14×10×20÷2
=2000+314+628
=2942(cm2)(2)体积:
203+3.14×102×20÷2
=8000+3140
=11140(cm3)(1)10个正方形。(2)体积:53×10=1250(cm3)(3)表面积:52×34=850(cm2)
边形。 ( )
2、面积相等的两个三角形形状也相同。( )
3、同底等高的两个三角形的面积一定相等。( )
4、周长相等的长方形和平行四边形,他们的面积一
定相等。( )
5、底和高都是0.2厘米的三角形的面积是0.2平方
厘米。( )判 断××√××6、平行四边形的底越长,它的面积就越大。( )
7、三角形的面积是平行四边形面积的一半。( )
8、两个三角形的高相等,它们的面积就相等。( )
9、大于90°的角叫钝角。( )
10、角的两条边越长,角就越大。( )
11、钟表的分针旋转一周,时针旋转30°。( )
12、可以画一条长10厘米的直线。( )
13、用3根长度分别是8厘米、12厘米、3厘米的小
棒,能围成一个三角形。( )判 断×××√×√××判 断14、平角就是一条直线。( )
15、任意一个三角形的三个内角的和都是180°。( )
16、任意的三条线段都可以围成一个三角形。( )
17、每个三角形至少有2个锐角。( )
18、有一组对边平行的四边形是梯形。( )
19、两端都在圆上的线段是直径。( )××√×√×判 断20、两个半圆一定能拼成一个圆。? ( )
21、半径是2厘米的圆,周长和面积相等( )
22、大圆的圆周率比小圆的圆周率大。 ( )
23、半圆形纸片的周长就是圆周长的一半。( )
24、把半径3厘米的圆等分成十六份,拼成一个近似
长方形,长方形的周长比圆的周长长。 ( )××××√判 断25、在同一个圆内只能画100条直径。( )
26、所有的圆的直径都相等。( )
27、等圆的半径都相等。( )
28、两端都在圆上的线段叫做直径。( )
29、圆心到圆上任意一点的距离都相等。( )
30、半径是2厘米的圆比直径是3厘米的圆大。( )√××√√×1、 圆中心的一点叫做( ),一般用字母( )表示。
2、 连接圆心和圆上任意一点的线段叫做( ),一般用字母r表示。
3、通过圆心并且两端都在圆上的线段叫做( ),一般用字母d 表示。
4、一个圆内有( )条直径,( )条半径。并且( )条直径等于2 条半径。
5、圆是( )图形,有( )条对称轴。
6、把圆规的两脚分开,定好两脚间的距离作为( )。
7、圆是平面上的一种( )图形。圆的两条直径的交点是圆的( )。圆心 O半径直径无数无数 1轴对称半径无数 曲线圆心 填空: 8、把一个圆形纸片沿半径平均分成若干等份,拼成一个近似的长方形。则面积( ),周长( )。
9、周长相等的圆、正方形和长方形,( )的面积最大。
10、圆中最长的线段是圆的( )。
11、把一个直径是10厘米的圆剪成两个半圆,则两个半圆周长的和是( )厘米。不变增加圆直径51.4 填空: 12、用圆规画一个周长12.56厘米的圆,圆规两脚之间的距离是( )厘米,所画圆的面积是( )平方厘米。
13、圆的半径扩大3倍,直径扩大( )倍,周长扩大( )倍;面积扩大( )倍。
14、小铁环直径6分米,大铁环直径8分米。小铁环和大铁环半径的比是( );周长的比是( );面积的比是( )。如果它们滚过相同的路程,则转动的圈数的比是( )。
15、在一张长60厘米,宽40厘米的长方形纸上剪一个最大的圆,则圆的面积是( )平方厘米。212.563393:43:49:163:41256 填空: 填空: 16、三角形的一个内角正好等于其余两个内角的和,这是一个(??? )三角形。
17、一个等腰三角形,它的顶角是72o,它的底角是(??? )度。18、6时整,时针与分针组成的角的度数是( )
19、一个等腰三角形的两条边分别是5厘米和8厘米,那么它的周长最多是(?? )厘米,最少是(??? )厘米。
20、用圆规画一个周长是12 .56厘米的圆,圆规两脚间的距离应该是(???? )厘米。
21、用360厘米长的铁丝围成一个三角形,三条边长度的比是1:2:3,它的三条边的长度分别是(???? )、(???? )和(???? )厘米。正54180o211826012018022、工人叔叔把电线杆上的线架和自行车架子做成三角形,这是应用了三角三具有( )的特性,而推拉或防盗门则是由许多小平边四边形组成的,这是应用平行四边形( )的特性。 填空:
23、一个等边三角形,它的每个内角都是( )度,等腰直角三角形的两个底角都是( )度。24、三角形三个角度数的比是2:4:3,最大的角是( )。不易变形容易变形60458025、一个直角三角形的三条边分别长6厘米、8厘米和10厘米。这个三角形的面积是( )平方厘米。
26、一个正方形周长是1.2米,它的面积是( )平方米。
27、一个等腰三角形的两条边分别是2厘米和5厘米,这个等腰三角形的周长是( )厘米。240.0912 填空: 28、一个平角按4∶5分成两个角。这两个角的度数分别是( ?? )和( ? ?)。
29、一个直角三角形的一个锐角是35度,另一个锐角是( )度。
30、角的两边都是(?? )线。角的大小与(? ?? ?)有关,与( ??)无关。80°100°55射边的长短两边开叉的大小1、画圆时,圆规两脚间的距离是( )。
A.半径长度 B.直径长度
2、从圆心到( )任意一点的线段,叫半径。
A.圆心 B.圆外 C.圆上
3、通过圆心并且两端都在圆上的( )叫直径。
A.直线 B.线段 C.射线ACB 选择: 4、周长相等的长方形、正方形和圆中,( )的面积最小。
A、长方形 B、正方形 C、圆
5、把用木条钉成的长方形拉成平行四边形,比较它们的周长和面积。( )
A周长和面积都变化 B、面积变化,周长不变
C、周长变化,面积不变
6、用一根长16厘米的铁丝围成一个长方形,如果长和宽都是质数,它的面积是( )平方厘米。
A、6 B、10 C、15 D、21ABC 选择: 7、人们常用三角形的(???? )性生产自行车大梁,运用平行四边形的(???? )性制造电动大门。
A.稳定性???? B.易变形?????? C.平衡性
8、平行四边形有(????? )高,梯形有(????? )条高,三角形有(????? )条高。
A.无数条???? B.一条???????? C.三条
9、圆的半径扩大2倍,则它的直径扩大(???? ),面积扩大(????? )。
A.2倍?????? B.4倍????????? C.8倍 选择: ABAABAB10、一个平行四边形和一个三角形等底等高,已知平行四边形的面积是25平方厘米,三角形的面积是( )平方厘米。
A. 12.5 B. 25 C. 50
11、一个长方形的长和宽各增加4厘米,它增加的面积是( )平方厘米。
A.等于16平方厘米 B. 小于16平方厘米
C. 大于16平方厘米
12、已知半圆的直径是8厘米,求它的面积。正确列式( )。
A. 3.14×82÷2
B. 3.14×(8÷2)2÷2
C. 3.14×8÷2+8 选择: ACB解决问题1、把一个圆分割拼成一个近似的长方形,长方形的周长比圆的周长多10厘米,求圆的面积。3.14×(10÷2)2=3.14×52=3.14×25=78.5(cm2)解决问题2、求右面图形的面积。(单位:厘米)15×8÷2 +(15+25)×10÷2 + 25×9﹦60+200+225﹦485S﹦ah÷2+ (a+b)h÷2 + ah答:它的面积是485平方厘米。解决问题3、一块周长为120米的正方形地与一块三角形地的面积相等,三角形地的底为60,求三角形地的高是多少? 【解题思路导引】找出正方形的面积→S正方形=S三角形→三角形的高正方形的边长为:120÷4=30(m)
三角形面积为:30×30=900 (m2)
三角形的高为:900×2÷60=30(m)
答:三角形地的高为30米。解决问题长方形的宽为:
圆的半径为:10÷2=5(m)
圆的面积为:52×3.14=78.5(m2)
答:圆的面积是78.5平方米。小学数学总复习
图形与几何图形的认识与测量(二)立体图形的表面积与体积长方体、正方体、圆柱体、圆锥体的特征:①有6个面,每个面一般是长方形,特殊情况有两个面是正方形,相对的两个面面积相等。
②有12条棱,相对的四条棱互相平行且相等。
③有8个顶点,相交于同一顶点的三条棱分别叫长、宽、高。①有6个面,每个面都是正方形,每个面面积都相等。
②有12条棱,每条棱长度都相等。
③有8 个顶点。①有两个底面,是相等的两个圆。
②有一个侧面,是个曲面,沿高展开一般是个长方形。(当底面周长和高相等时是正方形。)
③有无数条高,每条高长度都相等。①有一个底面,是个圆形。
②有一个侧面,是个曲面,展开是个扇形。
③有一个顶点,
④有一条高。长方体的表面积:上上下前后上下前后左上下前后左右上下前后左右上下前后左右下前后上左右上下前后左右上下前后左右10厘米(长)6厘米(宽)2厘米(高) (0.7×0.5+0.7×0.4+0.5×0.4)×2 0.7×0.5×2+0.7×0.4×2+0.5×0.4×2上和下前和后右和左长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2上(或下)前(或后)右(或左)长方体的表面积=(长×宽+长×高+高×宽)× 2正方体的表面积:上下前后左右正方体的表面积=棱长×棱长×6或=棱长2×66分米6分米6分米62×6底面底面侧面圆柱的表面积 =两个底面的面积+圆柱的侧面积 S表=2S底+S侧圆柱的表面积:圆柱的侧面积怎样计算呢?底面底面底面的周长高侧面圆柱的侧面积 = 底面周长 × 高S侧=Ch长5厘米宽4厘米高3厘米长方体的体积正好等于它的长、宽、高的乘积。长方体的体积=长×宽×高V=abh长方体的体积=底面积×高长方体的体积:棱长4厘米棱长4厘米棱长4厘米 因为正方体是长、宽、高都相等的长方体,所以正方体的体积=棱长×棱长×棱长或正方体的体积=底面积×高正方体的体积:长方体体积=底面积×高圆柱体积==底面积×高长方体的底面积等于圆柱的 底面积 , 高等于圆柱的 高 。 V=Sh圆柱的体积: 圆锥的体积正好等于与它等底等高的圆柱体积的三分之一。因为 V圆柱=ShS=πr2圆锥的体积长方体、正方体、圆柱体、圆锥体的相关计算:4a+4b+4h
或4(a+b+c)S长=2ab+2ah+2bh
=(ab+ah+bh)×2S正=a2×6S表=2S底+S侧
S侧=ChV长=abh12aV正=a3 V柱=ShV=Sh 长方体的长、宽、高都变为原来的2倍,它的表面积和体积发生了什么变化?2268848352384我发现了:长方体的长、宽、高都变为原来的n倍,它的表面积跟着变为原来的n2倍,体积也跟着变为原来的n3倍,棱长和变为原来的n倍。盒子的体积与盒子的容积哪个大 ?仔细观察: 对于同一个容器,它的体积一定比容积大,因为它有厚度。物体的容积: 容器的容积计算方法同体积的计算方法一样,但是要从容器的里面量数据。表面积、体积、容积的对比:物体表面面积的总和(所有面面积的总和)物体所占空间的大小容器所能容纳物体体积的大小m2 dm2 cm2m3 dm3 cm3m3 dm3 cm3
L ml1m2=100dm2
1dm2=100cm21m3=1000dm3
1dm3=1000cm31L=1000ml
1dm3=1L
1cm3=1ml练习√× 判断: × × × 6、计算圆柱形油桶能装多少升油就是求这个油桶
的容积。( )
7、圆柱底面直径扩大2倍,高不变,它的体积也扩
大2倍。( )
8、圆柱的底面周长和高相等时,它的侧面展开图一
定是正方形。( )
9、求做一个圆柱形的通风管需要多少铁皮,就是求
圆柱的表面积。( )√× √× 判断: 14、两个大小相等的正方体合在一起,成了一个长方体,那么它就有12个面。( )12、如果一个长方体的12条棱都相等,这个长方体
就是正方体。?? ( )10、正方体6个面的形状相同、大小相等。( ) 11、有6个面,12条棱、8个顶点的形体一定是长方体。
( )13、一个长方体的所有面都是长方形的。( )√×× ×√ 判断: 15、长方体和正方体都有6个面,12条棱,8个顶点。 ( )
16、正方体的六个面面积一定相等。( ) 17、一个长方体(非正方体)最多有四个面面积相等。( )
18、一个木箱的体积就是它的容积。( ) 19、长方体是特殊的正方体。( ) 20、棱长6分米的正方体,它的表面积和体积相等。 ( ) 21、用4个棱长1厘米的小正方体可以拼成一个大正方体。( )√√√×××× 判断: 22、相交于一个顶点的三条棱相等的长方体一定是正方体。( )
23、 长方体有6个面,每个面有4条棱,共24条棱。( ) 24、长方体是一种特殊的正方体。( ) 25、相对的4条棱都相等的物体一定是长方体。( )
26、圆柱的侧面展开一定是长方形。( )
27、 这面小旗旋转一周产生的图形是圆锥体。( )
28、一根长24厘米的铁丝制作成一个正方体框架,棱长是3厘米。( )√××× 判断: ×√×29、体积单位间的进率都是1000 。 ( )
30、把一个正方体的橡皮泥捏成一个长方体后虽然它的形状变了,但是它所占的空间大小不变。( )
31、正方体的棱长扩大2倍,它的体积就扩大6倍。( )
32、冰箱的容积就是冰箱的体积( )
33、一个薄塑料长方体(厚度不计),它的体积就是容积。( )
34、一个油桶能装多少升油,就是求它的容积。( )×√× 判断: ×√√ 1、把一个圆柱的底面平均分成若干个扇形,然后切开拼成一个近似的长方体。下面哪句话是正确的?( )
A、表面积和体积都没变化。
B、表面积和体积都发生了变化。
C、表面积变了,体积没变。
D、表面积没变,体积变了。
C 选择: A、54 B、18 C 、0.6 D、6 2、等底等体积的圆柱和圆锥,圆锥的高是18厘米,那么圆柱的高是( )厘米。D 选择: 3、等高等体积的圆柱和圆锥,圆柱的底面积是6平方厘米,那么圆锥的底面积是( )平方厘米。A、6 B、18
C、2 D、36
B 选择: 4、把一个底面半径是2分米、高是3分米的圆柱形容器中注满水,现垂直轻轻插入一根底面积是5平方分米,高是4分米的方钢,溢出水的体积是( )毫升。
A、20 B、15 C、20000 D、15000D 选择: 回答下面的问题,并列出算式(不计算):
1、一个圆柱形无盖的水桶,底面半径10分米,高20分米。
(1)给这个水桶加个箍,是求什么?
(2)求这个水桶的占地面积,是求什么?
(3)做这样一个水桶用多少铁皮,是求什么?
(4)这个水桶能装多少水,是求什么?
2×3.14×103.14×1023.14×102+2×3.14×10×203.14×102×20 基本练习: 2、做一个圆柱形的油箱,底面半径3分米,高4分米。至少需要铁皮多少平方分米?
3、做一个圆柱形的水桶,底面直径6分米,高4分米。至少需要铁皮多少平方分米?
4、做一节圆柱形的通风管,底面周长18.84分米,长4分米。至少需要铁皮多少平方分米?18.84 × 43.14 ×32×2 + 2×3.14×3×4 基本练习: 5、一个鱼塘长8m,宽4.5m,深2m,这个鱼塘的容积是多少立方米? 8×4.5×2
=36×2
=72(m2)
答:这个鱼塘的容积是72m2。 基本练习: 6、新建的篮球馆要铺设3cm厚的木质地板,已知该馆的长36m,宽20m,铺设它至少需要用多少方木材? 3mm=0.003m
36×20×0.003
=720×0.003
=2.16(m3)
答:铺设它至少需要用2.16m3木材。 基本练习: 7、把两个棱长是4厘米的正方体木块粘合成一个长方体,这个长方体的表面积是多少平方厘米?方法三、4×4×10=160(平方厘米)方法一、(8×4+8×4+4×4)×2=160(平方厘米)方法四、4×4×12- 4×4×2=160(平方厘米)方法二、8×4×4 + 4×4×2=160(平方厘米) 基本练习: 8、用铁丝做一个长10厘米,宽5厘米,高4厘米的长方体框架,至少需要多长的铁丝?在这个长方体框架外面糊一层纸,至少需要多少平方厘米的纸?1054(1)求至少需要多长的铁丝?
(10+5+4)×4=76 (厘米)(2)求至少需要多少立方厘米的纸?
(10×5+10×4+5×4)×2=220(平方厘米) 基本练习: 拓展练习: 1、圆柱长10厘米,接上4厘米的一段后,表面积增加了25.12平方厘米,求原来圆柱的体积是多少立方厘米?25.12÷4÷3.14÷2(1)求底面半径:=6.28÷3.14÷2=1(cm)(1)求原来的圆柱体积:3.14×12×10=31.4(cm2)答:原来圆柱的体积是31.4cm3。2、把一根长30厘米的长方体木料锯成3段(如图),表面积比原来增加了20平方厘米,这根木料原来的体积是多少立方厘米?20÷4=5(平方厘米)30×5=150(平方厘米)答:这根木材原来的体积是150平方厘米。 拓展练习: 3、一个底面是正方形的长方体,把它的侧面展开后得到一个边长是12厘米的正方形。求这个长方体的体积是多少?1212123312÷4=3(厘米)3×3×12=108(立方厘米)答:这个长方体的体积是108立方厘米。 拓展练习: 4、一个圆柱形木材,沿着一条底面直径纵向剖开,量得一个纵剖面面积是6平方分米,那么,圆柱的侧面积是多少平方分米?3.14×6=18.84(平方分米) 拓展练习: 2、将一个圆柱体沿着底面直径切成两个半圆柱,表面积增加了40平方厘米,圆柱的底面直径为4厘米,这个圆柱的体积是多少立方厘米? 拓展练习: (1)正方体体积: 103=1000(cm3)(2)圆锥的底面积:3.14×(10÷2)2=78.5(cm2)(3)圆锥的高:1000×3÷78.5≈38(cm)(1)表面积:
202×5+3.14×102+2×3.14×10×20÷2
=2000+314+628
=2942(cm2)(2)体积:
203+3.14×102×20÷2
=8000+3140
=11140(cm3)(1)10个正方形。(2)体积:53×10=1250(cm3)(3)表面积:52×34=850(cm2)
