2.3平行线的条件与特征综合应用学案
文档属性
| 名称 | 2.3平行线的条件与特征综合应用学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 196.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-17 00:00:00 | ||
图片预览


文档简介
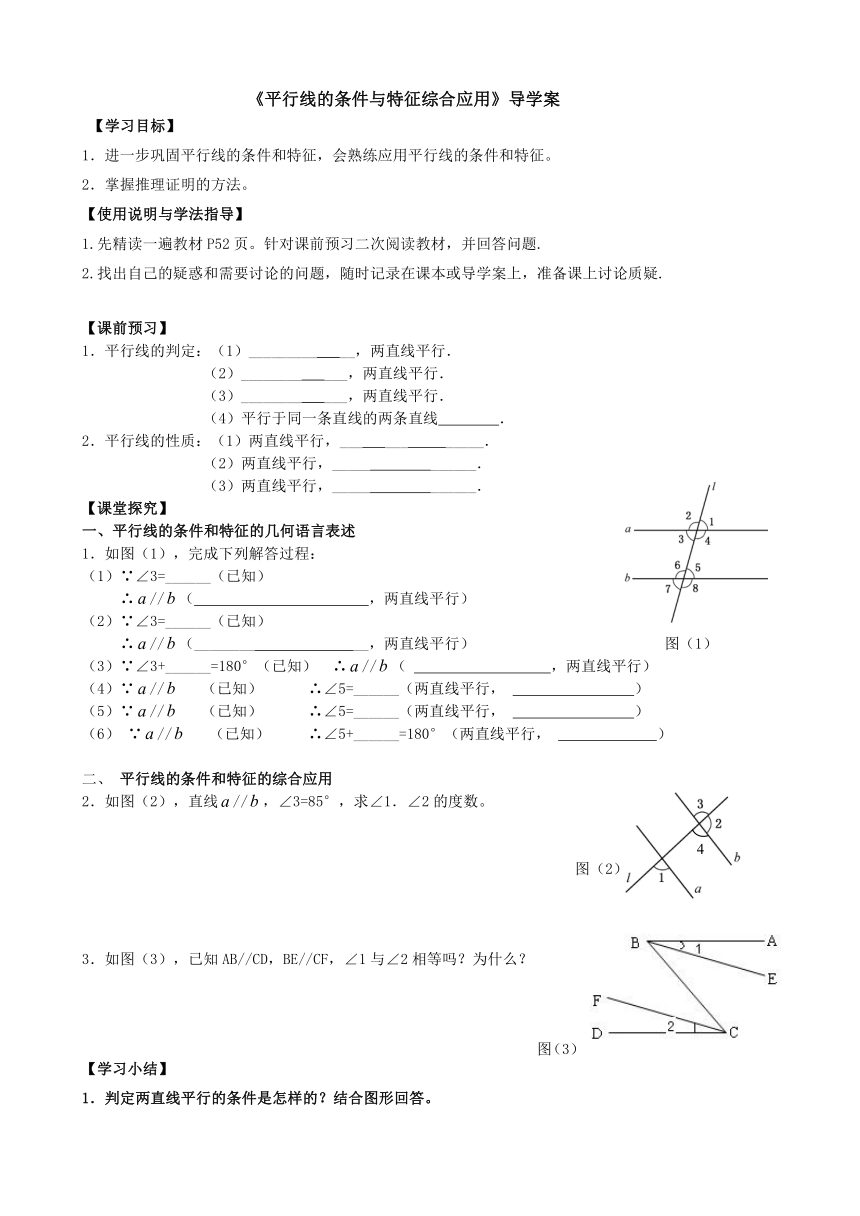
《平行线的条件与特征综合应用》导学案
【学习目标】
1.进一步巩固平行线的条件和特征,会熟练应用平行线的条件和特征。
2.掌握推理证明的方法。
【使用说明与学法指导】
1.先精读一遍教材P52页。针对课前预习二次阅读教材,并回答问题.
2.找出自己的疑惑和需要讨论的问题,随时记录在课本或导学案上,准备课上讨论质疑.
【课前预习】
1.平行线的判定:(1)_________
__,两直线平行.
(2)________
___,两直线平行.
(3)________
___,两直线平行.
(4)平行于同一条直线的两条直线
.
2.平行线的性质:(1)两直线平行,___
___
_____.
(2)两直线平行,_____
______.
(3)两直线平行,_____
______.
【课堂探究】
一、平行线的条件和特征的几何语言表述
1.如图(1),完成下列解答过程:
(1)∵∠3=______(已知)
∴//(
,两直线平行)
(2)∵∠3=______(已知)
∴//(________
__,两直线平行)
图(1)
(3)∵∠3+______=180°(已知)
∴//(
,两直线平行)
(4)∵//
(已知)
∴∠5=______(两直线平行,
)
(5)∵//
(已知)
∴∠5=______(两直线平行,
)
(6)
∵//
(已知)
∴∠5+______=180°(两直线平行,
)
二、
平行线的条件和特征的综合应用
2.如图(2),直线//,∠3=85°,求∠1.∠2的度数。
图(2)
3.如图(3),已知AB//CD,BE//CF,∠1与∠2相等吗?为什么?
图(3)
【学习小结】
1.判定两直线平行的条件是怎样的?结合图形回答。
2.平行线的性质是怎样的?结合图形回答。
【课堂检测】
1.如图(5),下列推理错误的是(
)
A.∵∠1=∠2,
∴∥b
B.∵∠1=∠3,
∴∥b
C.∵∠3=∠5,
∴c∥d
D.∵∠2+∠4=180°,∴c∥d
2.如图(6),在下列四组条件中,能判定AB∥CD的是(
)
A.∠1=∠2
B.∠3=∠4
C.∠BAD+∠ABC=180°
D.∠ABD=∠BDC
3.如图(7),AB∥CD,AF分别交AB.CD于A.C,CE平分∠DCF,∠1=100°,
则∠2=
4.如图(8),AB⊥EF,CD⊥EF,∠1=∠F=45°,那么与∠FCD
相等的角有_______个,它们分别是___________________________。
图(6)
图(7)
图(8)
4.如图,∠CAB=100°,∠ABF=130°,AC∥MD,BF∥ME,求∠DME
的度数。
5.如图,已知∠1=∠2,∠3=115°。求∠4的度数。
6.如图(10),已知A.B.C三点在同一直线上,∠1=∠2,∠3=∠D。试说明:BD//CE。
【巩固作业】
1.如图(1),∥,∠1=120°,∠2=100°,则∠3=
(
)
A.20°
B.40°
C.50°
D.60°
2.如图(2),下列推理中正确的是(
)
A.
∴
B.
∴
C.
∴
D.
∴
3.下列说法正确的是(
)
A.相等的角是对顶角
B.一对同旁内角的平分线互相垂直
C.对顶角的平分线在一条直线上
D.同位角相等
图(1)
图(2)
图(3)
4.若
,则它的余角是_________,它的补角是________.
5.若∠α与∠β是对顶角,且∠α+∠β=1200
,则∠α=
,∠β=
.
6.如图(3),,若,则=
.
7.已知,如图,EF∥BC,∠A=∠D,∠AOB=70°,∠1+∠C=150°,求∠B的度数.
8、如图,已知AB∥CD,∠α=450,∠D=∠C.你能求出∠D、∠C和∠B的度数吗?
9.已知:某品牌不锈钢锥体的平面图如图所示,设计要求是AB∥CD,且∠A=∠C=143°,请你帮设计师计算一下∠E的度数,并说明理由.
10.
如图,∠1=∠2,∠C=∠D,那么∠A=∠F,为什么?
11.
如图,已知:AB∥CD,AE平分∠BAC,CE平分∠ACD,请说明:AE⊥CF.
4
图(5)图(4)
1
5
2
3
6
4
A
B
C
D
1
2
34
D
E
A
B
C
l1
l2
1
2
3
1
2
A
G
B
C
E
F
D
【学习目标】
1.进一步巩固平行线的条件和特征,会熟练应用平行线的条件和特征。
2.掌握推理证明的方法。
【使用说明与学法指导】
1.先精读一遍教材P52页。针对课前预习二次阅读教材,并回答问题.
2.找出自己的疑惑和需要讨论的问题,随时记录在课本或导学案上,准备课上讨论质疑.
【课前预习】
1.平行线的判定:(1)_________
__,两直线平行.
(2)________
___,两直线平行.
(3)________
___,两直线平行.
(4)平行于同一条直线的两条直线
.
2.平行线的性质:(1)两直线平行,___
___
_____.
(2)两直线平行,_____
______.
(3)两直线平行,_____
______.
【课堂探究】
一、平行线的条件和特征的几何语言表述
1.如图(1),完成下列解答过程:
(1)∵∠3=______(已知)
∴//(
,两直线平行)
(2)∵∠3=______(已知)
∴//(________
__,两直线平行)
图(1)
(3)∵∠3+______=180°(已知)
∴//(
,两直线平行)
(4)∵//
(已知)
∴∠5=______(两直线平行,
)
(5)∵//
(已知)
∴∠5=______(两直线平行,
)
(6)
∵//
(已知)
∴∠5+______=180°(两直线平行,
)
二、
平行线的条件和特征的综合应用
2.如图(2),直线//,∠3=85°,求∠1.∠2的度数。
图(2)
3.如图(3),已知AB//CD,BE//CF,∠1与∠2相等吗?为什么?
图(3)
【学习小结】
1.判定两直线平行的条件是怎样的?结合图形回答。
2.平行线的性质是怎样的?结合图形回答。
【课堂检测】
1.如图(5),下列推理错误的是(
)
A.∵∠1=∠2,
∴∥b
B.∵∠1=∠3,
∴∥b
C.∵∠3=∠5,
∴c∥d
D.∵∠2+∠4=180°,∴c∥d
2.如图(6),在下列四组条件中,能判定AB∥CD的是(
)
A.∠1=∠2
B.∠3=∠4
C.∠BAD+∠ABC=180°
D.∠ABD=∠BDC
3.如图(7),AB∥CD,AF分别交AB.CD于A.C,CE平分∠DCF,∠1=100°,
则∠2=
4.如图(8),AB⊥EF,CD⊥EF,∠1=∠F=45°,那么与∠FCD
相等的角有_______个,它们分别是___________________________。
图(6)
图(7)
图(8)
4.如图,∠CAB=100°,∠ABF=130°,AC∥MD,BF∥ME,求∠DME
的度数。
5.如图,已知∠1=∠2,∠3=115°。求∠4的度数。
6.如图(10),已知A.B.C三点在同一直线上,∠1=∠2,∠3=∠D。试说明:BD//CE。
【巩固作业】
1.如图(1),∥,∠1=120°,∠2=100°,则∠3=
(
)
A.20°
B.40°
C.50°
D.60°
2.如图(2),下列推理中正确的是(
)
A.
∴
B.
∴
C.
∴
D.
∴
3.下列说法正确的是(
)
A.相等的角是对顶角
B.一对同旁内角的平分线互相垂直
C.对顶角的平分线在一条直线上
D.同位角相等
图(1)
图(2)
图(3)
4.若
,则它的余角是_________,它的补角是________.
5.若∠α与∠β是对顶角,且∠α+∠β=1200
,则∠α=
,∠β=
.
6.如图(3),,若,则=
.
7.已知,如图,EF∥BC,∠A=∠D,∠AOB=70°,∠1+∠C=150°,求∠B的度数.
8、如图,已知AB∥CD,∠α=450,∠D=∠C.你能求出∠D、∠C和∠B的度数吗?
9.已知:某品牌不锈钢锥体的平面图如图所示,设计要求是AB∥CD,且∠A=∠C=143°,请你帮设计师计算一下∠E的度数,并说明理由.
10.
如图,∠1=∠2,∠C=∠D,那么∠A=∠F,为什么?
11.
如图,已知:AB∥CD,AE平分∠BAC,CE平分∠ACD,请说明:AE⊥CF.
4
图(5)图(4)
1
5
2
3
6
4
A
B
C
D
1
2
34
D
E
A
B
C
l1
l2
1
2
3
1
2
A
G
B
C
E
F
D
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
