陕西省黄陵中学高新部2016-2017学年高二下学期期末考试数学(理)试题 Word版含答案
文档属性
| 名称 | 陕西省黄陵中学高新部2016-2017学年高二下学期期末考试数学(理)试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 280.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-18 20:24:51 | ||
图片预览


文档简介
高新部高二期末考试理科数学试题
一、选择题:(本题共12小题,每小题5分,共60分.)
1.若复数z的共轭复数,则复数z的模长为(
)
A.2
B.-1
C.5
D.
2.下列命题正确的是(
)
A.命题“,使得x2-1<0”的否定是:,均有x2-1<0.
B.命题“若x=3,则x2-2x-3=0”的否命题是:若x≠3,则x2-2x-3≠0.
C.“(k∈Z)”是“”的必要而不充分条件.
D.命题“cosx=cosy,则x=y”的逆否命题是真命题.
3.下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,均值与方差都不变;
②设有一个回归方程,变量x增加一个单位时,y平均增加3个单位;
③线性回归方程必经过点(,);
④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说现有100人吸烟,那么其中有99人患肺病.
其中错误的个数是(
)
A.0
B.1
C.2
D.3
4.下列说法正确的是( )
A.命题“若x2>1,则x>1”的否命题为“若x2>1,则x≤1”
B.命题“ x0∈R,x02>1”的否定是“ x∈R,x2>1”
C.命题“x≤1是x2+2x﹣3≤0的必要不充分条件”为假命题
D.命题“若x=y,则cosx=cosy”的逆命题为假命题
5.(1﹣)(1+x)5的展开式中项x3的系数为( )
A.7
B.8
C.10
D.5
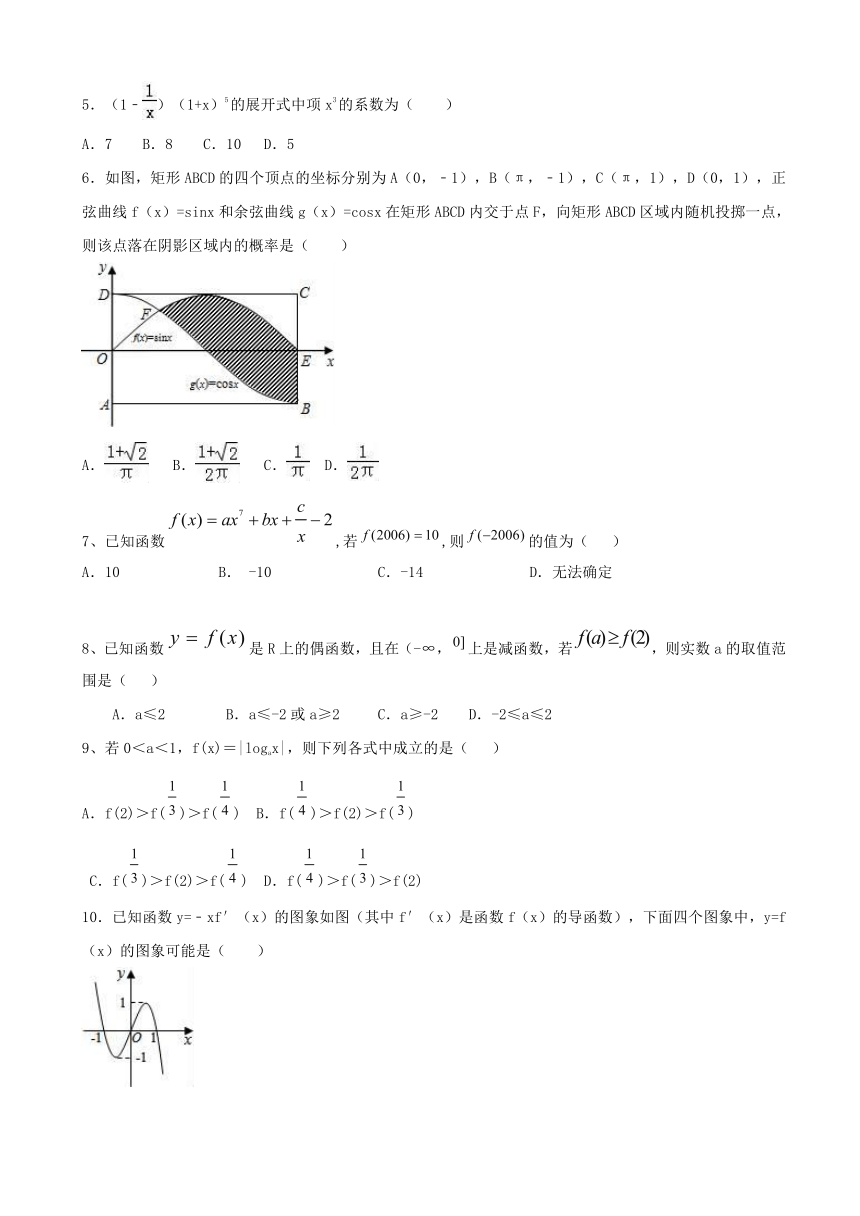
6.如图,矩形ABCD的四个顶点的坐标分别为A(0,﹣1),B(π,﹣1),C(π,1),D(0,1),正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是( )
A.
B.
C.
D.
7、已知函数,若,则的值为(
)
A.10
B.
-10
C.-14
D.无法确定
8、已知函数是R上的偶函数,且在(-∞,上是减函数,若,则实数a的取值范围是(
)
A.a≤2 B.a≤-2或a≥2
C.a≥-2 D.-2≤a≤2
9、若0<a<1,f(x)=|logax|,则下列各式中成立的是(
)
A.f(2)>f()>f()
B.f()>f(2)>f()
C.f()>f(2)>f()
D.f()>f()>f(2)
10.已知函数y=﹣xf′(x)的图象如图(其中f′(x)是函数f(x)的导函数),下面四个图象中,y=f(x)的图象可能是( )
A.
B.
C.
D.
11.已知点P在曲线y=上,α为曲线在点P处的切线的倾斜角,则α的取值范围是( )
A.[0,)
B.
C.
D.
12.O为坐标原点,F为抛物线C:y2=4x的焦点,P为C上一点,若∠OFP=120°,S△POF=( )
A.
B.2
C.或
D.
二、填空题:(本题共4小题,每小题5分,共20分.)
13.曲线在点处的切线方程为
.
14.已知随机变量服从正态分布,且,则
.
15.的二项展开式中的系数是
.(用数字作答)
16.若规定的子集为的第个子集,其中,则E的第211个子集是
.
三、解答题:(本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17.(12分)设函数f(x)=2x3+3ax2+3bx+8在x=1及x=2时取得极值.
(1)求a,b的值;
(2)求曲线f(x)在x=0处的切线方程.
18、(12分)
用反证法证明:如果,那么.
19、(12分)
如图,几何体是圆柱的一部分,它是由矩形(及其内部)以边所在直线为旋转轴旋转得到的,是的中点.
(Ⅰ)设是上的一点,且,求的大小;
(Ⅱ)当,,求二面角的大小.
20.(12分)已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(Ⅰ)求a,b,c,d的值;
(Ⅱ)若对于任意x∈R,都有f(x)≥k﹣g(x)恒成立,求k的取值范围.
21.(12分)
在直角坐标系xOy中,曲线C的参数方程为(θ为参数),直线l的参数方程为
.
(1)若a= 1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为,求a.
22.(10分)
已知函数f(x)=–x2+ax+4,g(x)=│x+1│+│x–1│.
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[–1,1],求a的取值范围.
参考答案与试题解析
一、选择题:(本题共12小题,每小题5分,共60分.)
1.D
2.B
3.D
4.D. 5.D.6.B.7.C
8.B
9.D
10.B.11.D.12.A.
二、填空题:(本题共4小题,每小题5分,共20分.)
13.
14.
15.
40
16.
三、解答题:(本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17解:(1)∵函数f(x)=2x3+3ax2+3bx+8c,
∴f′(x)=6x2+6ax+3b,
∵函数f(x)在x=1及x=2取得极值,∴f′(1)=0,f′(2)=0.
即,
解得a=﹣3,b=4;
(2)由(1)得f(x)=2x3﹣9x2+12x+8,f′(x)=6x2﹣18x+12,
∴f(0)=0,f′(0)=12.∴切线的斜率k=12.切点为(0,8)
由直线方程的点斜式得切线方程为:y﹣8=12x,即12x﹣y+8=0.
18.
(本小题满分12分)
证明:假设则……………………………………………2分
容易看出………………………………………………………………………4分
下面证明……………………………………………………………………5分
因为所以即,从而,…………………………………8分
变形得………………………………………………………………………9分
综上得……………………………………………………………………………10分
这与条件矛盾.……………………………………………………………………11分
因此,假设不成立,即原命题成立.……………………………………………………12分
19.(本小题满分12分)
解
(Ⅰ)因为,,
,平面,,
所以平面,……………………………………………………………………2分
又平面,…………………………………………………………………………3分
所以,又,
因此…………………………………………………………………………4分
(Ⅱ)以为坐标原点,分别以,,所在的直线为,,轴,建立如图所示的空间直角坐标系.由题意得,,,故,,,……………………………………6分
设是平面的一个法向量.
由可得
取,可得平面的一个法向量.………………………………8分
设是平面的一个法向量.
由可得
取,可得平面的一个法向量.…………………………10分
所以.
因此所求的角为.………………………………………………………………………12分
20.
解:(Ⅰ)由题意知f(0)=2,g(0)=2,f′(0)=4,g′(0)=4,
而f′(x)=2x+a,g′(x)=ex(cx+d+c),故b=2,d=2,a=4,d+c=4,
从而a=4,b=2,c=2,d=2;
(Ⅱ)由(I)知,f(x)=x2+4x+2,g(x)=2ex(x+1),
由f(x)≥k﹣g(x)恒成立得f(x)+g(x)≥k恒成立,
设F(x)=f(x)+g(x)=2ex(x+1)+x2+4x+2,
则F′(x)=2ex(x+2)+2x+4=2(x+2)(ex+1),
由F′(x)>0得x>﹣2,由F′(x)<0得x<﹣2,
即当x=﹣2时,F(x)取得极小值,同时也是最小值,
此时F(﹣2)=2e﹣2(﹣2+1)+(﹣2)2+4×(﹣2)+2=﹣2e﹣2﹣2,
则k≤﹣2e﹣2﹣2.
21解:(1)曲线的普通方程为.
当时,直线的普通方程为.
由解得或.
从而与的交点坐标为,.
(2)直线的普通方程为,故上的点到的距离为
.
当时,的最大值为.由题设得,所以;
当时,的最大值为.由题设得,所以.
综上,或.、
22解:(1)当时,不等式等价于.①
当时,①式化为,无解;
当时,①式化为,从而;
当时,①式化为,从而.
所以的解集为.
(2)当时,.
所以的解集包含,等价于当时.
又在的最小值必为与之一,所以且,得.
所以的取值范围为.
一、选择题:(本题共12小题,每小题5分,共60分.)
1.若复数z的共轭复数,则复数z的模长为(
)
A.2
B.-1
C.5
D.
2.下列命题正确的是(
)
A.命题“,使得x2-1<0”的否定是:,均有x2-1<0.
B.命题“若x=3,则x2-2x-3=0”的否命题是:若x≠3,则x2-2x-3≠0.
C.“(k∈Z)”是“”的必要而不充分条件.
D.命题“cosx=cosy,则x=y”的逆否命题是真命题.
3.下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,均值与方差都不变;
②设有一个回归方程,变量x增加一个单位时,y平均增加3个单位;
③线性回归方程必经过点(,);
④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说现有100人吸烟,那么其中有99人患肺病.
其中错误的个数是(
)
A.0
B.1
C.2
D.3
4.下列说法正确的是( )
A.命题“若x2>1,则x>1”的否命题为“若x2>1,则x≤1”
B.命题“ x0∈R,x02>1”的否定是“ x∈R,x2>1”
C.命题“x≤1是x2+2x﹣3≤0的必要不充分条件”为假命题
D.命题“若x=y,则cosx=cosy”的逆命题为假命题
5.(1﹣)(1+x)5的展开式中项x3的系数为( )
A.7
B.8
C.10
D.5
6.如图,矩形ABCD的四个顶点的坐标分别为A(0,﹣1),B(π,﹣1),C(π,1),D(0,1),正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是( )
A.
B.
C.
D.
7、已知函数,若,则的值为(
)
A.10
B.
-10
C.-14
D.无法确定
8、已知函数是R上的偶函数,且在(-∞,上是减函数,若,则实数a的取值范围是(
)
A.a≤2 B.a≤-2或a≥2
C.a≥-2 D.-2≤a≤2
9、若0<a<1,f(x)=|logax|,则下列各式中成立的是(
)
A.f(2)>f()>f()
B.f()>f(2)>f()
C.f()>f(2)>f()
D.f()>f()>f(2)
10.已知函数y=﹣xf′(x)的图象如图(其中f′(x)是函数f(x)的导函数),下面四个图象中,y=f(x)的图象可能是( )
A.
B.
C.
D.
11.已知点P在曲线y=上,α为曲线在点P处的切线的倾斜角,则α的取值范围是( )
A.[0,)
B.
C.
D.
12.O为坐标原点,F为抛物线C:y2=4x的焦点,P为C上一点,若∠OFP=120°,S△POF=( )
A.
B.2
C.或
D.
二、填空题:(本题共4小题,每小题5分,共20分.)
13.曲线在点处的切线方程为
.
14.已知随机变量服从正态分布,且,则
.
15.的二项展开式中的系数是
.(用数字作答)
16.若规定的子集为的第个子集,其中,则E的第211个子集是
.
三、解答题:(本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17.(12分)设函数f(x)=2x3+3ax2+3bx+8在x=1及x=2时取得极值.
(1)求a,b的值;
(2)求曲线f(x)在x=0处的切线方程.
18、(12分)
用反证法证明:如果,那么.
19、(12分)
如图,几何体是圆柱的一部分,它是由矩形(及其内部)以边所在直线为旋转轴旋转得到的,是的中点.
(Ⅰ)设是上的一点,且,求的大小;
(Ⅱ)当,,求二面角的大小.
20.(12分)已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(Ⅰ)求a,b,c,d的值;
(Ⅱ)若对于任意x∈R,都有f(x)≥k﹣g(x)恒成立,求k的取值范围.
21.(12分)
在直角坐标系xOy中,曲线C的参数方程为(θ为参数),直线l的参数方程为
.
(1)若a= 1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为,求a.
22.(10分)
已知函数f(x)=–x2+ax+4,g(x)=│x+1│+│x–1│.
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[–1,1],求a的取值范围.
参考答案与试题解析
一、选择题:(本题共12小题,每小题5分,共60分.)
1.D
2.B
3.D
4.D. 5.D.6.B.7.C
8.B
9.D
10.B.11.D.12.A.
二、填空题:(本题共4小题,每小题5分,共20分.)
13.
14.
15.
40
16.
三、解答题:(本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17解:(1)∵函数f(x)=2x3+3ax2+3bx+8c,
∴f′(x)=6x2+6ax+3b,
∵函数f(x)在x=1及x=2取得极值,∴f′(1)=0,f′(2)=0.
即,
解得a=﹣3,b=4;
(2)由(1)得f(x)=2x3﹣9x2+12x+8,f′(x)=6x2﹣18x+12,
∴f(0)=0,f′(0)=12.∴切线的斜率k=12.切点为(0,8)
由直线方程的点斜式得切线方程为:y﹣8=12x,即12x﹣y+8=0.
18.
(本小题满分12分)
证明:假设则……………………………………………2分
容易看出………………………………………………………………………4分
下面证明……………………………………………………………………5分
因为所以即,从而,…………………………………8分
变形得………………………………………………………………………9分
综上得……………………………………………………………………………10分
这与条件矛盾.……………………………………………………………………11分
因此,假设不成立,即原命题成立.……………………………………………………12分
19.(本小题满分12分)
解
(Ⅰ)因为,,
,平面,,
所以平面,……………………………………………………………………2分
又平面,…………………………………………………………………………3分
所以,又,
因此…………………………………………………………………………4分
(Ⅱ)以为坐标原点,分别以,,所在的直线为,,轴,建立如图所示的空间直角坐标系.由题意得,,,故,,,……………………………………6分
设是平面的一个法向量.
由可得
取,可得平面的一个法向量.………………………………8分
设是平面的一个法向量.
由可得
取,可得平面的一个法向量.…………………………10分
所以.
因此所求的角为.………………………………………………………………………12分
20.
解:(Ⅰ)由题意知f(0)=2,g(0)=2,f′(0)=4,g′(0)=4,
而f′(x)=2x+a,g′(x)=ex(cx+d+c),故b=2,d=2,a=4,d+c=4,
从而a=4,b=2,c=2,d=2;
(Ⅱ)由(I)知,f(x)=x2+4x+2,g(x)=2ex(x+1),
由f(x)≥k﹣g(x)恒成立得f(x)+g(x)≥k恒成立,
设F(x)=f(x)+g(x)=2ex(x+1)+x2+4x+2,
则F′(x)=2ex(x+2)+2x+4=2(x+2)(ex+1),
由F′(x)>0得x>﹣2,由F′(x)<0得x<﹣2,
即当x=﹣2时,F(x)取得极小值,同时也是最小值,
此时F(﹣2)=2e﹣2(﹣2+1)+(﹣2)2+4×(﹣2)+2=﹣2e﹣2﹣2,
则k≤﹣2e﹣2﹣2.
21解:(1)曲线的普通方程为.
当时,直线的普通方程为.
由解得或.
从而与的交点坐标为,.
(2)直线的普通方程为,故上的点到的距离为
.
当时,的最大值为.由题设得,所以;
当时,的最大值为.由题设得,所以.
综上,或.、
22解:(1)当时,不等式等价于.①
当时,①式化为,无解;
当时,①式化为,从而;
当时,①式化为,从而.
所以的解集为.
(2)当时,.
所以的解集包含,等价于当时.
又在的最小值必为与之一,所以且,得.
所以的取值范围为.
同课章节目录
