数学六年级下人教版6.1比和比例课件(62张)
文档属性
| 名称 | 数学六年级下人教版6.1比和比例课件(62张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-18 09:52:22 | ||
图片预览










文档简介
(共61张PPT)
`
复习目标
1、熟练掌握比和比例的意义及基本性质。
2、能熟练的掌握化简比和求比值。
3、理解比例的基本性质,能熟练的解比例。
4、掌握比例尺的意义,并解答相关的比例尺的应用题。
5、正确判断正比例、反比例关系,并能解答正、反比例应用题。
相关概念考查
什么是比? 比的基本性质
比例的意义是什么? 什么是比例的基本性质
比和除法、分数之间的关系?三者关系用字母怎样表示?
什么是化简比? 怎样求比值
怎样判断两个比成比例
怎样利用比和比例知识解决生活问题?
★比和比例的意义与基本性质★
比 比例
意义
各部分名称
基本性质
两个数相除又叫两个数的比。
表示两个比相等的式子叫做比例。
0.9 ︰ 0.6 = 1.5
↓ ↓ ↓
( )( )( )
比的前项和后项同时乘上或除以相同的数(0除外),比值不变。
在比例里,两个内项的积等于两个外项的积。
5︰6 = 20︰24
外项
内项
前项
后项
比值
1. 0.9︰0.6 =(0.9×10)︰(0.6×10)
= 9︰6
=(9÷3)︰(6÷3)
= 3︰2
例如:
2. 5 ︰6 = 20︰24
6×20
5×24
=
比的基本性质
比例的基本性质
各类比赛中的比不是我们这节课学习的比,它只是一种计分形式,是比较大小的,是相差关系,不是相除关系。
中国 :日本
4 :0
辨一辨:
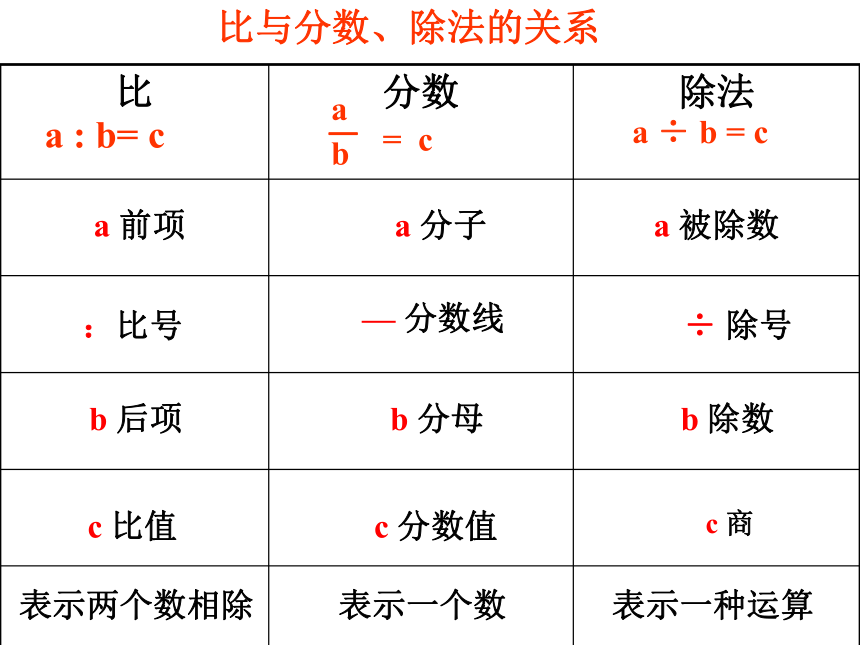
比与分数、除法的关系
比 分数 除法
a : b= c
-
b
a
= c
a ÷ b = c
a 前项
a 分子
a 被除数
:比号
— 分数线
÷ 除号
b 后项
b 分母
b 除数
c 比值
c 分数值
c 商
表示两个数相除
表示一个数
表示一种运算
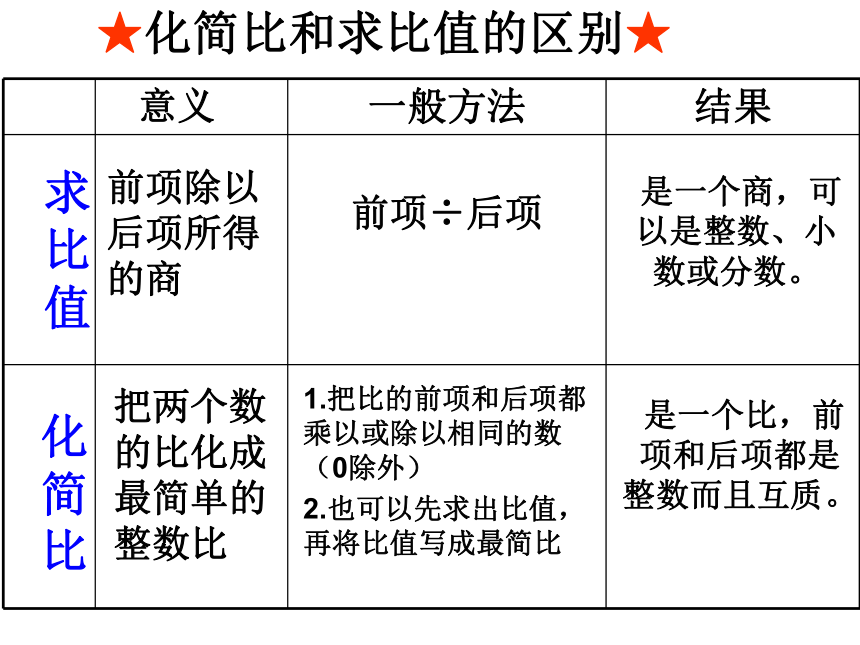
★化简比和求比值的区别★
一般方法 结果
前项÷后项
是一个商,可以是整数、小数或分数。
1.把比的前项和后项都乘以或除以相同的数(0除外)
2.也可以先求出比值,再将比值写成最简比
是一个比,前项和后项都是整数而且互质。
求比值
化简比
前项除以后项所得的商
把两个数的比化成最简单的整数比
意义
注 意
1.当是同类量的两个数相比,前项与后项单位不同时,要先化成相同的单位,然后再求比值或化简比。
例如:0.5米:20厘米=50厘米:20厘米
=—=—
2.当不是同类量的两个数相比时,前项直接除以后项即可。
如:一列客车2小时行驶120千米,则客车所行路程与时间的比是60:1
50
20
5
2
解比例
根据比例的基本性质,如果已经知道比例中的任何三项,就可以求出另外一个未知项。
在比例中,两个外项的积等于两个内项的积。
利用你喜欢的方法判断下列哪组中的两个比是否可以组成比例,并把它写出来。
6:3和8:5 0.2:2.5和4:50
—:—和—:— 1.4:2和7:10
2
1
5
1
8
5
4
1
可以利用求比值和比例的基本性质 (假设法)来判断两个比是否可以组成比例。
0.4:x=1.2:2 =
解:1.2 =0.4×2
1.2 =0.8
=0.8÷1.2
=
3
2
解: =
=2
54
3×36
当堂训练1
1、解比例
0.25:x=15:100 :x=0.3:0.5
2、化简下列各比并求比值:
3.6:1.4 2 — :0.8 1— :0.8
500千克:2— 吨 1米10厘米:15分米 —日 :12时
7
1
8
1
2
1
8
7
当堂训练1
3、一项工作,甲乙合作需20天完成,已知甲乙效率的比是4:5,甲乙两队单独完成各需要多少天?
4、甲是乙的 ,丙是乙的 ,甲:乙:丙=( )
思考题
5、某工厂由1240人,女职工的 与男职工 同样多,那么男、女职工各有多少人?
两个绳子一共长15.2米,如果第一根绳子增加它的 ,第二根绳子减少它的 ,则两根绳子一样长。球第一根绳子原来多长?
1、填空
(1)在a:7=9:b中,( )是内项,( )是
外项,a×b=( )。
(2)一个比例的两个内项分别是3和8,则两个外项的
积是( ),两个外项可能是( )和( )。
(3)在一个比例里,两个外项互为倒数,那么两个内
项的积是( ),如果一个外项是 ,另一个
外项是( )。
7、9
a、b
63
24
1
综 合 练 习
4
6
9
(4)在比例里,两个内项的积是18,其中一个外
项是2,另一个外项是( )。
(5)如果5a=3b,那么, = , = 。
5
3
3
5
(6)小圆的半径是2厘米,大圆的半径是3厘米,
大圆和小圆的周长比是( )。
(7)甲、乙两数的比是5 :3,乙数是60,甲数是
( )。
3:2
100
(8)若A×5=B×6,则A:B=( ):( )。
(9)9:3=36:12如果第三项减去12,等号左边不
变,那么第四项应减去( )。
(10)用5、2、15、6四个数组成两个比例:
( )=( )、
( )=( )。
6
5
4
5:2
15:6
6:2
15:5
2、判断
(1)在比例中,两个外项的积减去两个
内项的积,差是0。( )
(2)18:30和3:5可以组成比例。( )
(3)如果4X=3Y,(X和Y均不为0),
那么4:X=3:Y。( )
(4)因为3×10=5×6,所以3:5=10:6。( )
√
√
×
×
3、选择题
(1) 9︰6的比值是( )
(A)3 ︰ 2 (B) 1— (C) 2 ︰ 3
(2) ——的最简比是( )
(A)300 ︰ 1 (B)300 (C) 1︰ 300
(3) 0.25 ︰1.25的最简比是( )
(A)25 ︰ 125 (B)1︰ 5 (C) 5︰ 1
1
2
9
0.03
B
A
B
1、六年级班男生人数与女生人数的比是4 ∶5。
男生人数是女生人数的( ),
女生人数是男生人数的( ),
男生人数是全班总人数的( ),
女生人数是全班总人数的( )。
男生人数比女生人数少( ),
女生人数比男生人数多( ),
4、填空题
2、生产一批零件,甲单独做6小时完成,乙单独做8小时完成。
(1)甲完成任务的时间与乙完成任务的时间
的最简比是( ) ︰ ( )
(2)甲的工作效率与乙的工作效率的最简比
是( ) ︰ ( )
(3)乙的工作效率与甲的工作效率的最简比
是( ) ︰ ( )
3 4
3 4
4 3
3、把10g糖放入100g水中,糖与水的比是( );糖与糖水的比是( );水与糖水的比是( )。
1:10
1:11
10:11
2:1
2
4
25
1.5
4、甲数和乙数的比是5:4,甲数是20,乙数是( )。
16
7、比的前项扩大3倍,后项缩小3倍,比值( )。
扩大9倍
8、甲数和乙数的比是5:8,则甲数比乙数少( ),乙数比甲数多( )。
1、一个长方形,周长40cm,长和宽的比例是3:2。这个长方形的面积是多少?
(3+2)×2=10
40÷10=4(cm)
长:4×3=12(cm)
宽:4×2=8(cm)
面积:12×8=96(cm2)
答:这个长方形的面积是96cm2。
5、应用题
解:设长方形的长为3xcm,宽为2xcm
根据题意可得:
2×(3x+2x)=40
10x=40
x=4
故长方形的长=3 ×4=12cm
宽=2 ×4=8cm
面积=长×宽
=12 ×8
96cm2
解:设甲乙两地相距X千米。
答:甲乙两地相距150km。
2、王叔叔开车从甲地到乙地,前2小时行了100km。照这样的速度,从甲地到乙地一共要用3小时,甲乙两地相距多远?
100÷2=50(km/小时)
50×3=150(km)
解:设返回时用了X小时。
答:返回时用了2.5小时。
3、王叔叔开车从甲地到乙地一共用了3小时,每小时行50km。返回时每小时行60km,返回时用了多长时间?
50×3=150(km)
150÷60=2.5(小时)
4、用一台打字机打字,6小时打36页,照这样计算,如果再打4小时,一共可以打字多少页?
解:设一共可以打字X页。
答:一共可以打字60页。
36÷6=6(页/小时)
6×4=24(页)
36+24=60(页)
5、工人们安装一批电线杆,每天安装12根,30天可以完成。如果每天多安装6根,几天能够完成?
解:设X天可以完成。
答:20天可以完成。
12×30=360(根)
12+6=18(根)
360÷18=20(天)
6
李阿姨是剪纸艺人。平时李阿姨每天工作6小时,剪出72张纸;节日期间,李阿姨每天要工作8小时,能剪出96张剪纸。
(1)写出李阿姨平时和节日期间剪纸张数及相应工作时间的比。
(2)上面两个比能组成比例吗?为什么?
(3)如果李阿姨要剪出120张剪纸,需要多少小时?
平时:72:6
节日期间:96:8
复习目标
1、熟练掌握比和比例的意义及基本性质。
2、能熟练的掌握化简比和求比值。
3、理解比例的基本性质,能熟练的解比例。
4、掌握比例尺的意义,并解答相关的比例尺的应用题。
5、正确判断正比例、反比例关系,并能解答正、反比例应用题。
相关概念考查
什么是比例尺?
比例尺的应用
按比例分配问题的解题方法是什么?
什么是正、反比例?
怎样判断两个相关联的量成正比例或反比例?
如何应用正、反比例解生活问题?
比例尺
1、比例尺的意义
一幅图的图上距离和实际距离的比叫做比例尺,即
图上距离:实际距离=比例尺
比例尺没有单位
2、比例尺的分类
(1)按表现形式,可以分为数值比例尺和线段比例尺
(2)按将实际距离放大还是缩小分,分为缩小比例尺和放大比例尺。
3、应用比例尺画图
(1)确定比例尺
(2)根据比例尺求出图上距离
(3)画图
(4)标出实际距离和比例尺
比例尺的应用:
根据图上距离:实际距离=比例尺,得到:
①已知图上距离和实际距离,求比例尺?
比例尺=图上距离÷实际距离
②已知图上距离和比例尺,求实际距离?
实际距离=图上距离÷比例尺
③已知实际距离和比例尺,求图上距离
图上距离=实际距离×比例尺
练习题
2、在比例尺是1:100的平面图上量的一间教室长7厘米,宽6厘米,这间教室占地面积是多少平方厘米?
0 10 20 30米
看着这个线段比例尺,你能理解
它的意思吗?说说看。
1、
图形的放大与缩小
1、图形的放大与缩小的特点是:形状相同,大小不同
2、图形的放大或缩小的方法:
一看,二算,三画
练习题
1、 A城到B城的实际距离是12km,画在比例尺为
1:100000的图纸上,应画多少厘米?
2、一个长5cm,宽3cm的长方形按3︰1
放大,得到的图形的周长的是多少厘米?
面积是多少平方厘米?
练习:
1 、一副地图中某两地的图上距离是5cm,
表示实际距离15km,这幅地图的比例尺是
( )。
2 、比例尺1 ︰2000000改写成线段比例尺
是( )。
D
1 ︰300000
3、在比例尺是1︰5000000的云南地图上,量得大理到楚雄的距离是3.2厘米。计算一下,大理到楚雄的实际距离大约是多少千米?
答:大理到楚雄的实际距离大约是160km。
4、在一张1:500的设计图纸上,量得一正方形建筑的边长是20cm,这个建筑物的实际占地面积是多少平方米?
(1)求边长的实际距离:
(2)求建筑物实际占地面积:
1002 = 10000(m2)
答:这个建筑物的实际占地面积是10000m2。
5、修建一个长80m、宽60m的长方形操场,用1:1000的比例尺画在图纸上,长和宽各画多少cm?
(1)求长的图上距离:
80m=8000cm
(2)求宽的图上距离:
60m=6000cm
答:长画8cm,宽画6cm。
按比例分配:
①按比例分配问题的特征是什么?
用比或者连比反映各部分占总数量的份数,或者直接给出各部分占总数量的份数。
如:一个三角形三个内角度数比是1:2:3
②按比例分配问题与平均数问题的区别是什么?
按比例分配不一定是等分,即平均分
③按比例分配问题解题方法?
(1)找出或求出要分的总数;
(2)根据已知的比求总份数;
(3)按照要分配的各部分占总数的几分之几,分别求出每一部分是多少,还可以先求出每一份,再以它为标准,分别求出各部分是多少。
练习题
1、一个三角形三个内角度数比是1:2:3,这个三角形的三个内角分别是多少?
2、做个长方体模型,共需要96米长的铁丝,这个长方体的长宽高的比是1:2:3,则这个长方体的长宽高分别是多少
该长方体的表面积是多少平方米?
体积是多少?
正比例和反比例的意义
1、成正比例的量
①两种相关联的量②一种量变化,另一种量也随着变化③比值一定
关系式:
2、成反比例的量
①两种相关联的量②一种量变化,另一种量也随着变化③积一定
关系式: x y= k (一定)
3、判断两种量成正比例还是成反比例的方法。
关键是看这两种相关联的量对应的两个数的商一定还是积一定,如果商一定就成正比例,如果积一定就成反比例。
(一定)
成正比例的量和成反比例的量有什么共同点和不同点?
正比例关系 反比例关系
相同点
变化情况
一定
关系式
变化图像
不同点
正比例关系 反比例关系
不
同
点 变化情况
一定
变化图像
比值或商
乘积
关系式
相同点
两种相关联的量,一种量随着另一种量的变化而变化。
一种量扩大(缩小),另一种量也扩大(缩小)
一种量扩大(缩小),另一种量反而缩小(扩大)
=k(一定)
X×Y=K(一定)
练习
下面各题中的两种量是不是成比例 如果成比例,成什么比例关系
(1)比例尺一定,两地的实际距离和图上距离。
(2)被除数一定,除数和商。
(3)梯形的上底和下底不变,梯形的面积和高。
(4)如果y=5x,y和x。
判断正、反比例的三个注意点
第一,注意不要被假象所迷惑。成正反比例量的特点是一个量变化,另一个量也随着变化,但仅凭此不能确定两个量是否成比例。
如:“圆的半径和面积”,表面看,圆的半径扩大或缩小,圆的面积也随着扩大或缩小,似乎成正比例,但实际上圆面积=圆半径×π ×圆半径,而π ×圆半径也是一个变量,所以圆的半径和面积不成正比例。
第二,注意不要忽略隐藏着的量。有些判断中,虽没有明确表达定量,但不能认为它一定不成比例,有可能它的定量隐含其中。
如:“订阅《中小学生报》的份数和钱数”,题中没有说出定量,但我们分析一下就可知道,钱数=份数×每份的价钱,因为订阅的是同一份报纸,它的单价是一定的,所以订阅《小学生报》的份数和钱数成正比例。
判断正、反比例的三个注意点
第三,注意不要被常量所干扰。有些判断中,可能会涉及固定的数值,也就是我们所说的常量,往往会给我们的判断增加难度,我们不能被其干扰。
如:“三角形的面积一定,它的底和高成反比例”,因为三角形的面积=底×高÷2,所以底×高=三角形面积×2,三角形的面积一定,面积的2倍也是一个定量,所以三角形面积一定,它的底和高成反比例。
怎么解正、反比例应用题:
①正、反比例应用题的特征?
②解正、反比例应用题一般方法和步骤?
练习题: 1、一台拖拉机16天耕地19.20公顷,30天可以耕地多少公顷
2、制造一批零件,计划每天做160个,15天完成。实际每天超产40个,多少天就能完成这批零件?
3、一个筑路队修一条公路,原计划每天修3.2千米,15天完成,实际每天比原计划多修了25%,实际多少天可以完成?
当堂训练
1、填空:
①一幅地图的线段比例尺是 , 它表示实际距离是图上距离的( )倍。
②)在一个比例里,两个外项的积是最小的质数,一个内项是0.5,另一个内项是( )。
③在 的图纸上,一个正方形的面积为16平方厘米,它的
实际面积是( )平方米。
④一车水果重1.8吨,按2:3:5的比例分配给甲、乙、丙三个水果店,乙水果店分得这批水果的()。
⑤把3克盐放入12克水中,盐与盐水重量的最简整数比是( )。
0
40
80
120千米
当堂训练
二、判断:
1、小麦的出粉率一定,小麦的总重量和面粉的重量成正比例关系。 ( )
2、因为甲数:乙数=25:23,所以甲数=25,乙数=23。 ( )
3、车轮的直径一定,车轮转动的周数和所行路程成正比例。 ( )
4、如果A与B成反比例,B与C也成反比例,那么A与C成正比例。 ( )
5、如果a×3=b×5,那么a:b=5:3。 ( )
6、y=8x,表示x和y成正比例。 ( )
7、半径与直径的比是1:2。 ( )
8、甲地到乙地,甲车要6小时,乙车要8小时,甲车和乙车的速度比是3:4。 ( )
当堂训练
三、选择:
1、把10克糖溶解在100克水中,糖与糖水的比是( )
A、10:1 B、1:10 C、1:11 D、11:1
2、一个圆的直径与周长的比是( )。
A、1:2 B、1: C、2:
3、一批产品,合格产品与不合格产品的比是4:1,这批产品的不合格率是( ) A、25% B、20% C、10%
4、在同一个圆里,周长与直径( )。
A、成正比例 B、成反比例C、不成比例
5、一个三角形内角度数的比是7:2:1,这个三角形( )。A、钝角三角形 B、锐角三角形 C、直角三角形
6、一条长5米的线段画在比例尺是1:100的图中,要比画在比例尺只是1:1000的图中( )。
A、长 B、短 C、一样长
7、两个圆的直径比是1:2,周长比是( )。
A、1:2 B、1:4 C、1:8
当堂训练
四、应用题:
1、一种农药水是用药和水按1:100配成的,要配制这种农药水8080千克,需要药粉多少千克?
2、做一批零件,如果每天做200个,15天可以做完,现在要在12天完成,平均每天做多少个?(比例解)
3、甲地到乙地的公路长392千米。一辆汽车3小时行了168千米。照这样计算,行完全还需要几小时?(比例解)
4、甲乙丙三种商品总价值为5800元。按数量,甲与乙的比是1:2,乙与丙的比是1:2.5;按单价,甲与乙的比是3:2,乙与丙的比是4:3。三种商品各值多少元?
5、在比例尺是1:3000000的地图上,量得两地距离是10厘米,甲乙两车同时从两地相向而行,3小时后两车相遇。已知甲乙两车的速度比是2:3,求甲乙两车的速度各是多少千米?
(6)张师傅加工一批零件,第一天完成的个数与零件的总个数的比是1:3。如果再加工15个,就可以完成这批零件的一半。这批零件共有多少个?
(7)一件工作,甲单独做要用6小时,乙单独做要用4小时。甲做完 后,两人合作,还要几小时才能做完?
(8)一个工厂由于采用新工艺,现在每件产品的成本是37.4元,比原来降低了15%。原来每件产品的成本是多少元?
(9)甲乙两列火车从相距450千米的两地同时相向开出,经过5小时正好相遇。已知甲乙两列火车的速度之比是4 :5,两列火车
每小时各行多少千米?
综合练习
1、填空:
1)一个比例有两个( )项,两个( )项。
2)判断两个比是否能组成比例,可以看它们的( )也可以用( )进行判断。
3)写出比值是2.5的比,并组成比例( )
4)在比例中,如果两个内项的分别是4和5,那么组成
两个外项的两个数的积一定是( )
内
外
5:2=10:4
20
5)甲数是乙数的1-,甲数和乙数的比是( ),比值是( )。
6)( )成= — =( )÷20=0.8=( )℅=( ):60
7)甲数和乙数的比是3:5,甲数占乙数的-,乙数占甲乙两数总数的-。
8)3x=4y,(x、y都不为0),x和 y的比是( ):( )
9)两个数的比值是4,前项和后项同时扩大3倍,比值是( )。
2
1
( )
20
2、选择
3:2
1.5
25
16
80
48
3
5
8
5
4
3
不变
8
1)两和正方形的边长的比是3:5,它们面积的比是( ),周长的比是( )。
A:1:3 B: 3:5 C:1:25 D:9:25
2)把100克白糖放如1000克水中,糖和水的比是( )
A: 1:12 B: 1:11 C: 1:10 D: 1:9
3)比的前项扩大2倍,后项缩小2倍,比值( )
A: 扩大4倍 B: 缩小4倍 C:不变 D: 扩大2倍
4)甲数的-等于乙数的- ,乙数与甲数的比是( )
A : 25:18 B: 18:25 C: 1:2 D: 2:1
5
3
6
5
D
B
C
A
A
5)一个圆柱和圆锥等高等体积,他们的底面积的比是( ) 。
A: 1:3 B: 3:1 C: 1: 9 D: 9:1
3、判断:
1)正方形的面积的比等于边长的比( )
2)如果a:b的比是3:4,3a =4b。( )
3)45分:1-时的比值是0.6。( )
4)-化简后是最简整数比是2-。( )
4
1
4
10
2
1
×
×
×
×
B
5、用21、3 、-、0.125四个数组成比值不同的比例
8
7
4、根据要求写出一个比例式
1)两个外项分别是3和x,两和内项分别是9和12。
2)等号左边的比是x:5,右边比的比值是5。
3)使各项都是整数,且两个比的比值为0.8。
`
复习目标
1、熟练掌握比和比例的意义及基本性质。
2、能熟练的掌握化简比和求比值。
3、理解比例的基本性质,能熟练的解比例。
4、掌握比例尺的意义,并解答相关的比例尺的应用题。
5、正确判断正比例、反比例关系,并能解答正、反比例应用题。
相关概念考查
什么是比? 比的基本性质
比例的意义是什么? 什么是比例的基本性质
比和除法、分数之间的关系?三者关系用字母怎样表示?
什么是化简比? 怎样求比值
怎样判断两个比成比例
怎样利用比和比例知识解决生活问题?
★比和比例的意义与基本性质★
比 比例
意义
各部分名称
基本性质
两个数相除又叫两个数的比。
表示两个比相等的式子叫做比例。
0.9 ︰ 0.6 = 1.5
↓ ↓ ↓
( )( )( )
比的前项和后项同时乘上或除以相同的数(0除外),比值不变。
在比例里,两个内项的积等于两个外项的积。
5︰6 = 20︰24
外项
内项
前项
后项
比值
1. 0.9︰0.6 =(0.9×10)︰(0.6×10)
= 9︰6
=(9÷3)︰(6÷3)
= 3︰2
例如:
2. 5 ︰6 = 20︰24
6×20
5×24
=
比的基本性质
比例的基本性质
各类比赛中的比不是我们这节课学习的比,它只是一种计分形式,是比较大小的,是相差关系,不是相除关系。
中国 :日本
4 :0
辨一辨:
比与分数、除法的关系
比 分数 除法
a : b= c
-
b
a
= c
a ÷ b = c
a 前项
a 分子
a 被除数
:比号
— 分数线
÷ 除号
b 后项
b 分母
b 除数
c 比值
c 分数值
c 商
表示两个数相除
表示一个数
表示一种运算
★化简比和求比值的区别★
一般方法 结果
前项÷后项
是一个商,可以是整数、小数或分数。
1.把比的前项和后项都乘以或除以相同的数(0除外)
2.也可以先求出比值,再将比值写成最简比
是一个比,前项和后项都是整数而且互质。
求比值
化简比
前项除以后项所得的商
把两个数的比化成最简单的整数比
意义
注 意
1.当是同类量的两个数相比,前项与后项单位不同时,要先化成相同的单位,然后再求比值或化简比。
例如:0.5米:20厘米=50厘米:20厘米
=—=—
2.当不是同类量的两个数相比时,前项直接除以后项即可。
如:一列客车2小时行驶120千米,则客车所行路程与时间的比是60:1
50
20
5
2
解比例
根据比例的基本性质,如果已经知道比例中的任何三项,就可以求出另外一个未知项。
在比例中,两个外项的积等于两个内项的积。
利用你喜欢的方法判断下列哪组中的两个比是否可以组成比例,并把它写出来。
6:3和8:5 0.2:2.5和4:50
—:—和—:— 1.4:2和7:10
2
1
5
1
8
5
4
1
可以利用求比值和比例的基本性质 (假设法)来判断两个比是否可以组成比例。
0.4:x=1.2:2 =
解:1.2 =0.4×2
1.2 =0.8
=0.8÷1.2
=
3
2
解: =
=2
54
3×36
当堂训练1
1、解比例
0.25:x=15:100 :x=0.3:0.5
2、化简下列各比并求比值:
3.6:1.4 2 — :0.8 1— :0.8
500千克:2— 吨 1米10厘米:15分米 —日 :12时
7
1
8
1
2
1
8
7
当堂训练1
3、一项工作,甲乙合作需20天完成,已知甲乙效率的比是4:5,甲乙两队单独完成各需要多少天?
4、甲是乙的 ,丙是乙的 ,甲:乙:丙=( )
思考题
5、某工厂由1240人,女职工的 与男职工 同样多,那么男、女职工各有多少人?
两个绳子一共长15.2米,如果第一根绳子增加它的 ,第二根绳子减少它的 ,则两根绳子一样长。球第一根绳子原来多长?
1、填空
(1)在a:7=9:b中,( )是内项,( )是
外项,a×b=( )。
(2)一个比例的两个内项分别是3和8,则两个外项的
积是( ),两个外项可能是( )和( )。
(3)在一个比例里,两个外项互为倒数,那么两个内
项的积是( ),如果一个外项是 ,另一个
外项是( )。
7、9
a、b
63
24
1
综 合 练 习
4
6
9
(4)在比例里,两个内项的积是18,其中一个外
项是2,另一个外项是( )。
(5)如果5a=3b,那么, = , = 。
5
3
3
5
(6)小圆的半径是2厘米,大圆的半径是3厘米,
大圆和小圆的周长比是( )。
(7)甲、乙两数的比是5 :3,乙数是60,甲数是
( )。
3:2
100
(8)若A×5=B×6,则A:B=( ):( )。
(9)9:3=36:12如果第三项减去12,等号左边不
变,那么第四项应减去( )。
(10)用5、2、15、6四个数组成两个比例:
( )=( )、
( )=( )。
6
5
4
5:2
15:6
6:2
15:5
2、判断
(1)在比例中,两个外项的积减去两个
内项的积,差是0。( )
(2)18:30和3:5可以组成比例。( )
(3)如果4X=3Y,(X和Y均不为0),
那么4:X=3:Y。( )
(4)因为3×10=5×6,所以3:5=10:6。( )
√
√
×
×
3、选择题
(1) 9︰6的比值是( )
(A)3 ︰ 2 (B) 1— (C) 2 ︰ 3
(2) ——的最简比是( )
(A)300 ︰ 1 (B)300 (C) 1︰ 300
(3) 0.25 ︰1.25的最简比是( )
(A)25 ︰ 125 (B)1︰ 5 (C) 5︰ 1
1
2
9
0.03
B
A
B
1、六年级班男生人数与女生人数的比是4 ∶5。
男生人数是女生人数的( ),
女生人数是男生人数的( ),
男生人数是全班总人数的( ),
女生人数是全班总人数的( )。
男生人数比女生人数少( ),
女生人数比男生人数多( ),
4、填空题
2、生产一批零件,甲单独做6小时完成,乙单独做8小时完成。
(1)甲完成任务的时间与乙完成任务的时间
的最简比是( ) ︰ ( )
(2)甲的工作效率与乙的工作效率的最简比
是( ) ︰ ( )
(3)乙的工作效率与甲的工作效率的最简比
是( ) ︰ ( )
3 4
3 4
4 3
3、把10g糖放入100g水中,糖与水的比是( );糖与糖水的比是( );水与糖水的比是( )。
1:10
1:11
10:11
2:1
2
4
25
1.5
4、甲数和乙数的比是5:4,甲数是20,乙数是( )。
16
7、比的前项扩大3倍,后项缩小3倍,比值( )。
扩大9倍
8、甲数和乙数的比是5:8,则甲数比乙数少( ),乙数比甲数多( )。
1、一个长方形,周长40cm,长和宽的比例是3:2。这个长方形的面积是多少?
(3+2)×2=10
40÷10=4(cm)
长:4×3=12(cm)
宽:4×2=8(cm)
面积:12×8=96(cm2)
答:这个长方形的面积是96cm2。
5、应用题
解:设长方形的长为3xcm,宽为2xcm
根据题意可得:
2×(3x+2x)=40
10x=40
x=4
故长方形的长=3 ×4=12cm
宽=2 ×4=8cm
面积=长×宽
=12 ×8
96cm2
解:设甲乙两地相距X千米。
答:甲乙两地相距150km。
2、王叔叔开车从甲地到乙地,前2小时行了100km。照这样的速度,从甲地到乙地一共要用3小时,甲乙两地相距多远?
100÷2=50(km/小时)
50×3=150(km)
解:设返回时用了X小时。
答:返回时用了2.5小时。
3、王叔叔开车从甲地到乙地一共用了3小时,每小时行50km。返回时每小时行60km,返回时用了多长时间?
50×3=150(km)
150÷60=2.5(小时)
4、用一台打字机打字,6小时打36页,照这样计算,如果再打4小时,一共可以打字多少页?
解:设一共可以打字X页。
答:一共可以打字60页。
36÷6=6(页/小时)
6×4=24(页)
36+24=60(页)
5、工人们安装一批电线杆,每天安装12根,30天可以完成。如果每天多安装6根,几天能够完成?
解:设X天可以完成。
答:20天可以完成。
12×30=360(根)
12+6=18(根)
360÷18=20(天)
6
李阿姨是剪纸艺人。平时李阿姨每天工作6小时,剪出72张纸;节日期间,李阿姨每天要工作8小时,能剪出96张剪纸。
(1)写出李阿姨平时和节日期间剪纸张数及相应工作时间的比。
(2)上面两个比能组成比例吗?为什么?
(3)如果李阿姨要剪出120张剪纸,需要多少小时?
平时:72:6
节日期间:96:8
复习目标
1、熟练掌握比和比例的意义及基本性质。
2、能熟练的掌握化简比和求比值。
3、理解比例的基本性质,能熟练的解比例。
4、掌握比例尺的意义,并解答相关的比例尺的应用题。
5、正确判断正比例、反比例关系,并能解答正、反比例应用题。
相关概念考查
什么是比例尺?
比例尺的应用
按比例分配问题的解题方法是什么?
什么是正、反比例?
怎样判断两个相关联的量成正比例或反比例?
如何应用正、反比例解生活问题?
比例尺
1、比例尺的意义
一幅图的图上距离和实际距离的比叫做比例尺,即
图上距离:实际距离=比例尺
比例尺没有单位
2、比例尺的分类
(1)按表现形式,可以分为数值比例尺和线段比例尺
(2)按将实际距离放大还是缩小分,分为缩小比例尺和放大比例尺。
3、应用比例尺画图
(1)确定比例尺
(2)根据比例尺求出图上距离
(3)画图
(4)标出实际距离和比例尺
比例尺的应用:
根据图上距离:实际距离=比例尺,得到:
①已知图上距离和实际距离,求比例尺?
比例尺=图上距离÷实际距离
②已知图上距离和比例尺,求实际距离?
实际距离=图上距离÷比例尺
③已知实际距离和比例尺,求图上距离
图上距离=实际距离×比例尺
练习题
2、在比例尺是1:100的平面图上量的一间教室长7厘米,宽6厘米,这间教室占地面积是多少平方厘米?
0 10 20 30米
看着这个线段比例尺,你能理解
它的意思吗?说说看。
1、
图形的放大与缩小
1、图形的放大与缩小的特点是:形状相同,大小不同
2、图形的放大或缩小的方法:
一看,二算,三画
练习题
1、 A城到B城的实际距离是12km,画在比例尺为
1:100000的图纸上,应画多少厘米?
2、一个长5cm,宽3cm的长方形按3︰1
放大,得到的图形的周长的是多少厘米?
面积是多少平方厘米?
练习:
1 、一副地图中某两地的图上距离是5cm,
表示实际距离15km,这幅地图的比例尺是
( )。
2 、比例尺1 ︰2000000改写成线段比例尺
是( )。
D
1 ︰300000
3、在比例尺是1︰5000000的云南地图上,量得大理到楚雄的距离是3.2厘米。计算一下,大理到楚雄的实际距离大约是多少千米?
答:大理到楚雄的实际距离大约是160km。
4、在一张1:500的设计图纸上,量得一正方形建筑的边长是20cm,这个建筑物的实际占地面积是多少平方米?
(1)求边长的实际距离:
(2)求建筑物实际占地面积:
1002 = 10000(m2)
答:这个建筑物的实际占地面积是10000m2。
5、修建一个长80m、宽60m的长方形操场,用1:1000的比例尺画在图纸上,长和宽各画多少cm?
(1)求长的图上距离:
80m=8000cm
(2)求宽的图上距离:
60m=6000cm
答:长画8cm,宽画6cm。
按比例分配:
①按比例分配问题的特征是什么?
用比或者连比反映各部分占总数量的份数,或者直接给出各部分占总数量的份数。
如:一个三角形三个内角度数比是1:2:3
②按比例分配问题与平均数问题的区别是什么?
按比例分配不一定是等分,即平均分
③按比例分配问题解题方法?
(1)找出或求出要分的总数;
(2)根据已知的比求总份数;
(3)按照要分配的各部分占总数的几分之几,分别求出每一部分是多少,还可以先求出每一份,再以它为标准,分别求出各部分是多少。
练习题
1、一个三角形三个内角度数比是1:2:3,这个三角形的三个内角分别是多少?
2、做个长方体模型,共需要96米长的铁丝,这个长方体的长宽高的比是1:2:3,则这个长方体的长宽高分别是多少
该长方体的表面积是多少平方米?
体积是多少?
正比例和反比例的意义
1、成正比例的量
①两种相关联的量②一种量变化,另一种量也随着变化③比值一定
关系式:
2、成反比例的量
①两种相关联的量②一种量变化,另一种量也随着变化③积一定
关系式: x y= k (一定)
3、判断两种量成正比例还是成反比例的方法。
关键是看这两种相关联的量对应的两个数的商一定还是积一定,如果商一定就成正比例,如果积一定就成反比例。
(一定)
成正比例的量和成反比例的量有什么共同点和不同点?
正比例关系 反比例关系
相同点
变化情况
一定
关系式
变化图像
不同点
正比例关系 反比例关系
不
同
点 变化情况
一定
变化图像
比值或商
乘积
关系式
相同点
两种相关联的量,一种量随着另一种量的变化而变化。
一种量扩大(缩小),另一种量也扩大(缩小)
一种量扩大(缩小),另一种量反而缩小(扩大)
=k(一定)
X×Y=K(一定)
练习
下面各题中的两种量是不是成比例 如果成比例,成什么比例关系
(1)比例尺一定,两地的实际距离和图上距离。
(2)被除数一定,除数和商。
(3)梯形的上底和下底不变,梯形的面积和高。
(4)如果y=5x,y和x。
判断正、反比例的三个注意点
第一,注意不要被假象所迷惑。成正反比例量的特点是一个量变化,另一个量也随着变化,但仅凭此不能确定两个量是否成比例。
如:“圆的半径和面积”,表面看,圆的半径扩大或缩小,圆的面积也随着扩大或缩小,似乎成正比例,但实际上圆面积=圆半径×π ×圆半径,而π ×圆半径也是一个变量,所以圆的半径和面积不成正比例。
第二,注意不要忽略隐藏着的量。有些判断中,虽没有明确表达定量,但不能认为它一定不成比例,有可能它的定量隐含其中。
如:“订阅《中小学生报》的份数和钱数”,题中没有说出定量,但我们分析一下就可知道,钱数=份数×每份的价钱,因为订阅的是同一份报纸,它的单价是一定的,所以订阅《小学生报》的份数和钱数成正比例。
判断正、反比例的三个注意点
第三,注意不要被常量所干扰。有些判断中,可能会涉及固定的数值,也就是我们所说的常量,往往会给我们的判断增加难度,我们不能被其干扰。
如:“三角形的面积一定,它的底和高成反比例”,因为三角形的面积=底×高÷2,所以底×高=三角形面积×2,三角形的面积一定,面积的2倍也是一个定量,所以三角形面积一定,它的底和高成反比例。
怎么解正、反比例应用题:
①正、反比例应用题的特征?
②解正、反比例应用题一般方法和步骤?
练习题: 1、一台拖拉机16天耕地19.20公顷,30天可以耕地多少公顷
2、制造一批零件,计划每天做160个,15天完成。实际每天超产40个,多少天就能完成这批零件?
3、一个筑路队修一条公路,原计划每天修3.2千米,15天完成,实际每天比原计划多修了25%,实际多少天可以完成?
当堂训练
1、填空:
①一幅地图的线段比例尺是 , 它表示实际距离是图上距离的( )倍。
②)在一个比例里,两个外项的积是最小的质数,一个内项是0.5,另一个内项是( )。
③在 的图纸上,一个正方形的面积为16平方厘米,它的
实际面积是( )平方米。
④一车水果重1.8吨,按2:3:5的比例分配给甲、乙、丙三个水果店,乙水果店分得这批水果的()。
⑤把3克盐放入12克水中,盐与盐水重量的最简整数比是( )。
0
40
80
120千米
当堂训练
二、判断:
1、小麦的出粉率一定,小麦的总重量和面粉的重量成正比例关系。 ( )
2、因为甲数:乙数=25:23,所以甲数=25,乙数=23。 ( )
3、车轮的直径一定,车轮转动的周数和所行路程成正比例。 ( )
4、如果A与B成反比例,B与C也成反比例,那么A与C成正比例。 ( )
5、如果a×3=b×5,那么a:b=5:3。 ( )
6、y=8x,表示x和y成正比例。 ( )
7、半径与直径的比是1:2。 ( )
8、甲地到乙地,甲车要6小时,乙车要8小时,甲车和乙车的速度比是3:4。 ( )
当堂训练
三、选择:
1、把10克糖溶解在100克水中,糖与糖水的比是( )
A、10:1 B、1:10 C、1:11 D、11:1
2、一个圆的直径与周长的比是( )。
A、1:2 B、1: C、2:
3、一批产品,合格产品与不合格产品的比是4:1,这批产品的不合格率是( ) A、25% B、20% C、10%
4、在同一个圆里,周长与直径( )。
A、成正比例 B、成反比例C、不成比例
5、一个三角形内角度数的比是7:2:1,这个三角形( )。A、钝角三角形 B、锐角三角形 C、直角三角形
6、一条长5米的线段画在比例尺是1:100的图中,要比画在比例尺只是1:1000的图中( )。
A、长 B、短 C、一样长
7、两个圆的直径比是1:2,周长比是( )。
A、1:2 B、1:4 C、1:8
当堂训练
四、应用题:
1、一种农药水是用药和水按1:100配成的,要配制这种农药水8080千克,需要药粉多少千克?
2、做一批零件,如果每天做200个,15天可以做完,现在要在12天完成,平均每天做多少个?(比例解)
3、甲地到乙地的公路长392千米。一辆汽车3小时行了168千米。照这样计算,行完全还需要几小时?(比例解)
4、甲乙丙三种商品总价值为5800元。按数量,甲与乙的比是1:2,乙与丙的比是1:2.5;按单价,甲与乙的比是3:2,乙与丙的比是4:3。三种商品各值多少元?
5、在比例尺是1:3000000的地图上,量得两地距离是10厘米,甲乙两车同时从两地相向而行,3小时后两车相遇。已知甲乙两车的速度比是2:3,求甲乙两车的速度各是多少千米?
(6)张师傅加工一批零件,第一天完成的个数与零件的总个数的比是1:3。如果再加工15个,就可以完成这批零件的一半。这批零件共有多少个?
(7)一件工作,甲单独做要用6小时,乙单独做要用4小时。甲做完 后,两人合作,还要几小时才能做完?
(8)一个工厂由于采用新工艺,现在每件产品的成本是37.4元,比原来降低了15%。原来每件产品的成本是多少元?
(9)甲乙两列火车从相距450千米的两地同时相向开出,经过5小时正好相遇。已知甲乙两列火车的速度之比是4 :5,两列火车
每小时各行多少千米?
综合练习
1、填空:
1)一个比例有两个( )项,两个( )项。
2)判断两个比是否能组成比例,可以看它们的( )也可以用( )进行判断。
3)写出比值是2.5的比,并组成比例( )
4)在比例中,如果两个内项的分别是4和5,那么组成
两个外项的两个数的积一定是( )
内
外
5:2=10:4
20
5)甲数是乙数的1-,甲数和乙数的比是( ),比值是( )。
6)( )成= — =( )÷20=0.8=( )℅=( ):60
7)甲数和乙数的比是3:5,甲数占乙数的-,乙数占甲乙两数总数的-。
8)3x=4y,(x、y都不为0),x和 y的比是( ):( )
9)两个数的比值是4,前项和后项同时扩大3倍,比值是( )。
2
1
( )
20
2、选择
3:2
1.5
25
16
80
48
3
5
8
5
4
3
不变
8
1)两和正方形的边长的比是3:5,它们面积的比是( ),周长的比是( )。
A:1:3 B: 3:5 C:1:25 D:9:25
2)把100克白糖放如1000克水中,糖和水的比是( )
A: 1:12 B: 1:11 C: 1:10 D: 1:9
3)比的前项扩大2倍,后项缩小2倍,比值( )
A: 扩大4倍 B: 缩小4倍 C:不变 D: 扩大2倍
4)甲数的-等于乙数的- ,乙数与甲数的比是( )
A : 25:18 B: 18:25 C: 1:2 D: 2:1
5
3
6
5
D
B
C
A
A
5)一个圆柱和圆锥等高等体积,他们的底面积的比是( ) 。
A: 1:3 B: 3:1 C: 1: 9 D: 9:1
3、判断:
1)正方形的面积的比等于边长的比( )
2)如果a:b的比是3:4,3a =4b。( )
3)45分:1-时的比值是0.6。( )
4)-化简后是最简整数比是2-。( )
4
1
4
10
2
1
×
×
×
×
B
5、用21、3 、-、0.125四个数组成比值不同的比例
8
7
4、根据要求写出一个比例式
1)两个外项分别是3和x,两和内项分别是9和12。
2)等号左边的比是x:5,右边比的比值是5。
3)使各项都是整数,且两个比的比值为0.8。
