数学六年级上苏教版1.5 表面涂色的正方体课件(31张)
文档属性
| 名称 | 数学六年级上苏教版1.5 表面涂色的正方体课件(31张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-20 06:29:30 | ||
图片预览








文档简介
(共31张PPT)
第一关
(1)你会将一个正方形分割成等面积的四个小正方形吗?
试一试
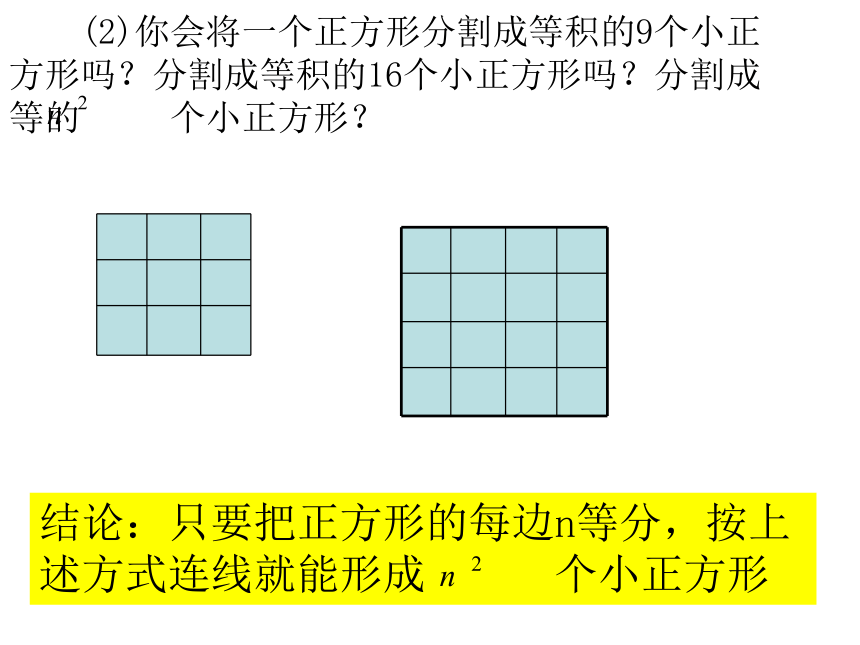
(2)你会将一个正方形分割成等积的9个小正方形吗?分割成等积的16个小正方形吗?分割成等的 个小正方形?
结论:只要把正方形的每边n等分,按上述方式连线就能形成 个小正方形
第二关
8
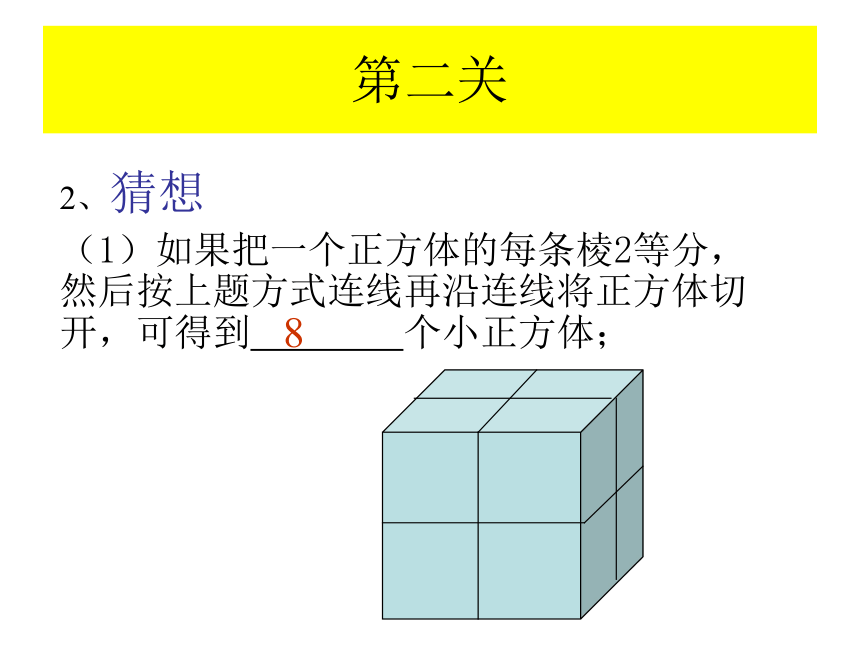
2、猜想
(1)如果把一个正方体的每条棱2等分,然后按上题方式连线再沿连线将正方体切开,可得到 个小正方体;
2、猜想
(2)将棱3等分可得 个小正方体;将棱4等分可得 个小正方体;将棱n等分可得 个小正方体.
第二关
27
64
你还记得正方体有 一些基本特征吗
填空题:
1.正方体有______个面.
2.正方体有______条棱.
3.正方体有______个顶点.
6
8
12
正方体涂色
1.小心使用工具.
2.不能损坏公物.
3.各小组要团结合作.
一个表面涂上颜色的正方体,把它的棱5等分,然后沿等分线把正方体切开,得到125个小正方体,其中3面涂色的正方体有几个?2面涂色的正方体有几个?1面涂色的正方体有几个?各面都没有涂色的正方体有几个?
你会直接回答吗?
第三关
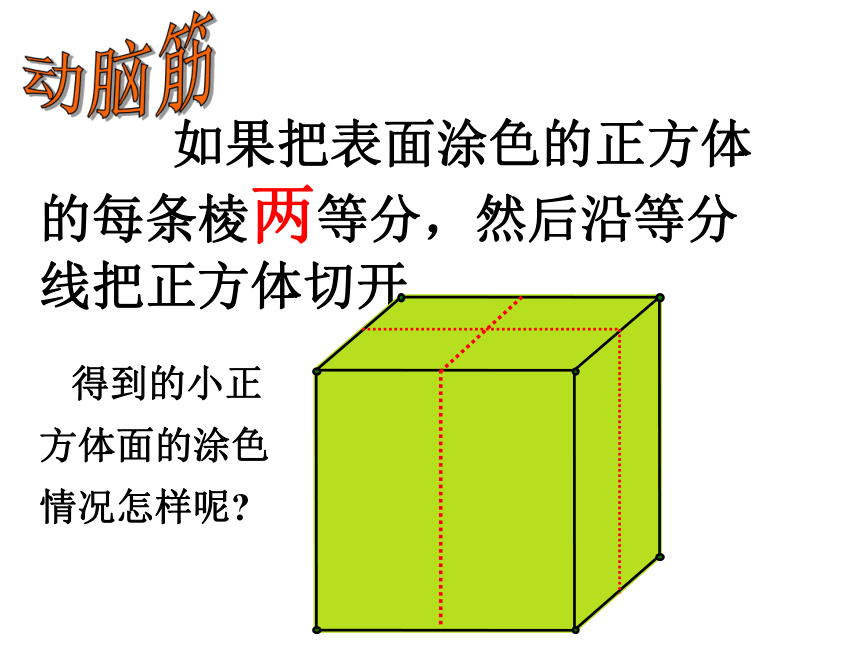
如果把表面涂色的正方体的每条棱两等分,然后沿等分线把正方体切开.
得到的小正方体面的涂色情况怎样呢
如果把表面涂色的正方体的每条棱两等分,然后沿等分线把正方体切开(如图)
得到的小正方体面的涂色情况怎样呢
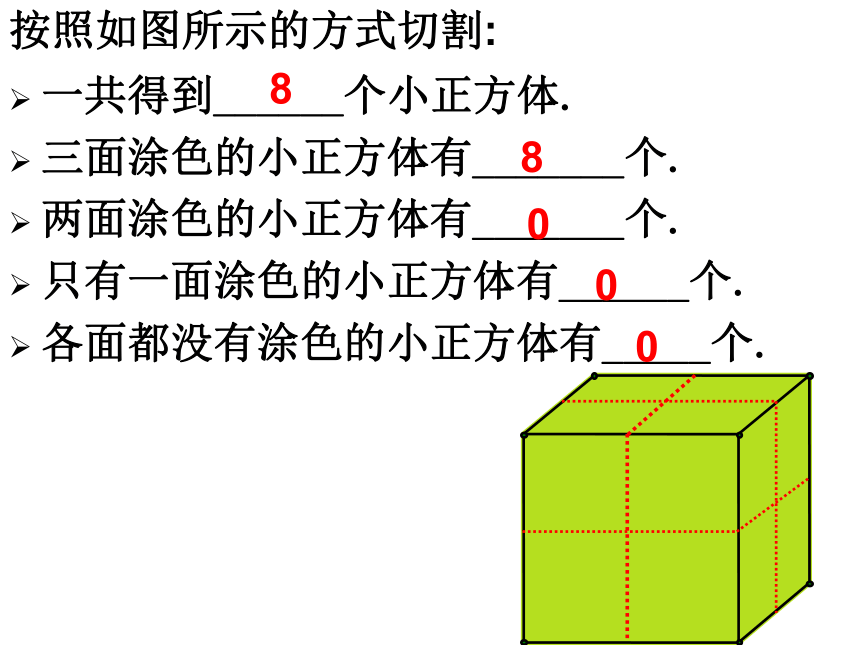
一共得到______个小正方体.
三面涂色的小正方体有_______个.
两面涂色的小正方体有_______个.
只有一面涂色的小正方体有______个.
各面都没有涂色的小正方体有_____个.
按照如图所示的方式切割:
8
8
0
0
0
想一想怎样把表面涂色的正方体的每条棱三等分,然后沿等分线把正方体切开
.
.
.
.
把表面涂色的正方体的每条棱三等分,然后沿等分线把正方体切开(如图):
就这样啦!
一共得到_____个小正方体.
三面涂色的小正方体有_____个.
两面涂色的小正方体有______个.
只有一面涂色的小正方体有_____个.
各面都没有涂色的小正方体有____个.
按照如图所示的方式切割:
27
8
12
6
1
每条棱
等分数 小正方
体总数 三面
涂色数 两面
涂色数 一面
涂色数 各面无
涂色数
2
3
小正方体表面涂色情况表
8
8
0
0
0
27
8
12
6
1
填表:
怎样把表面涂色的正方体的每条棱四等分,然后沿等分线把正方体切开
把表面涂色的正方体的每条棱四等分,然后沿等分线把正方体切开(如图) :
每条棱
等分数 小正方
体总数 三面
涂色数 两面
涂色数 一面
涂色数 各面无
涂色数
64
4
8
24
24
8
每条棱
等分数 小正方
体总数 三面
涂色数 两面
涂色数 一面
涂色数 各面无
涂色数
2 8 8 0 0 0
3 27 8 12 6 1
4
小正方体表面涂色情况表
64
8
24
24
8
一个表面涂上颜色的正方体,把它的棱5等分,然后沿等分线把正方体切开,得到125个小正方体,其中3面涂色的正方体有几个?2面涂色的正方体有几个?1面涂色的正方体有几个?各面都没有涂色的正方体有几个?
每条棱
等分数 小正方
体总数 三面
涂色数 两面
涂色数 一面
涂色数 各面无
涂色数
125
5
8
36
54
27
每条棱
等分数 小正方
体总数 三面
涂色数 两面
涂色数 一面
涂色数 各面无
涂色数
2 8 8 0 0 0
3 27 8 12 6 1
4 64 8 24 24 8
小正方体表面涂色情况表
8
36
54
27
5
n
125
8
12(n-2)
6(n-2)2
( n-2)3
n3
像这样通过对现象的观察、分析,从特殊到一般地探索这类现象规律(提出猜想)的思想方法称为归纳。当然这种猜想有时是正确的,有时是错误的。
归纳
长方体和正方体有哪些不同点
把长、宽、高分别为m、n、p(均大于2)个单位长度的表面涂色的正方体切割成边长为1的小正方体,如何计算小正方体的总数、涂色面数不同的小正方体个数呢?
m
n
p
每条棱
等分数 三面
涂色数 两面
涂色数 一面
涂色数 各面无
涂色数
小正方体表面涂色情况表
n
8
12(n-2)
6(n-2)2
当n=10时,三面涂色的小正方体有____个.
两面涂色的小正方体有____个.
一面涂色的小正方体有____个.
各面无涂色的小正方体有____个.
8
96
384
512
( n-2)3
一共得到______个小正方体.
三面涂色的小正方体有_______个.
两面涂色的小正方体有_______个.
只有一面涂色的小正方体有______个.
各面都没有涂色的小正方体有_____个.
按照如图所示的方式切割:
第一关
(1)你会将一个正方形分割成等面积的四个小正方形吗?
试一试
(2)你会将一个正方形分割成等积的9个小正方形吗?分割成等积的16个小正方形吗?分割成等的 个小正方形?
结论:只要把正方形的每边n等分,按上述方式连线就能形成 个小正方形
第二关
8
2、猜想
(1)如果把一个正方体的每条棱2等分,然后按上题方式连线再沿连线将正方体切开,可得到 个小正方体;
2、猜想
(2)将棱3等分可得 个小正方体;将棱4等分可得 个小正方体;将棱n等分可得 个小正方体.
第二关
27
64
你还记得正方体有 一些基本特征吗
填空题:
1.正方体有______个面.
2.正方体有______条棱.
3.正方体有______个顶点.
6
8
12
正方体涂色
1.小心使用工具.
2.不能损坏公物.
3.各小组要团结合作.
一个表面涂上颜色的正方体,把它的棱5等分,然后沿等分线把正方体切开,得到125个小正方体,其中3面涂色的正方体有几个?2面涂色的正方体有几个?1面涂色的正方体有几个?各面都没有涂色的正方体有几个?
你会直接回答吗?
第三关
如果把表面涂色的正方体的每条棱两等分,然后沿等分线把正方体切开.
得到的小正方体面的涂色情况怎样呢
如果把表面涂色的正方体的每条棱两等分,然后沿等分线把正方体切开(如图)
得到的小正方体面的涂色情况怎样呢
一共得到______个小正方体.
三面涂色的小正方体有_______个.
两面涂色的小正方体有_______个.
只有一面涂色的小正方体有______个.
各面都没有涂色的小正方体有_____个.
按照如图所示的方式切割:
8
8
0
0
0
想一想怎样把表面涂色的正方体的每条棱三等分,然后沿等分线把正方体切开
.
.
.
.
把表面涂色的正方体的每条棱三等分,然后沿等分线把正方体切开(如图):
就这样啦!
一共得到_____个小正方体.
三面涂色的小正方体有_____个.
两面涂色的小正方体有______个.
只有一面涂色的小正方体有_____个.
各面都没有涂色的小正方体有____个.
按照如图所示的方式切割:
27
8
12
6
1
每条棱
等分数 小正方
体总数 三面
涂色数 两面
涂色数 一面
涂色数 各面无
涂色数
2
3
小正方体表面涂色情况表
8
8
0
0
0
27
8
12
6
1
填表:
怎样把表面涂色的正方体的每条棱四等分,然后沿等分线把正方体切开
把表面涂色的正方体的每条棱四等分,然后沿等分线把正方体切开(如图) :
每条棱
等分数 小正方
体总数 三面
涂色数 两面
涂色数 一面
涂色数 各面无
涂色数
64
4
8
24
24
8
每条棱
等分数 小正方
体总数 三面
涂色数 两面
涂色数 一面
涂色数 各面无
涂色数
2 8 8 0 0 0
3 27 8 12 6 1
4
小正方体表面涂色情况表
64
8
24
24
8
一个表面涂上颜色的正方体,把它的棱5等分,然后沿等分线把正方体切开,得到125个小正方体,其中3面涂色的正方体有几个?2面涂色的正方体有几个?1面涂色的正方体有几个?各面都没有涂色的正方体有几个?
每条棱
等分数 小正方
体总数 三面
涂色数 两面
涂色数 一面
涂色数 各面无
涂色数
125
5
8
36
54
27
每条棱
等分数 小正方
体总数 三面
涂色数 两面
涂色数 一面
涂色数 各面无
涂色数
2 8 8 0 0 0
3 27 8 12 6 1
4 64 8 24 24 8
小正方体表面涂色情况表
8
36
54
27
5
n
125
8
12(n-2)
6(n-2)2
( n-2)3
n3
像这样通过对现象的观察、分析,从特殊到一般地探索这类现象规律(提出猜想)的思想方法称为归纳。当然这种猜想有时是正确的,有时是错误的。
归纳
长方体和正方体有哪些不同点
把长、宽、高分别为m、n、p(均大于2)个单位长度的表面涂色的正方体切割成边长为1的小正方体,如何计算小正方体的总数、涂色面数不同的小正方体个数呢?
m
n
p
每条棱
等分数 三面
涂色数 两面
涂色数 一面
涂色数 各面无
涂色数
小正方体表面涂色情况表
n
8
12(n-2)
6(n-2)2
当n=10时,三面涂色的小正方体有____个.
两面涂色的小正方体有____个.
一面涂色的小正方体有____个.
各面无涂色的小正方体有____个.
8
96
384
512
( n-2)3
一共得到______个小正方体.
三面涂色的小正方体有_______个.
两面涂色的小正方体有_______个.
只有一面涂色的小正方体有______个.
各面都没有涂色的小正方体有_____个.
按照如图所示的方式切割:
