备战2018中考数学专题突破 第八讲方程(组)与不等式(组)
文档属性
| 名称 | 备战2018中考数学专题突破 第八讲方程(组)与不等式(组) |
|
|
| 格式 | zip | ||
| 文件大小 | 292.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-21 00:00:00 | ||
图片预览





文档简介
第八讲方程(组)与不等式(组)
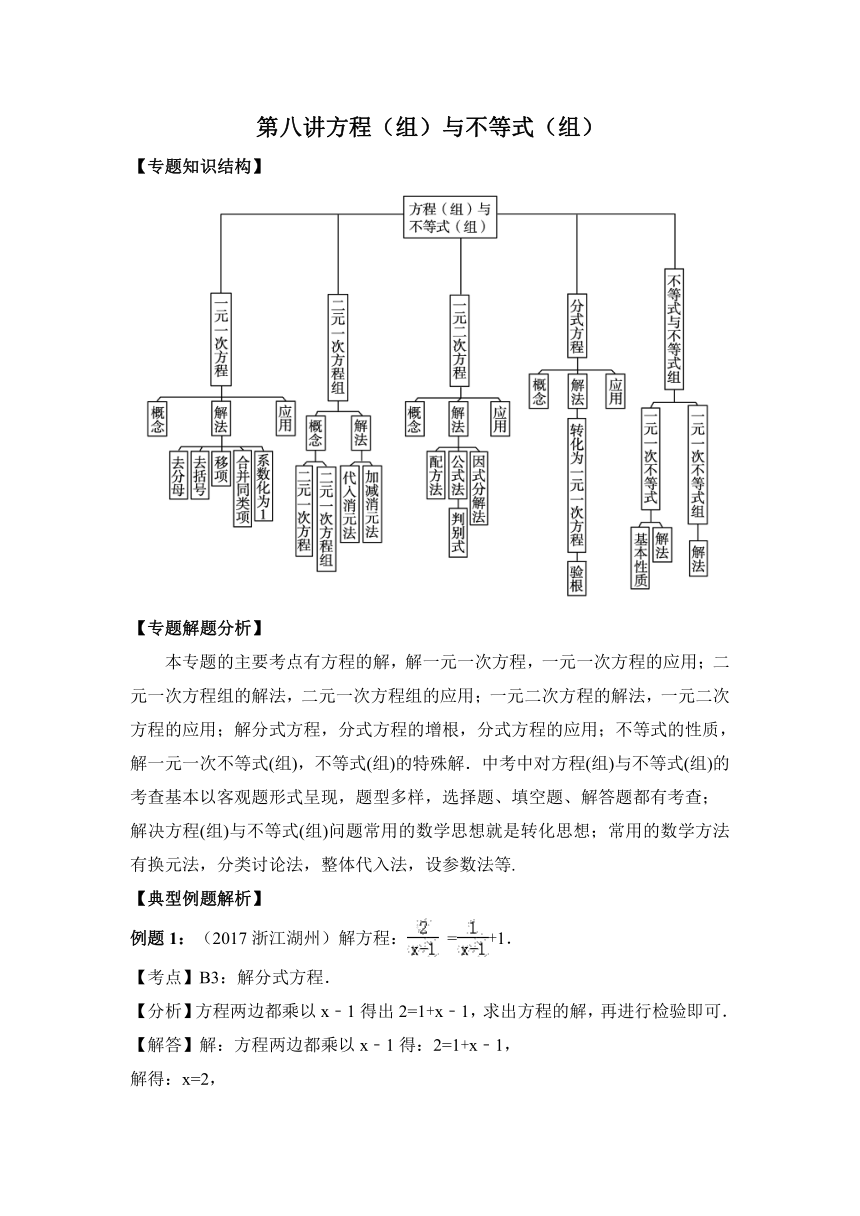
【专题知识结构】
【专题解题分析】
本专题的主要考点有方程的解,解一元一次方程,一元一次方程的应用;二元一次方程组的解法,二元一次方程组的应用;一元二次方程的解法,一元二次方程的应用;解分式方程,分式方程的增根,分式方程的应用;不等式的性质,解一元一次不等式(组),不等式(组)的特殊解.中考中对方程(组)与不等式(组)的考查基本以客观题形式呈现,题型多样,选择题、填空题、解答题都有考查;
解决方程(组)与不等式(组)问题常用的数学思想就是转化思想;常用的数学方法有换元法,分类讨论法,整体代入法,设参数法等.
【典型例题解析】
例题1:(2017浙江湖州)解方程:
=+1.
【考点】B3:解分式方程.
【分析】方程两边都乘以x﹣1得出2=1+x﹣1,求出方程的解,再进行检验即可.
【解答】解:方程两边都乘以x﹣1得:2=1+x﹣1,
解得:x=2,
检验:∵当x=2时,x﹣1≠0,
∴x=2是原方程的解,
即原方程的解为x=2.
例题2:(2017广东)学校团委组织志愿者到图书馆整理一批新进的图书.若男生每人整理30本,女生每人整理20本,共能整理680本;若男生每人整理50本,女生每人整理40本,共能整理1240本.求男生、女生志愿者各有多少人?
【考点】9A:二元一次方程组的应用.
【分析】设男生志愿者有x人,女生志愿者有y人,根据“若男生每人整理30本,女生每人整理20本,共能整理680本;若男生每人整理50本,女生每人整理40本,共能整理1240本”,即可得出关于x、y的二元一次方程组,解之即可得出结论.
【解答】解:设男生志愿者有x人,女生志愿者有y人,
根据题意得:,
解得:.
答:男生志愿者有12人,女生志愿者有16人.
例题3:(2017浙江湖州)对于任意实数a,b,定义关于“ ”的一种运算如下:a b=2a﹣b.例如:5 2=2×5﹣2=8,(﹣3) 4=2×(﹣3)﹣4=﹣10.
(1)若3 x=﹣2011,求x的值;
(2)若x 3<5,求x的取值范围.
【考点】C6:解一元一次不等式;2C:实数的运算;86:解一元一次方程.
【分析】(1)根据新定义列出关于x的方程,解之可得;
(2)根据新定义列出关于x的一元一次不等式,解之可得.
【解答】解:(1)根据题意,得:2×3﹣x=﹣2011,
解得:x=2017;
(2)根据题意,得:2x﹣3<5,
解得:x<4.
例题4:.(2017四川眉山)东坡某烘焙店生产的蛋糕礼盒分为六个档次,第一档次(即最低档次)的产品每天生产76件,每件利润10元.调查表明:生产提高一个档次的蛋糕产品,该产品每件利润增加2元.
(1)若生产的某批次蛋糕每件利润为14元,此批次蛋糕属第几档次产品;
(2)由于生产工序不同,蛋糕产品每提高一个档次,一天产量会减少4件.若生产的某档次产品一天的总利润为1080元,该烘焙店生产的是第几档次的产品?
【考点】AD:一元二次方程的应用.
【分析】(1)根据生产提高一个档次的蛋糕产品,该产品每件利润增加2元,即可求出每件利润为14元的蛋糕属第几档次产品;
(2)设烘焙店生产的是第x档次的产品,根据单件利润×销售数量=总利润,即可得出关于x的一元二次方程,解之即可得出结论.
【解答】解:(1)(14﹣10)÷2+1=3(档次).
答:此批次蛋糕属第3档次产品.
(2)设烘焙店生产的是第x档次的产品,
根据题意得:(2x+8)×(76+4﹣4x)=1080,
整理得:x2﹣16x+55=0,
解得:x1=5,x2=11.
答:该烘焙店生产的是第5档次或第11档次的产品.
例题5:(2017四川南充)学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
【考点】C9:一元一次不等式的应用;9A:二元一次方程组的应用.
【分析】(1)可设1辆甲种客车的租金是x元,1辆乙种客车的租金是y元,根据等量关系:①1辆甲种客车和3辆乙种客车共需租金1240元,②3辆甲种客车和2辆乙种客车共需租金1760元,列出方程组求解即可;
(2)由于求最节省的租车费用,可知租用甲种客车6辆,租用乙客车2辆,进而求解即可.
【解答】解:(1)设1辆甲种客车的租金是x元,1辆乙种客车的租金是y元,依题意有
,
解得.
故1辆甲种客车的租金是400元,1辆乙种客车的租金是280元;
(2)租用甲种客车6辆,租用乙客车2辆是最节省的租车费用,
400×6+280×2
=2400+560
=2960(元).
答:最节省的租车费用是2960元.
例题6:(2017年贵州省安顺)某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
【考点】B7:分式方程的应用;CE:一元一次不等式组的应用.
【分析】(1)设甲种玩具进价x元/件,则乙种玩具进价为(40﹣x)元/件,根据已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同可列方程求解.
(2)设购进甲种玩具y件,则购进乙种玩具(48﹣y)件,根据甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,可列出不等式组求解.
【解答】解:设甲种玩具进价x元/件,则乙种玩具进价为(40﹣x)元/件,
=
x=15,
经检验x=15是原方程的解.
∴40﹣x=25.
甲,乙两种玩具分别是15元/件,25元/件;
(2)设购进甲种玩具y件,则购进乙种玩具(48﹣y)件,
,
解得20≤y<24.
因为y是整数,甲种玩具的件数少于乙种玩具的件数,
∴y取20,21,22,23,
共有4种方案.
【达标检测评估】
选择题:
1.
(2017年贵州省安顺)若关于x的方程x2+mx+1=0有两个不相等的实数根,则m的值可以是( )
A.0
B.﹣1
C.2
D.﹣3
【考点】AA:根的判别式.
【分析】首先根据题意求得判别式△=m2﹣4>0,然后根据△>0 方程有两个不相等的实数根;求得答案.
【解答】解:∵a=1,b=m,c=1,
∴△=b2﹣4ac=m2﹣4×1×1=m2﹣4,
∵关于x的方程x2+mx+1=0有两个不相等的实数根,
∴m2﹣4>0,
则m的值可以是:﹣3,
故选:D.
2.
(2017广东)如果2是方程x2﹣3x+k=0的一个根,则常数k的值为( )
A.1
B.2
C.﹣1
D.﹣2
【考点】A3:一元二次方程的解.
【分析】把x=2代入已知方程列出关于k的新方程,通过解方程来求k的值.
【解答】解:∵2是一元二次方程x2﹣3x+k=0的一个根,
∴22﹣3×2+k=0,
解得,k=2.
故选:B.
3.
(2017浙江湖州)一元一次不等式组的解是( )
A.x>﹣1
B.x≤2
C.﹣1<x≤2
D.x>﹣1或x≤2
【考点】CB:解一元一次不等式组.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:解不等式2x>x﹣1,得:x>﹣1,
解不等式x≤1,得:x≤2,
则不等式组的解集为﹣1<x≤2,
故选:C.
4.
(2017贵州黔东南)已知一元二次方程x2﹣2x﹣1=0的两根分别为x1,x2,则+的值为( )
A.2
B.﹣1
C.
D.﹣2
【考点】AB:根与系数的关系.
【分析】根据根与系数的关系得到x1+x2=2,x1x2=﹣1,利用通分得到+=,然后利用整体代入的方法计算
【解答】解:根据题意得x1+x2=2,x1x2=﹣1,
所以+===﹣2.
故选D.
填空题:
5.
(2017四川南充)如果=1,那么m= 2 .
【考点】B3:解分式方程.
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到m的值,经检验即可得到分式方程的解.
【解答】解:去分母得:1=m﹣1,
解得:m=2,
经检验m=2是分式方程的解,
故答案为:2
6.
(2016·辽宁丹东·3分)某公司今年4月份营业额为60万元,6月份营业额达到100万元,设该公司5、6两个月营业额的月均增长率为x,则可列方程为 60(1+x)2=100 .
【考点】由实际问题抽象出一元二次方程.
【分析】设平均每月的增长率为x,根据4月份的营业额为60万元,6月份的营业额为100万元,分别表示出5,6月的营业额,即可列出方程.
【解答】解:设平均每月的增长率为x,
根据题意可得:60(1+x)2=100.
故答案为:60(1+x)2=100.
7.
(2016·湖北黄石·3分)关于x的一元二次方程x2+2x﹣2m+1=0的两实数根之积为负,则实数m的取值范围是 m> .
【分析】设x1、x2为方程x2+2x﹣2m+1=0的两个实数根.由方程有实数根以及两根之积为负可得出关于m的一元一次不等式组,解不等式组即可得出结论.
【解答】解:设x1、x2为方程x2+2x﹣2m+1=0的两个实数根,
由已知得:,即
解得:m>.
故答案为:m>.
【点评】本题考查了根与系数的关系、根的判别式以及解一元一次不等式,解题的关键是得出关于m的一元一次不等式组.本题属于基础题,难度不大,解决该题型题目时,根据根的情况结合根的判别式以及根与系数的关系得出关于m的一元一次不等式组是关键.
8.
(2016·四川宜宾)今年“五一”节,A、B两人到商场购物,A购3件甲商品和2件乙商品共支付16元,B购5件甲商品和3件乙商品共支付25元,求一件甲商品和一件乙商品各售多少元.设甲商品售价x元/件,乙商品售价y元/件,则可列出方程组 .
【考点】由实际问题抽象出二元一次方程组.
【分析】分别利用“A购3件甲商品和2件乙商品共支付16元,B购5件甲商品和3件乙商品共支付25元”得出等式求出答案.
【解答】解:设甲商品售价x元/件,乙商品售价y元/件,则可列出方程组:
.
故答案为:.
解答题:
9.
(2017湖南怀化)解不等式组,并把它的解集在数轴上表示出来.
【考点】CB:解一元一次不等式组;C4:在数轴上表示不等式的解集.
【分析】首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
【解答】解:解不等式①,得x<3.
解不等式②,得x≥﹣1.
所以,不等式组的解集是﹣1≤x<3.
它的解集在数轴上表示出来为:
10.
(2017湖南怀化)为加强中小学生安全教育,某校组织了“防溺水”知识竞赛,对表现优异的班级进行奖励,学校购买了若干副乒乓球拍和羽毛球拍,购买2副乒乓球拍和1副羽毛球拍共需116元;购买3副乒乓球拍和2副羽毛球拍共需204元.
(1)求购买1副乒乓球拍和1副羽毛球拍各需多少元;
(2)若学校购买乒乓球拍和羽毛球拍共30幅,且支出不超过1480元,则最多能够购买多少副羽毛球拍?
【考点】C9:一元一次不等式的应用;9A:二元一次方程组的应用.
【分析】(1)设购买一副乒乓球拍x元,一副羽毛球拍y元,由购买2副乒乓球拍和1副羽毛球拍共需116元,购买3副乒乓球拍和2副羽毛球拍共需204元,可得出方程组,解出即可.
(2)设可购买a副羽毛球拍,则购买乒乓球拍(30﹣a)副,根据购买足球和篮球的总费用不超过1480元建立不等式,求出其解即可.
【解答】解:(1)设购买一副乒乓球拍x元,一副羽毛球拍y元,
由题意得,,
解得:.
答:购买一副乒乓球拍28元,一副羽毛球拍60元.
(2)设可购买a副羽毛球拍,则购买乒乓球拍(30﹣a)副,
由题意得,60a+28(30﹣a)≤1480,
解得:a≤20,
答:这所中学最多可购买20副羽毛球拍.
11.
(2017四川南充)已知关于x的一元二次方程x2﹣(m﹣3)x﹣m=0
(1)求证:方程有两个不相等的实数根;
(2)如果方程的两实根为x1、x2,且x12+x22﹣x1x2=7,求m的值.
【考点】AB:根与系数的关系;AA:根的判别式.
【分析】(1)要证明方程有两个不相等的实数根,只要证明原来的一元二次方程的△的值大于0即可;
(2)根据根与系数的关系可以得到关于m的方程,从而可以求得m的值.
【解答】(1)证明:∵x2﹣(m﹣3)x﹣m=0,
∴△=[﹣(m﹣3)]2﹣4×1×(﹣m)=m2﹣2m+9=(m﹣1)2+8>0,
∴方程有两个不相等的实数根;
(2)∵x2﹣(m﹣3)x﹣m=0,方程的两实根为x1、x2,且x12+x22﹣x1x2=7,
∴,
∴(m﹣3)2﹣3×(﹣m)=7,
解得,m1=1,m2=2,
即m的值是1或2.
12.
(2017山东日照)某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
【考点】B7:分式方程的应用;C9:一元一次不等式的应用.
【分析】(1)设原计划每年绿化面积为x万平方米,则实际每年绿化面积为1.6x万平方米.根据“实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务”列出方程;
(2)设平均每年绿化面积增加a万平方米.则由“完成新增绿化面积不超过2年”列出不等式.
【解答】解:(1)设原计划每年绿化面积为x万平方米,则实际每年绿化面积为1.6x万平方米,根据题意,得
﹣=4
解得:x=33.75,
经检验x=33.75是原分式方程的解,
则1.6x=1.6×33.75=54(万平方米).
答:实际每年绿化面积为54万平方米;
(2)设平均每年绿化面积增加a万平方米,根据题意得
54×2+2(54+a)≥360
解得:a≥72.
答:则至少每年平均增加72万平方米.
【专题知识结构】
【专题解题分析】
本专题的主要考点有方程的解,解一元一次方程,一元一次方程的应用;二元一次方程组的解法,二元一次方程组的应用;一元二次方程的解法,一元二次方程的应用;解分式方程,分式方程的增根,分式方程的应用;不等式的性质,解一元一次不等式(组),不等式(组)的特殊解.中考中对方程(组)与不等式(组)的考查基本以客观题形式呈现,题型多样,选择题、填空题、解答题都有考查;
解决方程(组)与不等式(组)问题常用的数学思想就是转化思想;常用的数学方法有换元法,分类讨论法,整体代入法,设参数法等.
【典型例题解析】
例题1:(2017浙江湖州)解方程:
=+1.
【考点】B3:解分式方程.
【分析】方程两边都乘以x﹣1得出2=1+x﹣1,求出方程的解,再进行检验即可.
【解答】解:方程两边都乘以x﹣1得:2=1+x﹣1,
解得:x=2,
检验:∵当x=2时,x﹣1≠0,
∴x=2是原方程的解,
即原方程的解为x=2.
例题2:(2017广东)学校团委组织志愿者到图书馆整理一批新进的图书.若男生每人整理30本,女生每人整理20本,共能整理680本;若男生每人整理50本,女生每人整理40本,共能整理1240本.求男生、女生志愿者各有多少人?
【考点】9A:二元一次方程组的应用.
【分析】设男生志愿者有x人,女生志愿者有y人,根据“若男生每人整理30本,女生每人整理20本,共能整理680本;若男生每人整理50本,女生每人整理40本,共能整理1240本”,即可得出关于x、y的二元一次方程组,解之即可得出结论.
【解答】解:设男生志愿者有x人,女生志愿者有y人,
根据题意得:,
解得:.
答:男生志愿者有12人,女生志愿者有16人.
例题3:(2017浙江湖州)对于任意实数a,b,定义关于“ ”的一种运算如下:a b=2a﹣b.例如:5 2=2×5﹣2=8,(﹣3) 4=2×(﹣3)﹣4=﹣10.
(1)若3 x=﹣2011,求x的值;
(2)若x 3<5,求x的取值范围.
【考点】C6:解一元一次不等式;2C:实数的运算;86:解一元一次方程.
【分析】(1)根据新定义列出关于x的方程,解之可得;
(2)根据新定义列出关于x的一元一次不等式,解之可得.
【解答】解:(1)根据题意,得:2×3﹣x=﹣2011,
解得:x=2017;
(2)根据题意,得:2x﹣3<5,
解得:x<4.
例题4:.(2017四川眉山)东坡某烘焙店生产的蛋糕礼盒分为六个档次,第一档次(即最低档次)的产品每天生产76件,每件利润10元.调查表明:生产提高一个档次的蛋糕产品,该产品每件利润增加2元.
(1)若生产的某批次蛋糕每件利润为14元,此批次蛋糕属第几档次产品;
(2)由于生产工序不同,蛋糕产品每提高一个档次,一天产量会减少4件.若生产的某档次产品一天的总利润为1080元,该烘焙店生产的是第几档次的产品?
【考点】AD:一元二次方程的应用.
【分析】(1)根据生产提高一个档次的蛋糕产品,该产品每件利润增加2元,即可求出每件利润为14元的蛋糕属第几档次产品;
(2)设烘焙店生产的是第x档次的产品,根据单件利润×销售数量=总利润,即可得出关于x的一元二次方程,解之即可得出结论.
【解答】解:(1)(14﹣10)÷2+1=3(档次).
答:此批次蛋糕属第3档次产品.
(2)设烘焙店生产的是第x档次的产品,
根据题意得:(2x+8)×(76+4﹣4x)=1080,
整理得:x2﹣16x+55=0,
解得:x1=5,x2=11.
答:该烘焙店生产的是第5档次或第11档次的产品.
例题5:(2017四川南充)学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
【考点】C9:一元一次不等式的应用;9A:二元一次方程组的应用.
【分析】(1)可设1辆甲种客车的租金是x元,1辆乙种客车的租金是y元,根据等量关系:①1辆甲种客车和3辆乙种客车共需租金1240元,②3辆甲种客车和2辆乙种客车共需租金1760元,列出方程组求解即可;
(2)由于求最节省的租车费用,可知租用甲种客车6辆,租用乙客车2辆,进而求解即可.
【解答】解:(1)设1辆甲种客车的租金是x元,1辆乙种客车的租金是y元,依题意有
,
解得.
故1辆甲种客车的租金是400元,1辆乙种客车的租金是280元;
(2)租用甲种客车6辆,租用乙客车2辆是最节省的租车费用,
400×6+280×2
=2400+560
=2960(元).
答:最节省的租车费用是2960元.
例题6:(2017年贵州省安顺)某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
【考点】B7:分式方程的应用;CE:一元一次不等式组的应用.
【分析】(1)设甲种玩具进价x元/件,则乙种玩具进价为(40﹣x)元/件,根据已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同可列方程求解.
(2)设购进甲种玩具y件,则购进乙种玩具(48﹣y)件,根据甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,可列出不等式组求解.
【解答】解:设甲种玩具进价x元/件,则乙种玩具进价为(40﹣x)元/件,
=
x=15,
经检验x=15是原方程的解.
∴40﹣x=25.
甲,乙两种玩具分别是15元/件,25元/件;
(2)设购进甲种玩具y件,则购进乙种玩具(48﹣y)件,
,
解得20≤y<24.
因为y是整数,甲种玩具的件数少于乙种玩具的件数,
∴y取20,21,22,23,
共有4种方案.
【达标检测评估】
选择题:
1.
(2017年贵州省安顺)若关于x的方程x2+mx+1=0有两个不相等的实数根,则m的值可以是( )
A.0
B.﹣1
C.2
D.﹣3
【考点】AA:根的判别式.
【分析】首先根据题意求得判别式△=m2﹣4>0,然后根据△>0 方程有两个不相等的实数根;求得答案.
【解答】解:∵a=1,b=m,c=1,
∴△=b2﹣4ac=m2﹣4×1×1=m2﹣4,
∵关于x的方程x2+mx+1=0有两个不相等的实数根,
∴m2﹣4>0,
则m的值可以是:﹣3,
故选:D.
2.
(2017广东)如果2是方程x2﹣3x+k=0的一个根,则常数k的值为( )
A.1
B.2
C.﹣1
D.﹣2
【考点】A3:一元二次方程的解.
【分析】把x=2代入已知方程列出关于k的新方程,通过解方程来求k的值.
【解答】解:∵2是一元二次方程x2﹣3x+k=0的一个根,
∴22﹣3×2+k=0,
解得,k=2.
故选:B.
3.
(2017浙江湖州)一元一次不等式组的解是( )
A.x>﹣1
B.x≤2
C.﹣1<x≤2
D.x>﹣1或x≤2
【考点】CB:解一元一次不等式组.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:解不等式2x>x﹣1,得:x>﹣1,
解不等式x≤1,得:x≤2,
则不等式组的解集为﹣1<x≤2,
故选:C.
4.
(2017贵州黔东南)已知一元二次方程x2﹣2x﹣1=0的两根分别为x1,x2,则+的值为( )
A.2
B.﹣1
C.
D.﹣2
【考点】AB:根与系数的关系.
【分析】根据根与系数的关系得到x1+x2=2,x1x2=﹣1,利用通分得到+=,然后利用整体代入的方法计算
【解答】解:根据题意得x1+x2=2,x1x2=﹣1,
所以+===﹣2.
故选D.
填空题:
5.
(2017四川南充)如果=1,那么m= 2 .
【考点】B3:解分式方程.
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到m的值,经检验即可得到分式方程的解.
【解答】解:去分母得:1=m﹣1,
解得:m=2,
经检验m=2是分式方程的解,
故答案为:2
6.
(2016·辽宁丹东·3分)某公司今年4月份营业额为60万元,6月份营业额达到100万元,设该公司5、6两个月营业额的月均增长率为x,则可列方程为 60(1+x)2=100 .
【考点】由实际问题抽象出一元二次方程.
【分析】设平均每月的增长率为x,根据4月份的营业额为60万元,6月份的营业额为100万元,分别表示出5,6月的营业额,即可列出方程.
【解答】解:设平均每月的增长率为x,
根据题意可得:60(1+x)2=100.
故答案为:60(1+x)2=100.
7.
(2016·湖北黄石·3分)关于x的一元二次方程x2+2x﹣2m+1=0的两实数根之积为负,则实数m的取值范围是 m> .
【分析】设x1、x2为方程x2+2x﹣2m+1=0的两个实数根.由方程有实数根以及两根之积为负可得出关于m的一元一次不等式组,解不等式组即可得出结论.
【解答】解:设x1、x2为方程x2+2x﹣2m+1=0的两个实数根,
由已知得:,即
解得:m>.
故答案为:m>.
【点评】本题考查了根与系数的关系、根的判别式以及解一元一次不等式,解题的关键是得出关于m的一元一次不等式组.本题属于基础题,难度不大,解决该题型题目时,根据根的情况结合根的判别式以及根与系数的关系得出关于m的一元一次不等式组是关键.
8.
(2016·四川宜宾)今年“五一”节,A、B两人到商场购物,A购3件甲商品和2件乙商品共支付16元,B购5件甲商品和3件乙商品共支付25元,求一件甲商品和一件乙商品各售多少元.设甲商品售价x元/件,乙商品售价y元/件,则可列出方程组 .
【考点】由实际问题抽象出二元一次方程组.
【分析】分别利用“A购3件甲商品和2件乙商品共支付16元,B购5件甲商品和3件乙商品共支付25元”得出等式求出答案.
【解答】解:设甲商品售价x元/件,乙商品售价y元/件,则可列出方程组:
.
故答案为:.
解答题:
9.
(2017湖南怀化)解不等式组,并把它的解集在数轴上表示出来.
【考点】CB:解一元一次不等式组;C4:在数轴上表示不等式的解集.
【分析】首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
【解答】解:解不等式①,得x<3.
解不等式②,得x≥﹣1.
所以,不等式组的解集是﹣1≤x<3.
它的解集在数轴上表示出来为:
10.
(2017湖南怀化)为加强中小学生安全教育,某校组织了“防溺水”知识竞赛,对表现优异的班级进行奖励,学校购买了若干副乒乓球拍和羽毛球拍,购买2副乒乓球拍和1副羽毛球拍共需116元;购买3副乒乓球拍和2副羽毛球拍共需204元.
(1)求购买1副乒乓球拍和1副羽毛球拍各需多少元;
(2)若学校购买乒乓球拍和羽毛球拍共30幅,且支出不超过1480元,则最多能够购买多少副羽毛球拍?
【考点】C9:一元一次不等式的应用;9A:二元一次方程组的应用.
【分析】(1)设购买一副乒乓球拍x元,一副羽毛球拍y元,由购买2副乒乓球拍和1副羽毛球拍共需116元,购买3副乒乓球拍和2副羽毛球拍共需204元,可得出方程组,解出即可.
(2)设可购买a副羽毛球拍,则购买乒乓球拍(30﹣a)副,根据购买足球和篮球的总费用不超过1480元建立不等式,求出其解即可.
【解答】解:(1)设购买一副乒乓球拍x元,一副羽毛球拍y元,
由题意得,,
解得:.
答:购买一副乒乓球拍28元,一副羽毛球拍60元.
(2)设可购买a副羽毛球拍,则购买乒乓球拍(30﹣a)副,
由题意得,60a+28(30﹣a)≤1480,
解得:a≤20,
答:这所中学最多可购买20副羽毛球拍.
11.
(2017四川南充)已知关于x的一元二次方程x2﹣(m﹣3)x﹣m=0
(1)求证:方程有两个不相等的实数根;
(2)如果方程的两实根为x1、x2,且x12+x22﹣x1x2=7,求m的值.
【考点】AB:根与系数的关系;AA:根的判别式.
【分析】(1)要证明方程有两个不相等的实数根,只要证明原来的一元二次方程的△的值大于0即可;
(2)根据根与系数的关系可以得到关于m的方程,从而可以求得m的值.
【解答】(1)证明:∵x2﹣(m﹣3)x﹣m=0,
∴△=[﹣(m﹣3)]2﹣4×1×(﹣m)=m2﹣2m+9=(m﹣1)2+8>0,
∴方程有两个不相等的实数根;
(2)∵x2﹣(m﹣3)x﹣m=0,方程的两实根为x1、x2,且x12+x22﹣x1x2=7,
∴,
∴(m﹣3)2﹣3×(﹣m)=7,
解得,m1=1,m2=2,
即m的值是1或2.
12.
(2017山东日照)某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
【考点】B7:分式方程的应用;C9:一元一次不等式的应用.
【分析】(1)设原计划每年绿化面积为x万平方米,则实际每年绿化面积为1.6x万平方米.根据“实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务”列出方程;
(2)设平均每年绿化面积增加a万平方米.则由“完成新增绿化面积不超过2年”列出不等式.
【解答】解:(1)设原计划每年绿化面积为x万平方米,则实际每年绿化面积为1.6x万平方米,根据题意,得
﹣=4
解得:x=33.75,
经检验x=33.75是原分式方程的解,
则1.6x=1.6×33.75=54(万平方米).
答:实际每年绿化面积为54万平方米;
(2)设平均每年绿化面积增加a万平方米,根据题意得
54×2+2(54+a)≥360
解得:a≥72.
答:则至少每年平均增加72万平方米.
同课章节目录
