备战2018中考数学专题突破 第二讲统计与概率
文档属性
| 名称 | 备战2018中考数学专题突破 第二讲统计与概率 |  | |
| 格式 | zip | ||
| 文件大小 | 409.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-21 14:45:36 | ||
图片预览



文档简介
第二讲统计与概率
【专题知识结构】
【专题解题分析】
统计与概率在中考中的常考点有数据的收集方法,平均数、众数和中位数的计算与选择,方差和标准差的计算和应用,统计图的应用及信息综合分析;事件的分类,简单事件的概率计算,画树状图或列表求概率,对频率和概率的理解等.统计与概率在中考中一般以客观题的形式进行考查,选择题、填空题较多,同时考查多个考点的综合性题目一般以解答题的形式进行考查;
解决统计与概率问题常用的数学思想是方程思想和分类讨论思想;常用的数学方法有分类讨论法,整体代入法等.
【典型例题解析】
例题1:
如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A.16,10.5
B.8,9
C.16,8.5
D.8,8.5
【考点】W5:众数;VC:条形统计图;W4:中位数.
【分析】根据中位数、众数的概念分别求得这组数据的中位数、众数,由图可知锻炼时间超过8小时的有14+7=21人.
【解答】解:众数是一组数据中出现次数最多的数,即8;
而将这组数据从小到大的顺序排列后,处于中间位置的那个数,由中位数的定义可知,这组数据的中位数是9;
故选B.
例题2:
如图,是由大小完全相同的正六边形组成的图形,小军准备用红色、黄色、蓝色随机给每个正六边形分别涂上其中的一种颜色,则上方的正六边形涂红色的概率是 .
【考点】X4:概率公式.
【分析】共有3种情况,上方的正六边形涂红色的情况只有1种,利用概率公式可得答案.
【解答】解:上方的正六边形涂红色的概率是,
故答案为:.
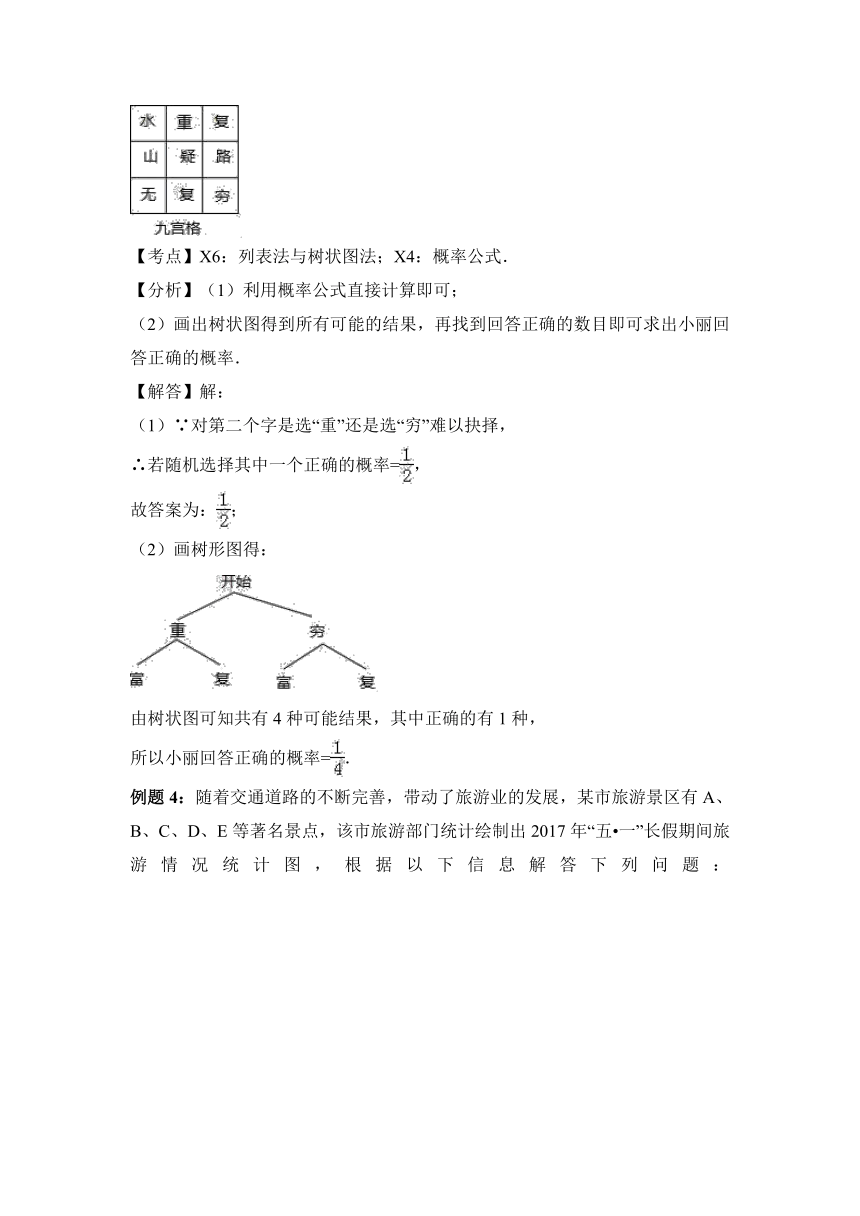
例题3:为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.
【考点】X6:列表法与树状图法;X4:概率公式.
【分析】(1)利用概率公式直接计算即可;
(2)画出树状图得到所有可能的结果,再找到回答正确的数目即可求出小丽回答正确的概率.
【解答】解:
(1)∵对第二个字是选“重”还是选“穷”难以抉择,
∴若随机选择其中一个正确的概率=,
故答案为:;
(2)画树形图得:
由树状图可知共有4种可能结果,其中正确的有1种,
所以小丽回答正确的概率=.
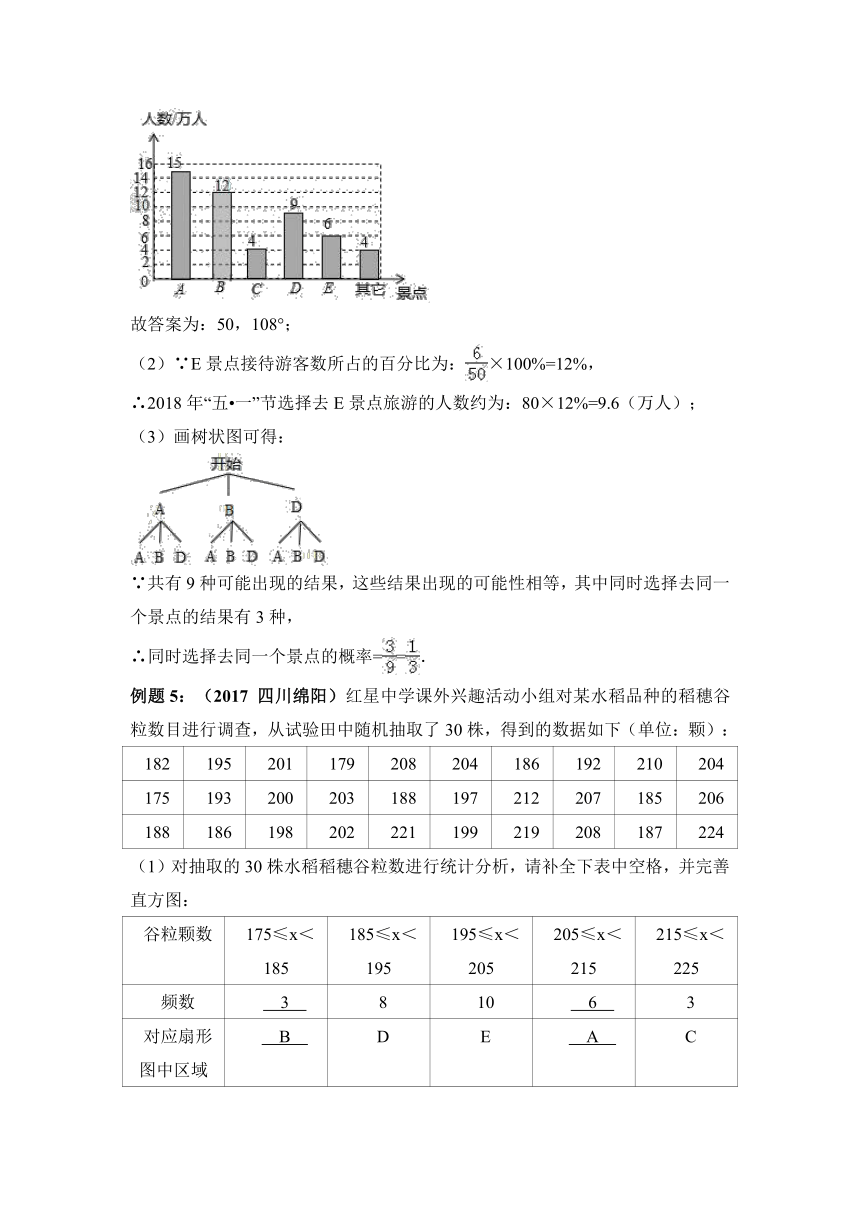
例题4:随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五 一”长假期间旅游情况统计图,根据以下信息解答下列问题:
(1)2017年“五 一”期间,该市周边景点共接待游客 50 万人,扇形统计图中A景点所对应的圆心角的度数是 108° ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五 一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
【考点】X6:列表法与树状图法;V5:用样本估计总体;VB:扇形统计图;VC:条形统计图.
【分析】(1)根据A景点的人数以及百分表进行计算即可得到该市周边景点共接待游客数;先求得A景点所对应的圆心角的度数,再根据扇形圆心角的度数=部分占总体的百分比×360°进行计算即可;根据B景点接待游客数补全条形统计图;
(2)根据E景点接待游客数所占的百分比,即可估计2018年“五 一”节选择去E景点旅游的人数;
(3)根据甲、乙两个旅行团在A、B、D三个景点中各选择一个景点,画出树状图,根据概率公式进行计算,即可得到同时选择去同一景点的概率.
【解答】解:(1)该市周边景点共接待游客数为:15÷30%=50(万人),
A景点所对应的圆心角的度数是:30%×360°=108°,
B景点接待游客数为:50×24%=12(万人),
补全条形统计图如下:
故答案为:50,108°;
(2)∵E景点接待游客数所占的百分比为:×100%=12%,
∴2018年“五 一”节选择去E景点旅游的人数约为:80×12%=9.6(万人);
(3)画树状图可得:
∵共有9种可能出现的结果,这些结果出现的可能性相等,其中同时选择去同一个景点的结果有3种,
∴同时选择去同一个景点的概率==.
例题5:(2017
四川绵阳)红星中学课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
182
195
201
179
208
204
186
192
210
204
175
193
200
203
188
197
212
207
185
206
188
186
198
202
221
199
219
208
187
224
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
谷粒颗数
175≤x<185
185≤x<195
195≤x<205
205≤x<215
215≤x<225
频数
3
8
10
6
3
对应扇形图中区域
B
D
E
A
C
如图所示的扇形统计图中,扇形A对应的圆心角为 72 度,扇形B对应的圆心角为 36 度;
(2)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?
【考点】V8:频数(率)分布直方图;V5:用样本估计总体;V7:频数(率)分布表;VB:扇形统计图.
【分析】(1)根据表格中数据填表画图即可,利用360°×其所占的百分比求出扇形对应的圆心角度数;
(2)用360°乘以样本中稻穗谷粒数大于或等于205颗的水稻所占百分比即可.
【解答】解:(1)填表如下:
谷粒颗数
175≤x<185
185≤x<195
195≤x<205
205≤x<215
215≤x<225
频数
3
8
10
6
3
对应扇形图中区域
B
D
E
A
C
如图所示:
如图所示的扇形统计图中,扇形A对应的圆心角为:360°×=72度,扇形B对应的圆心角为360°×=36度.
故答案为3,6,B,A,72,36;
(2)3000×=900.
即据此估计,其中稻穗谷粒数大于或等于205颗的水稻有900株.
例题6:(2017.四川眉山)一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是.
(1)求袋中红球的个数;
(2)求从袋中任取一个球是黑球的概率.
【考点】X4:概率公式.
【分析】(1)先根据概率公式求出白球的个数为10,进一步求得红、黑两种球的个数和为280,再根据红球个数是黑球个数的2倍多40个,可得黑球个数为÷(2+1)=80个,进一步得到红球的个数;
(2)根据概率公式可求从袋中任取一个球是黑球的概率.
【解答】解:(1)290×=10(个),
290﹣10=280(个),
÷(2+1)=80(个),
280﹣80=200(个).
故袋中红球的个数是200个;
(2)80÷290=.
答:从袋中任取一个球是黑球的概率是.
【达标检测评估】
一、选择题:
1.
(2017.四川眉山)下列说法错误的是( )
A.给定一组数据,那么这组数据的平均数一定只有一个
B.给定一组数据,那么这组数据的中位数一定只有一个
C.给定一组数据,那么这组数据的众数一定只有一个
D.如果一组数据存在众数,那么该众数一定是这组数据中的某一个
【考点】W5:众数;W1:算术平均数;W4:中位数.
【分析】利用平均数、中位数及众数的定义分别判断后即可确定正确的选项.
【解答】解:A、给定一组数据,那么这组数据的平均数一定只有一个,正确,不符合题意;
B、给定一组数据,那么这组数据的中位数一定只有一个,正确,不符合题意;
C、给定一组数据,那么这组数据的众数一定只有一个,错误,符合题意;
D、如果一组数据存在众数,那么该众数一定是这组数据中的某一个,正确,不符合题意,
故选C.
2.
(2017山东临沂)小明和小华玩“石头、剪子、布”的游戏,若随机出手一次,则小华获胜的概率是( )
A.
B.
C.
D.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小华获胜的情况数,再利用概率公式即可求得答案.
【解答】解:画树状图得:
∵共有9种等可能的结果,小华获胜的情况数是3种,
∴小华获胜的概率是:=.
故选C.
【点评】此题主要考查了列表法和树状图法求概率知识,用到的知识点为:概率=所求情况数与总情况数之比.
3.
(2017山东临沂)某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:
部门
人数
每人创年利润(万元)
A
1
10
B
3
8
C
7
5
D
4
3
这15名员工每人所创年利润的众数、中位数分别是( )
A.10,5
B.7,8
C.5,6.5
D.5,5
【分析】根据表格中的数据可以将这组数据按照从小到大的顺序排列起来,从而可以找到这组数据的中位数和众数.
【解答】解:由题意可得,
这15名员工的每人创年利润为:10、8、8、8、5、5、5、5、5、5、5、3、3、3、3,
∴这组数据的众数是5,中位数是5,
故选D.
【点评】本题考查众数和中位数,解答本题的关键是明确众数和中位数的定义,会找一组数据的众数和中位数.
4.
(2017.江苏宿迁)一组数据:5,4,6,5,6,6,3,这组数据的众数是( )
A.6
B.5
C.4
D.3
【考点】W5:众数.
【分析】众数的求法:一组数据中出现次数最多的那个数;据此解答.
【解答】解:因为这组数据中出现次数最多的数是6,
所以6是这组数据的众数;
故选:A.
5.
(2016·山东省济宁市·3分)如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )
A.
B.
C.
D.
【考点】概率公式;利用轴对称设计图案.
【分析】由在4×4正方形网格中,任选取一个白色的小正方形并涂黑,共有13种等可能的结果,使图中黑色部分的图形构成一个轴对称图形的有5种情况,直接利用概率公式求解即可求得答案.
【解答】解:∵根据轴对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合,白色的小正方形有13个,而能构成一个轴对称图形的有4个情况,
∴使图中黑色部分的图形仍然构成一个轴对称图形的概率是:.
故选B.
二、填空题:
6.
(2017
四川绵阳)同时抛掷两枚质地均匀的骰子,则事件“两枚骰子的点数和小于8且为偶数”的概率是 .
【考点】X6:列表法与树状图法.
【分析】画树状图展示所有36种等可能的结果数,再找出“两枚骰子的点数和小于8且为偶数”的结果数,然后根据概率公式求解.
【解答】解:画树状图为:
共有36种等可能的结果数,其中“两枚骰子的点数和小于8且为偶数”的结果数为9,
所以“两枚骰子的点数和小于8且为偶数”的概率==.
故答案为.
7.
已知一组从小到大排列的数据:2,5,x,y,2x,11的平均数与中位数都是7,则这组数据的众数是 5 .
【考点】W5:众数;W1:算术平均数;W4:中位数.
【分析】根据平均数与中位数的定义可以先求出x,y的值,进而就可以确定这组数据的众数即可.
【解答】解:∵一组从小到大排列的数据:2,5,x,y,2x,11的平均数与中位数都是7,
∴(2+5+x+y+2x+11)=(x+y)=7,
解得y=9,x=5,
∴这组数据的众数是5.
故答案为5.
8.
(2017.江苏宿迁)如图,为测量平地上一块不规则区域(图中的阴影部分)的面积,画一个边长为2cm的正方形,使不规则区域落在正方形内,现向正方形内随机投掷小石子(假设小石子落在正方形内每一点都是等可能的),经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数0.25附近,由此可估计不规则区域的面积是 1 m2.
【考点】X8:利用频率估计概率.
【分析】首先确定小石子落在不规则区域的概率,然后利用概率公式求得其面积即可.
【解答】解:∵经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数0.25附近,
∴小石子落在不规则区域的概率为0.25,
∵正方形的边长为2cm,
∴面积为4cm2,
设不规则部分的面积为s,
则=0.25,
解得:s=1,
故答案为:1.
9.
(2017年湖南郴州)为从甲、乙两名射击运动员中选出一人参加市锦标赛,特统计了他们最近10次射击训练的成绩,其中,他们射击的平均成绩都为8.9环,方差分别是S甲2=0.8,S乙2=1.3,从稳定性的角度来看 甲 的成绩更稳定.(填“甲”或“乙”)
【分析】根据方差的意义即可得.
【解答】解:∵S甲2=0.8,S乙2=1.3,
∴S甲2<S乙2,
∴成绩最稳定的运动员是甲,
故答案是:甲.
【点评】本题主要考查方差,熟练掌握方差的意义:方差越小,数据的密集度越高,波动幅度越小是解题的关键.
三、解答题:
10.
(2017山东临沂)为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计9要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:
学生最喜爱的节目人数统计表
节目
人数(名)
百分比
最强大脑
5
10%
朗读者
15
b%
中国诗词大会
a
40%
出彩中国人
10
20%
根据以上提供的信息,解答下列问题:
(1)x= 50 ,a= 20 ,b= 30 ;
(2)补全上面的条形统计图;
(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.
【分析】(1)根据最强大脑的人数除以占的百分比确定出x的值,进而求出a与b的值即可;
(2)根据a的值,补全条形统计图即可;
(3)由中国诗词大会的百分比乘以1000即可得到结果.
【解答】解:(1)根据题意得:x=5÷10%=50,a=50×40%=20,b=×100=30;
故答案为:50;20;30;
(2)中国诗词大会的人数为20人,补全条形统计图,如图所示:
(3)根据题意得:1000×40%=400(名),
则估计该校最喜爱《中国诗词大会》节目的学生有400名.
【点评】此题考查了条形统计图,用样本估计总体,以及统计表,弄清题中的数据是解本题的关键.
11.
“大美湿地,水韵盐城”.某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:
请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有800名学生,请估计“最想去景点B“的学生人数.
【考点】VC:条形统计图;V5:用样本估计总体;VB:扇形统计图.
【分析】(1)用最想去A景点的人数除以它所占的百分比即可得到被调查的学生总人数;
(2)先计算出最想去D景点的人数,再补全条形统计图,然后用360°乘以最想去D景点的人数所占的百分比即可得到扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)用800乘以样本中最想去A景点的人数所占的百分比即可.
【解答】解:(1)被调查的学生总人数为8÷20%=40(人);
(2)最想去D景点的人数为40﹣8﹣14﹣4﹣6=8(人),
补全条形统计图为:
扇形统计图中表示“最想去景点D”的扇形圆心角的度数为×360°=72°;
(3)800×=280,
所以估计“最想去景点B“的学生人数为280人.
12.
(2017湖北宜昌)YC市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够,导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
请回答下列问题:
时间
第一天7:00﹣8:00
第二天7:00﹣8:00
第三天7:00﹣8:00
第四天7:00﹣8:00
第五天7:00﹣8:00
需要租用自行车却未租到车的人数(人)
1500
1200
1300
1300
1200
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00﹣8:00:需要租用公共自行车的人数是多少?
【考点】W4:中位数;V5:用样本估计总体.
【分析】(1)表格中5个数据按从小到大的顺序排列后,中位数应是第3个数据;
(2)根据平均数等于数据之和除以总个数求出平均每天需要租用自行车却未租到车的人数,再加上700即可.
【解答】解:(1)表格中5个数据按从小到大的顺序排列为1200,1200,1300,1300,1500,
所以中位数是1300;
(2)平均每天需要租用自行车却未租到车的人数:÷5=1300,
∵YC市首批一次性投放公共自行车700辆供市民租用出行,
∴平均每天需要租用公共自行车的人数是1300+700=2000.
13.
在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转运甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
【考点】X6:列表法与树状图法.
【分析】(1)根据题意列出表格,得出游戏中两数和的所有可能的结果数;
(2)根据(1)得出两数和共有的情况数和其中和小于12的情况、和大于12的情况数,再根据概率公式即可得出答案.
【解答】解:(1)根据题意列表如下:
甲
乙
6
7
8
9
3
9
10
11
12
4
10
11
12
13
5
11
12
13
14
可见,两数和共有12种等可能性;
(2)由(1)可知,两数和共有12种等可能的情况,其中和小于12的情况有6种,和大于12的情况有3种,
∴李燕获胜的概率为=;
刘凯获胜的概率为=.
【专题知识结构】
【专题解题分析】
统计与概率在中考中的常考点有数据的收集方法,平均数、众数和中位数的计算与选择,方差和标准差的计算和应用,统计图的应用及信息综合分析;事件的分类,简单事件的概率计算,画树状图或列表求概率,对频率和概率的理解等.统计与概率在中考中一般以客观题的形式进行考查,选择题、填空题较多,同时考查多个考点的综合性题目一般以解答题的形式进行考查;
解决统计与概率问题常用的数学思想是方程思想和分类讨论思想;常用的数学方法有分类讨论法,整体代入法等.
【典型例题解析】
例题1:
如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A.16,10.5
B.8,9
C.16,8.5
D.8,8.5
【考点】W5:众数;VC:条形统计图;W4:中位数.
【分析】根据中位数、众数的概念分别求得这组数据的中位数、众数,由图可知锻炼时间超过8小时的有14+7=21人.
【解答】解:众数是一组数据中出现次数最多的数,即8;
而将这组数据从小到大的顺序排列后,处于中间位置的那个数,由中位数的定义可知,这组数据的中位数是9;
故选B.
例题2:
如图,是由大小完全相同的正六边形组成的图形,小军准备用红色、黄色、蓝色随机给每个正六边形分别涂上其中的一种颜色,则上方的正六边形涂红色的概率是 .
【考点】X4:概率公式.
【分析】共有3种情况,上方的正六边形涂红色的情况只有1种,利用概率公式可得答案.
【解答】解:上方的正六边形涂红色的概率是,
故答案为:.
例题3:为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.
【考点】X6:列表法与树状图法;X4:概率公式.
【分析】(1)利用概率公式直接计算即可;
(2)画出树状图得到所有可能的结果,再找到回答正确的数目即可求出小丽回答正确的概率.
【解答】解:
(1)∵对第二个字是选“重”还是选“穷”难以抉择,
∴若随机选择其中一个正确的概率=,
故答案为:;
(2)画树形图得:
由树状图可知共有4种可能结果,其中正确的有1种,
所以小丽回答正确的概率=.
例题4:随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五 一”长假期间旅游情况统计图,根据以下信息解答下列问题:
(1)2017年“五 一”期间,该市周边景点共接待游客 50 万人,扇形统计图中A景点所对应的圆心角的度数是 108° ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五 一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
【考点】X6:列表法与树状图法;V5:用样本估计总体;VB:扇形统计图;VC:条形统计图.
【分析】(1)根据A景点的人数以及百分表进行计算即可得到该市周边景点共接待游客数;先求得A景点所对应的圆心角的度数,再根据扇形圆心角的度数=部分占总体的百分比×360°进行计算即可;根据B景点接待游客数补全条形统计图;
(2)根据E景点接待游客数所占的百分比,即可估计2018年“五 一”节选择去E景点旅游的人数;
(3)根据甲、乙两个旅行团在A、B、D三个景点中各选择一个景点,画出树状图,根据概率公式进行计算,即可得到同时选择去同一景点的概率.
【解答】解:(1)该市周边景点共接待游客数为:15÷30%=50(万人),
A景点所对应的圆心角的度数是:30%×360°=108°,
B景点接待游客数为:50×24%=12(万人),
补全条形统计图如下:
故答案为:50,108°;
(2)∵E景点接待游客数所占的百分比为:×100%=12%,
∴2018年“五 一”节选择去E景点旅游的人数约为:80×12%=9.6(万人);
(3)画树状图可得:
∵共有9种可能出现的结果,这些结果出现的可能性相等,其中同时选择去同一个景点的结果有3种,
∴同时选择去同一个景点的概率==.
例题5:(2017
四川绵阳)红星中学课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
182
195
201
179
208
204
186
192
210
204
175
193
200
203
188
197
212
207
185
206
188
186
198
202
221
199
219
208
187
224
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
谷粒颗数
175≤x<185
185≤x<195
195≤x<205
205≤x<215
215≤x<225
频数
3
8
10
6
3
对应扇形图中区域
B
D
E
A
C
如图所示的扇形统计图中,扇形A对应的圆心角为 72 度,扇形B对应的圆心角为 36 度;
(2)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?
【考点】V8:频数(率)分布直方图;V5:用样本估计总体;V7:频数(率)分布表;VB:扇形统计图.
【分析】(1)根据表格中数据填表画图即可,利用360°×其所占的百分比求出扇形对应的圆心角度数;
(2)用360°乘以样本中稻穗谷粒数大于或等于205颗的水稻所占百分比即可.
【解答】解:(1)填表如下:
谷粒颗数
175≤x<185
185≤x<195
195≤x<205
205≤x<215
215≤x<225
频数
3
8
10
6
3
对应扇形图中区域
B
D
E
A
C
如图所示:
如图所示的扇形统计图中,扇形A对应的圆心角为:360°×=72度,扇形B对应的圆心角为360°×=36度.
故答案为3,6,B,A,72,36;
(2)3000×=900.
即据此估计,其中稻穗谷粒数大于或等于205颗的水稻有900株.
例题6:(2017.四川眉山)一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是.
(1)求袋中红球的个数;
(2)求从袋中任取一个球是黑球的概率.
【考点】X4:概率公式.
【分析】(1)先根据概率公式求出白球的个数为10,进一步求得红、黑两种球的个数和为280,再根据红球个数是黑球个数的2倍多40个,可得黑球个数为÷(2+1)=80个,进一步得到红球的个数;
(2)根据概率公式可求从袋中任取一个球是黑球的概率.
【解答】解:(1)290×=10(个),
290﹣10=280(个),
÷(2+1)=80(个),
280﹣80=200(个).
故袋中红球的个数是200个;
(2)80÷290=.
答:从袋中任取一个球是黑球的概率是.
【达标检测评估】
一、选择题:
1.
(2017.四川眉山)下列说法错误的是( )
A.给定一组数据,那么这组数据的平均数一定只有一个
B.给定一组数据,那么这组数据的中位数一定只有一个
C.给定一组数据,那么这组数据的众数一定只有一个
D.如果一组数据存在众数,那么该众数一定是这组数据中的某一个
【考点】W5:众数;W1:算术平均数;W4:中位数.
【分析】利用平均数、中位数及众数的定义分别判断后即可确定正确的选项.
【解答】解:A、给定一组数据,那么这组数据的平均数一定只有一个,正确,不符合题意;
B、给定一组数据,那么这组数据的中位数一定只有一个,正确,不符合题意;
C、给定一组数据,那么这组数据的众数一定只有一个,错误,符合题意;
D、如果一组数据存在众数,那么该众数一定是这组数据中的某一个,正确,不符合题意,
故选C.
2.
(2017山东临沂)小明和小华玩“石头、剪子、布”的游戏,若随机出手一次,则小华获胜的概率是( )
A.
B.
C.
D.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小华获胜的情况数,再利用概率公式即可求得答案.
【解答】解:画树状图得:
∵共有9种等可能的结果,小华获胜的情况数是3种,
∴小华获胜的概率是:=.
故选C.
【点评】此题主要考查了列表法和树状图法求概率知识,用到的知识点为:概率=所求情况数与总情况数之比.
3.
(2017山东临沂)某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:
部门
人数
每人创年利润(万元)
A
1
10
B
3
8
C
7
5
D
4
3
这15名员工每人所创年利润的众数、中位数分别是( )
A.10,5
B.7,8
C.5,6.5
D.5,5
【分析】根据表格中的数据可以将这组数据按照从小到大的顺序排列起来,从而可以找到这组数据的中位数和众数.
【解答】解:由题意可得,
这15名员工的每人创年利润为:10、8、8、8、5、5、5、5、5、5、5、3、3、3、3,
∴这组数据的众数是5,中位数是5,
故选D.
【点评】本题考查众数和中位数,解答本题的关键是明确众数和中位数的定义,会找一组数据的众数和中位数.
4.
(2017.江苏宿迁)一组数据:5,4,6,5,6,6,3,这组数据的众数是( )
A.6
B.5
C.4
D.3
【考点】W5:众数.
【分析】众数的求法:一组数据中出现次数最多的那个数;据此解答.
【解答】解:因为这组数据中出现次数最多的数是6,
所以6是这组数据的众数;
故选:A.
5.
(2016·山东省济宁市·3分)如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )
A.
B.
C.
D.
【考点】概率公式;利用轴对称设计图案.
【分析】由在4×4正方形网格中,任选取一个白色的小正方形并涂黑,共有13种等可能的结果,使图中黑色部分的图形构成一个轴对称图形的有5种情况,直接利用概率公式求解即可求得答案.
【解答】解:∵根据轴对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合,白色的小正方形有13个,而能构成一个轴对称图形的有4个情况,
∴使图中黑色部分的图形仍然构成一个轴对称图形的概率是:.
故选B.
二、填空题:
6.
(2017
四川绵阳)同时抛掷两枚质地均匀的骰子,则事件“两枚骰子的点数和小于8且为偶数”的概率是 .
【考点】X6:列表法与树状图法.
【分析】画树状图展示所有36种等可能的结果数,再找出“两枚骰子的点数和小于8且为偶数”的结果数,然后根据概率公式求解.
【解答】解:画树状图为:
共有36种等可能的结果数,其中“两枚骰子的点数和小于8且为偶数”的结果数为9,
所以“两枚骰子的点数和小于8且为偶数”的概率==.
故答案为.
7.
已知一组从小到大排列的数据:2,5,x,y,2x,11的平均数与中位数都是7,则这组数据的众数是 5 .
【考点】W5:众数;W1:算术平均数;W4:中位数.
【分析】根据平均数与中位数的定义可以先求出x,y的值,进而就可以确定这组数据的众数即可.
【解答】解:∵一组从小到大排列的数据:2,5,x,y,2x,11的平均数与中位数都是7,
∴(2+5+x+y+2x+11)=(x+y)=7,
解得y=9,x=5,
∴这组数据的众数是5.
故答案为5.
8.
(2017.江苏宿迁)如图,为测量平地上一块不规则区域(图中的阴影部分)的面积,画一个边长为2cm的正方形,使不规则区域落在正方形内,现向正方形内随机投掷小石子(假设小石子落在正方形内每一点都是等可能的),经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数0.25附近,由此可估计不规则区域的面积是 1 m2.
【考点】X8:利用频率估计概率.
【分析】首先确定小石子落在不规则区域的概率,然后利用概率公式求得其面积即可.
【解答】解:∵经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数0.25附近,
∴小石子落在不规则区域的概率为0.25,
∵正方形的边长为2cm,
∴面积为4cm2,
设不规则部分的面积为s,
则=0.25,
解得:s=1,
故答案为:1.
9.
(2017年湖南郴州)为从甲、乙两名射击运动员中选出一人参加市锦标赛,特统计了他们最近10次射击训练的成绩,其中,他们射击的平均成绩都为8.9环,方差分别是S甲2=0.8,S乙2=1.3,从稳定性的角度来看 甲 的成绩更稳定.(填“甲”或“乙”)
【分析】根据方差的意义即可得.
【解答】解:∵S甲2=0.8,S乙2=1.3,
∴S甲2<S乙2,
∴成绩最稳定的运动员是甲,
故答案是:甲.
【点评】本题主要考查方差,熟练掌握方差的意义:方差越小,数据的密集度越高,波动幅度越小是解题的关键.
三、解答题:
10.
(2017山东临沂)为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计9要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:
学生最喜爱的节目人数统计表
节目
人数(名)
百分比
最强大脑
5
10%
朗读者
15
b%
中国诗词大会
a
40%
出彩中国人
10
20%
根据以上提供的信息,解答下列问题:
(1)x= 50 ,a= 20 ,b= 30 ;
(2)补全上面的条形统计图;
(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.
【分析】(1)根据最强大脑的人数除以占的百分比确定出x的值,进而求出a与b的值即可;
(2)根据a的值,补全条形统计图即可;
(3)由中国诗词大会的百分比乘以1000即可得到结果.
【解答】解:(1)根据题意得:x=5÷10%=50,a=50×40%=20,b=×100=30;
故答案为:50;20;30;
(2)中国诗词大会的人数为20人,补全条形统计图,如图所示:
(3)根据题意得:1000×40%=400(名),
则估计该校最喜爱《中国诗词大会》节目的学生有400名.
【点评】此题考查了条形统计图,用样本估计总体,以及统计表,弄清题中的数据是解本题的关键.
11.
“大美湿地,水韵盐城”.某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:
请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有800名学生,请估计“最想去景点B“的学生人数.
【考点】VC:条形统计图;V5:用样本估计总体;VB:扇形统计图.
【分析】(1)用最想去A景点的人数除以它所占的百分比即可得到被调查的学生总人数;
(2)先计算出最想去D景点的人数,再补全条形统计图,然后用360°乘以最想去D景点的人数所占的百分比即可得到扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)用800乘以样本中最想去A景点的人数所占的百分比即可.
【解答】解:(1)被调查的学生总人数为8÷20%=40(人);
(2)最想去D景点的人数为40﹣8﹣14﹣4﹣6=8(人),
补全条形统计图为:
扇形统计图中表示“最想去景点D”的扇形圆心角的度数为×360°=72°;
(3)800×=280,
所以估计“最想去景点B“的学生人数为280人.
12.
(2017湖北宜昌)YC市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够,导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
请回答下列问题:
时间
第一天7:00﹣8:00
第二天7:00﹣8:00
第三天7:00﹣8:00
第四天7:00﹣8:00
第五天7:00﹣8:00
需要租用自行车却未租到车的人数(人)
1500
1200
1300
1300
1200
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00﹣8:00:需要租用公共自行车的人数是多少?
【考点】W4:中位数;V5:用样本估计总体.
【分析】(1)表格中5个数据按从小到大的顺序排列后,中位数应是第3个数据;
(2)根据平均数等于数据之和除以总个数求出平均每天需要租用自行车却未租到车的人数,再加上700即可.
【解答】解:(1)表格中5个数据按从小到大的顺序排列为1200,1200,1300,1300,1500,
所以中位数是1300;
(2)平均每天需要租用自行车却未租到车的人数:÷5=1300,
∵YC市首批一次性投放公共自行车700辆供市民租用出行,
∴平均每天需要租用公共自行车的人数是1300+700=2000.
13.
在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转运甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
【考点】X6:列表法与树状图法.
【分析】(1)根据题意列出表格,得出游戏中两数和的所有可能的结果数;
(2)根据(1)得出两数和共有的情况数和其中和小于12的情况、和大于12的情况数,再根据概率公式即可得出答案.
【解答】解:(1)根据题意列表如下:
甲
乙
6
7
8
9
3
9
10
11
12
4
10
11
12
13
5
11
12
13
14
可见,两数和共有12种等可能性;
(2)由(1)可知,两数和共有12种等可能的情况,其中和小于12的情况有6种,和大于12的情况有3种,
∴李燕获胜的概率为=;
刘凯获胜的概率为=.
同课章节目录
