人教九年级上册数学22.1二次函数图像与性质 复习课件
文档属性
| 名称 | 人教九年级上册数学22.1二次函数图像与性质 复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 194.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-22 08:15:07 | ||
图片预览






文档简介
课件17张PPT。二次函数图像与性质
复习课
一般地,形如 y=ax2+bx+c
(a,b,c 是常数,a≠0)的函数,叫做
二次函数. 其中,x是自变量,a , b , c分别是二次项系数、一次项系数和常数项.例:若函数 是关于x的二次函数,求
⑴m=?
⑵m为何值时,抛物线有最低点?求出这个最低点坐标; 这时当x为何值时,y随着x的增大而增大?
⑶m为何值时,函数有最大值?最大值是什么? 这时当x为何值时,y随着x的增大而增大?
⑥ 2a-b 0;
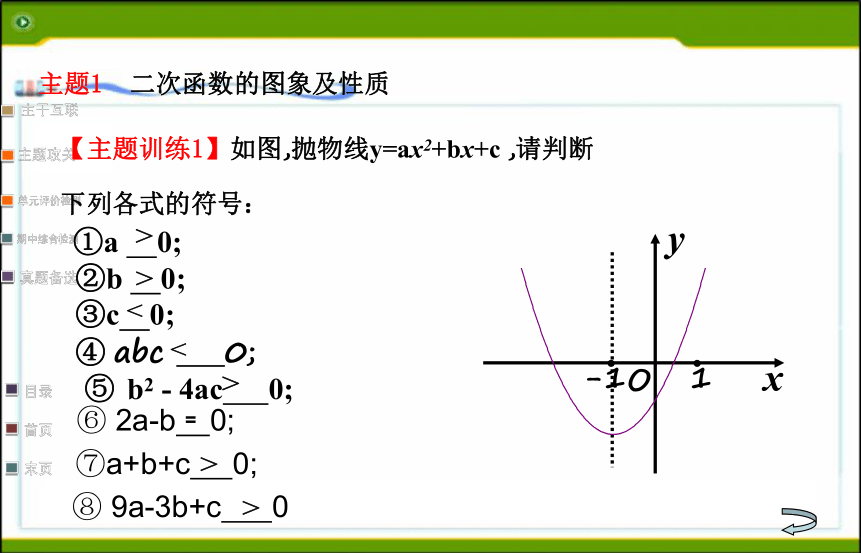
【主题训练1】如图,抛物线y=ax2+bx+c ,请判断
下列各式的符号:
①a 0;
②b 0;
③c 0;
④ abc 0;
⑤ b2 - 4ac 0;
><>>⑦a+b+c 0;⑧ 9a-3b+c 0<>=主题1 二次函数的图象及性质>1.已知二次函数y=x2+bx+c的图象过点A(1,m),
B(3,m),若点M(﹣2,y1),N(﹣1,y2),
K(8,y3)也在二次函数y=x2+bx+c的图象上,则下列结论正确的是( )
A. y1<y2<y3 B. y2<y1<y3
C. y3<y1<y2 D. y2 <y3< y1B【方法技巧】二次函数比较大小的三种方法
1.代入数值计算函数值比较大小.
2.在对称轴的同侧根据函数的增减性比较大小.
3.在对称轴的异侧根据开口方向和距对称轴距离的远近比较大小.2.已知二次函数y=x2+bx+c的图象过点A(-5,y1),
B(3,y2),点C0(x0,y0)是该抛物线的顶点,若 y1 > y2 > yo ,则x0的取值范围是( )
A.x0 >-5 ; B. x0 >-1 ;
C.-5< x0 <-1; D.-2 <x0 <3B【知识延伸】y=ax2+bx+c -—→y=a(x+ )2+ [回顾一般式与顶点式关系]主题2 二次函数的平移
【主题训练2】将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )
A.y=3(x+2)2+3 B.y=3(x-2)2+3
C.y=3(x+2)2-3 D.y=3(x-2)2-3A1.下列二次函数的图象,不能通过函数y=3x2的图象平移得到的是( )
A.y=3x2+2 B.y=3(x-1)2
C.y=3(x-1)2+2 D.y=2x2D2.抛物线y=x2+bx+c的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为y=(x-1)2-4,则b,c的值为( )
A.b=2,c=-6 B.b=2,c=0
C.b=-6,c=8 D.b=-6,c=2B【知识延伸】1.把抛物线y=(x-1)2-4绕着它的顶点旋转1800 ,得到:2.把抛物线y=(x-1)2-4沿着x轴翻折 ,得到:3.把抛物线y=(x-1)2-4沿着y轴翻折 ,得到:y=-(x-1)2 -4y=-(x-1)2 +4y=(x+1)2 -4【知识归纳】二次函数之间的平移关系
1.二次函数y=ax2先向右平移h(h>0)个单位,再向上平移k(k>0)个单位得二次函数
2.二次函数y=a(x-h)2+k先向下平移k(k>0)个单位,再向左平移h(h>0)个单位得二次函数y=a(x-h)2 +ky=ax2主题3 二次函数的应用
【主题训练3】科幻小说《实验室的故事》中,有这样一个情节:科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如表).由这些数据,科学家推测出植物每天高度增长量y是温度x的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由.
(2)温度为多少时,这种植物每天高度增长量最大?【自主解答】(1)选择二次函数.设抛物线的解析式为y=ax2+bx+c,
根据题意,得
∴y关于x的函数解析式为y=-x2-2x+49.
不选另外两个函数的理由:点(0,49)不可能在任何反比例函数图象上,所以y不是x的反比例函数;点(-4,41),(-2,49),(2,41)不在同一直线上,所以y不是x的一次函数.(2)由(1)得y=-x2-2x+49,∴y=-(x+1)2+50.
∵a=-1<0,∴当x=-1时y的最大值为50.
即当温度为-1℃时,这种植物每天高度增长量最大.谢谢指导
复习课
一般地,形如 y=ax2+bx+c
(a,b,c 是常数,a≠0)的函数,叫做
二次函数. 其中,x是自变量,a , b , c分别是二次项系数、一次项系数和常数项.例:若函数 是关于x的二次函数,求
⑴m=?
⑵m为何值时,抛物线有最低点?求出这个最低点坐标; 这时当x为何值时,y随着x的增大而增大?
⑶m为何值时,函数有最大值?最大值是什么? 这时当x为何值时,y随着x的增大而增大?
⑥ 2a-b 0;
【主题训练1】如图,抛物线y=ax2+bx+c ,请判断
下列各式的符号:
①a 0;
②b 0;
③c 0;
④ abc 0;
⑤ b2 - 4ac 0;
><>>⑦a+b+c 0;⑧ 9a-3b+c 0<>=主题1 二次函数的图象及性质>1.已知二次函数y=x2+bx+c的图象过点A(1,m),
B(3,m),若点M(﹣2,y1),N(﹣1,y2),
K(8,y3)也在二次函数y=x2+bx+c的图象上,则下列结论正确的是( )
A. y1<y2<y3 B. y2<y1<y3
C. y3<y1<y2 D. y2 <y3< y1B【方法技巧】二次函数比较大小的三种方法
1.代入数值计算函数值比较大小.
2.在对称轴的同侧根据函数的增减性比较大小.
3.在对称轴的异侧根据开口方向和距对称轴距离的远近比较大小.2.已知二次函数y=x2+bx+c的图象过点A(-5,y1),
B(3,y2),点C0(x0,y0)是该抛物线的顶点,若 y1 > y2 > yo ,则x0的取值范围是( )
A.x0 >-5 ; B. x0 >-1 ;
C.-5< x0 <-1; D.-2 <x0 <3B【知识延伸】y=ax2+bx+c -—→y=a(x+ )2+ [回顾一般式与顶点式关系]主题2 二次函数的平移
【主题训练2】将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )
A.y=3(x+2)2+3 B.y=3(x-2)2+3
C.y=3(x+2)2-3 D.y=3(x-2)2-3A1.下列二次函数的图象,不能通过函数y=3x2的图象平移得到的是( )
A.y=3x2+2 B.y=3(x-1)2
C.y=3(x-1)2+2 D.y=2x2D2.抛物线y=x2+bx+c的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为y=(x-1)2-4,则b,c的值为( )
A.b=2,c=-6 B.b=2,c=0
C.b=-6,c=8 D.b=-6,c=2B【知识延伸】1.把抛物线y=(x-1)2-4绕着它的顶点旋转1800 ,得到:2.把抛物线y=(x-1)2-4沿着x轴翻折 ,得到:3.把抛物线y=(x-1)2-4沿着y轴翻折 ,得到:y=-(x-1)2 -4y=-(x-1)2 +4y=(x+1)2 -4【知识归纳】二次函数之间的平移关系
1.二次函数y=ax2先向右平移h(h>0)个单位,再向上平移k(k>0)个单位得二次函数
2.二次函数y=a(x-h)2+k先向下平移k(k>0)个单位,再向左平移h(h>0)个单位得二次函数y=a(x-h)2 +ky=ax2主题3 二次函数的应用
【主题训练3】科幻小说《实验室的故事》中,有这样一个情节:科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如表).由这些数据,科学家推测出植物每天高度增长量y是温度x的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由.
(2)温度为多少时,这种植物每天高度增长量最大?【自主解答】(1)选择二次函数.设抛物线的解析式为y=ax2+bx+c,
根据题意,得
∴y关于x的函数解析式为y=-x2-2x+49.
不选另外两个函数的理由:点(0,49)不可能在任何反比例函数图象上,所以y不是x的反比例函数;点(-4,41),(-2,49),(2,41)不在同一直线上,所以y不是x的一次函数.(2)由(1)得y=-x2-2x+49,∴y=-(x+1)2+50.
∵a=-1<0,∴当x=-1时y的最大值为50.
即当温度为-1℃时,这种植物每天高度增长量最大.谢谢指导
同课章节目录
