2017年秋人教版八数上15.2.2 第2课时 分式的混合运算学案(无答案)
文档属性
| 名称 | 2017年秋人教版八数上15.2.2 第2课时 分式的混合运算学案(无答案) | 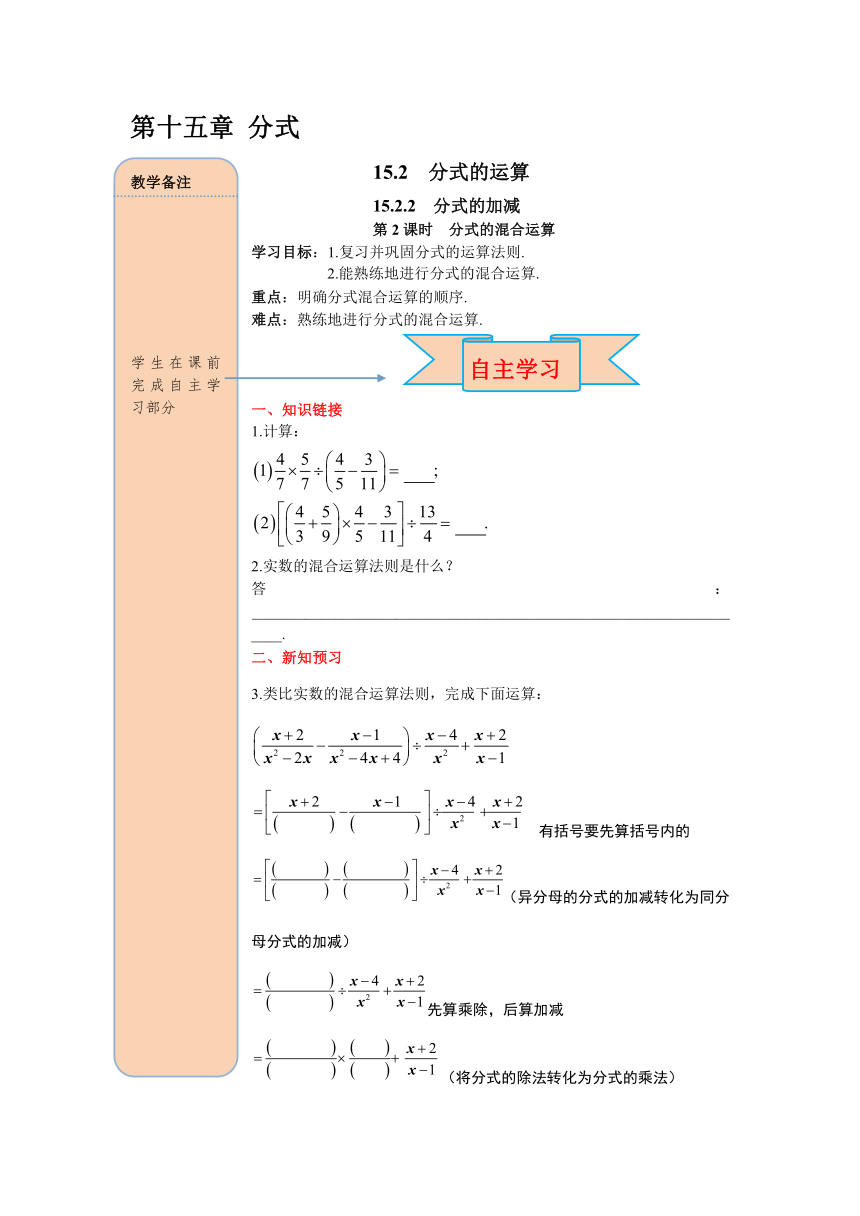 | |
| 格式 | zip | ||
| 文件大小 | 152.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-22 08:35:14 | ||
图片预览


文档简介
第十五章
分式
15.2
分式的运算
15.2.2
分式的加减
第2课时
分式的混合运算
学习目标:1.复习并巩固分式的运算法则.
能熟练地进行分式的混合运算.
重点:明确分式混合运算的顺序.
难点:熟练地进行分式的混合运算.
一、知识链接
1.计算:
实数的混合运算法则是什么?
答:___________________________________________________________________.
二、新知预习
3.类比实数的混合运算法则,完成下面运算:
有括号要先算括号内的
(异分母的分式的加减转化为同分母分式的加减)
先算乘除,后算加减
(将分式的除法转化为分式的乘法)
(异分母的分式的加减转化为同分母分式的加减)
要点归纳:
在进行分式的加、减、乘、除混合运算时,一般
( http: / / www.21cnjy.com )按照运算顺序进行:先算_______,再算_______;如果有括号,先算____________.
三、自学自测
1.计算:
2..先化简,再求值:,其中x=4.
四、我的疑惑
_____________________________________________________________________________________________________________________________________________________
要点探究
探究点:分式的混合运算
问题:如何计算
?请先思考这道题包含的运算,确定运算顺序,再独立完成.
要点归纳:分式的混合运算顺序先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.计算结果要化为最简分式或整式.
典例精析
例1:计算:
方法总结:(1)当式子中出现整式时,把整式看成整体,并把分母看做“1”;
(2)分子或分母是多项式的先因式分解,不能分解的要视为整体.
典例精析
例2:计算:
方法总结:观察题目的结构特点,灵活运用运算律,适当运用计算技巧,可简化运算,提高速度.
例3:计算
方法总结:把
和看成整体,题目的实质是平方差公式的应用.
例4:先化简代数式÷(1-),再从-4<x<4的范围内选取一个合适的整数x代入求值.
方法总结:把分式化成最简分式是解题的关键,通分、因式分解和约分是基本环节,注意选数时,要求分母不能为0.
例5:繁分式的化简:
方法总结:1.把繁分式些成分子除以分母的形式,利用除法法则化简;2.
利用分式的基本性质化简.
针对训练
计算:(1);(2)
二、课堂小结
内容
解题策略
分式的混合运算
先________,再__
( http: / / www.21cnjy.com )______,然后________,有括号的先算括号里面的.最后结果中分子、分母要进行约分,注意运算的结果要化成____________或整式.
分式的混合运算,在运算过程中要注意观察,可灵活运用交换律、结合律、分配律可使运算过程变得更简便.
1.
计算
的结果是(
)
A.
B.
C.
D.
2.
化简的结果是
.
3.
化简的结果是
.
4.计算:
5.
先化简:
,当b=3时,再从-2合适的整数a代入求值.
教学备注
学生在课前完成自主学习部分
自主学习
教学备注
配套PPT讲授
1.问题引入
(见幻灯片3)
2.探究点1新知讲授
(见幻灯片4-21)
课堂探究
教学备注
2.探究点1新知讲授
(见幻灯片4-21)
教学备注
配套PPT讲授
4.课堂小结
5.当堂检测
(见幻灯片22-24)
当堂检测
分式
15.2
分式的运算
15.2.2
分式的加减
第2课时
分式的混合运算
学习目标:1.复习并巩固分式的运算法则.
能熟练地进行分式的混合运算.
重点:明确分式混合运算的顺序.
难点:熟练地进行分式的混合运算.
一、知识链接
1.计算:
实数的混合运算法则是什么?
答:___________________________________________________________________.
二、新知预习
3.类比实数的混合运算法则,完成下面运算:
有括号要先算括号内的
(异分母的分式的加减转化为同分母分式的加减)
先算乘除,后算加减
(将分式的除法转化为分式的乘法)
(异分母的分式的加减转化为同分母分式的加减)
要点归纳:
在进行分式的加、减、乘、除混合运算时,一般
( http: / / www.21cnjy.com )按照运算顺序进行:先算_______,再算_______;如果有括号,先算____________.
三、自学自测
1.计算:
2..先化简,再求值:,其中x=4.
四、我的疑惑
_____________________________________________________________________________________________________________________________________________________
要点探究
探究点:分式的混合运算
问题:如何计算
?请先思考这道题包含的运算,确定运算顺序,再独立完成.
要点归纳:分式的混合运算顺序先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.计算结果要化为最简分式或整式.
典例精析
例1:计算:
方法总结:(1)当式子中出现整式时,把整式看成整体,并把分母看做“1”;
(2)分子或分母是多项式的先因式分解,不能分解的要视为整体.
典例精析
例2:计算:
方法总结:观察题目的结构特点,灵活运用运算律,适当运用计算技巧,可简化运算,提高速度.
例3:计算
方法总结:把
和看成整体,题目的实质是平方差公式的应用.
例4:先化简代数式÷(1-),再从-4<x<4的范围内选取一个合适的整数x代入求值.
方法总结:把分式化成最简分式是解题的关键,通分、因式分解和约分是基本环节,注意选数时,要求分母不能为0.
例5:繁分式的化简:
方法总结:1.把繁分式些成分子除以分母的形式,利用除法法则化简;2.
利用分式的基本性质化简.
针对训练
计算:(1);(2)
二、课堂小结
内容
解题策略
分式的混合运算
先________,再__
( http: / / www.21cnjy.com )______,然后________,有括号的先算括号里面的.最后结果中分子、分母要进行约分,注意运算的结果要化成____________或整式.
分式的混合运算,在运算过程中要注意观察,可灵活运用交换律、结合律、分配律可使运算过程变得更简便.
1.
计算
的结果是(
)
A.
B.
C.
D.
2.
化简的结果是
.
3.
化简的结果是
.
4.计算:
5.
先化简:
,当b=3时,再从-2
教学备注
学生在课前完成自主学习部分
自主学习
教学备注
配套PPT讲授
1.问题引入
(见幻灯片3)
2.探究点1新知讲授
(见幻灯片4-21)
课堂探究
教学备注
2.探究点1新知讲授
(见幻灯片4-21)
教学备注
配套PPT讲授
4.课堂小结
5.当堂检测
(见幻灯片22-24)
当堂检测
