2017年秋冀教版八年级数学上册第16章轴对称和中心对称 章末检测卷(含答案)
文档属性
| 名称 | 2017年秋冀教版八年级数学上册第16章轴对称和中心对称 章末检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 410.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-22 12:17:13 | ||
图片预览

文档简介
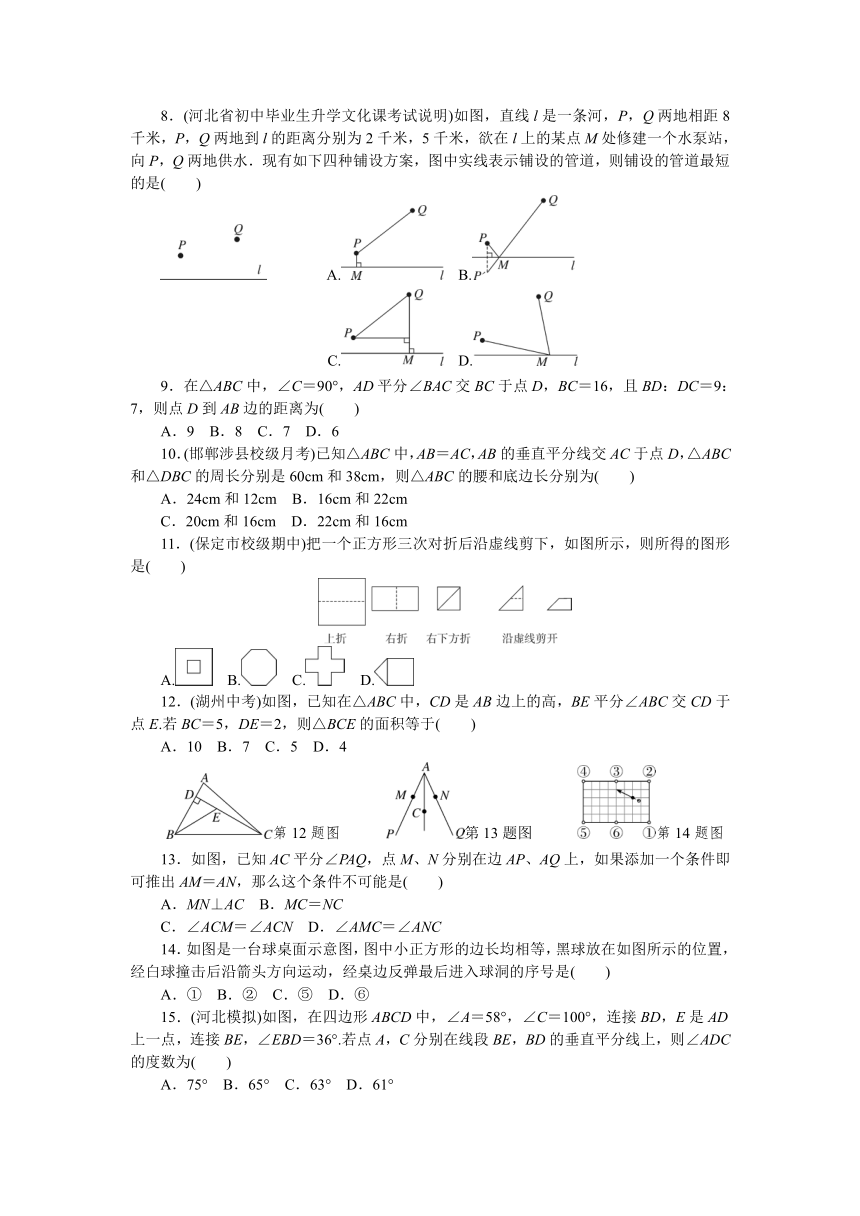
第十六章检测卷
时间:120分钟 满分:120分
班级:__________ 姓名:__________ 得分:__________
一、选择题(第1~10小题,每小题3分,第11~16小题每小题2分,共42分)
1.(保定市涞水县期末)涞水的文化底蕴深厚,涞水人民的生活健康向上.下面的四幅简笔画是从涞水的文化活动中抽象出来的,其中是轴对称图形的是( )
A.
B.
C.
D.
2.(大庆中考)以下图形中对称轴的数量小于3的是( )
3.(河北省初中毕业生升学文化课考试说明)如图,△ABC与△DEF关于直线l对称,则∠E的度数是( )
A.30°
B.50°
C.90°
D.100°
第3题图 第5题图
4.(衡水故城县校级月考)下列四幅图案在设计中用到平移变换方式的是( )
A.
B.
C.
D.
5.如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC中线的交点
B.△ABC三条角平分线的交点
C.△ABC三条高所在的直线交点
D.△ABC三边的中垂线的交点
6.(河北模拟)如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与A′是对应点
B.BO=B′O
C.AB∥A′B′
D.∠ABC=∠B′A′C′
第6题图 第7题图
7.如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于18cm,则AC的长等于( )
A.6cm
B.8cm
C.10cm
D.12cm
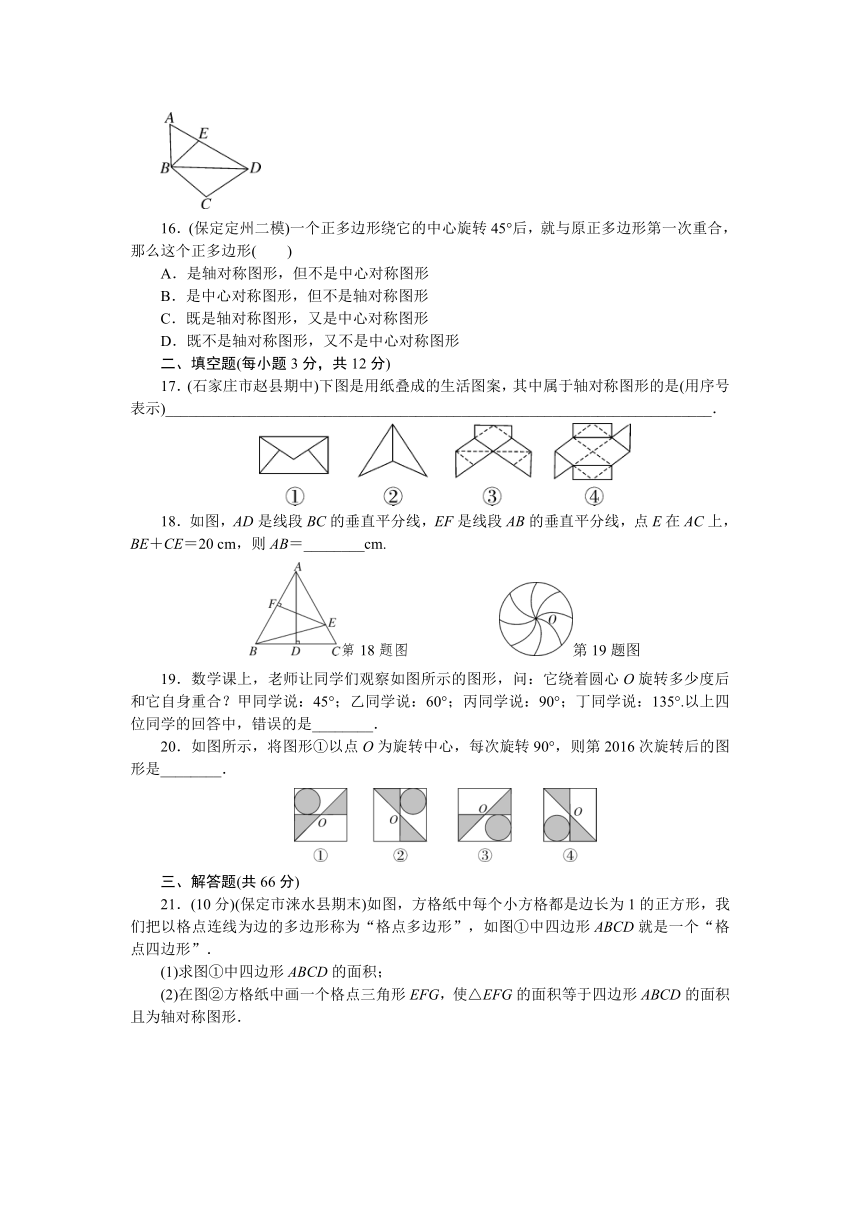
8.(河北省初中毕业生升学文化课考试说明)如图,直线l是一条河,P,Q两地相距8千米,P,Q两地到l的距离分别为2千米,5千米,欲在l上的某点M处修建一个水泵站,向P,Q两地供水.现有如下四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是( )
A.
B.
C.
D.
9.在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BC=16,且BD:DC=9:7,则点D到AB边的距离为( )
A.9
B.8
C.7
D.6
10.(邯郸涉县校级月考)已知△ABC中,AB=AC,AB的垂直平分线交AC于点D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
A.24cm和12cm
B.16cm和22cm
C.20cm和16cm
D.22cm和16cm
11.(保定市校级期中)把一个正方形三次对折后沿虚线剪下,如图所示,则所得的图形是( )
A.
B.
C.
D.
12.(湖州中考)如图,已知在△ABC中,CD是AB边上的高,BE平分∠ABC交CD于点E.若BC=5,DE=2,则△BCE的面积等于( )
A.10
B.7
C.5
D.4
第12题图 第13题图 第14题图
13.如图,已知AC平分∠PAQ,点M、N分别在边AP、AQ上,如果添加一个条件即可推出AM=AN,那么这个条件不可能是( )
A.MN⊥AC
B.MC=NC
C.∠ACM=∠ACN
D.∠AMC=∠ANC
14.如图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A.①
B.②
C.⑤
D.⑥
15.(河北模拟)如图,在四边形ABCD中,∠A=58°,∠C=100°,连接BD,E是AD上一点,连接BE,∠EBD=36°.若点A,C分别在线段BE,BD的垂直平分线上,则∠ADC的度数为( )
A.75°
B.65°
C.63°
D.61°
16.(保定定州二模)一个正多边形绕它的中心旋转45°后,就与原正多边形第一次重合,那么这个正多边形( )
A.是轴对称图形,但不是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,又不是中心对称图形
二、填空题(每小题3分,共12分)
17.(石家庄市赵县期中)下图是用纸叠成的生活图案,其中属于轴对称图形的是(用序号表示)________________________________________________________________________.
18.如图,AD是线段BC的垂直平分线,EF是线段AB的垂直平分线,点E在AC上,BE+CE=20
cm,则AB=________cm.
第18题图 第19题图
19.数学课上,老师让同学们观察如图所示的图形,问:它绕着圆心O旋转多少度后和它自身重合?甲同学说:45°;乙同学说:60°;丙同学说:90°;丁同学说:135°.以上四位同学的回答中,错误的是________.
20.如图所示,将图形①以点O为旋转中心,每次旋转90°,则第2016次旋转后的图形是________.
三、解答题(共66分)
21.(10分)(保定市涞水县期末)如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”,如图①中四边形ABCD就是一个“格点四边形”.
(1)求图①中四边形ABCD的面积;
(2)在图②方格纸中画一个格点三角形EFG,使△EFG的面积等于四边形ABCD的面积且为轴对称图形.
22.(10分)如图,公路OA和OB相交于点O,∠AOB内部有工厂C和D,现要修建一个货站P,使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置(不写作法,保留作图痕迹).
23.(10分)(秦皇岛海港区期末)如图,在△ABC中,边AC的垂直平分线DE与AC,AB分别交于点D和点E.
(1)作出边AC的垂直平分线DE;
(2)若△BCE的周长为10,AC=6,求△ABC的周长.
24.(11分)如图所示,∠BAC=∠ABD,AC=BD.点O是AD、BC的交点,点E是AB的中点,试判断OE和AB的位置关系,并给出证明.
25.(11分)如图,在△ABC中,点O是∠ABC、∠ACB平分线的交点,AB+BC+AC=12,过O作OD⊥BC于D点,且OD=2,求△ABC的面积.
26.(14分)如图,∠AOB=90°,OM平分∠AOB,将直角三角板的顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.
参考答案与解析
1.C 2.D 3.D 4.A 5.B
6.D 7.C 8.B 9.C 10.D
11.C 12.C 13.B 14.A
15.B 解析:∵点A、C分别在线段BE、BD的中垂线上,∴AE=AB,BC=DC.∵∠A=58°,∠C=100°,∴∠ABE==61°,∠CBD==40°.∵∠EBD=36°,∴∠ABC=∠ABE+∠EBD+∠CBD=61°+36°+40°=137°,∴∠ADC=360°-∠A-∠C-∠ABC=360°-58°-100°-137°=65°.故选B.
16.C 解析:∵一个正多边形绕它的中心旋转45°后,能与原多边形重合,∴360°÷45°=8,这个正多边形是正八边形,正八边形即是轴对称图形又是中心对称图形,故选C.
17.①②③ 18.20 19.乙 20.①
21.解:(1)根据面积公式得S=4×6-×2×1-×4×1-×3×4-×2×3=12;(5分)
(2)(只要画出一种即可).(10分)
22.解:图略.作∠AOB的平分线与CD的中垂线,其交点即是货站P的位置.(10分)
23.解:(1)如图;(4分)
(2)如图,连接CE,(5分)∵DE是AC的垂直平分线,∴AE=CE.∵△BCE的周长为10,∴BC+BE+CE=10,即BC+AB=10.(7分)∵AC=6,∴AB+BC+AC=16,∴△ABC的周长为16.(10分)
24.解:OE⊥AB.(2分)证明如下:在△BAC和△ABD中,∵∴△BAC≌△ABD,(6分)∴∠OBA=∠OAB,∴∠OAC=∠OBD.同理可证得△OAC≌△OBD,即OA=OB.又∵AE=BE,∠OAE=∠OBE,∴△OAE≌△OBE,(9分)∴∠OEA=∠OEB,∴∠OEA=×180°=90°,即OE⊥AB.(11分)
25.解:如图,作OE⊥AB于E,OF⊥AC于F,连接OA.(3分)∵点O是∠ABC、∠ACB平分线的交点,∴OE=OD,OF=OD,即OE=OF=OD=2,(5分)∴S△ABC=S△ABO+S△BCO+S△ACO=AB·OE+BC·OD+AC·OF=×2×(AB+BC+AC)=×2×12=12.(11分)
26.解:PC与PD相等.(3分)理由如下:过点P作PE⊥OA于点E,PF⊥OB于点F.(5分)∵OM平分∠AOB,∴PE=PF.∵∠PEO=∠EOF=∠PFO=90°,∴∠EPF=90°,∴∠EPC+∠CPF=90°.∵∠DPF+∠CPF=∠CPD=90°,∴∠EPC=∠FPD.(9分)在△PCE与△PDF中,∵∴△PCE≌△PDF,∴PC=PD.(14分)
时间:120分钟 满分:120分
班级:__________ 姓名:__________ 得分:__________
一、选择题(第1~10小题,每小题3分,第11~16小题每小题2分,共42分)
1.(保定市涞水县期末)涞水的文化底蕴深厚,涞水人民的生活健康向上.下面的四幅简笔画是从涞水的文化活动中抽象出来的,其中是轴对称图形的是( )
A.
B.
C.
D.
2.(大庆中考)以下图形中对称轴的数量小于3的是( )
3.(河北省初中毕业生升学文化课考试说明)如图,△ABC与△DEF关于直线l对称,则∠E的度数是( )
A.30°
B.50°
C.90°
D.100°
第3题图 第5题图
4.(衡水故城县校级月考)下列四幅图案在设计中用到平移变换方式的是( )
A.
B.
C.
D.
5.如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC中线的交点
B.△ABC三条角平分线的交点
C.△ABC三条高所在的直线交点
D.△ABC三边的中垂线的交点
6.(河北模拟)如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与A′是对应点
B.BO=B′O
C.AB∥A′B′
D.∠ABC=∠B′A′C′
第6题图 第7题图
7.如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于18cm,则AC的长等于( )
A.6cm
B.8cm
C.10cm
D.12cm
8.(河北省初中毕业生升学文化课考试说明)如图,直线l是一条河,P,Q两地相距8千米,P,Q两地到l的距离分别为2千米,5千米,欲在l上的某点M处修建一个水泵站,向P,Q两地供水.现有如下四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是( )
A.
B.
C.
D.
9.在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BC=16,且BD:DC=9:7,则点D到AB边的距离为( )
A.9
B.8
C.7
D.6
10.(邯郸涉县校级月考)已知△ABC中,AB=AC,AB的垂直平分线交AC于点D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
A.24cm和12cm
B.16cm和22cm
C.20cm和16cm
D.22cm和16cm
11.(保定市校级期中)把一个正方形三次对折后沿虚线剪下,如图所示,则所得的图形是( )
A.
B.
C.
D.
12.(湖州中考)如图,已知在△ABC中,CD是AB边上的高,BE平分∠ABC交CD于点E.若BC=5,DE=2,则△BCE的面积等于( )
A.10
B.7
C.5
D.4
第12题图 第13题图 第14题图
13.如图,已知AC平分∠PAQ,点M、N分别在边AP、AQ上,如果添加一个条件即可推出AM=AN,那么这个条件不可能是( )
A.MN⊥AC
B.MC=NC
C.∠ACM=∠ACN
D.∠AMC=∠ANC
14.如图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )
A.①
B.②
C.⑤
D.⑥
15.(河北模拟)如图,在四边形ABCD中,∠A=58°,∠C=100°,连接BD,E是AD上一点,连接BE,∠EBD=36°.若点A,C分别在线段BE,BD的垂直平分线上,则∠ADC的度数为( )
A.75°
B.65°
C.63°
D.61°
16.(保定定州二模)一个正多边形绕它的中心旋转45°后,就与原正多边形第一次重合,那么这个正多边形( )
A.是轴对称图形,但不是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,又不是中心对称图形
二、填空题(每小题3分,共12分)
17.(石家庄市赵县期中)下图是用纸叠成的生活图案,其中属于轴对称图形的是(用序号表示)________________________________________________________________________.
18.如图,AD是线段BC的垂直平分线,EF是线段AB的垂直平分线,点E在AC上,BE+CE=20
cm,则AB=________cm.
第18题图 第19题图
19.数学课上,老师让同学们观察如图所示的图形,问:它绕着圆心O旋转多少度后和它自身重合?甲同学说:45°;乙同学说:60°;丙同学说:90°;丁同学说:135°.以上四位同学的回答中,错误的是________.
20.如图所示,将图形①以点O为旋转中心,每次旋转90°,则第2016次旋转后的图形是________.
三、解答题(共66分)
21.(10分)(保定市涞水县期末)如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”,如图①中四边形ABCD就是一个“格点四边形”.
(1)求图①中四边形ABCD的面积;
(2)在图②方格纸中画一个格点三角形EFG,使△EFG的面积等于四边形ABCD的面积且为轴对称图形.
22.(10分)如图,公路OA和OB相交于点O,∠AOB内部有工厂C和D,现要修建一个货站P,使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置(不写作法,保留作图痕迹).
23.(10分)(秦皇岛海港区期末)如图,在△ABC中,边AC的垂直平分线DE与AC,AB分别交于点D和点E.
(1)作出边AC的垂直平分线DE;
(2)若△BCE的周长为10,AC=6,求△ABC的周长.
24.(11分)如图所示,∠BAC=∠ABD,AC=BD.点O是AD、BC的交点,点E是AB的中点,试判断OE和AB的位置关系,并给出证明.
25.(11分)如图,在△ABC中,点O是∠ABC、∠ACB平分线的交点,AB+BC+AC=12,过O作OD⊥BC于D点,且OD=2,求△ABC的面积.
26.(14分)如图,∠AOB=90°,OM平分∠AOB,将直角三角板的顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.
参考答案与解析
1.C 2.D 3.D 4.A 5.B
6.D 7.C 8.B 9.C 10.D
11.C 12.C 13.B 14.A
15.B 解析:∵点A、C分别在线段BE、BD的中垂线上,∴AE=AB,BC=DC.∵∠A=58°,∠C=100°,∴∠ABE==61°,∠CBD==40°.∵∠EBD=36°,∴∠ABC=∠ABE+∠EBD+∠CBD=61°+36°+40°=137°,∴∠ADC=360°-∠A-∠C-∠ABC=360°-58°-100°-137°=65°.故选B.
16.C 解析:∵一个正多边形绕它的中心旋转45°后,能与原多边形重合,∴360°÷45°=8,这个正多边形是正八边形,正八边形即是轴对称图形又是中心对称图形,故选C.
17.①②③ 18.20 19.乙 20.①
21.解:(1)根据面积公式得S=4×6-×2×1-×4×1-×3×4-×2×3=12;(5分)
(2)(只要画出一种即可).(10分)
22.解:图略.作∠AOB的平分线与CD的中垂线,其交点即是货站P的位置.(10分)
23.解:(1)如图;(4分)
(2)如图,连接CE,(5分)∵DE是AC的垂直平分线,∴AE=CE.∵△BCE的周长为10,∴BC+BE+CE=10,即BC+AB=10.(7分)∵AC=6,∴AB+BC+AC=16,∴△ABC的周长为16.(10分)
24.解:OE⊥AB.(2分)证明如下:在△BAC和△ABD中,∵∴△BAC≌△ABD,(6分)∴∠OBA=∠OAB,∴∠OAC=∠OBD.同理可证得△OAC≌△OBD,即OA=OB.又∵AE=BE,∠OAE=∠OBE,∴△OAE≌△OBE,(9分)∴∠OEA=∠OEB,∴∠OEA=×180°=90°,即OE⊥AB.(11分)
25.解:如图,作OE⊥AB于E,OF⊥AC于F,连接OA.(3分)∵点O是∠ABC、∠ACB平分线的交点,∴OE=OD,OF=OD,即OE=OF=OD=2,(5分)∴S△ABC=S△ABO+S△BCO+S△ACO=AB·OE+BC·OD+AC·OF=×2×(AB+BC+AC)=×2×12=12.(11分)
26.解:PC与PD相等.(3分)理由如下:过点P作PE⊥OA于点E,PF⊥OB于点F.(5分)∵OM平分∠AOB,∴PE=PF.∵∠PEO=∠EOF=∠PFO=90°,∴∠EPF=90°,∴∠EPC+∠CPF=90°.∵∠DPF+∠CPF=∠CPD=90°,∴∠EPC=∠FPD.(9分)在△PCE与△PDF中,∵∴△PCE≌△PDF,∴PC=PD.(14分)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
