2017年秋冀教版八年级数学上册第13章全等三角形 章末检测卷(含答案)
文档属性
| 名称 | 2017年秋冀教版八年级数学上册第13章全等三角形 章末检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 252.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-22 12:09:44 | ||
图片预览


文档简介
第十三章检测卷
时间:120分钟 满分:120分
班级:__________ 姓名:__________ 得分:__________
一、选择题(第1~10小题,每小题3分,第11~16小题,每小题2分,共42分)
1.如图,△ABC≌△ECD,AB和EC是对应边,C和D是对应点,则下列结论中错误的是( )
A.AB=CE
B.∠A=∠E
C.AC=DE
D.∠B=∠D
第1题图 第3题图
2.下列命题中,假命题是( )
A.同旁内角互补,两直线平行
B.如果a=b,则a2=b2
C.对应角相等的两个三角形全等
D.两边及夹角对应相等的两个三角形全等
3.(唐山市高邑县月考)如图,△ABC与△DEF是全等三角形,则图中相等的线段的组数是( )
A.3
B.4
C.5
D.6
4.(秦皇岛卢龙县期中)下列关于全等三角形的说法不正确的是( )
A.全等三角形的大小相等
B.两个等边三角形一定是全等三角形
C.全等三角形的形状相同
D.全等三角形的对应边相等
5.如图,点D在AB上,点E在AC上,且∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AE
B.∠AEB=∠ADC
C.BE=CD
D.AB=AC
6.(保定市涞水县期末)如图,给出下列四组条件:
①AB=DE,BC=EF,AC=DF;
②AB=DE,∠B=∠E,BC=EF;
③∠B=∠E,BC=EF,∠C=∠F;
④AB=DE,AC=DF,∠B=∠E.
其中,能使△ABC≌△DEF的条件共有( )
A.1组
B.2组
C.3组
D.4组
第6题图 第7题图
7.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段为( )
A.PO
B.PQ
C.MO
D.MQ
8.(石家庄市栾城县期中)已知线段a,b和m,求作△ABC,使BC=a,AC=b,BC边上的中线AD=m,作法合理的顺序依次为( )
①延长CD到B,使BD=CD;②连接AB;③作△ADC,使DC=a,AC=b,AD=m.
A.③①②
B.①②③
C.②③①
D.③②①
9.(孟津县期末)已知△ABC≌△DEF,若∠A=50°,∠C=30°,则∠E的度数为( )
A.30°
B.50°
C.60°
D.100°
10.(沧州市沧县月考)如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
11.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A.90°
B.150°
C.180°
D.210°
第11题图 第12题图
12.如图,OD=OC,BD=AC,∠O=70°,∠C=30°,则∠BED等于( )
A.45°
B.50°
C.55°
D.60°
13.(唐山迁安市期中)如图,在正方形ABCD中,BC=5,点E、F分别在AD,AB上,连接CE,CF.若AF=3,∠AFC=∠D+∠DCE,则△CDE的面积为( )
A.15
B.10
C.7.5
D.5
第13题图 第14题图
14.(宜昌中考)如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个
B.2个
C.3个
D.4个
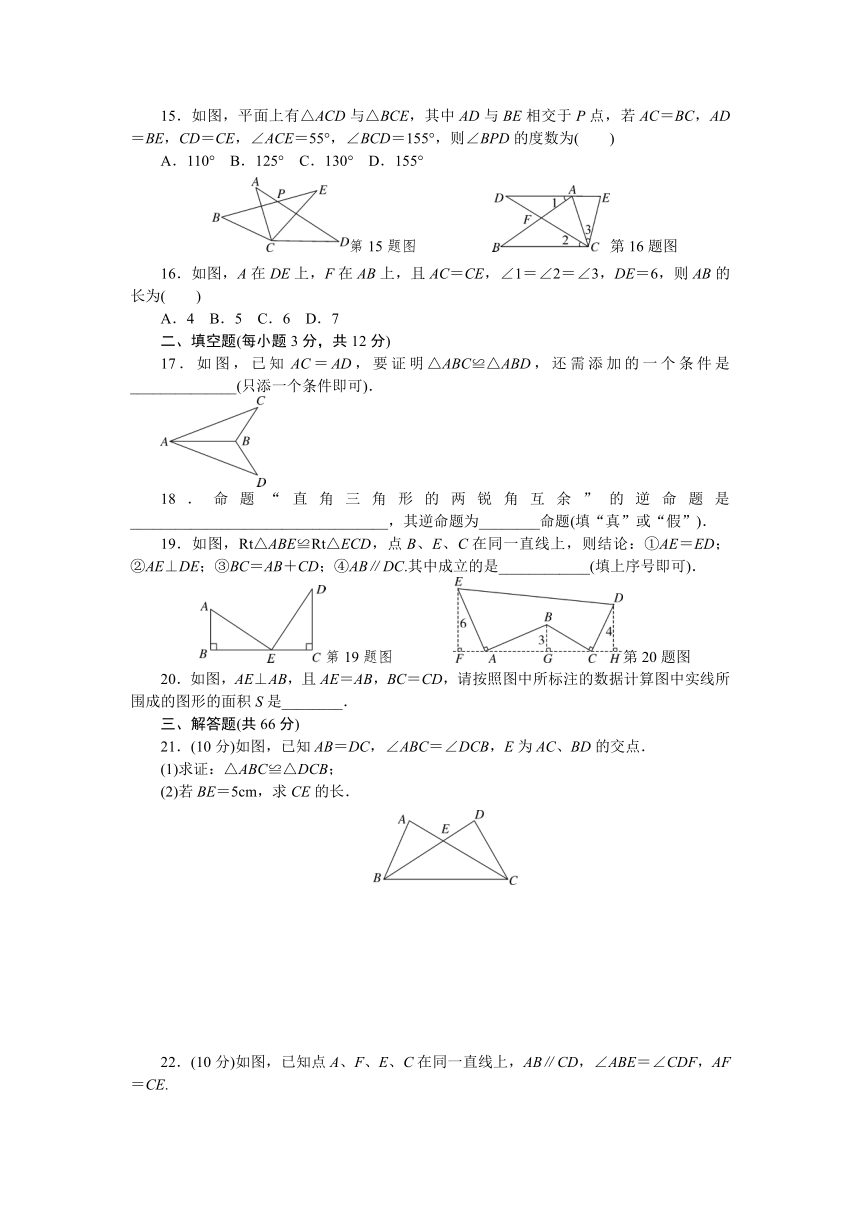
15.如图,平面上有△ACD与△BCE,其中AD与BE相交于P点,若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为( )
A.110°
B.125°
C.130°
D.155°
第15题图 第16题图
16.如图,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,DE=6,则AB的长为( )
A.4
B.5
C.6
D.7
二、填空题(每小题3分,共12分)
17.如图,已知AC=AD,要证明△ABC≌△ABD,还需添加的一个条件是______________(只添一个条件即可).
18.命题“直角三角形的两锐角互余”的逆命题是__________________________________,其逆命题为________命题(填“真”或“假”).
19.如图,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED;②AE⊥DE;③BC=AB+CD;④AB∥DC.其中成立的是____________(填上序号即可).
第19题图 第20题图
20.如图,AE⊥AB,且AE=AB,BC=CD,请按照图中所标注的数据计算图中实线所围成的图形的面积S是________.
三、解答题(共66分)
21.(10分)如图,已知AB=DC,∠ABC=∠DCB,E为AC、BD的交点.
(1)求证:△ABC≌△DCB;
(2)若BE=5cm,求CE的长.
22.(10分)如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.
23.(10分)如图,工人师傅要检查人字梁的∠B和∠C是否相等,但他手边没有量角器,只有一把刻度尺.他是这样操作的:①分别在BA和CA上取BE=CG;②在BC上取BD=CF;③量出DE的长为a米,FG的长为b米.如果a=b,则说明∠B和∠C是相等的.他的这种做法合理吗?为什么?
24.(11分)在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
题设:__________;结论:__________(均填写序号).
25.(11分)如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
26.(14分)问题背景:如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是________________;
探索延伸:如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立?并说明理由.
参考答案与解析
1.D 2.C 3.B 4.B 5.B 6.C 7.B 8.A
9.D 10.B 11.C 12.B 13.D 14.C
15.C 解析:在△ACD和△BCE中,∵AC=BC,CD=CE,AD=BE,∴△ACD≌△BCE(SSS),∴∠A=∠B,∠BCE=∠ACD,∴∠BCA=∠ECD.∵∠ACE=55°,∠BCD=155°,∴∠BCA+∠ECD=100°,∴∠BCA=∠ECD=50°.∵∠ACE=55°,∴∠ACD=105°,∴∠A+∠D=75°,∴∠B+∠D=75°.∵∠BCD=155°,∴∠BPD=360°-75°-155°=130°.故选C.
16.C 解析:∵∠2=∠3,∴∠2+∠DCA=∠3+∠DCA,∠DCE=∠BCA.∵∠1=∠2,∠AFD=∠BFC,∴∠CDE=∠ABC.在△ABC和△EDC中,∵∠ABC=∠EDC,∠ACB=∠ECD,AC=CE,∴△ABC≌△EDC,∴AB=DE=6.故选C.
17.BC=BD或∠CAB=∠DAB
18.两个锐角互余的三角形是直角三角形 真
19.①②③④ 20.50
21.(1)证明:在△ABC与△DCB中,AB=DC,∠ABC=∠DCB,BC=CB,∴△ABC≌△DCB(SAS);(4分)
(2)解:∵△ABC≌△DCB,∴∠A=∠D.在△ABE与△DCE中,∠A=∠D,∠AEB=∠DEC,AB=DC,∴△ABE≌△DCE(AAS),∴CE=BE=5
cm.(10分)
22.解:(1)△ABE≌△CDF,△ABC≌△CDA;(4分)
(2)证明△ABE≌△CDF.∵AB∥CD,∴∠BAC=∠DCA.∵AF=CE,∴AF+EF=CE+EF,∴AE=CF.在△ABE和△CDF中,∴△ABE≌△CDF(AAS).(10分)
23.解:这种做法合理.(4分)理由如下:∵BE=CG,BD=CF,a=b,∴△GFC≌△EDB(SSS),(8分)∴∠B=∠C.(10分)
24.解:答案不唯一,如:题设:①③④;结论:②.(4分)证明如下:在△ABC和△DEF中,∵AB=DE,∠B=∠E,∠1=∠2,∴△ABC≌△DEF(AAS),(8分)∴BC=EF,∴BC-FC=EF-FC,即BF=EC.(11分)
25.(1)证明:∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+CAD,即∠BAD=∠CAE.(3分)又∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS);(5分)
(2)解:BD⊥CE.(7分)证明如下:由(1)知△BAD≌△CAE,∴∠ADB=∠E.(9分)∵∠DAE=90°,∴∠E+∠ADE=90°,∴∠ADB+∠ADE=90°,即∠BDE=90°.∴BD⊥CE.(11分)
26.解:问题背景:EF=BE+DF;(3分)
探索延伸:EF=BE+DF仍然成立.(6分)
理由如下:延长FD到G,使DG=BE,连接AG,(8分)∵∠B+∠ADC=180°,∠ADC+∠ADG=180°,∴∠B=∠ADG.在△ABE和△ADG中,∵
∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG.(10分)∵∠EAF=∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF.在△AEF和△AGF中,∵∴△AEF≌△AGF(SAS),∴EF=GF.(12分)∵GF=DG+DF=BE+DF,∴EF=BE+DF.(14分)
时间:120分钟 满分:120分
班级:__________ 姓名:__________ 得分:__________
一、选择题(第1~10小题,每小题3分,第11~16小题,每小题2分,共42分)
1.如图,△ABC≌△ECD,AB和EC是对应边,C和D是对应点,则下列结论中错误的是( )
A.AB=CE
B.∠A=∠E
C.AC=DE
D.∠B=∠D
第1题图 第3题图
2.下列命题中,假命题是( )
A.同旁内角互补,两直线平行
B.如果a=b,则a2=b2
C.对应角相等的两个三角形全等
D.两边及夹角对应相等的两个三角形全等
3.(唐山市高邑县月考)如图,△ABC与△DEF是全等三角形,则图中相等的线段的组数是( )
A.3
B.4
C.5
D.6
4.(秦皇岛卢龙县期中)下列关于全等三角形的说法不正确的是( )
A.全等三角形的大小相等
B.两个等边三角形一定是全等三角形
C.全等三角形的形状相同
D.全等三角形的对应边相等
5.如图,点D在AB上,点E在AC上,且∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AE
B.∠AEB=∠ADC
C.BE=CD
D.AB=AC
6.(保定市涞水县期末)如图,给出下列四组条件:
①AB=DE,BC=EF,AC=DF;
②AB=DE,∠B=∠E,BC=EF;
③∠B=∠E,BC=EF,∠C=∠F;
④AB=DE,AC=DF,∠B=∠E.
其中,能使△ABC≌△DEF的条件共有( )
A.1组
B.2组
C.3组
D.4组
第6题图 第7题图
7.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段为( )
A.PO
B.PQ
C.MO
D.MQ
8.(石家庄市栾城县期中)已知线段a,b和m,求作△ABC,使BC=a,AC=b,BC边上的中线AD=m,作法合理的顺序依次为( )
①延长CD到B,使BD=CD;②连接AB;③作△ADC,使DC=a,AC=b,AD=m.
A.③①②
B.①②③
C.②③①
D.③②①
9.(孟津县期末)已知△ABC≌△DEF,若∠A=50°,∠C=30°,则∠E的度数为( )
A.30°
B.50°
C.60°
D.100°
10.(沧州市沧县月考)如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
11.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A.90°
B.150°
C.180°
D.210°
第11题图 第12题图
12.如图,OD=OC,BD=AC,∠O=70°,∠C=30°,则∠BED等于( )
A.45°
B.50°
C.55°
D.60°
13.(唐山迁安市期中)如图,在正方形ABCD中,BC=5,点E、F分别在AD,AB上,连接CE,CF.若AF=3,∠AFC=∠D+∠DCE,则△CDE的面积为( )
A.15
B.10
C.7.5
D.5
第13题图 第14题图
14.(宜昌中考)如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个
B.2个
C.3个
D.4个
15.如图,平面上有△ACD与△BCE,其中AD与BE相交于P点,若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为( )
A.110°
B.125°
C.130°
D.155°
第15题图 第16题图
16.如图,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,DE=6,则AB的长为( )
A.4
B.5
C.6
D.7
二、填空题(每小题3分,共12分)
17.如图,已知AC=AD,要证明△ABC≌△ABD,还需添加的一个条件是______________(只添一个条件即可).
18.命题“直角三角形的两锐角互余”的逆命题是__________________________________,其逆命题为________命题(填“真”或“假”).
19.如图,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED;②AE⊥DE;③BC=AB+CD;④AB∥DC.其中成立的是____________(填上序号即可).
第19题图 第20题图
20.如图,AE⊥AB,且AE=AB,BC=CD,请按照图中所标注的数据计算图中实线所围成的图形的面积S是________.
三、解答题(共66分)
21.(10分)如图,已知AB=DC,∠ABC=∠DCB,E为AC、BD的交点.
(1)求证:△ABC≌△DCB;
(2)若BE=5cm,求CE的长.
22.(10分)如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.
23.(10分)如图,工人师傅要检查人字梁的∠B和∠C是否相等,但他手边没有量角器,只有一把刻度尺.他是这样操作的:①分别在BA和CA上取BE=CG;②在BC上取BD=CF;③量出DE的长为a米,FG的长为b米.如果a=b,则说明∠B和∠C是相等的.他的这种做法合理吗?为什么?
24.(11分)在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
题设:__________;结论:__________(均填写序号).
25.(11分)如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
26.(14分)问题背景:如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是________________;
探索延伸:如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立?并说明理由.
参考答案与解析
1.D 2.C 3.B 4.B 5.B 6.C 7.B 8.A
9.D 10.B 11.C 12.B 13.D 14.C
15.C 解析:在△ACD和△BCE中,∵AC=BC,CD=CE,AD=BE,∴△ACD≌△BCE(SSS),∴∠A=∠B,∠BCE=∠ACD,∴∠BCA=∠ECD.∵∠ACE=55°,∠BCD=155°,∴∠BCA+∠ECD=100°,∴∠BCA=∠ECD=50°.∵∠ACE=55°,∴∠ACD=105°,∴∠A+∠D=75°,∴∠B+∠D=75°.∵∠BCD=155°,∴∠BPD=360°-75°-155°=130°.故选C.
16.C 解析:∵∠2=∠3,∴∠2+∠DCA=∠3+∠DCA,∠DCE=∠BCA.∵∠1=∠2,∠AFD=∠BFC,∴∠CDE=∠ABC.在△ABC和△EDC中,∵∠ABC=∠EDC,∠ACB=∠ECD,AC=CE,∴△ABC≌△EDC,∴AB=DE=6.故选C.
17.BC=BD或∠CAB=∠DAB
18.两个锐角互余的三角形是直角三角形 真
19.①②③④ 20.50
21.(1)证明:在△ABC与△DCB中,AB=DC,∠ABC=∠DCB,BC=CB,∴△ABC≌△DCB(SAS);(4分)
(2)解:∵△ABC≌△DCB,∴∠A=∠D.在△ABE与△DCE中,∠A=∠D,∠AEB=∠DEC,AB=DC,∴△ABE≌△DCE(AAS),∴CE=BE=5
cm.(10分)
22.解:(1)△ABE≌△CDF,△ABC≌△CDA;(4分)
(2)证明△ABE≌△CDF.∵AB∥CD,∴∠BAC=∠DCA.∵AF=CE,∴AF+EF=CE+EF,∴AE=CF.在△ABE和△CDF中,∴△ABE≌△CDF(AAS).(10分)
23.解:这种做法合理.(4分)理由如下:∵BE=CG,BD=CF,a=b,∴△GFC≌△EDB(SSS),(8分)∴∠B=∠C.(10分)
24.解:答案不唯一,如:题设:①③④;结论:②.(4分)证明如下:在△ABC和△DEF中,∵AB=DE,∠B=∠E,∠1=∠2,∴△ABC≌△DEF(AAS),(8分)∴BC=EF,∴BC-FC=EF-FC,即BF=EC.(11分)
25.(1)证明:∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+CAD,即∠BAD=∠CAE.(3分)又∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS);(5分)
(2)解:BD⊥CE.(7分)证明如下:由(1)知△BAD≌△CAE,∴∠ADB=∠E.(9分)∵∠DAE=90°,∴∠E+∠ADE=90°,∴∠ADB+∠ADE=90°,即∠BDE=90°.∴BD⊥CE.(11分)
26.解:问题背景:EF=BE+DF;(3分)
探索延伸:EF=BE+DF仍然成立.(6分)
理由如下:延长FD到G,使DG=BE,连接AG,(8分)∵∠B+∠ADC=180°,∠ADC+∠ADG=180°,∴∠B=∠ADG.在△ABE和△ADG中,∵
∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG.(10分)∵∠EAF=∠BAD,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF.在△AEF和△AGF中,∵∴△AEF≌△AGF(SAS),∴EF=GF.(12分)∵GF=DG+DF=BE+DF,∴EF=BE+DF.(14分)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
