2017年秋湘教版七年级数学上册章末检测卷-第4章 图形的认识
文档属性
| 名称 | 2017年秋湘教版七年级数学上册章末检测卷-第4章 图形的认识 |

|
|
| 格式 | zip | ||
| 文件大小 | 451.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-22 13:20:39 | ||
图片预览

文档简介
第4章检测卷
时间:100分钟 满分:120分
题号
一
二
三
总分
得分
一、选择题(每小题3分,共30分)
1.下图中的几何体是棱柱的是( )
2.下列几何语言表述中,一定正确的是( )
A.过A,B,C三点作直线
B.作直线AB,CD相交于点m
C.延长射线AB
D.在射线AB上截取线段AC
3.如图,田亮同学用剪刀沿虚线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
A.垂线段最短
B.经过一点有无数条直线
C.经过两点,有且仅有一条直线
D.两点之间线段最短
4.在下面几何体中,从上面看得到三角形的是( )
5.下列不能用一副三角板画出的角是( )
A.15°
B.75°
C.105°
D.125°
6.如图,直线AB和CD相交于O点,∠EOB=90°,则图中∠1与∠2的关系是( )
A.∠1与∠2互补
B.∠1与∠2互余
C.∠1与∠2相等
D.∠1=2∠2
7.延长线段AB至C,使BC=AB,D为AC的中点,且CD=3cm,则AB的长是( )
A.3.2cm
B.3.4cm
C.3.5cm
D.3.6cm
8.已知∠AOB=30°,由∠AOB的顶点O引射线OC,若∠AOC∶∠AOB=4∶3,那么∠BOC=( )
A.10°
B.40°
C.70°
D.10°或70°
9.两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A.2cm
B.4cm
C.2cm或22cm
D.4cm或44cm
10.由梅州到广州的某一车次的列车,运行途中停靠的车站依次是梅州——兴宁——华城——河源——惠州——东莞——广州,那么要为该车次列车制作的火车票有( )
A.6种
B.12种
C.21种
D.42种
二、填空题(每小题3分,共24分)
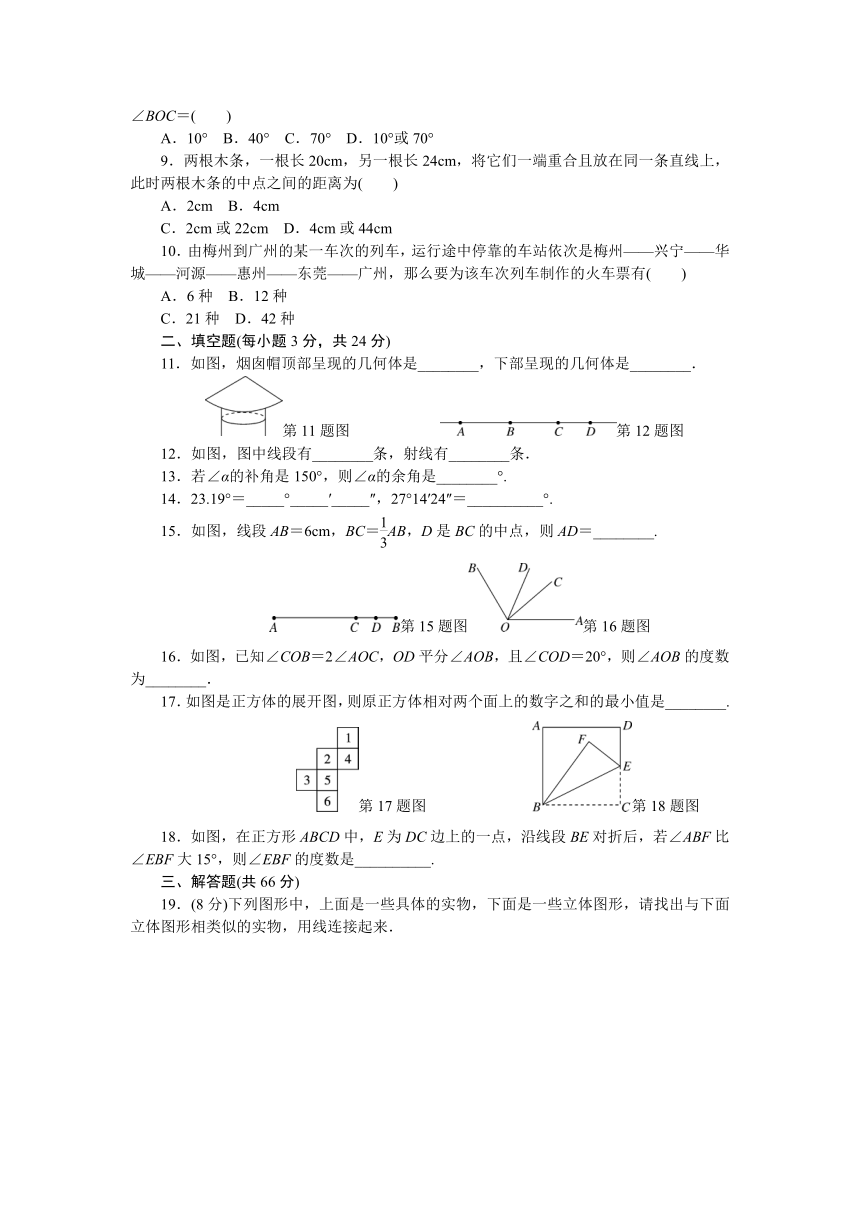
11.如图,烟囱帽顶部呈现的几何体是________,下部呈现的几何体是________.
第11题图 第12题图
12.如图,图中线段有________条,射线有________条.
13.若∠α的补角是150°,则∠α的余角是________°.
14.23.19°=_____°_____′_____″,27°14′24″=__________°.
15.如图,线段AB=6cm,BC=AB,D是BC的中点,则AD=________.
第15题图第16题图
16.如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB的度数为________.
17.如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是________.
第17题图 第18题图
18.如图,在正方形ABCD中,E为DC边上的一点,沿线段BE对折后,若∠ABF比∠EBF大15°,则∠EBF的度数是__________.
三、解答题(共66分)
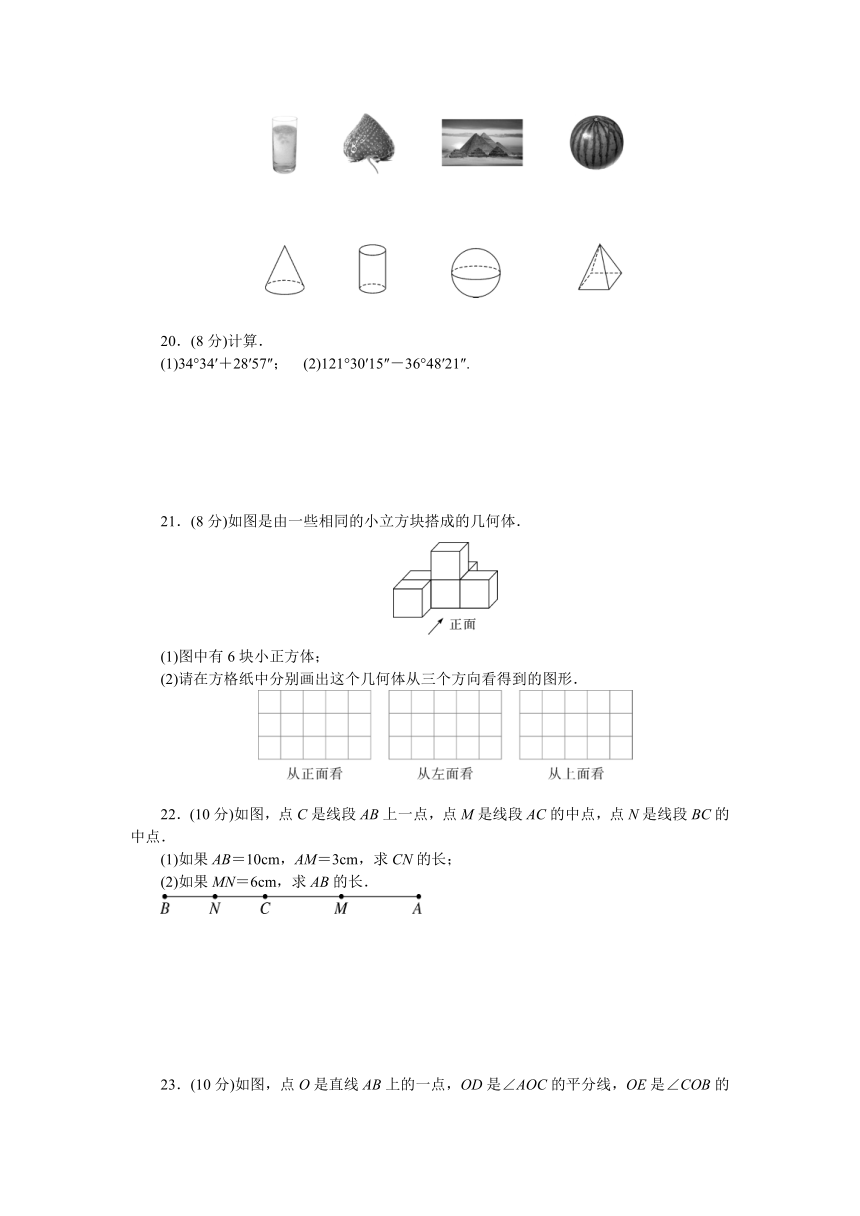
19.(8分)下列图形中,上面是一些具体的实物,下面是一些立体图形,请找出与下面立体图形相类似的实物,用线连接起来.
20.(8分)计算.
(1)34°34′+28′57″;
(2)121°30′15″-36°48′21″.
21.(8分)如图是由一些相同的小立方块搭成的几何体.
(1)图中有6块小正方体;
(2)请在方格纸中分别画出这个几何体从三个方向看得到的图形.
22.(10分)如图,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点.
(1)如果AB=10cm,AM=3cm,求CN的长;
(2)如果MN=6cm,求AB的长.
23.(10分)如图,点O是直线AB上的一点,OD是∠AOC的平分线,OE是∠COB的平分线,若∠AOD=14°,求∠DOE,∠BOE的度数.
24.(10分)如图,已知点C是线段AB的中点,AB=9,若E是直线AB上一点,且BE=2.
(1)请依题意补全图形;
(2)求CE的长.
25.(12分)定义:从一个角的顶点出发,把这个角分成1∶2的两个角的射线,叫作这个角的三分线,显然,一个角的三分线有两条.
(1)如图①,已知OC是∠AOB的一条三分线,且∠BOC>∠AOC,若∠AOB=75°,求∠AOC的度数;
(2)如图②,已知∠AOB=90°,若OC,OD是∠AOB的两条三分线.
①求∠COD的度数;
②在①的基础上,现以O为中心,将∠COD顺时针旋转n°得到∠C′OD′.当OA恰好是∠C′OD′的三分线时,求n的值.
参考答案与解析
1.D 2.D 3.D 4.D 5.D
6.B 7.D 8.D 9.C 10.D
11.圆锥 圆柱 12.6 8
13.60 14.23 11 24 27.24
15.5cm 16.120° 17.6 18.25°
19.解:如图所示.(8分)
20.解:(1)原式=35°2′57″.(4分)(2)原式=84°41′54″.(8分)
21.解:(1)6(2分)
(2)如图所示.(每图2分)
22.解:(1)因为点M是线段AC的中点,AM=3cm,所以AC=2AM=6cm.(2分)因为AB=10cm,所以BC=AB-AC=4cm.(3分)又因为N是BC的中点,所以CN=BC=2cm.(5分)
(2)因为MN=NC+CM=BC+AC=(AC+BC)=AB,(8分)又因为MN=6cm,所以AB=12cm.(10分)
23.解:因为OD是∠AOC的平分线,∠AOD=14°,则∠AOC=2∠AOD=2×14°=28°.(2分)因为∠AOB=180°,OE是∠COB的平分线,所以∠BOE=∠BOC=×(180°-∠AOC)=76°.(7分)∠DOE=∠BOC+∠AOC=76°+14°=90°.(10分)
24.解:(1)如图所示.满足题意的有以下两种情况.(4分)
(2)由(1)知有两种情形:①当E在线段AB上,如图①.因为C是AB的中点,AB=9,所以BC=AC=×9=4.5.因为BE=2,所以CE=BC-BE=4.5-2=2.5;(7分)②当E在线段AB的延长线上,如图②.由①可知BC=4.5,所以CE=BC+BE=4.5+2=6.5.(9分)综上所述,CE的长为2.5或6.5.(10分)
25.解:(1)因为OC是∠AOB的一条三分线,且∠BOC>∠AOC,所以∠AOC=∠AOB=25°.(3分)
(2)①因为∠AOB=90°,OC,OD是∠AOB的两条三分线,所以∠COD=∠AOB=30°.(6分)
②分两种情况:如图③,当OA是∠C′OD′的三分线,且∠AOD′>∠AOC′时,∠AOC′=10°,所以∠DOC′=30°-10°=20°,所以∠DOD′=20°+30°=50°;(9分)如图④,当OA是∠C′OD′的三分线,且∠AOD′<∠AOC′时,∠AOC′=20°,所以∠DOC′=30°-20°=10°,所以∠DOD′=10°+30°=40°.(11分)综上所述,n=40或50.(12分)
时间:100分钟 满分:120分
题号
一
二
三
总分
得分
一、选择题(每小题3分,共30分)
1.下图中的几何体是棱柱的是( )
2.下列几何语言表述中,一定正确的是( )
A.过A,B,C三点作直线
B.作直线AB,CD相交于点m
C.延长射线AB
D.在射线AB上截取线段AC
3.如图,田亮同学用剪刀沿虚线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
A.垂线段最短
B.经过一点有无数条直线
C.经过两点,有且仅有一条直线
D.两点之间线段最短
4.在下面几何体中,从上面看得到三角形的是( )
5.下列不能用一副三角板画出的角是( )
A.15°
B.75°
C.105°
D.125°
6.如图,直线AB和CD相交于O点,∠EOB=90°,则图中∠1与∠2的关系是( )
A.∠1与∠2互补
B.∠1与∠2互余
C.∠1与∠2相等
D.∠1=2∠2
7.延长线段AB至C,使BC=AB,D为AC的中点,且CD=3cm,则AB的长是( )
A.3.2cm
B.3.4cm
C.3.5cm
D.3.6cm
8.已知∠AOB=30°,由∠AOB的顶点O引射线OC,若∠AOC∶∠AOB=4∶3,那么∠BOC=( )
A.10°
B.40°
C.70°
D.10°或70°
9.两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A.2cm
B.4cm
C.2cm或22cm
D.4cm或44cm
10.由梅州到广州的某一车次的列车,运行途中停靠的车站依次是梅州——兴宁——华城——河源——惠州——东莞——广州,那么要为该车次列车制作的火车票有( )
A.6种
B.12种
C.21种
D.42种
二、填空题(每小题3分,共24分)
11.如图,烟囱帽顶部呈现的几何体是________,下部呈现的几何体是________.
第11题图 第12题图
12.如图,图中线段有________条,射线有________条.
13.若∠α的补角是150°,则∠α的余角是________°.
14.23.19°=_____°_____′_____″,27°14′24″=__________°.
15.如图,线段AB=6cm,BC=AB,D是BC的中点,则AD=________.
第15题图第16题图
16.如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB的度数为________.
17.如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是________.
第17题图 第18题图
18.如图,在正方形ABCD中,E为DC边上的一点,沿线段BE对折后,若∠ABF比∠EBF大15°,则∠EBF的度数是__________.
三、解答题(共66分)
19.(8分)下列图形中,上面是一些具体的实物,下面是一些立体图形,请找出与下面立体图形相类似的实物,用线连接起来.
20.(8分)计算.
(1)34°34′+28′57″;
(2)121°30′15″-36°48′21″.
21.(8分)如图是由一些相同的小立方块搭成的几何体.
(1)图中有6块小正方体;
(2)请在方格纸中分别画出这个几何体从三个方向看得到的图形.
22.(10分)如图,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点.
(1)如果AB=10cm,AM=3cm,求CN的长;
(2)如果MN=6cm,求AB的长.
23.(10分)如图,点O是直线AB上的一点,OD是∠AOC的平分线,OE是∠COB的平分线,若∠AOD=14°,求∠DOE,∠BOE的度数.
24.(10分)如图,已知点C是线段AB的中点,AB=9,若E是直线AB上一点,且BE=2.
(1)请依题意补全图形;
(2)求CE的长.
25.(12分)定义:从一个角的顶点出发,把这个角分成1∶2的两个角的射线,叫作这个角的三分线,显然,一个角的三分线有两条.
(1)如图①,已知OC是∠AOB的一条三分线,且∠BOC>∠AOC,若∠AOB=75°,求∠AOC的度数;
(2)如图②,已知∠AOB=90°,若OC,OD是∠AOB的两条三分线.
①求∠COD的度数;
②在①的基础上,现以O为中心,将∠COD顺时针旋转n°得到∠C′OD′.当OA恰好是∠C′OD′的三分线时,求n的值.
参考答案与解析
1.D 2.D 3.D 4.D 5.D
6.B 7.D 8.D 9.C 10.D
11.圆锥 圆柱 12.6 8
13.60 14.23 11 24 27.24
15.5cm 16.120° 17.6 18.25°
19.解:如图所示.(8分)
20.解:(1)原式=35°2′57″.(4分)(2)原式=84°41′54″.(8分)
21.解:(1)6(2分)
(2)如图所示.(每图2分)
22.解:(1)因为点M是线段AC的中点,AM=3cm,所以AC=2AM=6cm.(2分)因为AB=10cm,所以BC=AB-AC=4cm.(3分)又因为N是BC的中点,所以CN=BC=2cm.(5分)
(2)因为MN=NC+CM=BC+AC=(AC+BC)=AB,(8分)又因为MN=6cm,所以AB=12cm.(10分)
23.解:因为OD是∠AOC的平分线,∠AOD=14°,则∠AOC=2∠AOD=2×14°=28°.(2分)因为∠AOB=180°,OE是∠COB的平分线,所以∠BOE=∠BOC=×(180°-∠AOC)=76°.(7分)∠DOE=∠BOC+∠AOC=76°+14°=90°.(10分)
24.解:(1)如图所示.满足题意的有以下两种情况.(4分)
(2)由(1)知有两种情形:①当E在线段AB上,如图①.因为C是AB的中点,AB=9,所以BC=AC=×9=4.5.因为BE=2,所以CE=BC-BE=4.5-2=2.5;(7分)②当E在线段AB的延长线上,如图②.由①可知BC=4.5,所以CE=BC+BE=4.5+2=6.5.(9分)综上所述,CE的长为2.5或6.5.(10分)
25.解:(1)因为OC是∠AOB的一条三分线,且∠BOC>∠AOC,所以∠AOC=∠AOB=25°.(3分)
(2)①因为∠AOB=90°,OC,OD是∠AOB的两条三分线,所以∠COD=∠AOB=30°.(6分)
②分两种情况:如图③,当OA是∠C′OD′的三分线,且∠AOD′>∠AOC′时,∠AOC′=10°,所以∠DOC′=30°-10°=20°,所以∠DOD′=20°+30°=50°;(9分)如图④,当OA是∠C′OD′的三分线,且∠AOD′<∠AOC′时,∠AOC′=20°,所以∠DOC′=30°-20°=10°,所以∠DOD′=10°+30°=40°.(11分)综上所述,n=40或50.(12分)
同课章节目录
