2017秋华师大版七年级数学上册 第4章 图形的初步认识专训试题
文档属性
| 名称 | 2017秋华师大版七年级数学上册 第4章 图形的初步认识专训试题 |  | |
| 格式 | zip | ||
| 文件大小 | 467.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-26 16:51:57 | ||
图片预览




文档简介
专训一:常见立体图形的分类
立体图形就是各部分不都在同一平面内的几何图形,常见的立体图形有柱体(圆柱、棱柱)、锥体(圆锥、棱锥)、台体(圆台、棱台)(以后将学)和球体(球)四类.
INCLUDEPICTURE
"../../../训练角度1.tif"
\
MERGEFORMAT
按柱、锥、球分类
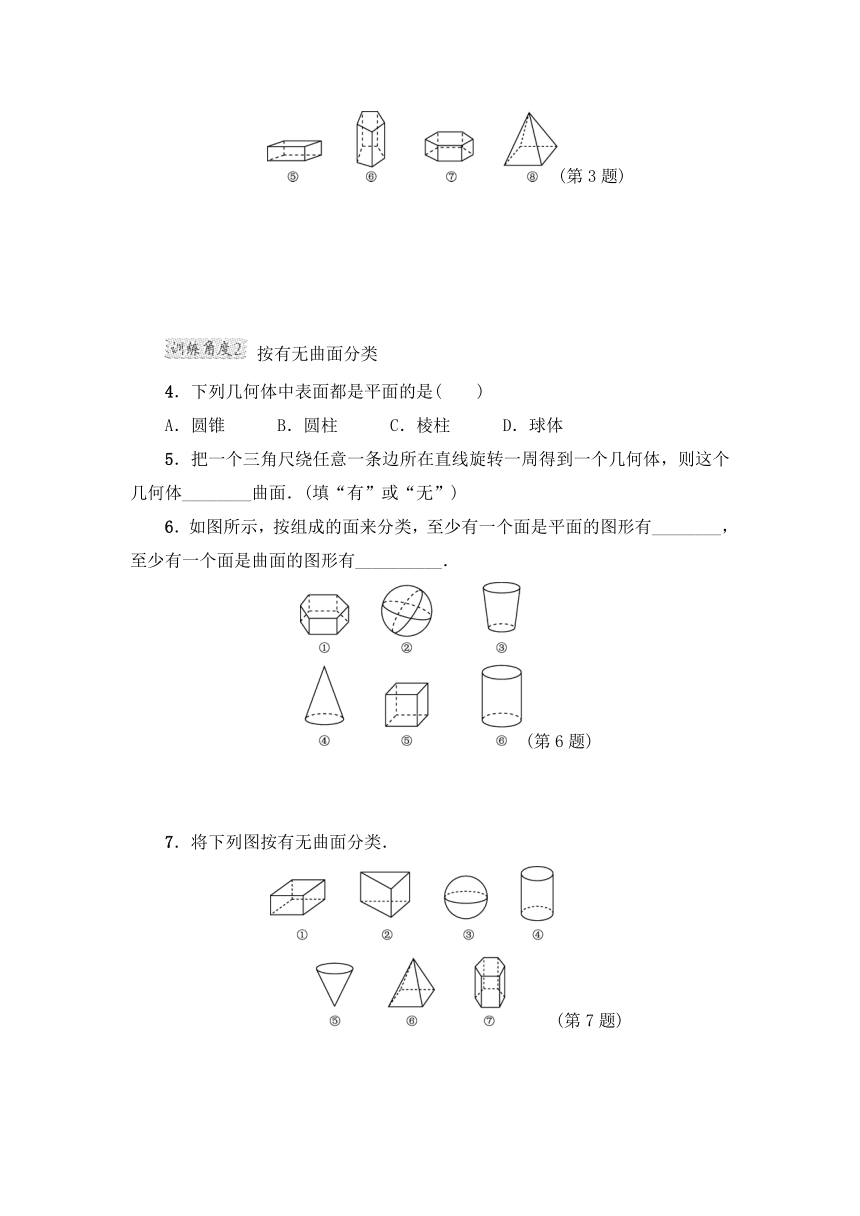
1.如图所示,都为柱体的是( )
A
B
C
D
2.在如图所示的图形中,是圆柱的有________,是棱柱的有________.(填序号)
(第2题)
3.(1)把图中的立体图形按特征分类,并说明分类标准;
(2)图中③与⑥各有什么特征?有哪些相同点和不同点?
(第3题)
INCLUDEPICTURE
"../../../训练角度2.tif"
\
MERGEFORMAT
按有无曲面分类
4.下列几何体中表面都是平面的是( )
A.圆锥 B.圆柱 C.棱柱 D.球体
5.把一个三角尺绕任意一条边所在直线旋转一周得到一个几何体,则这个几何体________曲面.(填“有”或“无”)
6.如图所示,按组成的面来分类,至少有一个面是平面的图形有________,至少有一个面是曲面的图形有__________.
(第6题)
7.将下列图按有无曲面分类.
(第7题)
专训二:立体图形的展开与折叠
一个立体图形的平面展开图的形状由展开的方式决定,不同的展开方式得到的平面展开图是不一样的,但无论怎样展开,平面展开图都应体现出原立体图形面的个数与形状.
INCLUDEPICTURE
"../../../训练角度1.tif"
\
MERGEFORMAT
正方体的展开图
1.(中考·德州)如图给定的是纸盒的外表面,下面能由它折叠而成的是( )
(第1题)
2.如图所示的图形都是由6个大小一样的正方形拼成的,哪些是正方体的平面展开图?
(第2题)
INCLUDEPICTURE
"../../../训练角度2.tif"
\
MERGEFORMAT
长方体的展开图
3.如图是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题.
(1)如果面A是长方体的上面,那么哪一面会在下面?
(2)如果面F是长方体的后面,从左面看是面B,那么哪一面会在上面?
(3)从右面看是面A,从上面看是面E,那么哪一面会在前面?
(第3题)
INCLUDEPICTURE
"../../../训练角度3.tif"
\
MERGEFORMAT
其他立体图形的展开图
4.如图是一些几何体的平面展开图,请写出这些几何体的名称.
(第4题)
INCLUDEPICTURE
"../../../训练角度4.tif"
\
MERGEFORMAT
立体图形展开图的相关计算问题
5.(中考·青岛)如图所示,下列几何体是由棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),则第n个几何体中,只有两个面涂色的小立方体共有________个.
(第5题)
6.如图所示形状的铁皮能围成一个长方体铁桶吗?如果能,它的体积有多大?
(第6题)
专训三:巧用线段中点的有关计算
利用线段的中点可以得到线段相等或有倍数关系的等式来辅助计算,由相等的线段去判断中点时,点必须在线段上才能成立.
INCLUDEPICTURE
"../../../训练角度1.tif"
\
MERGEFORMAT
线段中点问题
类型1 与线段中点有关的计算
1.已知A,B,C三点在同一条直线上,若线段AB=20
cm,线段BC=8
cm,M,N分别是线段AB,BC的中点.
(1)求线段MN的长;
(2)根据(1)中的计算过程和结果,设AB=a,BC=b,且a>b,其他条件都不变,你能猜出MN的长度吗?(直接写出结果)
类型2 与线段中点有关的说明题
2.画线段MN=3
cm,在线段MN上取一点Q,使MQ=NQ;延长线段MN到点A,使AN=MN;延长线段NM到点B,使BM=BN.
(1)求线段BM的长;
(2)求线段AN的长;
(3)试说明点Q是哪些线段的中点.
INCLUDEPICTURE
"../../../训练角度2.tif"
\
MERGEFORMAT
线段分点问题
类型1 与线段分点有关的计算(设参法)
3.如图,B,C两点把线段AD分成2∶4∶3三部分,M是AD的中点,CD=6
cm,求线段MC的长.
(第3题)
类型2 线段分点与方程的结合
4.A,B两点在数轴上的位置如图,O为原点,现A,B两点分别以1个单位长度/秒,4个单位长度/秒的速度同时向左运动.
(1)几秒后,原点恰好在两点正中间?
(2)几秒后,恰好有OA∶OB=1∶2
(第4题)
专训四:线段上的动点问题
解决线段上的动点问题一般需注意:(1)找准点的各种可能的位置;(2)通常可用设元法,表示出移动变化后的线段的长(有可能是常数,那就是定值),再由题意列方程求解.
INCLUDEPICTURE
"../../../训练角度1.tif"
\
MERGEFORMAT
线段上动点与中点问题的综合
1.(1)如图①,D是线段AB上任意一点,M,N分别是AD,DB的中点,若AB=16,求MN的长;
(2)如图②,AB=16,点D是线段AB上一动点,M,N分别是AD,DB的中点,能否求出线段MN的长?若能,求出其长,若不能,试说明理由;
(3)如图③,AB=16,点D运动到线段AB的延长线上,其他条件不变,能否求出线段MN的长?若能,求出其长,若不能,试说明理由.
(4)你能用一句简洁的话,描述你发现的结论吗?
(第1题)
INCLUDEPICTURE
"../../../训练角度2.tif"
\
MERGEFORMAT
线段上动点问题中的存在性问题
2.如图,已知数轴上两点A,B对应的数分别为-2、6,O为原点,点P为数轴上的一动点,其对应的数为x.
(第2题)
(1)PA=________;PB=________(用含x的式子表示);
(2)在数轴上是否存在点P,使PA+PB=10?若存在,请求出x的值;若不存在,请说明理由.
(3)点P以1个单位长度/s的速度从点O向右运动,同时点A以5个单位长度/s的速度向左运动,点B以20个单位长度/s的速度向右运动,在运动过程中,M,N分别是AP,OB的中点,问:的值是否发生变化?请说明理由.
INCLUDEPICTURE
"../../../训练角度3.tif"
\
MERGEFORMAT
线段和差倍分关系中的动点问题
3.如图,线段AB=24,动点P从A出发,以每秒2个单位长度的速度沿射线AB运动,M为AP的中点.
(1)出发多少秒后,PB=2AM
(2)当P在线段AB上运动时,试说明2BM-BP为定值.
(3)当P在线段AB的延长线上运动时,N为BP的中点,下列两个结论:①MN长度不变;②MA+PN的值不变.选出正确的结论,并求出其值.
(第3题)
专训五:巧用角平分线的有关计算
角平分线的定义是进行角度计算常见的重要依据,因此解这类题要从角平分线找角的数量关系,利用图形中相等的角的位置关系,结合角的和、差关系求解.
INCLUDEPICTURE
"../../../训练角度1.tif"
\
MERGEFORMAT
角平分线间的夹角问题(分类讨论思想)
1.已知∠AOB=100°,∠BOC=60°,OM平分∠AOB,ON平分∠BOC,求∠MON的度数.
INCLUDEPICTURE
"../../../训练角度2.tif"
\
MERGEFORMAT
巧用角平分线解决折叠问题(折叠法)
2.如图,将一张长方形纸斜折过去,使顶点A落在A′处,BC为折痕,然后把BE折过去,使之落在A′B所在直线上,折痕为BD,那么两折痕BC与BD间的夹角是多少度?
(第2题)
INCLUDEPICTURE
"../../../训练角度3.tif"
\
MERGEFORMAT
巧用角平分线解决角的和、差、倍、分问
题(方程思想)
3.如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=19°,求∠AOB的度数.
(第3题)
INCLUDEPICTURE
"../../../训练角度4.tif"
\
MERGEFORMAT
巧用角平分线解决角的推理问题
(转化思想)
4.如图,已知OD,OE,OF分别为∠AOB,∠AOC,∠BOC的平分线,∠DOE和∠COF有怎样的关系?说明理由.
(第4题)
INCLUDEPICTURE
"../../../训练角度5.tif"
\
MERGEFORMAT
角平分线与线段中点的结合
5.如图,(1)已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数.
(3)如果(1)中∠BOC=β(β<90°),其他条件不变,求∠MON的度数.
(4)从(1)(2)(3)的结果中能得到什么样的规律?
(5)线段的计算与角的计算存在着紧密的联系,它们之间可以互相借鉴解法,请你模仿(1)~(4),设计一道以线段为背景的计算题,给出解答,并写出其中的规律.
(第5题)
专训六:巧解时针与分针的夹角问题
时钟时针、分针转动角度的问题,要注意时针转动一大格,转过角度为周角的十二分之一,即30°.每一个大格之间又分为5个小格,每个小格的角度是6°.注意时针与分针转动角度的速度比是1∶12,时针转动30°,分针转动360°.分针与秒针转动角度的速度之比是1∶60,分针转动6°(一个小格),秒针转动360°.
INCLUDEPICTURE
"../../../训练角度1.tif"
\
MERGEFORMAT
利用时间求角度
类型1 按固定时间求角度
1.(1)从上午11时到下午1时30分,这期间时针转过了________;下午1:30,时针、分针的夹角是________.
(2)3点20分时,时针与分针的夹角是多少度?
类型2 按动态时间求角度
2.小华是个数学迷,最近他在研究钟面角(时针与分针组成的角)问题,他想和大家一起来讨论相关问题.
(1)分针每分钟转6度,时针每分钟转________度;
(2)你能指出下面各个图中时针与分针之间夹角的大小吗?图①的钟面角为________度,图②的钟面角为________度.
(第2题)
(3)12:00时,时针和分针重合,至少经过多长时间会再次出现时针和分针重合的现象?此时,时针和分针各转动了多少度?
INCLUDEPICTURE
"../../../训练角度2.tif"
\
MERGEFORMAT
利用角度求时间(方程思想)
3.如图,观察时钟,解答下列问题.
(1)在2时和3时之间什么时刻,时针和分针的夹角为直角?
(第3题)
(2)小明下午五点多有事外出时,看到墙上钟面的时针和分针的夹角为90°,下午不到六点回家时,发现时针与分针的夹角又为90°,那么小明外出了多长时间?
专训一:线段或角的计数问题
1.几何计数问题应用广泛,解决方法是“有序数数法”,数数时要做到不重复、不遗漏.
2.解决这类问题要用到分类讨论思想及从特殊到一般的思想.
3.回顾前面线段、直线的计数公式,比较这些计数公式的区别与联系.
INCLUDEPICTURE
"../../../训练角度1.tif"
\
MERGEFORMAT
线段条数的计数问题
1.先阅读文字,再解答问题.
(第1题)
如图,在一条直线上取两点,可以得到1条线段,在一条直线上取三点可得到3条线段,其中以A1为端点的向右的线段有2条,以A2为端点的向右的线段有1条,所以共有2+1=3(条).
(1)在一条直线上取四个点,以A1为端点的向右的线段有______条,以A2为端点的向右的线段有_________________________________________________________________条,
以A3为端点的向右的线段有______条,共有______+______+______=______(条).
(2)在一条直线上取五个点,以A1为端点的向右的线段有______条,以A2为端点的向右的线段有________条,以A3为端点的向右的线段有________条,以A4为端点的向右的线段有______条,共有______+______+______+______=____(条).
(3)在一条直线上取n个点(n≥2),共有________条线段.
(4)某学校七年级共有6个班进行辩论赛,规定进行单循环赛(每两个班赛一场),那么该校七年级的辩论赛共要进行多少场?
(5)乘火车从A站出发,沿途经过5个车站方可到达B站,那么A,B两站之间最多有多少种不同的票价?需要安排多少种不同的车票?
INCLUDEPICTURE
"../../../训练角度2.tif"
\
MERGEFORMAT
平面内直线相交所得交点与平面的计数问题
2.为了探究同一平面内的几条直线相交最多能产生多少个交点,能把平面最多分成几部分,我们从最简单的情形入手,如图所示.
(第2题)
列表如下:
直线条数
最多交点个数
平面最多分成部分数
1
0
2
2
1
4
3
3
7
…
…
…
(1)当直线条数为5时,最多有________个交点,可写成和的形式为__________;把平面最多分成________部分,可写成和的形式为__________;
(2)当直线条数为10时,最多有________个交点,把平面最多分成________部分;
(3)当直线条数为n时,最多有多少个交点?把平面最多分成多少部分?
INCLUDEPICTURE
"../../../训练角度3.tif"
\
MERGEFORMAT
关于角的个数的计数问题
3.有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点,如图,如果过∠BAC的顶点A:
(1)在角的内部作一条射线,那么图中一共有几个角?
(2)在角的内部作两条射线,那么图中一共有几个角?
(3)在角的内部作三条射线,那么图中一共有几个角?
(4)在角的内部作n条射线,那么图中一共有几个角?
(第3题)
专训二:分类思想在线段和角的计算中的应用
解答有关点和线的位置关系、线段条数或长度、角的个数或大小等问题时,由于题目中没有给出具体的图形,而根据题意又可能出现多种情况,就应不重不漏地分情况加以讨论,这种思想称为分类讨论思想.需要进行分类讨论的题目,综合性一般较强.
INCLUDEPICTURE
"../../../应用1.tif"
\
MERGEFORMAT
分类思想在线段的计算中的应用
1.已知线段AB=12,在线段AB上有C,D,M,N四点,且AC∶CD∶DB=1∶2∶3,AM=AC,DN=DB,求线段MN的长.
2.如图,点O为原点,点A对应的数为1,点B对应的数为-3.
(1)若点P在数轴上,且PA+PB=6,求P对应的数;
(2)若点M在数轴上,且MA∶MB=1∶3,求M对应的数;
(3)若点A的速度为5个单位长度/秒,点B的速度为2个单位长度/秒,点O的速度为1个单位长度/秒,A,B,O同时向右运动,几秒后,点O恰为线段AB的中点?
(第2题)
INCLUDEPICTURE
"../../../应用2.tif"
\
MERGEFORMAT
分类思想在角的计算中的应用
3.如图,已知∠AOC=2∠BOC,∠AOC的余角比∠BOC小30°.
(1)求∠AOB的度数;
(2)过点O作射线OD,使得∠AOC=4∠AOD,请你求出∠COD的度数.
(第3题)
4.已知OM和ON分别平分∠AOC和∠BOC.
(1)如图,若OC在∠AOB的内部时,探究∠MON与∠AOB的数量关系;
(2)若OC在∠AOB的外部,且OC不与OA,OB重合时,请你画出图形,并探究∠MON与∠AOB的数量关系.(提示:分三种情况讨论)
(第4题)
专训三:几种常见的热门考点
本章知识从大的方面可分为两部分,第一部分是立体几何的初步认识,第二部分是平面图形的认识,这些都是几何学习的基础.本章主要考查立体图形的识别、立体图形的三视图,图形的展开与折叠,直线、射线、线段及角的有关计算.立体图形的平面展开图,三视图等是中考中常见考点,通常以选择、填空形式呈现.
INCLUDEPICTURE
"../../../热门考点1.tif"
\
MERGEFORMAT
立体图形的识别
1.在①球体;②柱体;③圆锥;④棱柱;⑤棱锥中,必是多面体(指由四个或四个以上多边形所围成的立体图形)的是( )
A.①②③④⑤
B.②和③
C.④
D.④和⑤
2.如图所示的立体图形中,是柱体的是________.(填序号)
(第2题)
INCLUDEPICTURE
"../../../热门考点2.tif"
\
MERGEFORMAT
立体图形的三视图
3.(2015·泰安)下列四个几何体(如图):
(第3题)
其中左视图与俯视图相同的几何体共有( )个.
A.1 B.2 C.3 D.4
4.一个几何体的三视图如图所示,则这个几何体是( )
A.四棱锥
B.四棱柱
C.三棱锥
D.三棱柱
(第4题)
(第5题)
5.由一些完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则组成这个几何体的小正方体的个数可能是__________.
INCLUDEPICTURE
"../../../热门考点3.tif"
\
MERGEFORMAT
图形的展开与折叠
6.小亮为今年参加中考的好友小杰制作了一个正方体礼品盒(如图),六个面上各有一个字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的表面展开图可能是( )
eq
\a\vs4\al(,,,) eq
\a\vs4\al()
(第6题)
7.如图是一个长方体形状包装盒的表面展开图.折叠制作完成后得到长方体的容积是(包装材料厚度不计)( )
(第7题)
A.40×40×70
B.70×70×80
C.80×80×80
D.40×70×80
INCLUDEPICTURE
"../../../热门考点4.tif"
\
MERGEFORMAT
直线、射线、线段
8.下列关于作图的语句中正确的是( )
A.画直线AB=10厘米
B.画射线OB=10厘米
C.已知A,B,C三点,过这三点画一条直线
D.过直线AB外一点画一条直线和直线AB相交
9.如图,已知线段AB,在BA的延长线上取一点C,使CA=3AB,则线段CA与线段CB的长度之比为( )
(第9题)
A.3∶4
B.2∶3
C.3∶5
D.1∶2
10.开学整理教室时,老师总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌摆在一条线上,整整齐齐,这是因为________________________.
11.乘火车从A站出发,沿途经过3个车站方可到达B站,那么A,B两站之间需要安排________种不同的车票.
12.如图,已知AB和CD的公共部分BD=AB=CD,线段AB,CD的中点E,F之间的距离是10
cm,求AB,CD的长.
(第12题)
INCLUDEPICTURE
"../../../热门考点5.tif"
\
MERGEFORMAT
角及角的有关计算
13.有下列说法:
①两条射线所组成的图形叫做角;
②一条射线旋转而成的图形叫做角;
③两边成一条直线的角是平角;
④平角是一条直线.
其中正确的个数是( )
A.1
B.2
C.3
D.4
14.4点10分,时针与分针所夹的小于平角的角为( )
A.55°
B.65°
C.70°
D.以上结论都不对
15.如图所示,两块三角板的直角顶点O重合在一起,且OB恰好平分∠COD,则∠AOD的度数是________度.
(第15题)
16.若一个角的余角比它的补角的少20°,则这个角的度数为________.
17.如图,O是直线AB上一点,OC,OD是从O点引出的两条射线,OE平分∠AOC,∠BOC∶∠AOE∶∠AOD=2∶5∶8,求∠BOD的度数.
(第17题)
INCLUDEPICTURE
"../../../热门考点6.tif"
\
MERGEFORMAT
数学思想方法的应用
a.数形结合思想
18.往返于A,B两个城市的客车,中途有三个停靠站,分别为C,D,E.
(1)最多共有多少种不同的票价?
(2)要准备多少种车票?
b.方程思想
19.互为补角的两个角的度数之比是5∶4,求这两个角的度数.
c.分类讨论思想
20.已知同一平面内四点,过其中任意两点画直线,仅能画4条,则这四个点的位置关系是( )
A.任意三点不在同一条直线上
B.四点在同一条直线上
C.最多三点在同一条直线上
D.三点在同一条直线上,第四点在这条直线外
21.已知一条射线OA,若从点O再引两条射线OB和OC,使∠AOB=80°,∠BOC=40°,若OD平分∠AOC,则∠BOD等于________.
d.转化思想
22.如图所示,一观测塔的底座部分是四棱柱,现要从下底面A点修建钢筋扶梯,经过点M,N到点D′(M在BB′上,N在CC′上),再进入顶部的观测室,已知AB=BC=CD,试确定使扶梯的总长度最小的点M,N的位置.
(第22题)
答案
专训一
1.C
2.④ ①③⑥
3.解:(1)按柱体、锥体、球体分:①③⑤⑥⑦为柱体;④⑧为锥体;②为球体.(分类标准不唯一)
(2)③是圆柱,圆柱的上、下底面都是圆,侧面是一个曲面;⑥是五棱柱,上、下底面是形状、大小相同的五边形,侧面是5个长方形,侧面的个数与底面边数相等.
相同点:两者都有两个底面,且两个底面的形状,大小相同.
不同点:圆柱的底面是圆,五棱柱的底面是五边形.圆柱的侧面是一个曲面,五棱柱的侧面由5个长方形组成.
4.C 5.有
6.①③④⑤⑥ ②③④⑥
7.解:有曲面的是③④⑤;无曲面的是①②⑥⑦.
专训二
1.B
2.解:题图①②③④⑥都是正方体的平面展开图.
3.解:(1)如果面A是长方体的上面,那么面C会在下面.
(2)如果面F是长方体的后面,从左面看是面B,那么向外折时面C会在上面,向里折时面A会在上面.
(3)从右面看是面A,从上面看是面E,那么向外折时从前面看是面B,向里折时从前面看是面D.
4.解:①三棱锥;②四棱锥;③五棱锥;④三棱柱;⑤圆柱;⑥圆锥.
点拨:棱锥和棱柱的共同点是棱锥、棱柱都是以底面多边形的边数来命名的,如三棱锥是指底面为三角形的棱锥,而五棱柱是指底面为五边形的棱柱.它们的不同点是棱柱的侧棱互相平行,而棱锥的侧棱交于一点.
5.(8n-4) 点拨:从下往上数两个面涂色的小立方体个数,图①中:第一层4个,第二层0个;图②中:第一层4个;第二层4个,第三层4个;图③中,第一层4个,第二层4个,第三层4个,第四层8个,故第n个几何体中涂两个面的小立方体有[4n+4(n-1)]个,即(8n-4)个.
6.解:能围成,体积为40×70×65=182
000(cm3).
答:体积为182
000
cm3.
阶段强化专题训练
专训三
1.解:(1)分两种情况:①当点C在线段AB上时,如图①,因为M为AB的中点,所以MB=AB=×20=10(cm).因为N为BC的中点,所以BN=BC=×8=4(cm),所以MN=MB-BN=10-4=6(cm);
(第1题)
②当点C在线段AB的延长线上时,如图②,因为M为AB的中点,所以MB=AB=×20=10(cm).因为N为BC的中点,所以BN=BC=×8=4(cm),所以MN=MB+BN=10+4=14(cm).
(2)MN=(a+b)或MN=(a-b).
2.解:如图.
(第2题)
(1)因为BM=BN,所以BM=MN.
因为MN=3
cm,所以BM=×3=1.5(cm).
(2)因为AN=MN,MN=3
cm.所以AN=1.5
cm.
(3)MN=3
cm,MQ=NQ,所以MQ=NQ=1.5
cm.
所以BQ=BM+MQ=1.5+1.5=3(cm),
AQ=AN+NQ=3
cm.所以BQ=QA.
所以Q是线段MN的中点,也是线段AB的中点.
3.解:设AB=2k
cm,则BC=4k
cm,CD=3k
cm,AD=2k+4k+3k=9k(cm).因为CD=6
cm,即3k=6,所以k=2,则AD=18
cm.又因为M是AD的中点,所以MD=AD=×18=9(cm).所以MC=MD-CD=9-6=3(cm).
4.解:(1)设运动时间为x秒,依题意得x+3=12-4x,解得x=1.8.
答:1.8秒后,原点恰好在两点正中间.
(2)设运动时间为t秒.
①B与A相遇前:12-4t=2(t+3),即t=1;
②B与A相遇后:4t-12=2(t+3),即t=9.
答:1秒或9秒后,恰好有OA∶OB=1∶2.
专训四
1.解:(1)MN=DM+DN=AD+BD=(AD+BD)=AB=8.
(2)能.MN=DM+DN=AD+BD=(AD+BD)=AB=8.
(3)能.MN=MD-DN=AD-BD=(AD-BD)=AB=8.
(4)MN的长始终等于AB长的一半.
2.解:(1)|x+2| |x-6|
(2)分三种情况:
①当点P在A,B之间时,PA+PB=8,故舍去;
②当点P在B点右边时,PA=x+2,PB=x-6,因为(x+2)+(x-6)=10,所以x=7;
③当点P在A点左边时,PA=-x-2,PB=6-x,因为(-x-2)+(6-x)=10,所以x=-3.
所以当x=-3或7时,PA+PB=10,
(3)的值不发生变化,理由如下:
设运动时间为t
s.
则OP=t,OA=5t+2,OB=20t+6,AB=OA+OB=25t+8,AB-OP=24t+8,AP=OA+OP=6t+2,AM=AP=3t+1,OM=OA-AM=5t+2-(3t+1)=2t+1,ON=OB=10t+3,所以MN=OM+ON=12t+4,所以==2,即的值不发生变化.
3.解:(1)设出发x秒后,PB=2AM,则PA=2x,PB=24-2x,AM=x,所以24-2x=2x,即x=6.
(2)设运动时间为t秒,则BM=24-t,PB=24-2t,所以2BM-BP=2(24-t)-(24-2t)=24,即2BM-BP为定值.
(3)因为PA=2t,AM=PM=t,PB=2t-24,PN=PB=t-12,
所以①MN=PM-PN=t-(t-12)=12.
所以MN长度不变,为定值;
②MA+PN=t+t-12=2t-12,
所以MA+PN的值是变化的.
综上所述,正确的结论是①,且MN=12.
专训五
1.解:分两种情况:(1)如图①,当OC落在∠AOB的内部时,
因为OM平分∠AOB,ON平分∠BOC,
所以∠BOM=∠AOB=×100°=50°,∠BON=∠BOC=×60°=30°,
所以∠MON=∠BOM-∠BON=50°-30°=20°.
(第1题)
(2)如图②,当OC落在∠AOB的外部时,
因为OM平分∠AOB,ON平分∠BOC,
所以∠BOM=∠AOB=×100°=50°,∠BON=∠BOC=×60°=30°.
所以∠MON=∠BOM+∠BON=50°+30°=80°.
综上可知,∠MON的度数为20°或80°.
点拨:本题已知中没有图,作图时应考虑OC落在∠AOB的内部和外部两种情况,体现了分类讨论思想的运用.
2.解:因为∠CBA与∠CBA′折叠重合,所以∠CBA=∠CBA′.
因为∠EBD与∠A′BD折叠重合,
所以∠EBD=∠A′BD.
又因为这四个角的和是180°,
所以∠CBD=∠CBA′+∠A′BD=×180°=90°.
即两折痕BC与BD间的夹角为90°.
点拨:本题可运用折叠法动手折叠,便于寻找角与角之间的关系.
3.解:设∠AOC=x,则∠COB=2x.
因为OD平分∠AOB,所以∠AOD=∠AOB=(∠AOC+∠BOC)=x.
又因为∠DOC=∠AOD-∠AOC,所以19°=x-x,
解得x=38°.所以∠AOB=3x=3×38°=114°.
点拨:根据图形巧设未知数用角与角之间的数量关系构建关于未知数的方程求出角的度数体现了方程思想的运用.
4.解:∠DOE=∠COF.理由如下:
因为OD平分∠AOB,所以∠DOB=∠AOB.
因为OF平分∠BOC,所以∠BOF=∠BOC,所以∠DOB+∠BOF=∠AOB+∠BOC=∠AOC,即∠DOF=∠AOC.又因为OE平分∠AOC,所以∠EOC=∠AOC,所以∠DOF=∠EOC.又因为∠DOF=∠DOE+∠EOF,∠EOC=∠EOF+∠COF,所以∠DOE=∠COF.
点拨:欲找出∠DOE与∠COF的关系只要找到∠DOF与∠COE的关系即可.而OD,OF分别是∠AOB,∠BOC的平分线,那么由此可得到∠DOF与∠AOC的关系,而且又有∠AOC=2∠COE,即可转化成∠DOF与∠COE的关系,进而可得到∠DOE与∠COF的关系,体现了转化思想的运用.
5.解:(1)因为OM平分∠AOC,ON平分∠BOC,
所以∠MOC=∠AOC,∠NOC=∠BOC,
所以∠MON=∠MOC-∠NOC=∠AOC-∠BOC=(∠AOB+∠BOC)-∠BOC=∠AOB=45°.
(2)∠MON=∠AOB=.
(3)∠MON=∠AOB=45°.
(4)从(1)(2)(3)的结果中可看出:∠MON的大小总等于∠AOB大小的一半,而与∠BOC的大小变化无关.
(5)可设计的问题为:如图,线段AB=a,延长AB到C使BC=b,点M,N分别是线段AC,BC的中点,求线段MN的长.
(第5题)
解:因为点M,N分别是线段AC,BC的中点,
所以MC=AC,NC=BC.
所以MN=MC-NC=(AC-BC)=AB=a.
规律:线段MN的长度总等于线段AB长度的一半,而与线段BC的长度变化无关.
专训六
1.解:(1)75° 135°
(2)时针每小时转30°,分针每分钟转6°.时针从指向12开始转过的角度为3×30°=100°,分针从指向12开始转过的角度为20×6°=120°,120°-100°=20°,即3点20分时,时针与分针的夹角是20°.
2.解:(1)0.5 (2)30 22.5
(3)设至少x分钟后分针与时针再次重合,则6x-0.5x=360,解得x=,
即至少经过分钟会再次出现时针与分针重合的现象.
×0.5°=° ×6°=°
答:时针转了°,分针转了°.
3.解:(1)设从2时经过x分,分针与时针的夹角为直角,依题意,有×6°=90°,解得x=.
答:在2时分时,时针和分针的夹角为直角.
(2)设小明外出了y分钟,则时针走了0.5y度,分针走了6y度.
根据题意,列方程为6y=90+0.5y+90,解得y=.
答:小明外出了分钟.
点拨:在钟表问题中,常利用时针与分针的转动度数关系:分针每分转动6°,时针每分转动0.5°,并且结合起点时时针和分针的位置关系建立角的数量关系.
全章整合提升密码
专训一
1.解:(1)3 2 1 3 2 1 6 (2)4 3 2 1 4 3 2 1 10
(3)
(4)七年级有6个班,类似于一条直线上有6个点,每两个班赛一场,类似于两点之间有一条线段,那么七年级的辩论赛共要进行=15(场).
(5)从A站出发,沿途经过5个车站到达B站,类似于一条直线上有7个点,此时共有线段=21(条),即A,B两站之间最多有21种不同的票价.因为来往两站的车票起点与终点不同,所以A,B两站之间需要安排21×2=42(种)不同的车票.
2.解:(1)10 1+2+3+4 16 1+1+2+3+4+5
(2)45 56
(3)当直线条数为n时,
最多有1+2+3+…+(n-1)=(个)交点;
把平面最多分成1+1+2+3+…+n=部分.
3.解:(1)如题图①,已知∠BAC,如果在其内部作一条射线,显然这条射线就会和∠BAC的两条边都组成一个角,这样一共就有1+2=3(个)角.
(2)题图①中有1+2=3(个)角,如果再在题图①的角的内部增加一条射线,即为题图②,显然这条射线就会和图中的其他三条射线再组成三个角,即题图②中共有1+2+3=6(个)角.
(3)如题图③,在角的内部作三条射线,即在题图②中再增加一条射线,同样这条射线就会和图中的其他四条射线再组成四个角,即题图③中共有1+2+3+4=10(个)角.
(4)综上所述,如果在一个角的内部作n条射线,则图中共有1+2+3+…+n+(n+1)=(个)角.
专训二
1.解:因为AB=12,AC∶CD∶DB=1∶2∶3,
所以AC=AB=12×=2,CD=AB=12×=4,DB=AB=12×=6.
因为AM=AC,DN=DB,
所以MC=AC=2×=1,DN=DB=6×=.
①当点N在点D右侧时,如图①,
MN=MC+CD+DN=1+4+=;
(第1题)
②当点N在点D左侧时,如图②,
MN=MC+CD-DN=1+4-=.
综上所述,线段MN的长为或.
点拨:首先要根据题意,画出图形.由于点N的位置不确定,故要考虑分类讨论.
2.解:(1)①当点P在A,B之间时,不合题意,舍去;
②当点P在A点右边时,点P对应的数为2;
③当点P在B点左边时,点P对应的数为-4.
(2)①当M在线段AB上时,M对应的数为0;
②当M在线段BA的延长线上时,M对应的数为3;
③当M在线段AB的延长线上时,不合题意,舍去.
(3)设运动x秒时,点B运动到点B′,点A运动到点A′,点O运动到点O′,此时O′A′=O′B′,点A′,B′在点O′两侧,则BB′=2x,OO′=x,AA′=5x,
所以点B′对应的数为2x-3,点O′对应的数为x,点A′对应的数为5x+1,
因为O′A′=5x+1-x=4x+1,O′B′=x-(2x-3)=3-x,所以
4x+1=3-x,解得x=0.4.
即0.4秒后,点O恰为线段AB的中点.
3.解:(1)设∠BOC=x,则∠AOC=2x,
由题意得90°-2x+30°=x,解得x=40°.
因为∠AOC=2∠BOC,所以∠AOB=∠BOC=40°.
(2)情况一:当OD在∠AOC内部时,如图①,
由(1)得∠AOC=80°.
因为∠AOC=4∠AOD,所以∠AOD=20°,
所以∠COD=∠AOC-∠AOD=80°-20°=60°.
(第3题)
情况二:当OD在∠AOC外部时,如图②,
由(1)得∠AOC=80°.
因为∠AOC=4∠AOD,所以∠AOD=20°,
所以∠COD=∠AOD+∠AOC=20°+80°=100°.
综上所述,∠COD的度数为60°或100°.
4.解:(1)因为OM和ON分别平分∠AOC和∠BOC,
所以∠MOC=∠AOC,∠NOC=∠BOC.
所以∠MON=∠MOC+∠NOC=∠AOC+∠BOC=(∠AOC+∠BOC)=∠AOB.
(2)情况一:如图①,
因为OM和ON分别平分∠AOC和∠BOC,
所以∠MOC=∠AOC=(∠AOB+∠BOC),∠NOB=∠BOC.
所以∠MON=∠MOB+∠NOB=∠MOC-∠BOC+∠BOC=∠MOC-∠BOC=(∠AOB+∠BOC)-∠BOC=∠AOB.
(第4题)
情况二:如图②,
因为OM和ON分别平分∠AOC和∠BOC,
所以∠AOM=∠AOC,∠NOC=∠BOC=(∠AOB+∠AOC)=∠AOB+∠AOC.
所以∠MON=∠AOM+∠AON=∠AOC+(∠NOC-∠AOC)=∠NOC-∠AOC=∠AOB+∠AOC-∠AOC=∠AOB.
情况三,如图③,
因为OM和ON分别平分∠AOC和∠BOC,
所以∠MOC=∠AOC,∠NOC=∠BOC.
所以∠MON=∠MOC+∠NOC=∠AOC+∠BOC=(∠AOC+∠BOC)=(360°-∠AOB)=180°-∠AOB.
综上所述,∠MON与∠AOB的数量关系是∠MON=∠AOB或∠MON=180°-∠AOB.
专训三
1.D 2.②③ 3.D 4.B 5.4或5或6或7 6.C 7.D 8.D
9.A 10.两点确定一条直线
11.20
12.解:因为BD=AB=CD,所以CD=AB.
因为F是CD的中点,
所以DF=CD=×AB=AB.
因为E是AB的中点,所以EB=AB,
所以ED=EB-DB=AB-AB=AB.
所以EF=ED+DF=AB+AB=AB=10
cm,
所以AB=12
cm,所以CD=AB=16
cm.
13.A 14.B 15.135 16.40°
17.解:设∠BOC=2x°,则∠AOE=5x°,∠AOD=8x°.
因为O是直线AB上一点,所以∠AOB=180°,
所以∠COE=(180-7x)°.
因为OE平分∠AOC,所以∠AOE=∠COE,
即5x=180-7x,解得x=15,
所以∠AOD=8×15°=120°,所以∠BOD=60°.
18.解:(1)根据题意画出示意图,如图所示,线段有AC,AD,AE,AB,CD,CE,CB,DE,DB,EB,共10条,因此最多共有10种不同的票价.
(2)同一路段,往返时起点和终点正好相反,所以要准备20种车票.
(第18题)
19.解:设这两个角分别为5x°,4x°.
因为这两个角互补,所以5x+4x=180,解得x=20.
5x=100,4x=80,
所以这两个角分别为100°,80°.
20.D 21.60°或20°
22.解:画出四棱柱的侧面展开图,点M,N的位置如图①所示,则M,N在四棱柱上的位置如图②所示.
(第22题)
立体图形就是各部分不都在同一平面内的几何图形,常见的立体图形有柱体(圆柱、棱柱)、锥体(圆锥、棱锥)、台体(圆台、棱台)(以后将学)和球体(球)四类.
INCLUDEPICTURE
"../../../训练角度1.tif"
\
MERGEFORMAT
按柱、锥、球分类
1.如图所示,都为柱体的是( )
A
B
C
D
2.在如图所示的图形中,是圆柱的有________,是棱柱的有________.(填序号)
(第2题)
3.(1)把图中的立体图形按特征分类,并说明分类标准;
(2)图中③与⑥各有什么特征?有哪些相同点和不同点?
(第3题)
INCLUDEPICTURE
"../../../训练角度2.tif"
\
MERGEFORMAT
按有无曲面分类
4.下列几何体中表面都是平面的是( )
A.圆锥 B.圆柱 C.棱柱 D.球体
5.把一个三角尺绕任意一条边所在直线旋转一周得到一个几何体,则这个几何体________曲面.(填“有”或“无”)
6.如图所示,按组成的面来分类,至少有一个面是平面的图形有________,至少有一个面是曲面的图形有__________.
(第6题)
7.将下列图按有无曲面分类.
(第7题)
专训二:立体图形的展开与折叠
一个立体图形的平面展开图的形状由展开的方式决定,不同的展开方式得到的平面展开图是不一样的,但无论怎样展开,平面展开图都应体现出原立体图形面的个数与形状.
INCLUDEPICTURE
"../../../训练角度1.tif"
\
MERGEFORMAT
正方体的展开图
1.(中考·德州)如图给定的是纸盒的外表面,下面能由它折叠而成的是( )
(第1题)
2.如图所示的图形都是由6个大小一样的正方形拼成的,哪些是正方体的平面展开图?
(第2题)
INCLUDEPICTURE
"../../../训练角度2.tif"
\
MERGEFORMAT
长方体的展开图
3.如图是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题.
(1)如果面A是长方体的上面,那么哪一面会在下面?
(2)如果面F是长方体的后面,从左面看是面B,那么哪一面会在上面?
(3)从右面看是面A,从上面看是面E,那么哪一面会在前面?
(第3题)
INCLUDEPICTURE
"../../../训练角度3.tif"
\
MERGEFORMAT
其他立体图形的展开图
4.如图是一些几何体的平面展开图,请写出这些几何体的名称.
(第4题)
INCLUDEPICTURE
"../../../训练角度4.tif"
\
MERGEFORMAT
立体图形展开图的相关计算问题
5.(中考·青岛)如图所示,下列几何体是由棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),则第n个几何体中,只有两个面涂色的小立方体共有________个.
(第5题)
6.如图所示形状的铁皮能围成一个长方体铁桶吗?如果能,它的体积有多大?
(第6题)
专训三:巧用线段中点的有关计算
利用线段的中点可以得到线段相等或有倍数关系的等式来辅助计算,由相等的线段去判断中点时,点必须在线段上才能成立.
INCLUDEPICTURE
"../../../训练角度1.tif"
\
MERGEFORMAT
线段中点问题
类型1 与线段中点有关的计算
1.已知A,B,C三点在同一条直线上,若线段AB=20
cm,线段BC=8
cm,M,N分别是线段AB,BC的中点.
(1)求线段MN的长;
(2)根据(1)中的计算过程和结果,设AB=a,BC=b,且a>b,其他条件都不变,你能猜出MN的长度吗?(直接写出结果)
类型2 与线段中点有关的说明题
2.画线段MN=3
cm,在线段MN上取一点Q,使MQ=NQ;延长线段MN到点A,使AN=MN;延长线段NM到点B,使BM=BN.
(1)求线段BM的长;
(2)求线段AN的长;
(3)试说明点Q是哪些线段的中点.
INCLUDEPICTURE
"../../../训练角度2.tif"
\
MERGEFORMAT
线段分点问题
类型1 与线段分点有关的计算(设参法)
3.如图,B,C两点把线段AD分成2∶4∶3三部分,M是AD的中点,CD=6
cm,求线段MC的长.
(第3题)
类型2 线段分点与方程的结合
4.A,B两点在数轴上的位置如图,O为原点,现A,B两点分别以1个单位长度/秒,4个单位长度/秒的速度同时向左运动.
(1)几秒后,原点恰好在两点正中间?
(2)几秒后,恰好有OA∶OB=1∶2
(第4题)
专训四:线段上的动点问题
解决线段上的动点问题一般需注意:(1)找准点的各种可能的位置;(2)通常可用设元法,表示出移动变化后的线段的长(有可能是常数,那就是定值),再由题意列方程求解.
INCLUDEPICTURE
"../../../训练角度1.tif"
\
MERGEFORMAT
线段上动点与中点问题的综合
1.(1)如图①,D是线段AB上任意一点,M,N分别是AD,DB的中点,若AB=16,求MN的长;
(2)如图②,AB=16,点D是线段AB上一动点,M,N分别是AD,DB的中点,能否求出线段MN的长?若能,求出其长,若不能,试说明理由;
(3)如图③,AB=16,点D运动到线段AB的延长线上,其他条件不变,能否求出线段MN的长?若能,求出其长,若不能,试说明理由.
(4)你能用一句简洁的话,描述你发现的结论吗?
(第1题)
INCLUDEPICTURE
"../../../训练角度2.tif"
\
MERGEFORMAT
线段上动点问题中的存在性问题
2.如图,已知数轴上两点A,B对应的数分别为-2、6,O为原点,点P为数轴上的一动点,其对应的数为x.
(第2题)
(1)PA=________;PB=________(用含x的式子表示);
(2)在数轴上是否存在点P,使PA+PB=10?若存在,请求出x的值;若不存在,请说明理由.
(3)点P以1个单位长度/s的速度从点O向右运动,同时点A以5个单位长度/s的速度向左运动,点B以20个单位长度/s的速度向右运动,在运动过程中,M,N分别是AP,OB的中点,问:的值是否发生变化?请说明理由.
INCLUDEPICTURE
"../../../训练角度3.tif"
\
MERGEFORMAT
线段和差倍分关系中的动点问题
3.如图,线段AB=24,动点P从A出发,以每秒2个单位长度的速度沿射线AB运动,M为AP的中点.
(1)出发多少秒后,PB=2AM
(2)当P在线段AB上运动时,试说明2BM-BP为定值.
(3)当P在线段AB的延长线上运动时,N为BP的中点,下列两个结论:①MN长度不变;②MA+PN的值不变.选出正确的结论,并求出其值.
(第3题)
专训五:巧用角平分线的有关计算
角平分线的定义是进行角度计算常见的重要依据,因此解这类题要从角平分线找角的数量关系,利用图形中相等的角的位置关系,结合角的和、差关系求解.
INCLUDEPICTURE
"../../../训练角度1.tif"
\
MERGEFORMAT
角平分线间的夹角问题(分类讨论思想)
1.已知∠AOB=100°,∠BOC=60°,OM平分∠AOB,ON平分∠BOC,求∠MON的度数.
INCLUDEPICTURE
"../../../训练角度2.tif"
\
MERGEFORMAT
巧用角平分线解决折叠问题(折叠法)
2.如图,将一张长方形纸斜折过去,使顶点A落在A′处,BC为折痕,然后把BE折过去,使之落在A′B所在直线上,折痕为BD,那么两折痕BC与BD间的夹角是多少度?
(第2题)
INCLUDEPICTURE
"../../../训练角度3.tif"
\
MERGEFORMAT
巧用角平分线解决角的和、差、倍、分问
题(方程思想)
3.如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=19°,求∠AOB的度数.
(第3题)
INCLUDEPICTURE
"../../../训练角度4.tif"
\
MERGEFORMAT
巧用角平分线解决角的推理问题
(转化思想)
4.如图,已知OD,OE,OF分别为∠AOB,∠AOC,∠BOC的平分线,∠DOE和∠COF有怎样的关系?说明理由.
(第4题)
INCLUDEPICTURE
"../../../训练角度5.tif"
\
MERGEFORMAT
角平分线与线段中点的结合
5.如图,(1)已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数.
(3)如果(1)中∠BOC=β(β<90°),其他条件不变,求∠MON的度数.
(4)从(1)(2)(3)的结果中能得到什么样的规律?
(5)线段的计算与角的计算存在着紧密的联系,它们之间可以互相借鉴解法,请你模仿(1)~(4),设计一道以线段为背景的计算题,给出解答,并写出其中的规律.
(第5题)
专训六:巧解时针与分针的夹角问题
时钟时针、分针转动角度的问题,要注意时针转动一大格,转过角度为周角的十二分之一,即30°.每一个大格之间又分为5个小格,每个小格的角度是6°.注意时针与分针转动角度的速度比是1∶12,时针转动30°,分针转动360°.分针与秒针转动角度的速度之比是1∶60,分针转动6°(一个小格),秒针转动360°.
INCLUDEPICTURE
"../../../训练角度1.tif"
\
MERGEFORMAT
利用时间求角度
类型1 按固定时间求角度
1.(1)从上午11时到下午1时30分,这期间时针转过了________;下午1:30,时针、分针的夹角是________.
(2)3点20分时,时针与分针的夹角是多少度?
类型2 按动态时间求角度
2.小华是个数学迷,最近他在研究钟面角(时针与分针组成的角)问题,他想和大家一起来讨论相关问题.
(1)分针每分钟转6度,时针每分钟转________度;
(2)你能指出下面各个图中时针与分针之间夹角的大小吗?图①的钟面角为________度,图②的钟面角为________度.
(第2题)
(3)12:00时,时针和分针重合,至少经过多长时间会再次出现时针和分针重合的现象?此时,时针和分针各转动了多少度?
INCLUDEPICTURE
"../../../训练角度2.tif"
\
MERGEFORMAT
利用角度求时间(方程思想)
3.如图,观察时钟,解答下列问题.
(1)在2时和3时之间什么时刻,时针和分针的夹角为直角?
(第3题)
(2)小明下午五点多有事外出时,看到墙上钟面的时针和分针的夹角为90°,下午不到六点回家时,发现时针与分针的夹角又为90°,那么小明外出了多长时间?
专训一:线段或角的计数问题
1.几何计数问题应用广泛,解决方法是“有序数数法”,数数时要做到不重复、不遗漏.
2.解决这类问题要用到分类讨论思想及从特殊到一般的思想.
3.回顾前面线段、直线的计数公式,比较这些计数公式的区别与联系.
INCLUDEPICTURE
"../../../训练角度1.tif"
\
MERGEFORMAT
线段条数的计数问题
1.先阅读文字,再解答问题.
(第1题)
如图,在一条直线上取两点,可以得到1条线段,在一条直线上取三点可得到3条线段,其中以A1为端点的向右的线段有2条,以A2为端点的向右的线段有1条,所以共有2+1=3(条).
(1)在一条直线上取四个点,以A1为端点的向右的线段有______条,以A2为端点的向右的线段有_________________________________________________________________条,
以A3为端点的向右的线段有______条,共有______+______+______=______(条).
(2)在一条直线上取五个点,以A1为端点的向右的线段有______条,以A2为端点的向右的线段有________条,以A3为端点的向右的线段有________条,以A4为端点的向右的线段有______条,共有______+______+______+______=____(条).
(3)在一条直线上取n个点(n≥2),共有________条线段.
(4)某学校七年级共有6个班进行辩论赛,规定进行单循环赛(每两个班赛一场),那么该校七年级的辩论赛共要进行多少场?
(5)乘火车从A站出发,沿途经过5个车站方可到达B站,那么A,B两站之间最多有多少种不同的票价?需要安排多少种不同的车票?
INCLUDEPICTURE
"../../../训练角度2.tif"
\
MERGEFORMAT
平面内直线相交所得交点与平面的计数问题
2.为了探究同一平面内的几条直线相交最多能产生多少个交点,能把平面最多分成几部分,我们从最简单的情形入手,如图所示.
(第2题)
列表如下:
直线条数
最多交点个数
平面最多分成部分数
1
0
2
2
1
4
3
3
7
…
…
…
(1)当直线条数为5时,最多有________个交点,可写成和的形式为__________;把平面最多分成________部分,可写成和的形式为__________;
(2)当直线条数为10时,最多有________个交点,把平面最多分成________部分;
(3)当直线条数为n时,最多有多少个交点?把平面最多分成多少部分?
INCLUDEPICTURE
"../../../训练角度3.tif"
\
MERGEFORMAT
关于角的个数的计数问题
3.有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点,如图,如果过∠BAC的顶点A:
(1)在角的内部作一条射线,那么图中一共有几个角?
(2)在角的内部作两条射线,那么图中一共有几个角?
(3)在角的内部作三条射线,那么图中一共有几个角?
(4)在角的内部作n条射线,那么图中一共有几个角?
(第3题)
专训二:分类思想在线段和角的计算中的应用
解答有关点和线的位置关系、线段条数或长度、角的个数或大小等问题时,由于题目中没有给出具体的图形,而根据题意又可能出现多种情况,就应不重不漏地分情况加以讨论,这种思想称为分类讨论思想.需要进行分类讨论的题目,综合性一般较强.
INCLUDEPICTURE
"../../../应用1.tif"
\
MERGEFORMAT
分类思想在线段的计算中的应用
1.已知线段AB=12,在线段AB上有C,D,M,N四点,且AC∶CD∶DB=1∶2∶3,AM=AC,DN=DB,求线段MN的长.
2.如图,点O为原点,点A对应的数为1,点B对应的数为-3.
(1)若点P在数轴上,且PA+PB=6,求P对应的数;
(2)若点M在数轴上,且MA∶MB=1∶3,求M对应的数;
(3)若点A的速度为5个单位长度/秒,点B的速度为2个单位长度/秒,点O的速度为1个单位长度/秒,A,B,O同时向右运动,几秒后,点O恰为线段AB的中点?
(第2题)
INCLUDEPICTURE
"../../../应用2.tif"
\
MERGEFORMAT
分类思想在角的计算中的应用
3.如图,已知∠AOC=2∠BOC,∠AOC的余角比∠BOC小30°.
(1)求∠AOB的度数;
(2)过点O作射线OD,使得∠AOC=4∠AOD,请你求出∠COD的度数.
(第3题)
4.已知OM和ON分别平分∠AOC和∠BOC.
(1)如图,若OC在∠AOB的内部时,探究∠MON与∠AOB的数量关系;
(2)若OC在∠AOB的外部,且OC不与OA,OB重合时,请你画出图形,并探究∠MON与∠AOB的数量关系.(提示:分三种情况讨论)
(第4题)
专训三:几种常见的热门考点
本章知识从大的方面可分为两部分,第一部分是立体几何的初步认识,第二部分是平面图形的认识,这些都是几何学习的基础.本章主要考查立体图形的识别、立体图形的三视图,图形的展开与折叠,直线、射线、线段及角的有关计算.立体图形的平面展开图,三视图等是中考中常见考点,通常以选择、填空形式呈现.
INCLUDEPICTURE
"../../../热门考点1.tif"
\
MERGEFORMAT
立体图形的识别
1.在①球体;②柱体;③圆锥;④棱柱;⑤棱锥中,必是多面体(指由四个或四个以上多边形所围成的立体图形)的是( )
A.①②③④⑤
B.②和③
C.④
D.④和⑤
2.如图所示的立体图形中,是柱体的是________.(填序号)
(第2题)
INCLUDEPICTURE
"../../../热门考点2.tif"
\
MERGEFORMAT
立体图形的三视图
3.(2015·泰安)下列四个几何体(如图):
(第3题)
其中左视图与俯视图相同的几何体共有( )个.
A.1 B.2 C.3 D.4
4.一个几何体的三视图如图所示,则这个几何体是( )
A.四棱锥
B.四棱柱
C.三棱锥
D.三棱柱
(第4题)
(第5题)
5.由一些完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则组成这个几何体的小正方体的个数可能是__________.
INCLUDEPICTURE
"../../../热门考点3.tif"
\
MERGEFORMAT
图形的展开与折叠
6.小亮为今年参加中考的好友小杰制作了一个正方体礼品盒(如图),六个面上各有一个字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的表面展开图可能是( )
eq
\a\vs4\al(,,,) eq
\a\vs4\al()
(第6题)
7.如图是一个长方体形状包装盒的表面展开图.折叠制作完成后得到长方体的容积是(包装材料厚度不计)( )
(第7题)
A.40×40×70
B.70×70×80
C.80×80×80
D.40×70×80
INCLUDEPICTURE
"../../../热门考点4.tif"
\
MERGEFORMAT
直线、射线、线段
8.下列关于作图的语句中正确的是( )
A.画直线AB=10厘米
B.画射线OB=10厘米
C.已知A,B,C三点,过这三点画一条直线
D.过直线AB外一点画一条直线和直线AB相交
9.如图,已知线段AB,在BA的延长线上取一点C,使CA=3AB,则线段CA与线段CB的长度之比为( )
(第9题)
A.3∶4
B.2∶3
C.3∶5
D.1∶2
10.开学整理教室时,老师总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌摆在一条线上,整整齐齐,这是因为________________________.
11.乘火车从A站出发,沿途经过3个车站方可到达B站,那么A,B两站之间需要安排________种不同的车票.
12.如图,已知AB和CD的公共部分BD=AB=CD,线段AB,CD的中点E,F之间的距离是10
cm,求AB,CD的长.
(第12题)
INCLUDEPICTURE
"../../../热门考点5.tif"
\
MERGEFORMAT
角及角的有关计算
13.有下列说法:
①两条射线所组成的图形叫做角;
②一条射线旋转而成的图形叫做角;
③两边成一条直线的角是平角;
④平角是一条直线.
其中正确的个数是( )
A.1
B.2
C.3
D.4
14.4点10分,时针与分针所夹的小于平角的角为( )
A.55°
B.65°
C.70°
D.以上结论都不对
15.如图所示,两块三角板的直角顶点O重合在一起,且OB恰好平分∠COD,则∠AOD的度数是________度.
(第15题)
16.若一个角的余角比它的补角的少20°,则这个角的度数为________.
17.如图,O是直线AB上一点,OC,OD是从O点引出的两条射线,OE平分∠AOC,∠BOC∶∠AOE∶∠AOD=2∶5∶8,求∠BOD的度数.
(第17题)
INCLUDEPICTURE
"../../../热门考点6.tif"
\
MERGEFORMAT
数学思想方法的应用
a.数形结合思想
18.往返于A,B两个城市的客车,中途有三个停靠站,分别为C,D,E.
(1)最多共有多少种不同的票价?
(2)要准备多少种车票?
b.方程思想
19.互为补角的两个角的度数之比是5∶4,求这两个角的度数.
c.分类讨论思想
20.已知同一平面内四点,过其中任意两点画直线,仅能画4条,则这四个点的位置关系是( )
A.任意三点不在同一条直线上
B.四点在同一条直线上
C.最多三点在同一条直线上
D.三点在同一条直线上,第四点在这条直线外
21.已知一条射线OA,若从点O再引两条射线OB和OC,使∠AOB=80°,∠BOC=40°,若OD平分∠AOC,则∠BOD等于________.
d.转化思想
22.如图所示,一观测塔的底座部分是四棱柱,现要从下底面A点修建钢筋扶梯,经过点M,N到点D′(M在BB′上,N在CC′上),再进入顶部的观测室,已知AB=BC=CD,试确定使扶梯的总长度最小的点M,N的位置.
(第22题)
答案
专训一
1.C
2.④ ①③⑥
3.解:(1)按柱体、锥体、球体分:①③⑤⑥⑦为柱体;④⑧为锥体;②为球体.(分类标准不唯一)
(2)③是圆柱,圆柱的上、下底面都是圆,侧面是一个曲面;⑥是五棱柱,上、下底面是形状、大小相同的五边形,侧面是5个长方形,侧面的个数与底面边数相等.
相同点:两者都有两个底面,且两个底面的形状,大小相同.
不同点:圆柱的底面是圆,五棱柱的底面是五边形.圆柱的侧面是一个曲面,五棱柱的侧面由5个长方形组成.
4.C 5.有
6.①③④⑤⑥ ②③④⑥
7.解:有曲面的是③④⑤;无曲面的是①②⑥⑦.
专训二
1.B
2.解:题图①②③④⑥都是正方体的平面展开图.
3.解:(1)如果面A是长方体的上面,那么面C会在下面.
(2)如果面F是长方体的后面,从左面看是面B,那么向外折时面C会在上面,向里折时面A会在上面.
(3)从右面看是面A,从上面看是面E,那么向外折时从前面看是面B,向里折时从前面看是面D.
4.解:①三棱锥;②四棱锥;③五棱锥;④三棱柱;⑤圆柱;⑥圆锥.
点拨:棱锥和棱柱的共同点是棱锥、棱柱都是以底面多边形的边数来命名的,如三棱锥是指底面为三角形的棱锥,而五棱柱是指底面为五边形的棱柱.它们的不同点是棱柱的侧棱互相平行,而棱锥的侧棱交于一点.
5.(8n-4) 点拨:从下往上数两个面涂色的小立方体个数,图①中:第一层4个,第二层0个;图②中:第一层4个;第二层4个,第三层4个;图③中,第一层4个,第二层4个,第三层4个,第四层8个,故第n个几何体中涂两个面的小立方体有[4n+4(n-1)]个,即(8n-4)个.
6.解:能围成,体积为40×70×65=182
000(cm3).
答:体积为182
000
cm3.
阶段强化专题训练
专训三
1.解:(1)分两种情况:①当点C在线段AB上时,如图①,因为M为AB的中点,所以MB=AB=×20=10(cm).因为N为BC的中点,所以BN=BC=×8=4(cm),所以MN=MB-BN=10-4=6(cm);
(第1题)
②当点C在线段AB的延长线上时,如图②,因为M为AB的中点,所以MB=AB=×20=10(cm).因为N为BC的中点,所以BN=BC=×8=4(cm),所以MN=MB+BN=10+4=14(cm).
(2)MN=(a+b)或MN=(a-b).
2.解:如图.
(第2题)
(1)因为BM=BN,所以BM=MN.
因为MN=3
cm,所以BM=×3=1.5(cm).
(2)因为AN=MN,MN=3
cm.所以AN=1.5
cm.
(3)MN=3
cm,MQ=NQ,所以MQ=NQ=1.5
cm.
所以BQ=BM+MQ=1.5+1.5=3(cm),
AQ=AN+NQ=3
cm.所以BQ=QA.
所以Q是线段MN的中点,也是线段AB的中点.
3.解:设AB=2k
cm,则BC=4k
cm,CD=3k
cm,AD=2k+4k+3k=9k(cm).因为CD=6
cm,即3k=6,所以k=2,则AD=18
cm.又因为M是AD的中点,所以MD=AD=×18=9(cm).所以MC=MD-CD=9-6=3(cm).
4.解:(1)设运动时间为x秒,依题意得x+3=12-4x,解得x=1.8.
答:1.8秒后,原点恰好在两点正中间.
(2)设运动时间为t秒.
①B与A相遇前:12-4t=2(t+3),即t=1;
②B与A相遇后:4t-12=2(t+3),即t=9.
答:1秒或9秒后,恰好有OA∶OB=1∶2.
专训四
1.解:(1)MN=DM+DN=AD+BD=(AD+BD)=AB=8.
(2)能.MN=DM+DN=AD+BD=(AD+BD)=AB=8.
(3)能.MN=MD-DN=AD-BD=(AD-BD)=AB=8.
(4)MN的长始终等于AB长的一半.
2.解:(1)|x+2| |x-6|
(2)分三种情况:
①当点P在A,B之间时,PA+PB=8,故舍去;
②当点P在B点右边时,PA=x+2,PB=x-6,因为(x+2)+(x-6)=10,所以x=7;
③当点P在A点左边时,PA=-x-2,PB=6-x,因为(-x-2)+(6-x)=10,所以x=-3.
所以当x=-3或7时,PA+PB=10,
(3)的值不发生变化,理由如下:
设运动时间为t
s.
则OP=t,OA=5t+2,OB=20t+6,AB=OA+OB=25t+8,AB-OP=24t+8,AP=OA+OP=6t+2,AM=AP=3t+1,OM=OA-AM=5t+2-(3t+1)=2t+1,ON=OB=10t+3,所以MN=OM+ON=12t+4,所以==2,即的值不发生变化.
3.解:(1)设出发x秒后,PB=2AM,则PA=2x,PB=24-2x,AM=x,所以24-2x=2x,即x=6.
(2)设运动时间为t秒,则BM=24-t,PB=24-2t,所以2BM-BP=2(24-t)-(24-2t)=24,即2BM-BP为定值.
(3)因为PA=2t,AM=PM=t,PB=2t-24,PN=PB=t-12,
所以①MN=PM-PN=t-(t-12)=12.
所以MN长度不变,为定值;
②MA+PN=t+t-12=2t-12,
所以MA+PN的值是变化的.
综上所述,正确的结论是①,且MN=12.
专训五
1.解:分两种情况:(1)如图①,当OC落在∠AOB的内部时,
因为OM平分∠AOB,ON平分∠BOC,
所以∠BOM=∠AOB=×100°=50°,∠BON=∠BOC=×60°=30°,
所以∠MON=∠BOM-∠BON=50°-30°=20°.
(第1题)
(2)如图②,当OC落在∠AOB的外部时,
因为OM平分∠AOB,ON平分∠BOC,
所以∠BOM=∠AOB=×100°=50°,∠BON=∠BOC=×60°=30°.
所以∠MON=∠BOM+∠BON=50°+30°=80°.
综上可知,∠MON的度数为20°或80°.
点拨:本题已知中没有图,作图时应考虑OC落在∠AOB的内部和外部两种情况,体现了分类讨论思想的运用.
2.解:因为∠CBA与∠CBA′折叠重合,所以∠CBA=∠CBA′.
因为∠EBD与∠A′BD折叠重合,
所以∠EBD=∠A′BD.
又因为这四个角的和是180°,
所以∠CBD=∠CBA′+∠A′BD=×180°=90°.
即两折痕BC与BD间的夹角为90°.
点拨:本题可运用折叠法动手折叠,便于寻找角与角之间的关系.
3.解:设∠AOC=x,则∠COB=2x.
因为OD平分∠AOB,所以∠AOD=∠AOB=(∠AOC+∠BOC)=x.
又因为∠DOC=∠AOD-∠AOC,所以19°=x-x,
解得x=38°.所以∠AOB=3x=3×38°=114°.
点拨:根据图形巧设未知数用角与角之间的数量关系构建关于未知数的方程求出角的度数体现了方程思想的运用.
4.解:∠DOE=∠COF.理由如下:
因为OD平分∠AOB,所以∠DOB=∠AOB.
因为OF平分∠BOC,所以∠BOF=∠BOC,所以∠DOB+∠BOF=∠AOB+∠BOC=∠AOC,即∠DOF=∠AOC.又因为OE平分∠AOC,所以∠EOC=∠AOC,所以∠DOF=∠EOC.又因为∠DOF=∠DOE+∠EOF,∠EOC=∠EOF+∠COF,所以∠DOE=∠COF.
点拨:欲找出∠DOE与∠COF的关系只要找到∠DOF与∠COE的关系即可.而OD,OF分别是∠AOB,∠BOC的平分线,那么由此可得到∠DOF与∠AOC的关系,而且又有∠AOC=2∠COE,即可转化成∠DOF与∠COE的关系,进而可得到∠DOE与∠COF的关系,体现了转化思想的运用.
5.解:(1)因为OM平分∠AOC,ON平分∠BOC,
所以∠MOC=∠AOC,∠NOC=∠BOC,
所以∠MON=∠MOC-∠NOC=∠AOC-∠BOC=(∠AOB+∠BOC)-∠BOC=∠AOB=45°.
(2)∠MON=∠AOB=.
(3)∠MON=∠AOB=45°.
(4)从(1)(2)(3)的结果中可看出:∠MON的大小总等于∠AOB大小的一半,而与∠BOC的大小变化无关.
(5)可设计的问题为:如图,线段AB=a,延长AB到C使BC=b,点M,N分别是线段AC,BC的中点,求线段MN的长.
(第5题)
解:因为点M,N分别是线段AC,BC的中点,
所以MC=AC,NC=BC.
所以MN=MC-NC=(AC-BC)=AB=a.
规律:线段MN的长度总等于线段AB长度的一半,而与线段BC的长度变化无关.
专训六
1.解:(1)75° 135°
(2)时针每小时转30°,分针每分钟转6°.时针从指向12开始转过的角度为3×30°=100°,分针从指向12开始转过的角度为20×6°=120°,120°-100°=20°,即3点20分时,时针与分针的夹角是20°.
2.解:(1)0.5 (2)30 22.5
(3)设至少x分钟后分针与时针再次重合,则6x-0.5x=360,解得x=,
即至少经过分钟会再次出现时针与分针重合的现象.
×0.5°=° ×6°=°
答:时针转了°,分针转了°.
3.解:(1)设从2时经过x分,分针与时针的夹角为直角,依题意,有×6°=90°,解得x=.
答:在2时分时,时针和分针的夹角为直角.
(2)设小明外出了y分钟,则时针走了0.5y度,分针走了6y度.
根据题意,列方程为6y=90+0.5y+90,解得y=.
答:小明外出了分钟.
点拨:在钟表问题中,常利用时针与分针的转动度数关系:分针每分转动6°,时针每分转动0.5°,并且结合起点时时针和分针的位置关系建立角的数量关系.
全章整合提升密码
专训一
1.解:(1)3 2 1 3 2 1 6 (2)4 3 2 1 4 3 2 1 10
(3)
(4)七年级有6个班,类似于一条直线上有6个点,每两个班赛一场,类似于两点之间有一条线段,那么七年级的辩论赛共要进行=15(场).
(5)从A站出发,沿途经过5个车站到达B站,类似于一条直线上有7个点,此时共有线段=21(条),即A,B两站之间最多有21种不同的票价.因为来往两站的车票起点与终点不同,所以A,B两站之间需要安排21×2=42(种)不同的车票.
2.解:(1)10 1+2+3+4 16 1+1+2+3+4+5
(2)45 56
(3)当直线条数为n时,
最多有1+2+3+…+(n-1)=(个)交点;
把平面最多分成1+1+2+3+…+n=部分.
3.解:(1)如题图①,已知∠BAC,如果在其内部作一条射线,显然这条射线就会和∠BAC的两条边都组成一个角,这样一共就有1+2=3(个)角.
(2)题图①中有1+2=3(个)角,如果再在题图①的角的内部增加一条射线,即为题图②,显然这条射线就会和图中的其他三条射线再组成三个角,即题图②中共有1+2+3=6(个)角.
(3)如题图③,在角的内部作三条射线,即在题图②中再增加一条射线,同样这条射线就会和图中的其他四条射线再组成四个角,即题图③中共有1+2+3+4=10(个)角.
(4)综上所述,如果在一个角的内部作n条射线,则图中共有1+2+3+…+n+(n+1)=(个)角.
专训二
1.解:因为AB=12,AC∶CD∶DB=1∶2∶3,
所以AC=AB=12×=2,CD=AB=12×=4,DB=AB=12×=6.
因为AM=AC,DN=DB,
所以MC=AC=2×=1,DN=DB=6×=.
①当点N在点D右侧时,如图①,
MN=MC+CD+DN=1+4+=;
(第1题)
②当点N在点D左侧时,如图②,
MN=MC+CD-DN=1+4-=.
综上所述,线段MN的长为或.
点拨:首先要根据题意,画出图形.由于点N的位置不确定,故要考虑分类讨论.
2.解:(1)①当点P在A,B之间时,不合题意,舍去;
②当点P在A点右边时,点P对应的数为2;
③当点P在B点左边时,点P对应的数为-4.
(2)①当M在线段AB上时,M对应的数为0;
②当M在线段BA的延长线上时,M对应的数为3;
③当M在线段AB的延长线上时,不合题意,舍去.
(3)设运动x秒时,点B运动到点B′,点A运动到点A′,点O运动到点O′,此时O′A′=O′B′,点A′,B′在点O′两侧,则BB′=2x,OO′=x,AA′=5x,
所以点B′对应的数为2x-3,点O′对应的数为x,点A′对应的数为5x+1,
因为O′A′=5x+1-x=4x+1,O′B′=x-(2x-3)=3-x,所以
4x+1=3-x,解得x=0.4.
即0.4秒后,点O恰为线段AB的中点.
3.解:(1)设∠BOC=x,则∠AOC=2x,
由题意得90°-2x+30°=x,解得x=40°.
因为∠AOC=2∠BOC,所以∠AOB=∠BOC=40°.
(2)情况一:当OD在∠AOC内部时,如图①,
由(1)得∠AOC=80°.
因为∠AOC=4∠AOD,所以∠AOD=20°,
所以∠COD=∠AOC-∠AOD=80°-20°=60°.
(第3题)
情况二:当OD在∠AOC外部时,如图②,
由(1)得∠AOC=80°.
因为∠AOC=4∠AOD,所以∠AOD=20°,
所以∠COD=∠AOD+∠AOC=20°+80°=100°.
综上所述,∠COD的度数为60°或100°.
4.解:(1)因为OM和ON分别平分∠AOC和∠BOC,
所以∠MOC=∠AOC,∠NOC=∠BOC.
所以∠MON=∠MOC+∠NOC=∠AOC+∠BOC=(∠AOC+∠BOC)=∠AOB.
(2)情况一:如图①,
因为OM和ON分别平分∠AOC和∠BOC,
所以∠MOC=∠AOC=(∠AOB+∠BOC),∠NOB=∠BOC.
所以∠MON=∠MOB+∠NOB=∠MOC-∠BOC+∠BOC=∠MOC-∠BOC=(∠AOB+∠BOC)-∠BOC=∠AOB.
(第4题)
情况二:如图②,
因为OM和ON分别平分∠AOC和∠BOC,
所以∠AOM=∠AOC,∠NOC=∠BOC=(∠AOB+∠AOC)=∠AOB+∠AOC.
所以∠MON=∠AOM+∠AON=∠AOC+(∠NOC-∠AOC)=∠NOC-∠AOC=∠AOB+∠AOC-∠AOC=∠AOB.
情况三,如图③,
因为OM和ON分别平分∠AOC和∠BOC,
所以∠MOC=∠AOC,∠NOC=∠BOC.
所以∠MON=∠MOC+∠NOC=∠AOC+∠BOC=(∠AOC+∠BOC)=(360°-∠AOB)=180°-∠AOB.
综上所述,∠MON与∠AOB的数量关系是∠MON=∠AOB或∠MON=180°-∠AOB.
专训三
1.D 2.②③ 3.D 4.B 5.4或5或6或7 6.C 7.D 8.D
9.A 10.两点确定一条直线
11.20
12.解:因为BD=AB=CD,所以CD=AB.
因为F是CD的中点,
所以DF=CD=×AB=AB.
因为E是AB的中点,所以EB=AB,
所以ED=EB-DB=AB-AB=AB.
所以EF=ED+DF=AB+AB=AB=10
cm,
所以AB=12
cm,所以CD=AB=16
cm.
13.A 14.B 15.135 16.40°
17.解:设∠BOC=2x°,则∠AOE=5x°,∠AOD=8x°.
因为O是直线AB上一点,所以∠AOB=180°,
所以∠COE=(180-7x)°.
因为OE平分∠AOC,所以∠AOE=∠COE,
即5x=180-7x,解得x=15,
所以∠AOD=8×15°=120°,所以∠BOD=60°.
18.解:(1)根据题意画出示意图,如图所示,线段有AC,AD,AE,AB,CD,CE,CB,DE,DB,EB,共10条,因此最多共有10种不同的票价.
(2)同一路段,往返时起点和终点正好相反,所以要准备20种车票.
(第18题)
19.解:设这两个角分别为5x°,4x°.
因为这两个角互补,所以5x+4x=180,解得x=20.
5x=100,4x=80,
所以这两个角分别为100°,80°.
20.D 21.60°或20°
22.解:画出四棱柱的侧面展开图,点M,N的位置如图①所示,则M,N在四棱柱上的位置如图②所示.
(第22题)
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
