人教版数学必修一教学3.1.2用二分法求方程的近似解课件
文档属性
| 名称 | 人教版数学必修一教学3.1.2用二分法求方程的近似解课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 495.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-25 00:00:00 | ||
图片预览











文档简介
课件62张PPT。3.1.2
用二分法求方程的近似解【知识提炼】
1.二分法的定义
(1)满足的条件:
在区间[a,b]上_________的函数y=f(x)且在区间端点的函数值满足:
_____________.连续不断f(a)·f(b)<0(2)操作过程:
把函数f(x)的零点所在的区间_________,使区间的两个端点逐步逼
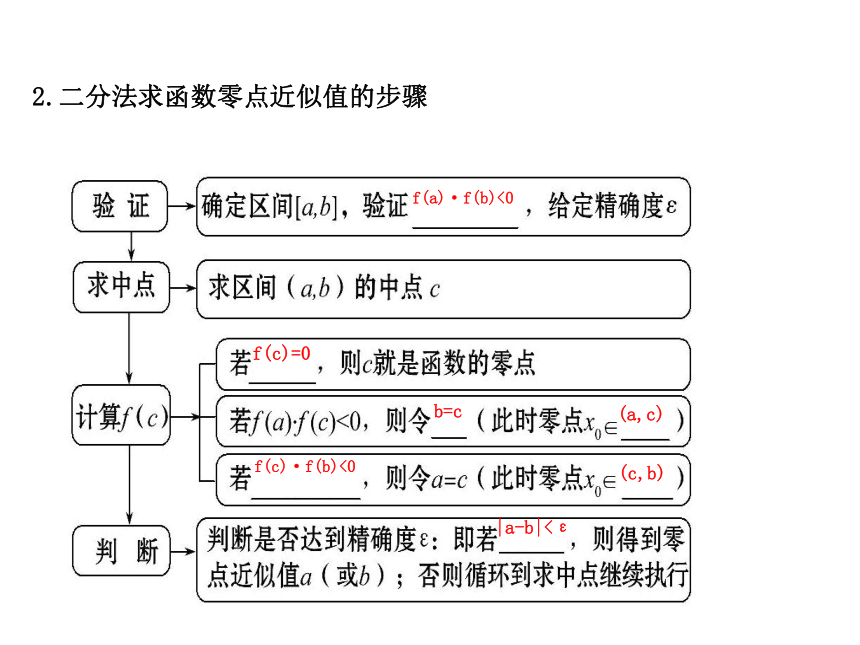
近_____,进而得到零点的近似值. 一分为二零点2.二分法求函数零点近似值的步骤f(a)·f(b)<0f(c)=0b=cf(c)·f(b)<0(a,c)(c,b)|a-b|<ε【即时小测】
1.思考下列问题
(1)所有函数的零点都能用二分法求其所在的区间吗?
提示:不是所有的函数都能用二分法来判断零点所在的区间.只有图象在给定区间上是连续不断的,且在区间的端点处的函数值是异号的函数,才可以用二分法求函数的零点所在的区间.(2)用二分法求方程的近似解时,如何决定步骤的结束?
提示:看清题目的精确度,当零点所在区间的两个端点值之差的绝对值小于精确度时,则二分法步骤结束. 2.下列函数不宜用二分法求零点的是 ( )
A.f(x)=x3-2 B.f(x)=lnx-3
C.f(x)=x2+2 x+2 D.f(x)=-x2+4x-1
【解析】选C.因为f(x)=x2+2 x+2=(x+ )2≥0,即含有零点的区间
[a,b]不满足f(a)·f(b)<0.3.用二分法求函数f(x)=x3+5的零点可以选取的初始区间是 ( )
A.[-2,1] B.[-1,0]
C.[0,1] D.[1,2]
【解析】选A.由于f(-2)=(-2)3+5=-3<0,f(1)=1+5=6>0,所以可选取
[-2,1]作为初始区间.4.已知二次函数f(x)=x2-x-6在区间[1,4]上的图象是一条连续的曲线,且f(1)=-6<0,f(4)=6>0,由零点存在性定理可知函数在[1,4]内有零点,用二分法求解时,取(1,4)的中点a,则f(a)= .
【解析】由于(1,4)的中点a= ,则
答案:-2.255.在用二分法求方程f(x)=0在区间[0,1]上的近似解时,经计算,f(0.425)>0,f(0.552)>0,f(0.605)<0,即得到方程的一个近似解为 .(精确度为0.1)
【解析】因为|0.605-0.552|=0.053<0.1,
所以可取0.605或0.552作为方程f(x)=0的一个近似解.
答案:0.605或0.552【知识探究】
知识点 二分法的概念及利用其求函数零点的近似值
观察图形,回答下列问题:
问题1:上图中的线路出现故障,你能否设计一个维修方案来迅速查出故障所在?
问题2:利用二分法求函数零点时应把握哪几个关键点?【总结提升】
1.理解二分法的含义时要注意的两点
(1)二分法是求函数零点近似值的一种方法,根据题目要求的精确度,只需进行有限次运算即可.
(2)它的根据是根的存在性定理.
2.二分法求函数零点的两个关键点
(1)初始区间的选取,符合条件(包括零点),又要使其长度尽量小.
(2)进行精确度的判断,以决定是停止计算还是继续计算.【题型探究】
类型一 二分法概念的理解
【典例】1.(2015·昌平高一检测)关于“二分法”求方程的近似
解,说法正确的是 ( )
A.“二分法”求方程的近似解一定可将y=f(x)在[a,b]内的所有零
点得到
B.“二分法”求方程的近似解有可能得不到y=f(x)在[a,b]内的零点
C.应用“二分法”求方程的近似解,y=f(x)在[a,b]内有可能无零点
D.“二分法”求方程的近似解可能得到f(x)=0在[a,b]内的精确解2.通过下列函数的图象,判断能用“二分法”求其零点的是 ( )【解题探究】1.二分法的实质是什么?
提示:二分法就是通过不断选取区间的中点,将所选区间一分为二,逐步逼近,从而获得零点的近似值.2.典例2中能用“二分法”求零点的函数图象有什么特征?
提示:其特征为:图象经过x轴,且与x轴交点处两侧的函数值符号相反.【解析】1.选D.二分法求零点,则一定有且能求出,故B,C不正确;零点左侧与右侧的函数值符号相同的零点不能用二分法得到,故A不正确,故选D.
2.选C.在A中,函数无零点.在B和D中,函数有零点,但它们在零点左右的函数值符号相同,因此它们都不能用二分法来求零点.而在C中,函数图象是连续不断的,且图象与x轴有交点,并且在交点处两侧的函数值符号相反,所以C中的函数能用二分法求其零点.【方法技巧】运用二分法求函数的零点应具备的条件
(1)函数图象在零点附近连续不断.
(2)在该零点左右函数值异号.
只有满足上述两个条件,才可用二分法求函数零点.【变式训练】用“二分法”可求近似解,对于精确度ε说法正确的
是 ( )
A.ε越大,零点的精确度越高
B.ε越大,零点的精确度越低
C.重复计算次数就是ε
D.重复计算次数与ε无关
【解析】选B.精确度ε决定计算的次数,其直接影响零点的精确度,ε越大,零点的精确度越低,ε越小,零点的精确度越高.类型二 用二分法求函数的零点
【典例】(2015·塘沽高一检测)求函数f(x)=x3-3x2-9x+1的一个负零点(精确度0.01).
【解题探究】典例中应先怎样判断负零点所在的区间?
提示:可借助零点的判断方法确定出负零点所在的区间,再利用二分法逐步确定.【解析】确定一个包含负数零点的区间(m,n),且f(m)·f(n)<0.因为f(-1)>0,f(-2)<0,
所以可以取区间(-2,-1)作为计算的初始区间,
当然选取再较大的区间也可以.用二分法逐次计算,列表如下:由于|-1.929 687 5+1.937 5|=0.007 812 5<0.01,所以函数的一个负零点近似值可取为-1.929 687 5.【延伸探究】
1.(变换条件)若本例改为“试判断函数f(x)=x3-3x2-9x+1在[-2,-1]
内有无零点,如果有,求出一个近似零点(精确度0.1)”又如何求解呢?【解析】因为f(-1)>0,f(-2)<0,且函数f(x)=x3-3x2-9x+1的图象是连续的曲线,根据函数零点的存在性定理可知,它在区间[-2,-1]内有零点,用二分法逐步计算,列表如下:由于|-1.875+1.937 5|=0.062 5<0.1,所以函数在区间[-2,-1]内的一个近似零点可取为-1.937 5.2.(变换条件、改变问法)若将函数改为“f(x)=x3+2x2-3x-6”,如何求该函数的正数零点?(精确度0.1)
【解析】确定一个包含正数零点的区间(m,n),且f(m)·f(n)<0.
因为f(0)=-6<0,f(1)=-6<0,f(2)=4>0,
所以可以取区间(1,2)作为计算的初始区间,
用二分法逐次计算,列表如下:由于|1.75-1.687 5|=0.062 5<0.1.所以函数的正数零点的近似值可取为1.687 5.【方法技巧】
1.用二分法求函数零点的近似值应遵循的原则
(1)需依据图象估计零点所在的初始区间[m,n](一般采用估计值的方法完成).
(2)取区间端点的中点c,计算f(c),确定有解区间是(m,c)还是(c,n),逐步缩小区间的“长度”,直到区间的两个端点符合精确度要求,终止计算,得到函数零点的近似值.2.二分法求函数零点步骤的记忆口诀
定区间,找中点;中值计算两边看.
同号丢,异号算,零点落在异号间.
重复做,何时止,精确度来把关口.【补偿训练】试确定函数f(x)= x+x-4零点的个数.
【解析】设y1= x,y2=4-x,则f(x)的零点个数即y1= x,y2=4-x的
图象的交点个数,
作出两函数大致图象,如图:由图知y1= x与y2=4-x的图象有两个交点,其中一个交点横坐标在区间(0,1)之内,另一个大于4.
因此函数f(x)= x+x-4零点的个数有两个.【延伸探究】
1.(改变问法)若本题条件不变,试求出其中最大零点的近似值.(精确
度0.1)
【解析】设y1= x,y2=4-x,则f(x)的零点个数即y1= x,y2=4-x的
图象的交点个数,
作出两函数大致图象,如图:由图知y1= x与y2=4-x的图象有两个交点,其中一个交点横坐标在
区间(0,1)之内,另一个大于4.
因为f(6)= 6+6-4= 6+2< 4+2=0,
f(7)= 7+7-4= 7+3> 8+3=0,
结合图象可知,另一个交点的横坐标在区间(6,7)之内,
综上分析知,函数f(x)= x+x-4在区间(6,7)内有最大零点x0,取区
间(6,7)的中点x1=6.5,用计算器算得f(6.5)≈-0.200,
因为f(6.5)·f(7)<0,
所以x0∈(6.5,7),
再取区间(6.5,7)的中点x2=6.75,
用计算器算得f(6.75)≈-0.005,
因为f(6.75)·f(7)<0,
所以x0∈(6.75,7).再取区间(6.75,7)的中点x3=6.875,
用计算器算得f(6.875)≈0.094,
因为f(6.75)·f(6.875)<0,
所以x0∈(6.75,6.875).再取区间(6.75,6.875)的中点x4=6.8125,用计算器算得f(6.8125)≈0.443,
因为f(6.8125)·f(6.75)<0,
所以x0∈(6.75,6.8125)由于|6.75-6.8125|=0.0625<0.1,
所以函数f(x)= x+x-4最大零点的近似值可取6.8125.2.(变换条件)将函数改为“f(x)=log2x+x-4”,试判断函数零点个数;并求零点的近似值.(精确度0.1)
【解析】设y1=log2x,y2=4-x,则f(x)的零点个数即y1=log2x,y2=4-x的图象的交点个数.
作出两函数的大致图象,如图:由图知,y1=log2x与y2=4-x的图象只有一个交点,
因为f(2)=log22+2-4=-1<0,
f(3)=log23+3-4=log23-1>log22-1=0,
所以函数f(x)=log2x+x-4只有一个零点,在区间(2,3)内.
取区间(2,3)的中点x1=2.5,
用计算器算得f(2.5)≈-0.178,
因为f(2.5)·f(3)<0,所以x0∈(2.5,3).再取区间(2.5,3)的中点x2=2.75,
用计算器算得f(2.75)≈0.209,
因为f(2.5)·f(2.75)<0,所以x0∈(2.5,2.75).
再取区间(2.5,2.75)的中点x3=2.625,
用计算器算得f(2.625)≈0.017,
因为f(2.5)·f(2.625)<0,所以x0∈(2.5,2.625).
再取区间(2.5,2.625)的中点x4=2.5625,用计算器算得f(2.5625)≈-0.080,
因为f(2.5625)·f(2.625)>0,所以x0∈(2.5625,2.625).
由于|2.625-2.5625|=0.0625<0.1,
所以函数f(x)=log2x+x-4零点的近似值可取2.5625.类型三 用二分法求方程的近似解
【典例】1.(2015·包头高一检测)设f(x)=3x+3x-8,用二分法求方程3x+3x-8=0在x∈(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,
f(1.25)<0,则方程的根落在区间( )
A.(1,1.25) B.(1.25,1.5)
C.(1.5,2) D.不能确定
2.借助计算器,用二分法求出方程ln(2x+6)+2=3x在区间(1,2)内的近似解(精确度0.2).【解题探究】1.典例1中方程3x+3x-8=0在x∈(1,2)内有解应具备什么条件?
提示:所对应的函数y=f(x)在区间(1,2)上的图象是连续不断的一条曲线并且f(1)·f(2)<0.
2.典例2中是否可按照用二分法求函数零点近似值的步骤来求方程f(x)=0的近似解?
提示:可以按照用二分法求函数零点近似值的步骤来求方程f(x)=0的近似解.【解析】1.选B.因为f(1.25)·f(1.5)<0,所以方程的根落在区间(1.25,1.5).2.原方程即ln(2x+6)-3x+2=0.
令f(x)=ln(2x+6)-3x+2,
用计算器求得f(1)=1.0794,f(2)=-4.6974可知零点在(1,2)内,取区间中点x1=1.5,且f(1.5)≈-1.00,从而,可知零点在(1,1.5)内;再取区间中点x2=1.25,且f(1.25)≈0.20,从而,可知零点在(1.25,1.5)内;同理取区间中点x3=1.375,且f(1.375)<0,从而,可知零点在(1.25,1.375)内;由于|6.75-6.812 5|=0.125<0.2,故函数的零点可取为1.375.
即方程ln(2x+6)+2=3x在区间(1,2)内的近似解可取为1.375.【方法技巧】用二分法求方程的近似解的思路和方法
(1)思路:根据函数的零点与相应方程解的关系,求函数的零点与求相应方程的解是等价的.所以求方程f(x)=0的近似解,可按照用二分法求函数零点近似值的步骤求解.
(2)方法:对于求形如f(x)=g(x)的方程的近似解,可以通过移项转化成求函数F(x)=f(x)-g(x)的零点的近似解,然后按照用二分法求函数零点的近似值的步骤求解.【变式训练】用“二分法”求方程log x+x-4=0在区间[4,8]内的实
根,取区间中点为x0=6.那么下一个有根的区间是 .【解析】令f(x)=log x+x-4,
由f(4)=log 4+4-4=-2<0,
f(6)=log 6+6-4=2+log 6,
因为6>4,所以log 6故f(6)=2+log 6<0,
f(8)=log 8+8-4=4-3=1>0,
得到下一个有根的区间应为(6,8).
答案:(6,8)【补偿训练】方程x3-3=0在区间[1,2]内的近似解是 (精确度0.1).
【解析】设f(x)=x3-3,由于f(1)=-2<0,f(2)=5>0,
因此函数f(x)=x3-3在区间[1,2]内有零点,用二分法逐次计算,列表如下:因为|1.5-1.437 5|=0.062 5<0.1,因此方程x3-3=0在区间[1,2]内的近似解可取为1.5或1.437 5.
答案:1.5或1.437 5 易错案例 用二分法来确定函数零点所在的区间
【典例】已知函数f(x)在区间(0,a)上有唯一的零点(a>0),在用二
分法寻找零点的过程中,以此确定了零点所在的区间为
则下列说法中正确的是( )A.函数f(x)在区间 内一定有零点
B.函数f(x)在区间 或 内有零点
C.函数f(x)在区间 内无零点
D.函数f(x)在区间 或 内有零点,或零点是【失误案例】【错解分析】分析以上的解析过程,你知道错在哪儿吗?
提示:错误的根本原因是忘记端点 也可能为零点,从而错选B.【自我矫正】选D.根据二分法原理,依次“二分”区间后,零点应存
在于更小的区间,因此零点应存在区间【防范措施】
1.明确二分法的求解原理
二分法是不断把区间一分为二逐渐逼近零点的方法.有时中点值会恰
好为函数的零点.如本例中“ =0”有可能成立.
2.要把握好区间的取舍
区间每次一分为二,均可把原区间的长度减半,从而保留端点处函数
值异号的区间,而该区间在检验之前并不知道舍弃哪个区间.如本例
中在检验之前并不知道区间 哪一个会被舍弃.
用二分法求方程的近似解【知识提炼】
1.二分法的定义
(1)满足的条件:
在区间[a,b]上_________的函数y=f(x)且在区间端点的函数值满足:
_____________.连续不断f(a)·f(b)<0(2)操作过程:
把函数f(x)的零点所在的区间_________,使区间的两个端点逐步逼
近_____,进而得到零点的近似值. 一分为二零点2.二分法求函数零点近似值的步骤f(a)·f(b)<0f(c)=0b=cf(c)·f(b)<0(a,c)(c,b)|a-b|<ε【即时小测】
1.思考下列问题
(1)所有函数的零点都能用二分法求其所在的区间吗?
提示:不是所有的函数都能用二分法来判断零点所在的区间.只有图象在给定区间上是连续不断的,且在区间的端点处的函数值是异号的函数,才可以用二分法求函数的零点所在的区间.(2)用二分法求方程的近似解时,如何决定步骤的结束?
提示:看清题目的精确度,当零点所在区间的两个端点值之差的绝对值小于精确度时,则二分法步骤结束. 2.下列函数不宜用二分法求零点的是 ( )
A.f(x)=x3-2 B.f(x)=lnx-3
C.f(x)=x2+2 x+2 D.f(x)=-x2+4x-1
【解析】选C.因为f(x)=x2+2 x+2=(x+ )2≥0,即含有零点的区间
[a,b]不满足f(a)·f(b)<0.3.用二分法求函数f(x)=x3+5的零点可以选取的初始区间是 ( )
A.[-2,1] B.[-1,0]
C.[0,1] D.[1,2]
【解析】选A.由于f(-2)=(-2)3+5=-3<0,f(1)=1+5=6>0,所以可选取
[-2,1]作为初始区间.4.已知二次函数f(x)=x2-x-6在区间[1,4]上的图象是一条连续的曲线,且f(1)=-6<0,f(4)=6>0,由零点存在性定理可知函数在[1,4]内有零点,用二分法求解时,取(1,4)的中点a,则f(a)= .
【解析】由于(1,4)的中点a= ,则
答案:-2.255.在用二分法求方程f(x)=0在区间[0,1]上的近似解时,经计算,f(0.425)>0,f(0.552)>0,f(0.605)<0,即得到方程的一个近似解为 .(精确度为0.1)
【解析】因为|0.605-0.552|=0.053<0.1,
所以可取0.605或0.552作为方程f(x)=0的一个近似解.
答案:0.605或0.552【知识探究】
知识点 二分法的概念及利用其求函数零点的近似值
观察图形,回答下列问题:
问题1:上图中的线路出现故障,你能否设计一个维修方案来迅速查出故障所在?
问题2:利用二分法求函数零点时应把握哪几个关键点?【总结提升】
1.理解二分法的含义时要注意的两点
(1)二分法是求函数零点近似值的一种方法,根据题目要求的精确度,只需进行有限次运算即可.
(2)它的根据是根的存在性定理.
2.二分法求函数零点的两个关键点
(1)初始区间的选取,符合条件(包括零点),又要使其长度尽量小.
(2)进行精确度的判断,以决定是停止计算还是继续计算.【题型探究】
类型一 二分法概念的理解
【典例】1.(2015·昌平高一检测)关于“二分法”求方程的近似
解,说法正确的是 ( )
A.“二分法”求方程的近似解一定可将y=f(x)在[a,b]内的所有零
点得到
B.“二分法”求方程的近似解有可能得不到y=f(x)在[a,b]内的零点
C.应用“二分法”求方程的近似解,y=f(x)在[a,b]内有可能无零点
D.“二分法”求方程的近似解可能得到f(x)=0在[a,b]内的精确解2.通过下列函数的图象,判断能用“二分法”求其零点的是 ( )【解题探究】1.二分法的实质是什么?
提示:二分法就是通过不断选取区间的中点,将所选区间一分为二,逐步逼近,从而获得零点的近似值.2.典例2中能用“二分法”求零点的函数图象有什么特征?
提示:其特征为:图象经过x轴,且与x轴交点处两侧的函数值符号相反.【解析】1.选D.二分法求零点,则一定有且能求出,故B,C不正确;零点左侧与右侧的函数值符号相同的零点不能用二分法得到,故A不正确,故选D.
2.选C.在A中,函数无零点.在B和D中,函数有零点,但它们在零点左右的函数值符号相同,因此它们都不能用二分法来求零点.而在C中,函数图象是连续不断的,且图象与x轴有交点,并且在交点处两侧的函数值符号相反,所以C中的函数能用二分法求其零点.【方法技巧】运用二分法求函数的零点应具备的条件
(1)函数图象在零点附近连续不断.
(2)在该零点左右函数值异号.
只有满足上述两个条件,才可用二分法求函数零点.【变式训练】用“二分法”可求近似解,对于精确度ε说法正确的
是 ( )
A.ε越大,零点的精确度越高
B.ε越大,零点的精确度越低
C.重复计算次数就是ε
D.重复计算次数与ε无关
【解析】选B.精确度ε决定计算的次数,其直接影响零点的精确度,ε越大,零点的精确度越低,ε越小,零点的精确度越高.类型二 用二分法求函数的零点
【典例】(2015·塘沽高一检测)求函数f(x)=x3-3x2-9x+1的一个负零点(精确度0.01).
【解题探究】典例中应先怎样判断负零点所在的区间?
提示:可借助零点的判断方法确定出负零点所在的区间,再利用二分法逐步确定.【解析】确定一个包含负数零点的区间(m,n),且f(m)·f(n)<0.因为f(-1)>0,f(-2)<0,
所以可以取区间(-2,-1)作为计算的初始区间,
当然选取再较大的区间也可以.用二分法逐次计算,列表如下:由于|-1.929 687 5+1.937 5|=0.007 812 5<0.01,所以函数的一个负零点近似值可取为-1.929 687 5.【延伸探究】
1.(变换条件)若本例改为“试判断函数f(x)=x3-3x2-9x+1在[-2,-1]
内有无零点,如果有,求出一个近似零点(精确度0.1)”又如何求解呢?【解析】因为f(-1)>0,f(-2)<0,且函数f(x)=x3-3x2-9x+1的图象是连续的曲线,根据函数零点的存在性定理可知,它在区间[-2,-1]内有零点,用二分法逐步计算,列表如下:由于|-1.875+1.937 5|=0.062 5<0.1,所以函数在区间[-2,-1]内的一个近似零点可取为-1.937 5.2.(变换条件、改变问法)若将函数改为“f(x)=x3+2x2-3x-6”,如何求该函数的正数零点?(精确度0.1)
【解析】确定一个包含正数零点的区间(m,n),且f(m)·f(n)<0.
因为f(0)=-6<0,f(1)=-6<0,f(2)=4>0,
所以可以取区间(1,2)作为计算的初始区间,
用二分法逐次计算,列表如下:由于|1.75-1.687 5|=0.062 5<0.1.所以函数的正数零点的近似值可取为1.687 5.【方法技巧】
1.用二分法求函数零点的近似值应遵循的原则
(1)需依据图象估计零点所在的初始区间[m,n](一般采用估计值的方法完成).
(2)取区间端点的中点c,计算f(c),确定有解区间是(m,c)还是(c,n),逐步缩小区间的“长度”,直到区间的两个端点符合精确度要求,终止计算,得到函数零点的近似值.2.二分法求函数零点步骤的记忆口诀
定区间,找中点;中值计算两边看.
同号丢,异号算,零点落在异号间.
重复做,何时止,精确度来把关口.【补偿训练】试确定函数f(x)= x+x-4零点的个数.
【解析】设y1= x,y2=4-x,则f(x)的零点个数即y1= x,y2=4-x的
图象的交点个数,
作出两函数大致图象,如图:由图知y1= x与y2=4-x的图象有两个交点,其中一个交点横坐标在区间(0,1)之内,另一个大于4.
因此函数f(x)= x+x-4零点的个数有两个.【延伸探究】
1.(改变问法)若本题条件不变,试求出其中最大零点的近似值.(精确
度0.1)
【解析】设y1= x,y2=4-x,则f(x)的零点个数即y1= x,y2=4-x的
图象的交点个数,
作出两函数大致图象,如图:由图知y1= x与y2=4-x的图象有两个交点,其中一个交点横坐标在
区间(0,1)之内,另一个大于4.
因为f(6)= 6+6-4= 6+2< 4+2=0,
f(7)= 7+7-4= 7+3> 8+3=0,
结合图象可知,另一个交点的横坐标在区间(6,7)之内,
综上分析知,函数f(x)= x+x-4在区间(6,7)内有最大零点x0,取区
间(6,7)的中点x1=6.5,用计算器算得f(6.5)≈-0.200,
因为f(6.5)·f(7)<0,
所以x0∈(6.5,7),
再取区间(6.5,7)的中点x2=6.75,
用计算器算得f(6.75)≈-0.005,
因为f(6.75)·f(7)<0,
所以x0∈(6.75,7).再取区间(6.75,7)的中点x3=6.875,
用计算器算得f(6.875)≈0.094,
因为f(6.75)·f(6.875)<0,
所以x0∈(6.75,6.875).再取区间(6.75,6.875)的中点x4=6.8125,用计算器算得f(6.8125)≈0.443,
因为f(6.8125)·f(6.75)<0,
所以x0∈(6.75,6.8125)由于|6.75-6.8125|=0.0625<0.1,
所以函数f(x)= x+x-4最大零点的近似值可取6.8125.2.(变换条件)将函数改为“f(x)=log2x+x-4”,试判断函数零点个数;并求零点的近似值.(精确度0.1)
【解析】设y1=log2x,y2=4-x,则f(x)的零点个数即y1=log2x,y2=4-x的图象的交点个数.
作出两函数的大致图象,如图:由图知,y1=log2x与y2=4-x的图象只有一个交点,
因为f(2)=log22+2-4=-1<0,
f(3)=log23+3-4=log23-1>log22-1=0,
所以函数f(x)=log2x+x-4只有一个零点,在区间(2,3)内.
取区间(2,3)的中点x1=2.5,
用计算器算得f(2.5)≈-0.178,
因为f(2.5)·f(3)<0,所以x0∈(2.5,3).再取区间(2.5,3)的中点x2=2.75,
用计算器算得f(2.75)≈0.209,
因为f(2.5)·f(2.75)<0,所以x0∈(2.5,2.75).
再取区间(2.5,2.75)的中点x3=2.625,
用计算器算得f(2.625)≈0.017,
因为f(2.5)·f(2.625)<0,所以x0∈(2.5,2.625).
再取区间(2.5,2.625)的中点x4=2.5625,用计算器算得f(2.5625)≈-0.080,
因为f(2.5625)·f(2.625)>0,所以x0∈(2.5625,2.625).
由于|2.625-2.5625|=0.0625<0.1,
所以函数f(x)=log2x+x-4零点的近似值可取2.5625.类型三 用二分法求方程的近似解
【典例】1.(2015·包头高一检测)设f(x)=3x+3x-8,用二分法求方程3x+3x-8=0在x∈(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,
f(1.25)<0,则方程的根落在区间( )
A.(1,1.25) B.(1.25,1.5)
C.(1.5,2) D.不能确定
2.借助计算器,用二分法求出方程ln(2x+6)+2=3x在区间(1,2)内的近似解(精确度0.2).【解题探究】1.典例1中方程3x+3x-8=0在x∈(1,2)内有解应具备什么条件?
提示:所对应的函数y=f(x)在区间(1,2)上的图象是连续不断的一条曲线并且f(1)·f(2)<0.
2.典例2中是否可按照用二分法求函数零点近似值的步骤来求方程f(x)=0的近似解?
提示:可以按照用二分法求函数零点近似值的步骤来求方程f(x)=0的近似解.【解析】1.选B.因为f(1.25)·f(1.5)<0,所以方程的根落在区间(1.25,1.5).2.原方程即ln(2x+6)-3x+2=0.
令f(x)=ln(2x+6)-3x+2,
用计算器求得f(1)=1.0794,f(2)=-4.6974可知零点在(1,2)内,取区间中点x1=1.5,且f(1.5)≈-1.00,从而,可知零点在(1,1.5)内;再取区间中点x2=1.25,且f(1.25)≈0.20,从而,可知零点在(1.25,1.5)内;同理取区间中点x3=1.375,且f(1.375)<0,从而,可知零点在(1.25,1.375)内;由于|6.75-6.812 5|=0.125<0.2,故函数的零点可取为1.375.
即方程ln(2x+6)+2=3x在区间(1,2)内的近似解可取为1.375.【方法技巧】用二分法求方程的近似解的思路和方法
(1)思路:根据函数的零点与相应方程解的关系,求函数的零点与求相应方程的解是等价的.所以求方程f(x)=0的近似解,可按照用二分法求函数零点近似值的步骤求解.
(2)方法:对于求形如f(x)=g(x)的方程的近似解,可以通过移项转化成求函数F(x)=f(x)-g(x)的零点的近似解,然后按照用二分法求函数零点的近似值的步骤求解.【变式训练】用“二分法”求方程log x+x-4=0在区间[4,8]内的实
根,取区间中点为x0=6.那么下一个有根的区间是 .【解析】令f(x)=log x+x-4,
由f(4)=log 4+4-4=-2<0,
f(6)=log 6+6-4=2+log 6,
因为6>4,所以log 6
f(8)=log 8+8-4=4-3=1>0,
得到下一个有根的区间应为(6,8).
答案:(6,8)【补偿训练】方程x3-3=0在区间[1,2]内的近似解是 (精确度0.1).
【解析】设f(x)=x3-3,由于f(1)=-2<0,f(2)=5>0,
因此函数f(x)=x3-3在区间[1,2]内有零点,用二分法逐次计算,列表如下:因为|1.5-1.437 5|=0.062 5<0.1,因此方程x3-3=0在区间[1,2]内的近似解可取为1.5或1.437 5.
答案:1.5或1.437 5 易错案例 用二分法来确定函数零点所在的区间
【典例】已知函数f(x)在区间(0,a)上有唯一的零点(a>0),在用二
分法寻找零点的过程中,以此确定了零点所在的区间为
则下列说法中正确的是( )A.函数f(x)在区间 内一定有零点
B.函数f(x)在区间 或 内有零点
C.函数f(x)在区间 内无零点
D.函数f(x)在区间 或 内有零点,或零点是【失误案例】【错解分析】分析以上的解析过程,你知道错在哪儿吗?
提示:错误的根本原因是忘记端点 也可能为零点,从而错选B.【自我矫正】选D.根据二分法原理,依次“二分”区间后,零点应存
在于更小的区间,因此零点应存在区间【防范措施】
1.明确二分法的求解原理
二分法是不断把区间一分为二逐渐逼近零点的方法.有时中点值会恰
好为函数的零点.如本例中“ =0”有可能成立.
2.要把握好区间的取舍
区间每次一分为二,均可把原区间的长度减半,从而保留端点处函数
值异号的区间,而该区间在检验之前并不知道舍弃哪个区间.如本例
中在检验之前并不知道区间 哪一个会被舍弃.
