第5章 相交线与平行线 达标检测卷
文档属性
| 名称 | 第5章 相交线与平行线 达标检测卷 |  | |
| 格式 | zip | ||
| 文件大小 | 230.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-07-25 10:39:55 | ||
图片预览


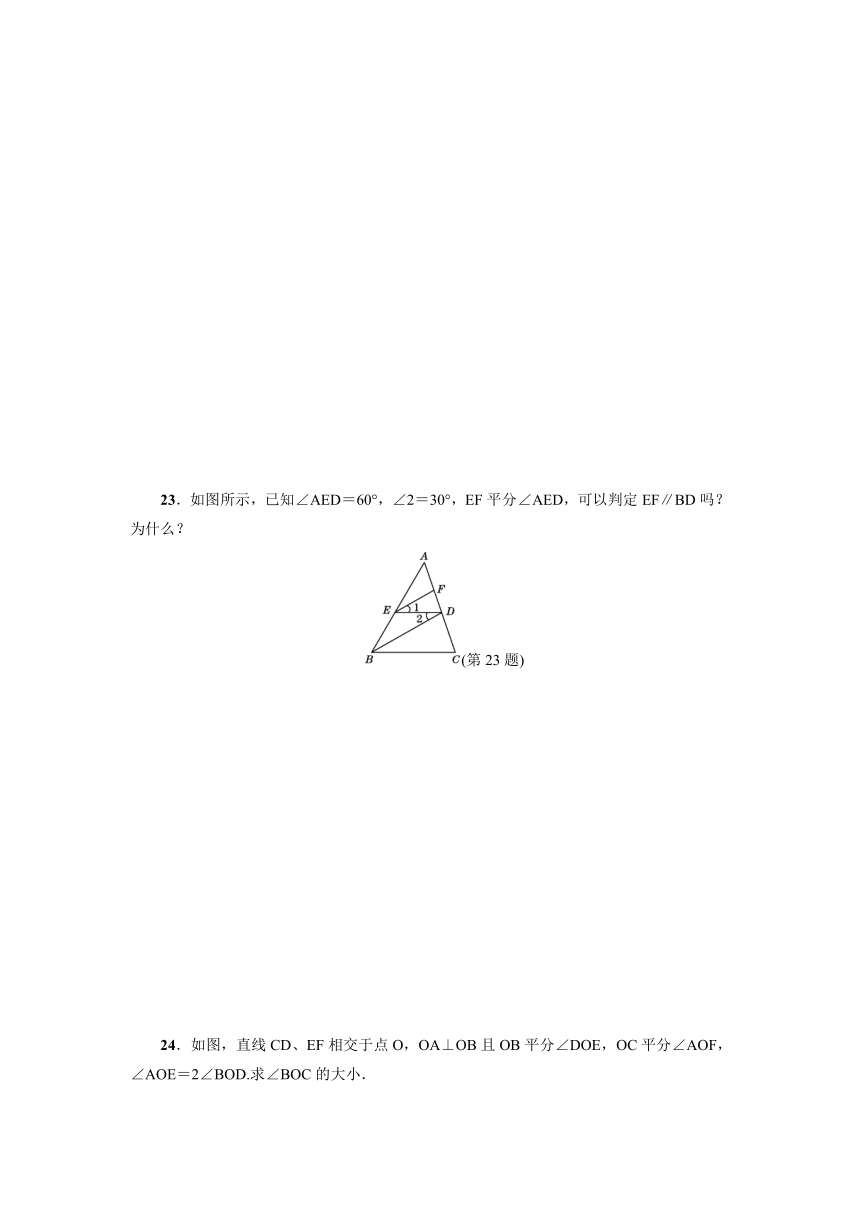
文档简介
第5章
相交线与平行线
达标检测卷
(120分,90分钟)
题 号
一
二
三
总 分
得 分
一、选择题(每题3分,共30分)
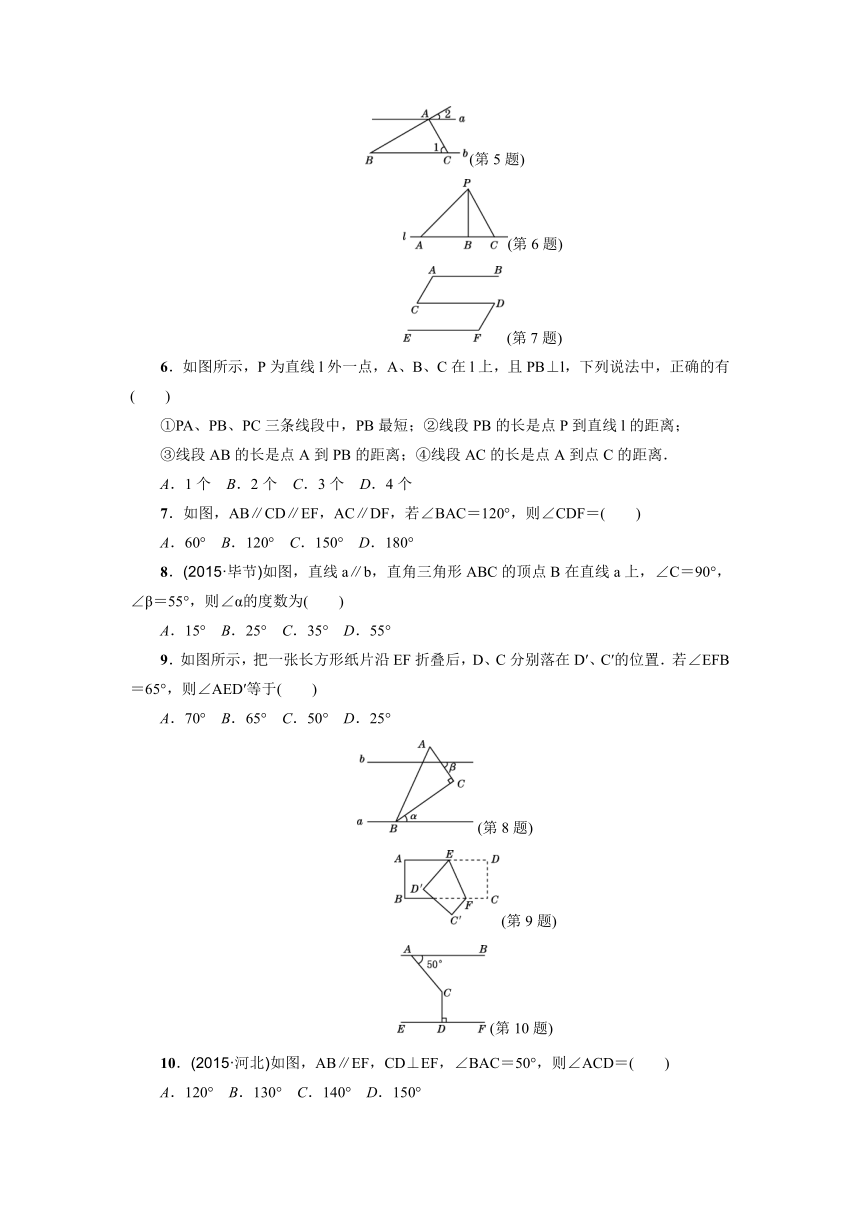
1.下列选项中,两个角是对顶角的是( )
2.如图所示,三条直线l1,l2,l3相交于点E,则∠1+∠2+∠3等于( )
A.90°
B.120°
C.180°
D.360°
(第2题)
(第3题)
(第4题)
3.如图所示,下列说法正确的是( )
A.∠1和∠4不是同位角
B.∠2与∠4是同位角
C.∠2和∠4是内错角
D.∠3和∠4是同旁内角
4.如图,在5×5方格纸中将图①中的图形N平移到图②所示的位置,那么下列平移正确的是( )
A.先向下平移1格,再向左平移1格
B.先向下平移1格,再向左平移2格
C.先向下平移2格,再向左平移1格
D.先向下平移2格,再向左平移2格
5.(2014·丽水)如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠1=60°,则∠2的度数是( )
A.50°
B.45°
C.35°
D.30°
(第5题)
(第6题)
(第7题)
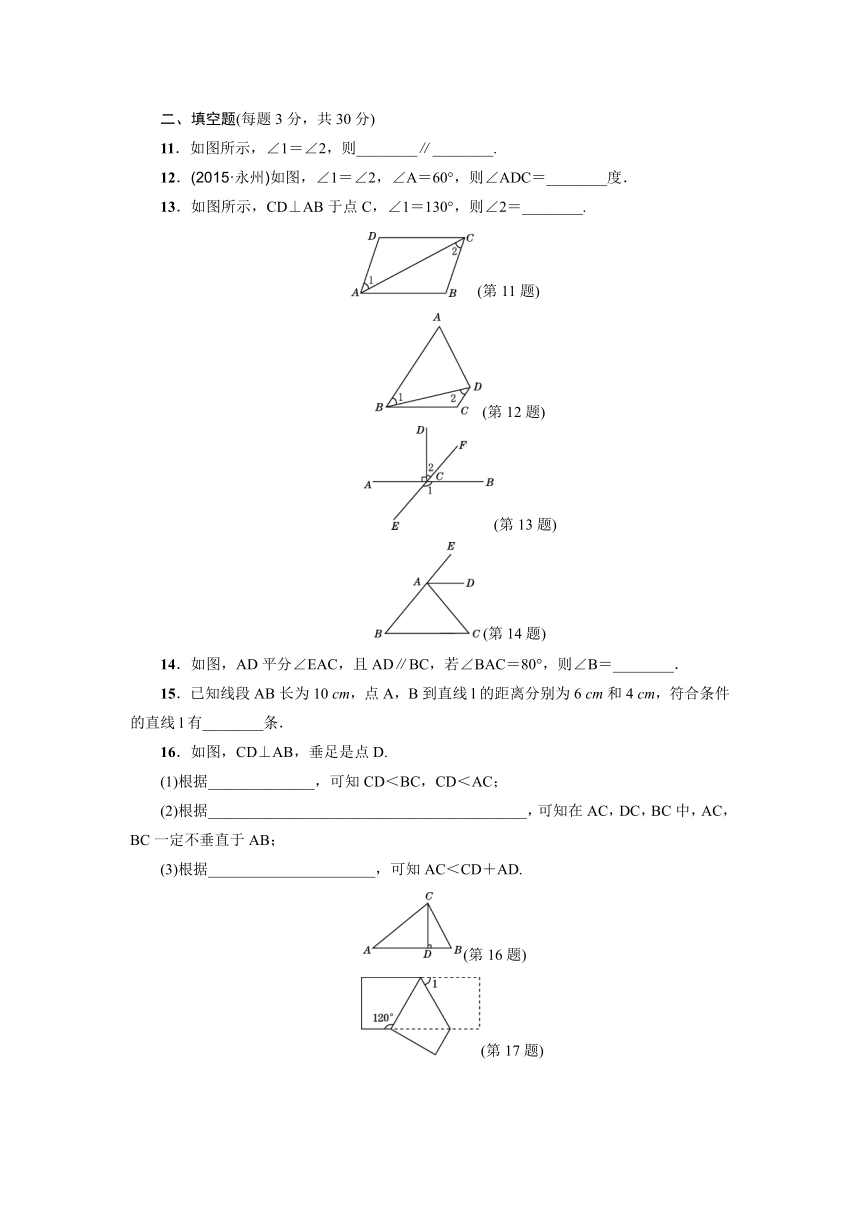
6.如图所示,P为直线l外一点,A、B、C在l上,且PB⊥l,下列说法中,正确的有( )
①PA、PB、PC三条线段中,PB最短;②线段PB的长是点P到直线l的距离;
③线段AB的长是点A到PB的距离;④线段AC的长是点A到点C的距离.
A.1个
B.2个
C.3个
D.4个
7.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=( )
A.60°
B.120°
C.150°
D.180°
8.(2015·毕节)如图,直线a∥b,直角三角形ABC的顶点B在直线a上,∠C=90°,∠β=55°,则∠α的度数为( )
A.15°
B.25°
C.35°
D.55°
9.如图所示,把一张长方形纸片沿EF折叠后,D、C分别落在D′、C′的位置.若∠EFB=65°,则∠AED′等于( )
A.70°
B.65°
C.50°
D.25°
(第8题)
(第9题)
(第10题)
10.(2015·河北)如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=( )
A.120°
B.130°
C.140°
D.150°
二、填空题(每题3分,共30分)
11.如图所示,∠1=∠2,则________∥________.
12.(2015·永州)如图,∠1=∠2,∠A=60°,则∠ADC=________度.
13.如图所示,CD⊥AB于点C,∠1=130°,则∠2=________.
(第11题)
(第12题)
(第13题)
(第14题)
14.如图,AD平分∠EAC,且AD∥BC,若∠BAC=80°,则∠B=________.
15.已知线段AB长为10
cm,点A,B到直线l的距离分别为6
cm和4
cm,符合条件的直线l有________条.
16.如图,CD⊥AB,垂足是点D.
(1)根据______________,可知CD<BC,CD<AC;
(2)根据__________________________________________,可知在AC,DC,BC中,AC,BC一定不垂直于AB;
(3)根据______________________,可知AC<CD+AD.
(第16题)
(第17题)
(第18题)
(第19题)
(第20题)
17.如图,将一张长方形纸条按图中折法折叠,根据图中所给的数据,可得∠1=________.
18.如图,将一块含有60°角的直角三角板的两个顶点放在长方形的对边上.如果∠1=18°,那么∠2的度数是________.
19.(2015·泰州)如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=________.
20.如图所示,弯形管道ABCD的一个拐角∠ABC=123°,那么另一个拐角∠BCD=________时,才能使管道AB与管道CD平行.
三、解答题(21题8分,22~25题每题10分,26题12分,共60分)
(第21题)
21.根据解答过程填空:如图,已知∠DAF=∠F,∠B=∠D,那么AB与DC平行吗?
解:∵∠DAF=∠F(____________),
∴________∥________(______________),
∴∠D=∠DCF(______________).
∵∠B=∠D(____________),
∴∠________=∠DCF(等量代换),∴AB∥DC(______________).
22.如图,M,N为坐落于公路两旁的村庄,如果一辆施工的机动车由A向B行驶,产生的噪音会对两个村庄造成影响.
(1)当施工车行驶到何处时,产生的噪音分别对两村庄影响最大?在图中标出来.
(2)当施工车由A向B行驶时,产生的噪音对M,N两村庄的影响情况如何?
(第22题)
23.如图所示,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判定EF∥BD吗?为什么?
(第23题)
24.如图,直线CD、EF相交于点O,OA⊥OB且OB平分∠DOE,OC平分∠AOF,∠AOE=2∠BOD.求∠BOC的大小.
(第24题)
25.如图,直线AB⊥CD于O,DH交EF于G.若AB∥EF,∠CDH=135°,求∠FGH的度数.
(第25题)
26.如图a①,AB∥CD,猜想∠BPD与∠B、∠D的关系,并说明理由.
(第26题)
(1)填空:
解:猜想∠BPD+∠B+∠D=360°.
理由:过点P作EF∥AB,如图b所示,
∴∠B+∠BPE=180°(①________________).
∵AB∥CD,EF∥AB,
∴EF∥CD(如果两条直线都和第三条直线平行,那么②________________),
∴∠EPD+∠D=180°(③________________).
∴∠B+∠BPE+∠EPD+∠D=④________,
即∠B+∠BPD+∠D=360°.
(2)仿照上面的解题方法,观察图a②,已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.
(3)观察图a③和a④,已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,不需要说明理由.
答案
一、1.C 2.C 3.D 4.C 5.D 6.D
7.A 解析:∵AB∥CD,∴∠A+∠C=180°,∴∠C=180°-120°=60°.又∵AC∥DF,∴∠C=∠D=60°.故选A.
8.C
9.C 解析:因为AD∥BC,所以∠DEF
( http: / / www.21cnjy.com )=∠EFB=65°,所以∠D′EF=∠DEF=65°,所以∠AED′=180°-65°×2=50°.
10.C
二、11.AD BC 12.120 13.40° 14.50°
15.3 解析:如图.
(第15题)
16.(1)垂线段最短 (2)在同一平面内,过一点有且只有一条直线与已知直线垂直
(3)两点之间,线段最短 解析:(3)题答案不唯一.
17.60° 解析:如图,因为长方形的对边
( http: / / www.21cnjy.com )平行,所以∠2+120°=180°,所以∠2=180°-120°=60°.根据折叠可知∠1=∠3,所以∠1=(180°-∠2)÷2=(180°-60°)÷2=60°.
(第17题)
18.12° 19.140° 20.57°
三、21.解:已知 AD BF 内错角相等,两直线平行 两直线平行,内错角相等 已知 B 同位角相等,两直线平行.
22.解:(1)过点M,N
( http: / / www.21cnjy.com )分别作AB的垂线,设垂足分别为P,Q,则当施工车行驶到点P,Q处时产生的噪音分别对M,N两村庄影响最大,如图所示.
(第22题)
(2)由A至P时,产生的噪音对两村庄的
( http: / / www.21cnjy.com )影响越来越大,到P处时,对M村庄的影响最大;由P至Q时,对M村庄的影响越来越小,对N村庄的影响越来越大,到Q处时,对N村庄的影响最大;由Q至B时,对M,N两村庄的影响越来越小.
解析:本题运用了建模思想,即灵活运用数学知识解决实际问题,此题运用垂线段最短的知识解题.
23.解:可以判定EF∥BD.理由:
因为EF平分∠AED(已知),
所以∠1=∠AED(角平分线的定义).
因为∠AED=60°(已知).
所以∠1=30°.
因为∠2=30°(已知),所以∠1=∠2,
所以EF∥BD(内错角相等,两直线平行).
24.解:∵OA⊥OB,∴∠AOB
( http: / / www.21cnjy.com )=90°,又∠AOE=2∠BOD且OB平分∠DOE.∴∠AOE=2∠BOE,∴∠AOE=60°,∠BOE=30°,∠AOF=120°.∵OC平分∠AOF,∴∠AOC=∠AOF=×120°=60°.∴∠BOC=∠BOE+∠AOE+∠AOC=30°+60°+60°=150°.
25.解:如图,过D作MN∥AB,∵AB∥EF,∴MN∥EF.
则∠FGH=∠MDH.∵CD⊥AB,∴∠COB=90°,
∵AB∥MN,∴∠CDM=∠COB=90°,
∴∠MDH=∠CDH-∠CDM=135°-90°=45°,
∴∠FGH=45°.
(第25题)
(第26题)
26.解:(1)①两直线平行,同旁内角互补 ②这两条直线也互相平行
③两直线平行,同旁内角互补 ④360°.
(2)猜想∠BPD=∠B+∠D.
理由:过点P作EF∥AB,如图所示,
∴∠B=∠BPF(两直线平行,内错角相等).
∵AB∥CD,AB∥EF,
∴EF∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠D=∠DPF(两直线平行,内错角相等).
∴∠B+∠D=∠BPF+∠DPF=∠BPD.
即∠BPD=∠B+∠D.
(3)题图a③中∠BPD=∠D-∠B,题图a④中∠BPD=∠B-∠D.(提示:过点P作EF∥AB,利用平行线的性质可以说明)
相交线与平行线
达标检测卷
(120分,90分钟)
题 号
一
二
三
总 分
得 分
一、选择题(每题3分,共30分)
1.下列选项中,两个角是对顶角的是( )
2.如图所示,三条直线l1,l2,l3相交于点E,则∠1+∠2+∠3等于( )
A.90°
B.120°
C.180°
D.360°
(第2题)
(第3题)
(第4题)
3.如图所示,下列说法正确的是( )
A.∠1和∠4不是同位角
B.∠2与∠4是同位角
C.∠2和∠4是内错角
D.∠3和∠4是同旁内角
4.如图,在5×5方格纸中将图①中的图形N平移到图②所示的位置,那么下列平移正确的是( )
A.先向下平移1格,再向左平移1格
B.先向下平移1格,再向左平移2格
C.先向下平移2格,再向左平移1格
D.先向下平移2格,再向左平移2格
5.(2014·丽水)如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠1=60°,则∠2的度数是( )
A.50°
B.45°
C.35°
D.30°
(第5题)
(第6题)
(第7题)
6.如图所示,P为直线l外一点,A、B、C在l上,且PB⊥l,下列说法中,正确的有( )
①PA、PB、PC三条线段中,PB最短;②线段PB的长是点P到直线l的距离;
③线段AB的长是点A到PB的距离;④线段AC的长是点A到点C的距离.
A.1个
B.2个
C.3个
D.4个
7.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=( )
A.60°
B.120°
C.150°
D.180°
8.(2015·毕节)如图,直线a∥b,直角三角形ABC的顶点B在直线a上,∠C=90°,∠β=55°,则∠α的度数为( )
A.15°
B.25°
C.35°
D.55°
9.如图所示,把一张长方形纸片沿EF折叠后,D、C分别落在D′、C′的位置.若∠EFB=65°,则∠AED′等于( )
A.70°
B.65°
C.50°
D.25°
(第8题)
(第9题)
(第10题)
10.(2015·河北)如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=( )
A.120°
B.130°
C.140°
D.150°
二、填空题(每题3分,共30分)
11.如图所示,∠1=∠2,则________∥________.
12.(2015·永州)如图,∠1=∠2,∠A=60°,则∠ADC=________度.
13.如图所示,CD⊥AB于点C,∠1=130°,则∠2=________.
(第11题)
(第12题)
(第13题)
(第14题)
14.如图,AD平分∠EAC,且AD∥BC,若∠BAC=80°,则∠B=________.
15.已知线段AB长为10
cm,点A,B到直线l的距离分别为6
cm和4
cm,符合条件的直线l有________条.
16.如图,CD⊥AB,垂足是点D.
(1)根据______________,可知CD<BC,CD<AC;
(2)根据__________________________________________,可知在AC,DC,BC中,AC,BC一定不垂直于AB;
(3)根据______________________,可知AC<CD+AD.
(第16题)
(第17题)
(第18题)
(第19题)
(第20题)
17.如图,将一张长方形纸条按图中折法折叠,根据图中所给的数据,可得∠1=________.
18.如图,将一块含有60°角的直角三角板的两个顶点放在长方形的对边上.如果∠1=18°,那么∠2的度数是________.
19.(2015·泰州)如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=________.
20.如图所示,弯形管道ABCD的一个拐角∠ABC=123°,那么另一个拐角∠BCD=________时,才能使管道AB与管道CD平行.
三、解答题(21题8分,22~25题每题10分,26题12分,共60分)
(第21题)
21.根据解答过程填空:如图,已知∠DAF=∠F,∠B=∠D,那么AB与DC平行吗?
解:∵∠DAF=∠F(____________),
∴________∥________(______________),
∴∠D=∠DCF(______________).
∵∠B=∠D(____________),
∴∠________=∠DCF(等量代换),∴AB∥DC(______________).
22.如图,M,N为坐落于公路两旁的村庄,如果一辆施工的机动车由A向B行驶,产生的噪音会对两个村庄造成影响.
(1)当施工车行驶到何处时,产生的噪音分别对两村庄影响最大?在图中标出来.
(2)当施工车由A向B行驶时,产生的噪音对M,N两村庄的影响情况如何?
(第22题)
23.如图所示,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判定EF∥BD吗?为什么?
(第23题)
24.如图,直线CD、EF相交于点O,OA⊥OB且OB平分∠DOE,OC平分∠AOF,∠AOE=2∠BOD.求∠BOC的大小.
(第24题)
25.如图,直线AB⊥CD于O,DH交EF于G.若AB∥EF,∠CDH=135°,求∠FGH的度数.
(第25题)
26.如图a①,AB∥CD,猜想∠BPD与∠B、∠D的关系,并说明理由.
(第26题)
(1)填空:
解:猜想∠BPD+∠B+∠D=360°.
理由:过点P作EF∥AB,如图b所示,
∴∠B+∠BPE=180°(①________________).
∵AB∥CD,EF∥AB,
∴EF∥CD(如果两条直线都和第三条直线平行,那么②________________),
∴∠EPD+∠D=180°(③________________).
∴∠B+∠BPE+∠EPD+∠D=④________,
即∠B+∠BPD+∠D=360°.
(2)仿照上面的解题方法,观察图a②,已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.
(3)观察图a③和a④,已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,不需要说明理由.
答案
一、1.C 2.C 3.D 4.C 5.D 6.D
7.A 解析:∵AB∥CD,∴∠A+∠C=180°,∴∠C=180°-120°=60°.又∵AC∥DF,∴∠C=∠D=60°.故选A.
8.C
9.C 解析:因为AD∥BC,所以∠DEF
( http: / / www.21cnjy.com )=∠EFB=65°,所以∠D′EF=∠DEF=65°,所以∠AED′=180°-65°×2=50°.
10.C
二、11.AD BC 12.120 13.40° 14.50°
15.3 解析:如图.
(第15题)
16.(1)垂线段最短 (2)在同一平面内,过一点有且只有一条直线与已知直线垂直
(3)两点之间,线段最短 解析:(3)题答案不唯一.
17.60° 解析:如图,因为长方形的对边
( http: / / www.21cnjy.com )平行,所以∠2+120°=180°,所以∠2=180°-120°=60°.根据折叠可知∠1=∠3,所以∠1=(180°-∠2)÷2=(180°-60°)÷2=60°.
(第17题)
18.12° 19.140° 20.57°
三、21.解:已知 AD BF 内错角相等,两直线平行 两直线平行,内错角相等 已知 B 同位角相等,两直线平行.
22.解:(1)过点M,N
( http: / / www.21cnjy.com )分别作AB的垂线,设垂足分别为P,Q,则当施工车行驶到点P,Q处时产生的噪音分别对M,N两村庄影响最大,如图所示.
(第22题)
(2)由A至P时,产生的噪音对两村庄的
( http: / / www.21cnjy.com )影响越来越大,到P处时,对M村庄的影响最大;由P至Q时,对M村庄的影响越来越小,对N村庄的影响越来越大,到Q处时,对N村庄的影响最大;由Q至B时,对M,N两村庄的影响越来越小.
解析:本题运用了建模思想,即灵活运用数学知识解决实际问题,此题运用垂线段最短的知识解题.
23.解:可以判定EF∥BD.理由:
因为EF平分∠AED(已知),
所以∠1=∠AED(角平分线的定义).
因为∠AED=60°(已知).
所以∠1=30°.
因为∠2=30°(已知),所以∠1=∠2,
所以EF∥BD(内错角相等,两直线平行).
24.解:∵OA⊥OB,∴∠AOB
( http: / / www.21cnjy.com )=90°,又∠AOE=2∠BOD且OB平分∠DOE.∴∠AOE=2∠BOE,∴∠AOE=60°,∠BOE=30°,∠AOF=120°.∵OC平分∠AOF,∴∠AOC=∠AOF=×120°=60°.∴∠BOC=∠BOE+∠AOE+∠AOC=30°+60°+60°=150°.
25.解:如图,过D作MN∥AB,∵AB∥EF,∴MN∥EF.
则∠FGH=∠MDH.∵CD⊥AB,∴∠COB=90°,
∵AB∥MN,∴∠CDM=∠COB=90°,
∴∠MDH=∠CDH-∠CDM=135°-90°=45°,
∴∠FGH=45°.
(第25题)
(第26题)
26.解:(1)①两直线平行,同旁内角互补 ②这两条直线也互相平行
③两直线平行,同旁内角互补 ④360°.
(2)猜想∠BPD=∠B+∠D.
理由:过点P作EF∥AB,如图所示,
∴∠B=∠BPF(两直线平行,内错角相等).
∵AB∥CD,AB∥EF,
∴EF∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
∴∠D=∠DPF(两直线平行,内错角相等).
∴∠B+∠D=∠BPF+∠DPF=∠BPD.
即∠BPD=∠B+∠D.
(3)题图a③中∠BPD=∠D-∠B,题图a④中∠BPD=∠B-∠D.(提示:过点P作EF∥AB,利用平行线的性质可以说明)
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
