数学六年级下北师大版1.2圆柱的表面积说课课件(41张)
文档属性
| 名称 | 数学六年级下北师大版1.2圆柱的表面积说课课件(41张) |

|
|
| 格式 | zip | ||
| 文件大小 | 257.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-01 00:00:00 | ||
图片预览









文档简介
课件41张PPT。圆柱的表面积说 课 内 容 本课是北师大版六年级数学下册第一单元《圆柱和圆锥》中的内容,是小学数学《空间与图形》领域中最后一个单元的知识。是在学生学习了简单平面图形和长方体、正方体的表面积与体积的基础上进行教学的。学好这一部分内容,可以进一步发展学生的空间观念,为以后学习其它几何形体打下坚实的基础。 六年级的学生,经历了多种简单图形的面积推导过程,初步具备了用转化思想探究问题的能力。已经能够在教师提供素材的前提下,通过动手操作、观察发现,主动地探索新知,促进知识的迁移。不仅如此,课前我还让学生间互考有关圆的计算问题,提前扫清了用公式解决问题时的障碍。基于以上教材和学情分析,我制定了如下教学目标: 1.理解和掌握圆柱体侧面积和表面积的计算方法.
2.通过动手操作,建立空间观念,利用转化的思想探究问题。
3.培养学生的观察、操作、概括的能力以及利用知识灵活地解决实际问题的能力。
4.培养学生的合作学习和主动探求知识的学习品质。掌握圆柱表面积计算方法,并能解决生活中的简单问题。理解圆柱侧面展开图与圆柱的联系, 灵活的解决简单的实际问题根据本节课知识特点以及学生的认知规律,我综合运用动手操作亲身实践教学法、合作学习教学法、演示法等方法来实现教学目标。我也注重学法指导,学生采用动手操作、自 主探究,合作交流等学习方法,亲身经历做、找、说等活动,做到让学生学会并会学。
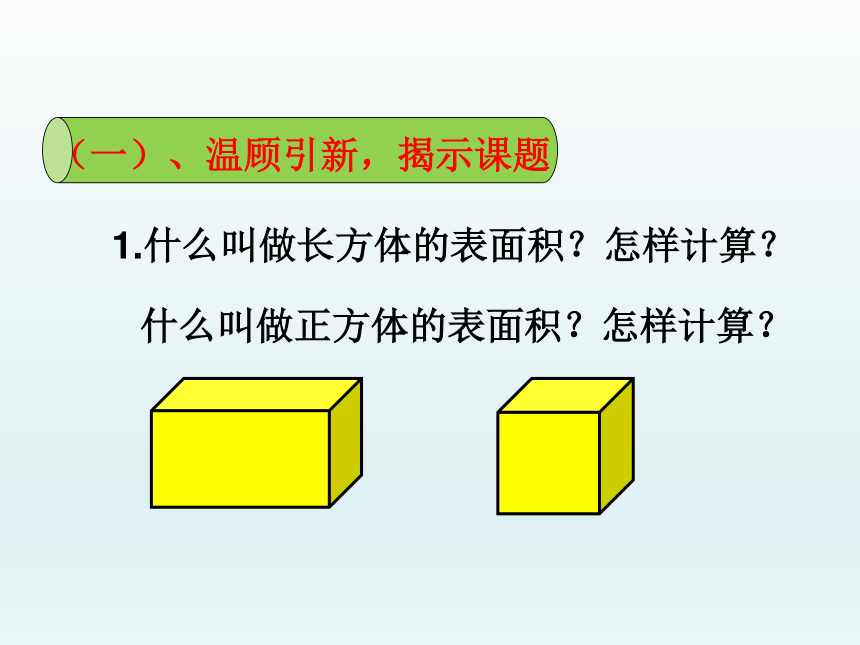
1.什么叫做长方体的表面积?怎样计算?什么叫做正方体的表面积?怎样计算?2.怎样计算圆的周长和面积?C = πdC = 2πr求周长:已知直径:已知半径:S=πr2S=π(C÷π÷2)2已知半径:已知直径:已知周长:S=π(d÷2)2求面积:本环节出示问题情境,学生抢答(各组长记录学生回答问题的情况,答对的计入小组成绩),充分利用知识的迁移性,学生在复习中回忆表面积的含义及圆的相关计算问题,为进一步探索圆柱的表面积作好准备。
圆柱的表面积=圆柱的侧面积+2×底面的面积设计意图:紧接着出示例3,揭示课题,并引导学生得出圆柱的表面积是侧面积加上两个底面面积。 圆柱的底面是两个相等的圆,对于圆的面积学生是很容易求解的,而圆柱的侧面却是个“曲面”,怎样才能求出这个“曲面”的面积就成了解决问题的关键。为此我设计下面的小组活动:活动1自制圆柱
(课前我给学生提供了我自制的学具袋:袋内有长方形,平行四边形,正方形,圆形若干。)
合作要求:四人合作,利用老师提供的学具,选择合适的材料制作一个圆柱。
(柱体部分的接缝可用胶条粘好,上下两个底直接搭在柱体上下就可以,不用粘上。)
在制作的过程中思考一个问题:
你们是如何选择材料的?你有什么发现? 在制作过程中,利用平行四边形做圆柱的侧面,学生不易想到,必要时老师要加以引导,把时间控制在4分钟以内。通过这个活动,把学生理解上的难点“由曲变直”,转化为“由直变曲”,更易于学生接受。并且直观感受曲面和平面之间的关系,有利于突破教学难点,同时提高了学生的学习兴趣,让学生在快乐的情绪下进行学习。活动2公式推导
创设问题情境,以问题引领思考。
合作要求:先独立思考,然后再在小组内交流,组长负责汇报总结。
问题1:把圆柱的侧面沿高线展开,找一找长方形和圆柱的联系。说一说,可以怎样求侧面的面积?
因为学生经历过平行四边形,三角形,圆等面积公式的探究活动。学优生会快速的得到结论,再通过互动学习,学差生也会豁然开朗,做到人人都有收获。我再借助电子白板展示动态效果,帮助学生更好的理解长方形的长就是底面圆的周长。学生汇报的好的要加以鼓励和表扬,并做记录。底面底面底面底面底面底面底面底面底面底面底面底面底面底面底面高底面圆柱的侧面积 + 2×底面的面积圆柱的表面积= S表 = ch + 2πr2问题3:如果给出的条件是底面半径和高,或者是底面直径和高,又该怎样算?问题2:用字母该怎样表示?紧接着出示问题2和问题3分别得到字母公式及其他两钟解法,并板书。活动3
与同桌间说一说自己的推导过程。
设计意图:这个环节一定要舍得花时间,让学生在交流中锻炼语言表达能力,争取让每一个学生都有自己的收获。 建构主义认为,真正的数学学习不是对于外部所授予知识的简单接受和积累,而是学生以自己已有的知识和经验为基础的主动建构过程。
在这一系列的探究过程中,学生的眼、手、脑等多种感官参与到感知活动中,探究的精神得到了张扬,自主学习的能力得到了实实在的落实。教学的重点、难点在学生的探究实践中得到了突破。1用一张长8cm、宽5 cm的长方形纸围成一个圆柱体,这个圆柱体的侧面积是( )cm2。基础练习 设计意图:这一环节是内化知识、训练思维、培养能力、形成技能的重要环节。我准备了6道题,共分为三个层次。2.现有三个圆柱,每个圆柱都有两个不同的条件, 求侧面积(只列算式,不计算):
①C=9.42厘米,h=5厘米。
②d=8米,h=3米。
③r=2分米,h=6分米(1)侧面积:(2)底面积:(3)表面积:2×3.14×2×4=50.24 (cm2)3.14×22=12.56 (cm2)50.24+12.56×2 =75.36(cm2)3.计算下面圆柱的表面积设计意图:基础练习,重在巩固新知识,加深对新知识的理解。1.猜一猜:联系生活实际,说说生活中的这些物品与哪些面的面积有关?
(1)圆形水池的占地面积;
(2)做一个无盖水桶所需铁皮的面积;
(3)做一个油桶所需铁皮的面积;
(4)求易拉罐上商标纸的面积;
(5)在水池的内壁和底面抹水泥,求抹水泥部分的面积
(6)往大厅的柱子上涂漆,求涂漆部分的面积; 综合练习2.一个圆柱,底面周长是23厘米,高是6厘米.求它的侧面积. 3.一顶圆柱形厨师帽,高28厘米,帽顶直径20厘米,做这样一顶帽子需要用多少面料(得数保留整十平方厘米)?
注意:这道题使用的材料要比计算得到的结果多一些。因此,这里不能用四舍五入法取近似值。而要用进一法取近似值。综合练习,从学生的最近区出发,选取生活中熟悉的物体,提高学生解决实际问题的能力,增强学生学好数学的信心,做到学以致用。挑战自我如果一段底面直径20厘米的圆柱形木头,截成两截,它的表面积会有什么变化呢?增加多少?设计意图:这道题是留给稍有余力的学生做的思考题。三个层次的习题安排,既可以让学差生够得着,又可以让学优生吃得饱,一堂课下来争取做到每个学生都有所发展。 谈一谈自己有什么收获吧?设计意图:借助此环节,可以反馈这堂课的教学效果,并加深学生对知识的理解。圆柱的表面积 = 侧面积 + 2×底面面积
S = ch + 2πr22πrπd设计意图:我的板书设计很简洁,这样既突出了重点,又给学生留下了深刻的印象。 我的说课内容到此为止,谢谢各位评委和老师!
2.通过动手操作,建立空间观念,利用转化的思想探究问题。
3.培养学生的观察、操作、概括的能力以及利用知识灵活地解决实际问题的能力。
4.培养学生的合作学习和主动探求知识的学习品质。掌握圆柱表面积计算方法,并能解决生活中的简单问题。理解圆柱侧面展开图与圆柱的联系, 灵活的解决简单的实际问题根据本节课知识特点以及学生的认知规律,我综合运用动手操作亲身实践教学法、合作学习教学法、演示法等方法来实现教学目标。我也注重学法指导,学生采用动手操作、自 主探究,合作交流等学习方法,亲身经历做、找、说等活动,做到让学生学会并会学。
1.什么叫做长方体的表面积?怎样计算?什么叫做正方体的表面积?怎样计算?2.怎样计算圆的周长和面积?C = πdC = 2πr求周长:已知直径:已知半径:S=πr2S=π(C÷π÷2)2已知半径:已知直径:已知周长:S=π(d÷2)2求面积:本环节出示问题情境,学生抢答(各组长记录学生回答问题的情况,答对的计入小组成绩),充分利用知识的迁移性,学生在复习中回忆表面积的含义及圆的相关计算问题,为进一步探索圆柱的表面积作好准备。
圆柱的表面积=圆柱的侧面积+2×底面的面积设计意图:紧接着出示例3,揭示课题,并引导学生得出圆柱的表面积是侧面积加上两个底面面积。 圆柱的底面是两个相等的圆,对于圆的面积学生是很容易求解的,而圆柱的侧面却是个“曲面”,怎样才能求出这个“曲面”的面积就成了解决问题的关键。为此我设计下面的小组活动:活动1自制圆柱
(课前我给学生提供了我自制的学具袋:袋内有长方形,平行四边形,正方形,圆形若干。)
合作要求:四人合作,利用老师提供的学具,选择合适的材料制作一个圆柱。
(柱体部分的接缝可用胶条粘好,上下两个底直接搭在柱体上下就可以,不用粘上。)
在制作的过程中思考一个问题:
你们是如何选择材料的?你有什么发现? 在制作过程中,利用平行四边形做圆柱的侧面,学生不易想到,必要时老师要加以引导,把时间控制在4分钟以内。通过这个活动,把学生理解上的难点“由曲变直”,转化为“由直变曲”,更易于学生接受。并且直观感受曲面和平面之间的关系,有利于突破教学难点,同时提高了学生的学习兴趣,让学生在快乐的情绪下进行学习。活动2公式推导
创设问题情境,以问题引领思考。
合作要求:先独立思考,然后再在小组内交流,组长负责汇报总结。
问题1:把圆柱的侧面沿高线展开,找一找长方形和圆柱的联系。说一说,可以怎样求侧面的面积?
因为学生经历过平行四边形,三角形,圆等面积公式的探究活动。学优生会快速的得到结论,再通过互动学习,学差生也会豁然开朗,做到人人都有收获。我再借助电子白板展示动态效果,帮助学生更好的理解长方形的长就是底面圆的周长。学生汇报的好的要加以鼓励和表扬,并做记录。底面底面底面底面底面底面底面底面底面底面底面底面底面底面底面高底面圆柱的侧面积 + 2×底面的面积圆柱的表面积= S表 = ch + 2πr2问题3:如果给出的条件是底面半径和高,或者是底面直径和高,又该怎样算?问题2:用字母该怎样表示?紧接着出示问题2和问题3分别得到字母公式及其他两钟解法,并板书。活动3
与同桌间说一说自己的推导过程。
设计意图:这个环节一定要舍得花时间,让学生在交流中锻炼语言表达能力,争取让每一个学生都有自己的收获。 建构主义认为,真正的数学学习不是对于外部所授予知识的简单接受和积累,而是学生以自己已有的知识和经验为基础的主动建构过程。
在这一系列的探究过程中,学生的眼、手、脑等多种感官参与到感知活动中,探究的精神得到了张扬,自主学习的能力得到了实实在的落实。教学的重点、难点在学生的探究实践中得到了突破。1用一张长8cm、宽5 cm的长方形纸围成一个圆柱体,这个圆柱体的侧面积是( )cm2。基础练习 设计意图:这一环节是内化知识、训练思维、培养能力、形成技能的重要环节。我准备了6道题,共分为三个层次。2.现有三个圆柱,每个圆柱都有两个不同的条件, 求侧面积(只列算式,不计算):
①C=9.42厘米,h=5厘米。
②d=8米,h=3米。
③r=2分米,h=6分米(1)侧面积:(2)底面积:(3)表面积:2×3.14×2×4=50.24 (cm2)3.14×22=12.56 (cm2)50.24+12.56×2 =75.36(cm2)3.计算下面圆柱的表面积设计意图:基础练习,重在巩固新知识,加深对新知识的理解。1.猜一猜:联系生活实际,说说生活中的这些物品与哪些面的面积有关?
(1)圆形水池的占地面积;
(2)做一个无盖水桶所需铁皮的面积;
(3)做一个油桶所需铁皮的面积;
(4)求易拉罐上商标纸的面积;
(5)在水池的内壁和底面抹水泥,求抹水泥部分的面积
(6)往大厅的柱子上涂漆,求涂漆部分的面积; 综合练习2.一个圆柱,底面周长是23厘米,高是6厘米.求它的侧面积. 3.一顶圆柱形厨师帽,高28厘米,帽顶直径20厘米,做这样一顶帽子需要用多少面料(得数保留整十平方厘米)?
注意:这道题使用的材料要比计算得到的结果多一些。因此,这里不能用四舍五入法取近似值。而要用进一法取近似值。综合练习,从学生的最近区出发,选取生活中熟悉的物体,提高学生解决实际问题的能力,增强学生学好数学的信心,做到学以致用。挑战自我如果一段底面直径20厘米的圆柱形木头,截成两截,它的表面积会有什么变化呢?增加多少?设计意图:这道题是留给稍有余力的学生做的思考题。三个层次的习题安排,既可以让学差生够得着,又可以让学优生吃得饱,一堂课下来争取做到每个学生都有所发展。 谈一谈自己有什么收获吧?设计意图:借助此环节,可以反馈这堂课的教学效果,并加深学生对知识的理解。圆柱的表面积 = 侧面积 + 2×底面面积
S = ch + 2πr22πrπd设计意图:我的板书设计很简洁,这样既突出了重点,又给学生留下了深刻的印象。 我的说课内容到此为止,谢谢各位评委和老师!
