山东省曲阜市2016-2017学年八年级下学期期末考试数学试题(WORD版含答案)
文档属性
| 名称 | 山东省曲阜市2016-2017学年八年级下学期期末考试数学试题(WORD版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-08 16:20:50 | ||
图片预览

文档简介
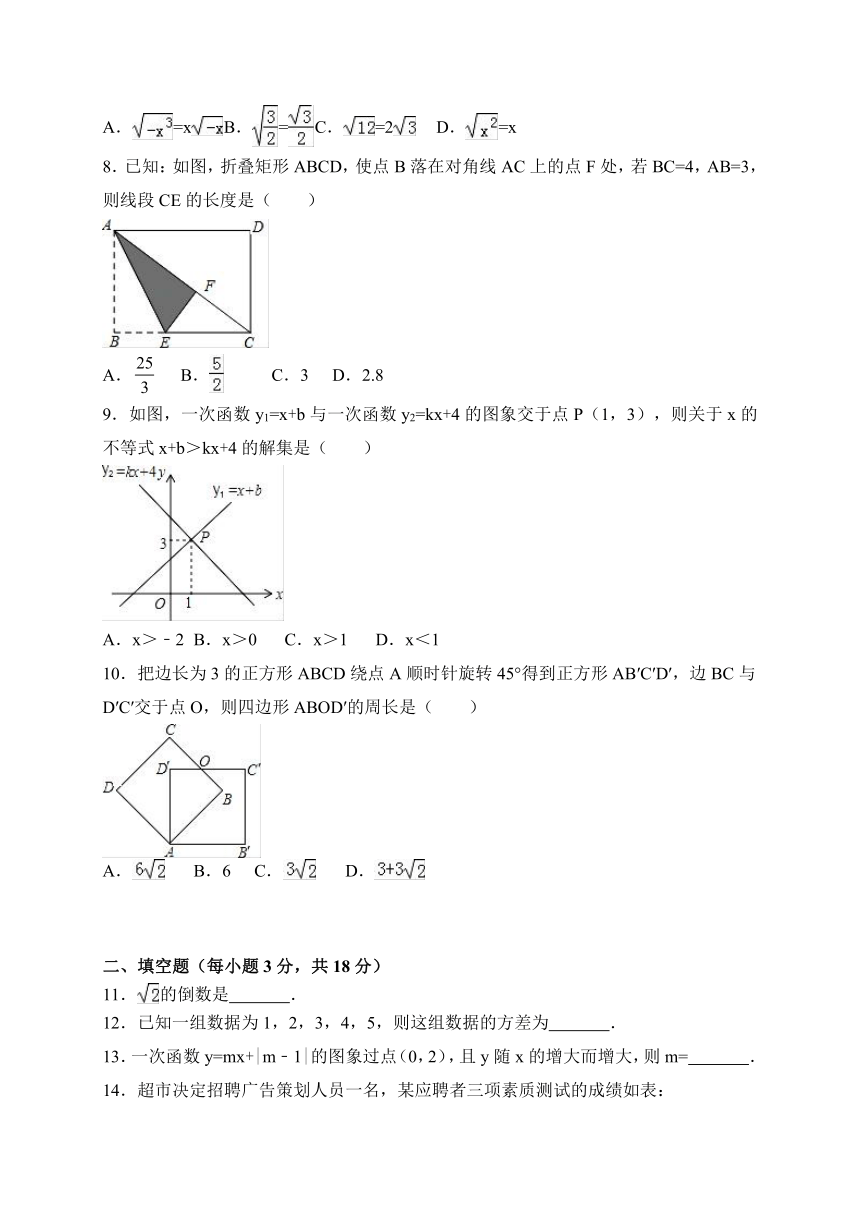
2016-2017学年山东省济宁市曲阜市八年级(下)期末考试
数学试卷
一、选择题(下列各题的四个选项中,只有一项符合题意,每小题3分,共30分)
1.下列各式中,属于最简二次根式的是( )
A.
B.
C.
D.
2.在函数y=中,自变量x的取值范围是( )
A.x>3
B.x≥3
C.x≠3
D.x≤3
3.如图, ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.10
B.14
C.20
D.22
4.如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
A.5
B.6
C.8
D.10
5.某村引进甲乙两种水稻良种,各选6块条件相同的实验田,同时播种并核定亩产,结果甲、乙两种水稻的平均产量均为550kg/亩,方差分别为S甲2=141.7,S乙2=433.3,则产量稳定,适合推广的品种为( )
A.甲、乙均可
B.甲
C.乙
D.无法确定
6.下列各曲线中表示y是x的函数的是( )
A.
B.
C.
D.
7.下列计算正确的是( )
A.=x
B.=
C.=2
D.=x
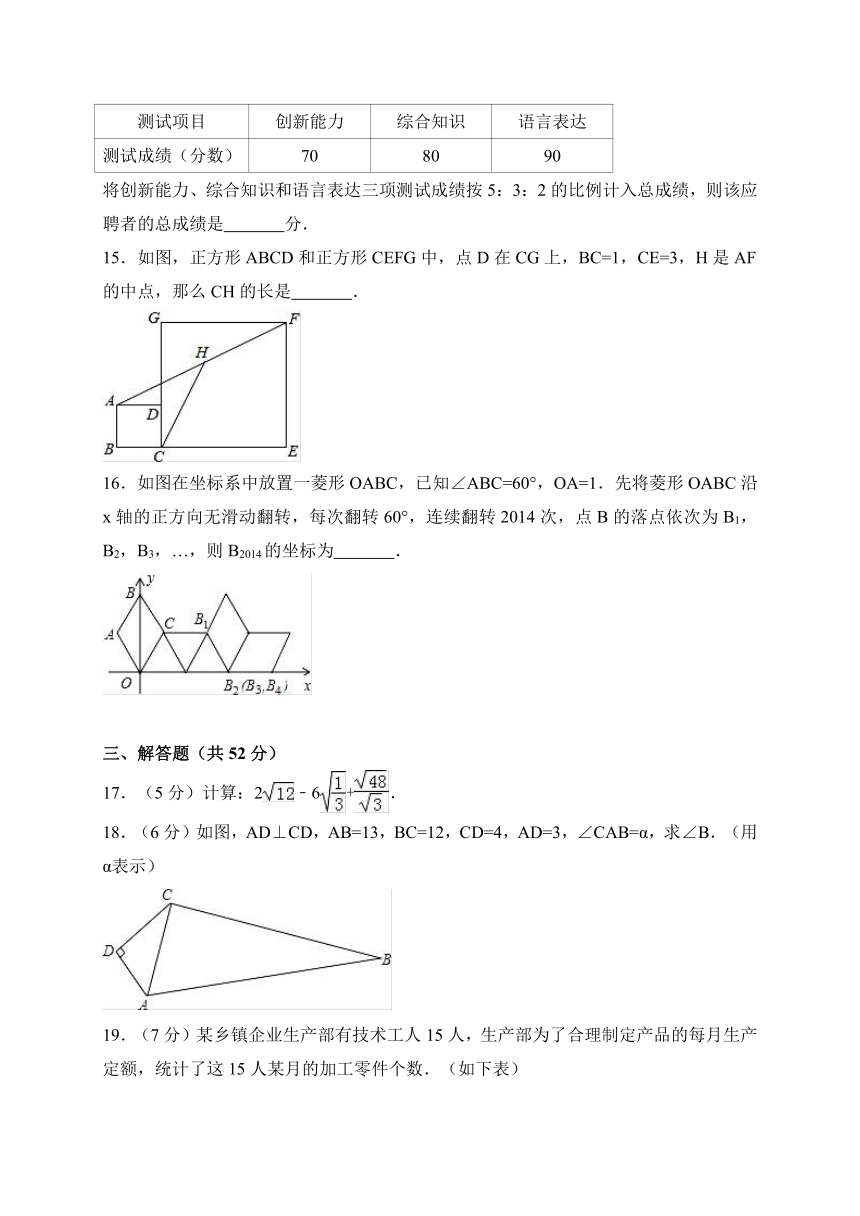
8.已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=4,AB=3,则线段CE的长度是( )
A.
B.
C.3
D.2.8
9.如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )
A.x>﹣2
B.x>0
C.x>1
D.x<1
10.把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( )
A.
B.6
C.
D.
二、填空题(每小题3分,共18分)
11.的倒数是
.
12.已知一组数据为1,2,3,4,5,则这组数据的方差为
.
13.一次函数y=mx+|m﹣1|的图象过点(0,2),且y随x的增大而增大,则m=
.
14.超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如表:
测试项目
创新能力
综合知识
语言表达
测试成绩(分数)
70
80
90
将创新能力、综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩是
分.
15.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是
.
16.如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2014次,点B的落点依次为B1,B2,B3,…,则B2014的坐标为
.
三、解答题(共52分)
17.(5分)计算:2﹣6+.
18.(6分)如图,AD⊥CD,AB=13,BC=12,CD=4,AD=3,∠CAB=α,求∠B.(用α表示)
19.(7分)某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数.(如下表)
每人加工零件数
54
45
30
24
21
12
人
数
1
1
2
6
3
2
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理?为什么?如果不合理,请你设计一个较为合理的生产定额,并说明理由.
20.(7分)如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.
(1)在图1中画出一个45°角,使点A或点B是这个角的顶点,且AB为这个角的一边;
(2)在图2中画出线段AB的垂直平分线.
21.(8分)某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种与某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象.根据图象提供的信息,解答下列问题:
(1)求yB关于x的函数解析式;
(2)如果A、B两种机器人连续搬运5个小时,那么B种机器人多搬运了多少千克?
22.(9分)如图,在矩形纸片ABCD中,AD=5,AB=3,点E为BC上一点,沿着AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D.
(1)当点E与点B的距离是多少时,四边形AEE'D是菱形?并说明理由;
(2)在(1)的条件下,求菱形AEE'D的两条对角线的长.
23.(10分)如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.
(1)当t为何值时,四边形ABDE是矩形;
(2)当t为何值时,四边形OEDC是平行四边形?
(3)连接AD,记△ADE的面积为S,求S与t的函数关系式.
数学试卷
一、选择题(下列各题的四个选项中,只有一项符合题意,每小题3分,共30分)
1.下列各式中,属于最简二次根式的是( )
A.
B.
C.
D.
2.在函数y=中,自变量x的取值范围是( )
A.x>3
B.x≥3
C.x≠3
D.x≤3
3.如图, ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.10
B.14
C.20
D.22
4.如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
A.5
B.6
C.8
D.10
5.某村引进甲乙两种水稻良种,各选6块条件相同的实验田,同时播种并核定亩产,结果甲、乙两种水稻的平均产量均为550kg/亩,方差分别为S甲2=141.7,S乙2=433.3,则产量稳定,适合推广的品种为( )
A.甲、乙均可
B.甲
C.乙
D.无法确定
6.下列各曲线中表示y是x的函数的是( )
A.
B.
C.
D.
7.下列计算正确的是( )
A.=x
B.=
C.=2
D.=x
8.已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=4,AB=3,则线段CE的长度是( )
A.
B.
C.3
D.2.8
9.如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )
A.x>﹣2
B.x>0
C.x>1
D.x<1
10.把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( )
A.
B.6
C.
D.
二、填空题(每小题3分,共18分)
11.的倒数是
.
12.已知一组数据为1,2,3,4,5,则这组数据的方差为
.
13.一次函数y=mx+|m﹣1|的图象过点(0,2),且y随x的增大而增大,则m=
.
14.超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如表:
测试项目
创新能力
综合知识
语言表达
测试成绩(分数)
70
80
90
将创新能力、综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩是
分.
15.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是
.
16.如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2014次,点B的落点依次为B1,B2,B3,…,则B2014的坐标为
.
三、解答题(共52分)
17.(5分)计算:2﹣6+.
18.(6分)如图,AD⊥CD,AB=13,BC=12,CD=4,AD=3,∠CAB=α,求∠B.(用α表示)
19.(7分)某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数.(如下表)
每人加工零件数
54
45
30
24
21
12
人
数
1
1
2
6
3
2
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理?为什么?如果不合理,请你设计一个较为合理的生产定额,并说明理由.
20.(7分)如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.
(1)在图1中画出一个45°角,使点A或点B是这个角的顶点,且AB为这个角的一边;
(2)在图2中画出线段AB的垂直平分线.
21.(8分)某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种与某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象.根据图象提供的信息,解答下列问题:
(1)求yB关于x的函数解析式;
(2)如果A、B两种机器人连续搬运5个小时,那么B种机器人多搬运了多少千克?
22.(9分)如图,在矩形纸片ABCD中,AD=5,AB=3,点E为BC上一点,沿着AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D.
(1)当点E与点B的距离是多少时,四边形AEE'D是菱形?并说明理由;
(2)在(1)的条件下,求菱形AEE'D的两条对角线的长.
23.(10分)如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.
(1)当t为何值时,四边形ABDE是矩形;
(2)当t为何值时,四边形OEDC是平行四边形?
(3)连接AD,记△ADE的面积为S,求S与t的函数关系式.
同课章节目录
