2014年全国高中数学 青年教师展评课 变量间的相关关系课件(广东深圳第二高级中学)
文档属性
| 名称 | 2014年全国高中数学 青年教师展评课 变量间的相关关系课件(广东深圳第二高级中学) |

|
|
| 格式 | zip | ||
| 文件大小 | 405.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-05 00:00:00 | ||
图片预览






文档简介
课件17张PPT。变量间的相关关系
第七届高中青年数学教师优秀课展示与研讨活动【数学实验】[实验]请在图形计算器中输入你的身高、体重数据,然后根据汇总后的数据绘制散点图。【问题引入】观察散点图,思考下列问题:
(1)从整体上看,随着身体增高,体重如何变化?(3)如果要用一个函数模型来近似地描述这两个变量之间的相关关系,你会选择哪个常见的函数类型?(2)能否根据样本数据推断某一特定身高(比如175cm)的人的大致体重? 能不能从中估计身高每增加一定高度(比如10cm),体重大约增加多少kg?若要在l1和l2中选择一条直线作为变量x,y之间线性关系的代表,你会选择谁?[实验]请根据自己的直觉,在散点图中作一条直线,让这条直线在整体上最接近样本点,并求出该直线方程。【数学实验】所有这些直线中,到底哪一条才是最接近样本点的?[问题1]从散点图看,你所作的直线是否经过每个样本点?
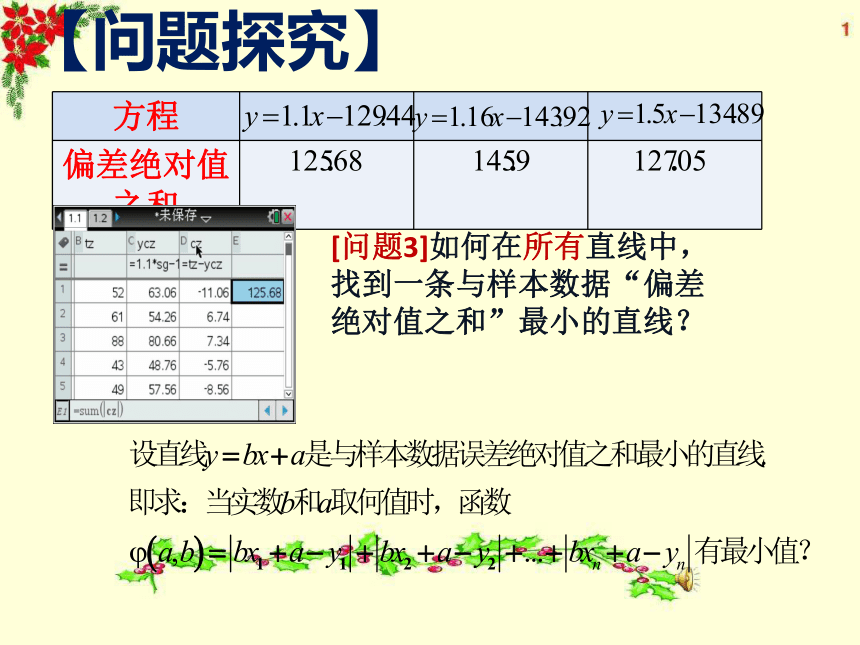
反映到代数计算上,由直线方程所计算的值与实际值是否存在差异?【问题探究】[问题2]可否将各点偏差直接相加,然后通过比较和值的大小来判定
哪个方程为“最佳”方程?[问题3]如何在所有直线中,找到一条与样本数据“偏差绝对值之和”最小的直线?【问题探究】[问题4]根据这段阅读材料,请思考回答下列问题:
(1)能不能用“偏差绝对值之和最小”为标准来确定回归直线?
(2)以“偏差绝对值之和最小”为标准来确定回归方程难点在哪里?
(3)要确定线性回归方程,“最小一乘法”是不是唯一的方法?
你能否想到其他的判定标准?【问题探究】[问题5]要从甲乙两名跳远运动员中选拔一名去参加运动会,选拔标准是:先看他们的平均成绩,如果两人的平均成绩相差无几,就再看他们成绩的稳定程度。为此对两人进行了5次比赛,得到如下数据(单位:cm),
此时应该如何做出选人的决定?
【知识回顾】[问题6]如何在所有直线中,找到一条与样本数据“偏差的平方和”最小的直线?【问题探究】【问题探究】【知识小结】【问题探究】【课堂练习】高原旅行,由于大气压低,空气含氧量少,容易产生高原反应。某同学打算去西藏那曲县旅行,但他在网上查询不到当地的大气压值,只知道那曲的海拔约为4500m . 由于大气压与海拔之间存在密切关系,为研究那曲的大气压,该同学搜集到了如下一组关于海拔和大气压的数据:试用图形计算器完成下列操作:
(1)绘制样本数据的散点图;
(2)计算海拔与大气压之间的回归方程;
(3)用此方程预测那曲(海拔高度4500m)的大气压值. 【认知升华】[问题8]那曲的大气压值一定是50.8Kpa吗?为什么?【认知升华】[问题10]两个回归方程中,哪个方程的预测值会更接近实际值?为什么?[问题9]同样是研究海拔与大气压之间的关系,为什么采集的样本数据不一样,回归方程会有所不同?另一名同学也是研究大气压与海拔的关系,他选取如下七对数据,计算得到的回归方程为 ,以此方程进行
预测,那曲的大气压值为57.85Kpa.【课堂总结】一、基本概念:
线性相关关系、回归直线、回归方程二、最小二乘法与线性回归方程三、应用回归方程进行预测
1、随机思想
2、样本估计总体的思想【分层作业】必做作业: P94—习题2.3A组T3、T4
第七届高中青年数学教师优秀课展示与研讨活动【数学实验】[实验]请在图形计算器中输入你的身高、体重数据,然后根据汇总后的数据绘制散点图。【问题引入】观察散点图,思考下列问题:
(1)从整体上看,随着身体增高,体重如何变化?(3)如果要用一个函数模型来近似地描述这两个变量之间的相关关系,你会选择哪个常见的函数类型?(2)能否根据样本数据推断某一特定身高(比如175cm)的人的大致体重? 能不能从中估计身高每增加一定高度(比如10cm),体重大约增加多少kg?若要在l1和l2中选择一条直线作为变量x,y之间线性关系的代表,你会选择谁?[实验]请根据自己的直觉,在散点图中作一条直线,让这条直线在整体上最接近样本点,并求出该直线方程。【数学实验】所有这些直线中,到底哪一条才是最接近样本点的?[问题1]从散点图看,你所作的直线是否经过每个样本点?
反映到代数计算上,由直线方程所计算的值与实际值是否存在差异?【问题探究】[问题2]可否将各点偏差直接相加,然后通过比较和值的大小来判定
哪个方程为“最佳”方程?[问题3]如何在所有直线中,找到一条与样本数据“偏差绝对值之和”最小的直线?【问题探究】[问题4]根据这段阅读材料,请思考回答下列问题:
(1)能不能用“偏差绝对值之和最小”为标准来确定回归直线?
(2)以“偏差绝对值之和最小”为标准来确定回归方程难点在哪里?
(3)要确定线性回归方程,“最小一乘法”是不是唯一的方法?
你能否想到其他的判定标准?【问题探究】[问题5]要从甲乙两名跳远运动员中选拔一名去参加运动会,选拔标准是:先看他们的平均成绩,如果两人的平均成绩相差无几,就再看他们成绩的稳定程度。为此对两人进行了5次比赛,得到如下数据(单位:cm),
此时应该如何做出选人的决定?
【知识回顾】[问题6]如何在所有直线中,找到一条与样本数据“偏差的平方和”最小的直线?【问题探究】【问题探究】【知识小结】【问题探究】【课堂练习】高原旅行,由于大气压低,空气含氧量少,容易产生高原反应。某同学打算去西藏那曲县旅行,但他在网上查询不到当地的大气压值,只知道那曲的海拔约为4500m . 由于大气压与海拔之间存在密切关系,为研究那曲的大气压,该同学搜集到了如下一组关于海拔和大气压的数据:试用图形计算器完成下列操作:
(1)绘制样本数据的散点图;
(2)计算海拔与大气压之间的回归方程;
(3)用此方程预测那曲(海拔高度4500m)的大气压值. 【认知升华】[问题8]那曲的大气压值一定是50.8Kpa吗?为什么?【认知升华】[问题10]两个回归方程中,哪个方程的预测值会更接近实际值?为什么?[问题9]同样是研究海拔与大气压之间的关系,为什么采集的样本数据不一样,回归方程会有所不同?另一名同学也是研究大气压与海拔的关系,他选取如下七对数据,计算得到的回归方程为 ,以此方程进行
预测,那曲的大气压值为57.85Kpa.【课堂总结】一、基本概念:
线性相关关系、回归直线、回归方程二、最小二乘法与线性回归方程三、应用回归方程进行预测
1、随机思想
2、样本估计总体的思想【分层作业】必做作业: P94—习题2.3A组T3、T4
