广东省深圳市翠园中学2014-2015学年高二下学期数学选修2-1复习综合测试题(含答案)
文档属性
| 名称 | 广东省深圳市翠园中学2014-2015学年高二下学期数学选修2-1复习综合测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 320.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-06 00:00:00 | ||
图片预览



文档简介
2-1复习题
一、选择题答案:(本大题共10小题,每小题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
1.设命题甲:平面内有两定点和动点P,使是定值;命题乙:点P的轨迹是椭圆,则甲是乙的
(
)
A.充分但不必要条件
B.必要但不充分条件
C.充要条件
D.既不充分也不必要条
2.一动圆与圆O:x2+y2=1外切,又与圆L:x2+y2-6x+8=0内切,那么动圆圆心轨迹是
(
)
A.双曲线的一支
B.椭圆
C.抛物线
D.圆
3.过抛物线的焦点的直线交抛物线于A、B两点,O为坐标原点,则的值是
(
)
A.3
B.-3
C.12
D.-12
4.椭圆=1(a>b>0)上两点A、B与中心O的连线互相垂直,则的值为
(
)
A.
B.
C.
D.
5.椭圆的离心率e=,以右焦点为中心将椭圆逆时针旋转后所得到椭圆的一条准线为y=,则原椭圆的方程为
(
)
A+=1
B+=1
C+=1
D+=1
6.若动圆的圆心在抛物线=12y上,
且直线y+3=0相切,则此动圆恒过定点
(
)
A.
(0,2)
B.(0,
3)
C.(0,3)
D.(0,6)
7.如图,∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2cm,那么PC与平面ABC所成角的大小为(
)。
A.30°
B.45°
C.60°
D.75°
8.设F1、F2分别为双曲线(a>0,b>0)的左、右焦点,P为双曲线右支上任一点。若的最小值为8a,则该双贡线离心率e的取值范围是.
A.(0,2)
B.(1,3)
C.[2,3]
D.[3,+∞]
9、如图,已知抛物线的焦点恰好是椭圆的右焦点,且两条曲线的连线过,则该椭圆的离心率为
(A)
(B)
(C)
(D)
10.设O点是△ABC的外心,点P满足,则点P一定是△ABC的(
)
A.重心
B.垂心
C.内心
D.外心
二.填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)
11.已知向量、的夹角为,||=2,||=1,且⊥,那么实数=
.
12.已知圆x2+y2-6x-7=0与抛物线y2=2px(p>0)的准线相切,则p=___________________..
13.在二面角的棱a上有一点A,在面内引射线AB且AB与a成45°角,AB与平面成30°的角,则二面角为_______________.
14.已知、为双曲线的焦点,M为双曲线上一点,MF1垂直于轴,且,则该双曲线的离心率为
________.
三、解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤)
15.
(本小题满分12分)如图,OA是双曲线的实半轴,OB是虚半轴,F为焦点,且∠BAO=30°,S△ABF=,求该双曲线的方程.
16.
(本小题满分12分设点O、A、B、C为同一平面内四点,且,,
判断的形状.
17.(本小题满分12分)
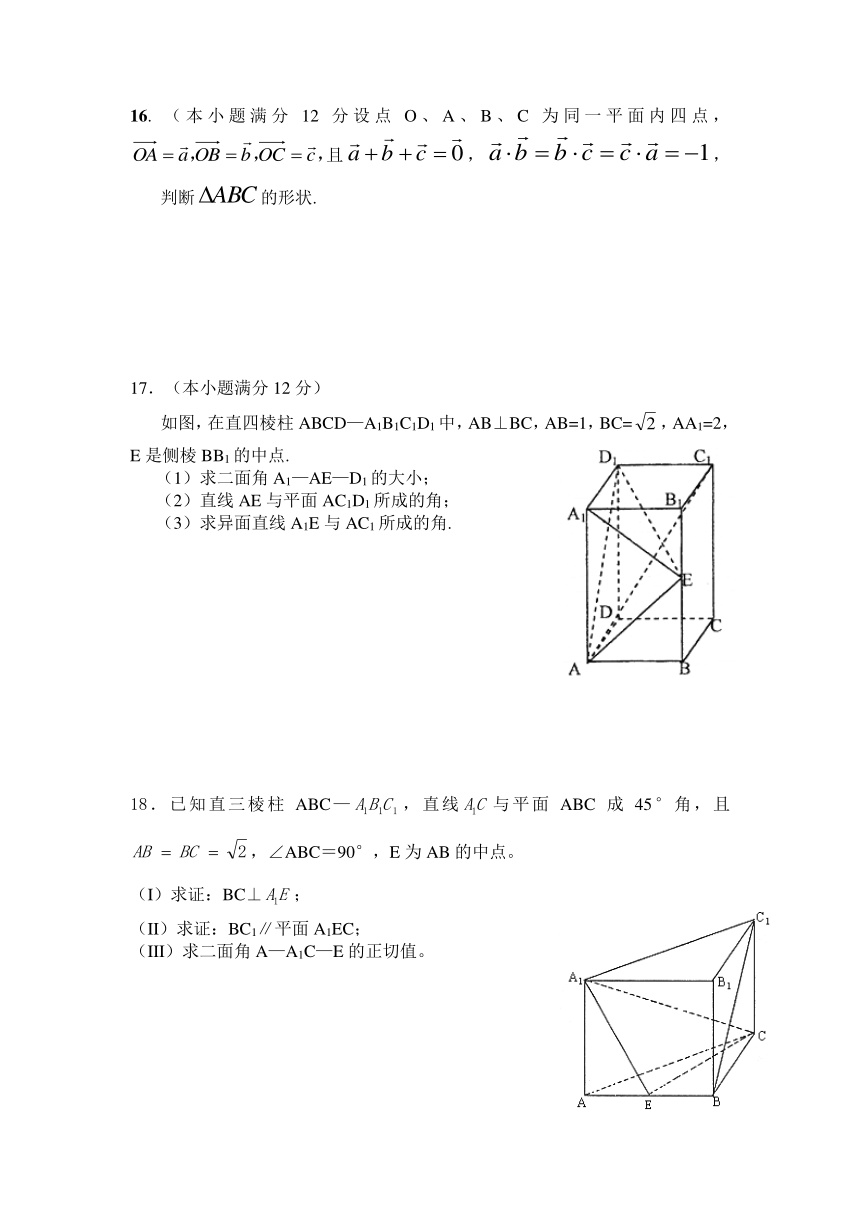
如图,在直四棱柱ABCD—A1B1C1D1中,AB⊥BC,AB=1,BC=,AA1=2,E是侧棱BB1的中点.
(1)求二面角A1—AE—D1的大小;
(2)直线AE与平面AC1D1所成的角;
(3)求异面直线A1E与AC1所成的角.
18.已知直三棱柱ABC—,直线与平面ABC成45°角,且,∠ABC=90°,E为AB的中点。
(I)求证:BC⊥;
(II)求证:BC1∥平面A1EC;
(III)求二面角A—A1C—E的正切值。
19.(本小题满分12分)
已知向量且.
(1)求点Q的轨迹C的方程;
(2)设曲线C与直线相交于不同的两点M、N,又点A(0,-1),当
时,求实数的取值范围.
20.(本小题满分12分)已知双曲线=1(a>0,b>0)的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.
(1)求证:PF⊥l;
(2)若|PF|=3,且双曲线的离心率e=,求该双曲线方程;
(3)延长FP交双曲线左准线l1和左支分别为点M、N,若M为PN的中点,求双曲线的离心率.
2-1复习题答案
一、选择题答案:(本大题共10小题,每小题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
B
D
A
C
B
B
A
B
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)
11.已知向量、的夹角为,||=2,||=1,且⊥,那么实数=
.
12.已知圆x2+y2-6x-7=0与抛物线y2=2px(p>0)的准线相切,则p=___2
___.
13.在二面角的棱a上有一点A,在面内引射线AB且AB与a成45°角,AB与平面成30°的角,则二面角为_______________
14.已知、为双曲线的焦点,M为双曲线上一点,MF1垂直于轴,且,则该双曲线的离心率为
___
三、解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤)
15.如图,OA是双曲线的实半轴,OB是虚半轴,F为焦点,且∠BAO=30°,S△ABF=,求该双曲线的方程.
16.设点O、A、B、C为同一平面内四点,且,,
判断的形状.
解:
.同理,
又,同理
,为等边三角形.
17.(本小题满分12分)
如图,在直四棱柱ABCD—A1B1C1D1中,AB⊥BC,AB=1,BC=,AA1=2,E是侧棱BB1的中点.
(1)求二面角A1—AE—D1的大小;
(2)直线AE与平面AC1D1所成的角;
(3)求异面直线A1E与AC1所成的角.
17.解:(1)⊥面ABB1A1,∴D1A1⊥AE.
又∵AE=A1E=
∴AE⊥面A1ED1,∴D1E⊥AE,∴∠A1ED1即为二面角A1—AE—D1的平面角.
在Rt△A1ED1中,∠D1A1E=,A1D=A1E,故二面角A1—AE—D1的平面角为……4分
(2)由已知得面ABC1D2⊥面BC1,过E和EF⊥BC于F,连接AF,则EF⊥面ABC1D1,
∴∠EAF即为直线AE与平面ABC1D1所成的角.
在R
t△AEF中,∠AFE=,AE=,EF=,
直线AE与平面ABC1D1所成的角为………………8分
(3)延长B1B到M使BM=BE,连AM,则AM//A1E
∴∠MAC1即为异面直线A1E与AC1所成的角或其补角.
在
△AMC1中,AC1=,AM=,MC1=
直线A1E与AC1所成的角为………………12分
18.已知直三棱柱ABC—,直线与平面ABC成45°角,且,∠ABC=90°,E为AB的中点。
(I)求证:BC⊥;
(II)求证:BC1∥平面A1EC;
(III)求二面角A—A1C—E的正切值。
18.本小题满分12分)
解:(I)在直三棱柱ABC—中,AA1⊥面ABC
∴AA1⊥BC
又∵∠ABC=90°
∴BC⊥面ABB1A1
又面ABB1A1
∴BC⊥A1E
3分
(II)连接AC1交A1C于点F,则F为AC1的中点
又∵E为AB的中点
∴EF∥BC1
5分
又EF面A1CE
∴BC1∥面A1CE
6分
(III)∵面ACA1⊥面ABC,作EO⊥AC,则EO⊥面ACA1,
作OG⊥A1C,则∠OGE为二面角A—A1C—E的平面角
8分
又∵直线A1C与面ABC成45°角
∴∠A1CA=45°
又,E为AB的中点
∴
∴
11分
∴
∴二面角A—A1C—E的正切值为
12分
19.(本小题满分12分)
已知向量且.
(1)求点Q的轨迹C的方程;
(2)设曲线C与直线相交于不同的两点M、N,又点A(0,-1),当
时,求实数的取值范围.
19.解:(Ⅰ)
得
点的轨迹C的方程为……………………6分
(Ⅱ)由得
由于直线与椭圆有两个交点,
①
(1)当,设P为弦MN的中点,
从而
又|AM|=|AN|,
则
即
②
把②代入①得,解得;由②得,解得,
故所求m的取值范围是(……………………10分
(2)当时,|AM|=|AN|,
故所求m的取值范围是(-1,1).
当时,m的取值范围是,当时,m的取值范围是(-1,1).……12分
20.(本小题满分12分)已知双曲线=1(a>0,b>0)的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.
(1)求证:PF⊥l;
(2)若|PF|=3,且双曲线的离心率e=,求该双曲线方程;
(3)延长FP交双曲线左准线l1和左支分别为点M、N,若M为PN的中点,求双曲线的离心率.
20.(1)右准线为x=,由对称性不妨设渐近线l为y=x,
则P(),又F(c,0),∴,
2分
又∵,∴kPF·kl=-=-1,
∴PF⊥l.
4分
(2)∵|PF|的长即F(c,0)到l:bx-ay=0的距离,
∴=3,即b=3,
6分
又,∴,∴a=4,
故双曲线方程为=1.
8分
(3)PF的方程为:y=-(x-c),
由得,
9分
∵M是PN的中点
∴,
10分
∵N在双曲线上,
∴,
即,
令t=e2,则t2-10t+25=0,∴t=5,即e=.
12分
一、选择题答案:(本大题共10小题,每小题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
1.设命题甲:平面内有两定点和动点P,使是定值;命题乙:点P的轨迹是椭圆,则甲是乙的
(
)
A.充分但不必要条件
B.必要但不充分条件
C.充要条件
D.既不充分也不必要条
2.一动圆与圆O:x2+y2=1外切,又与圆L:x2+y2-6x+8=0内切,那么动圆圆心轨迹是
(
)
A.双曲线的一支
B.椭圆
C.抛物线
D.圆
3.过抛物线的焦点的直线交抛物线于A、B两点,O为坐标原点,则的值是
(
)
A.3
B.-3
C.12
D.-12
4.椭圆=1(a>b>0)上两点A、B与中心O的连线互相垂直,则的值为
(
)
A.
B.
C.
D.
5.椭圆的离心率e=,以右焦点为中心将椭圆逆时针旋转后所得到椭圆的一条准线为y=,则原椭圆的方程为
(
)
A+=1
B+=1
C+=1
D+=1
6.若动圆的圆心在抛物线=12y上,
且直线y+3=0相切,则此动圆恒过定点
(
)
A.
(0,2)
B.(0,
3)
C.(0,3)
D.(0,6)
7.如图,∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2cm,那么PC与平面ABC所成角的大小为(
)。
A.30°
B.45°
C.60°
D.75°
8.设F1、F2分别为双曲线(a>0,b>0)的左、右焦点,P为双曲线右支上任一点。若的最小值为8a,则该双贡线离心率e的取值范围是.
A.(0,2)
B.(1,3)
C.[2,3]
D.[3,+∞]
9、如图,已知抛物线的焦点恰好是椭圆的右焦点,且两条曲线的连线过,则该椭圆的离心率为
(A)
(B)
(C)
(D)
10.设O点是△ABC的外心,点P满足,则点P一定是△ABC的(
)
A.重心
B.垂心
C.内心
D.外心
二.填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)
11.已知向量、的夹角为,||=2,||=1,且⊥,那么实数=
.
12.已知圆x2+y2-6x-7=0与抛物线y2=2px(p>0)的准线相切,则p=___________________..
13.在二面角的棱a上有一点A,在面内引射线AB且AB与a成45°角,AB与平面成30°的角,则二面角为_______________.
14.已知、为双曲线的焦点,M为双曲线上一点,MF1垂直于轴,且,则该双曲线的离心率为
________.
三、解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤)
15.
(本小题满分12分)如图,OA是双曲线的实半轴,OB是虚半轴,F为焦点,且∠BAO=30°,S△ABF=,求该双曲线的方程.
16.
(本小题满分12分设点O、A、B、C为同一平面内四点,且,,
判断的形状.
17.(本小题满分12分)
如图,在直四棱柱ABCD—A1B1C1D1中,AB⊥BC,AB=1,BC=,AA1=2,E是侧棱BB1的中点.
(1)求二面角A1—AE—D1的大小;
(2)直线AE与平面AC1D1所成的角;
(3)求异面直线A1E与AC1所成的角.
18.已知直三棱柱ABC—,直线与平面ABC成45°角,且,∠ABC=90°,E为AB的中点。
(I)求证:BC⊥;
(II)求证:BC1∥平面A1EC;
(III)求二面角A—A1C—E的正切值。
19.(本小题满分12分)
已知向量且.
(1)求点Q的轨迹C的方程;
(2)设曲线C与直线相交于不同的两点M、N,又点A(0,-1),当
时,求实数的取值范围.
20.(本小题满分12分)已知双曲线=1(a>0,b>0)的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.
(1)求证:PF⊥l;
(2)若|PF|=3,且双曲线的离心率e=,求该双曲线方程;
(3)延长FP交双曲线左准线l1和左支分别为点M、N,若M为PN的中点,求双曲线的离心率.
2-1复习题答案
一、选择题答案:(本大题共10小题,每小题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
B
D
A
C
B
B
A
B
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)
11.已知向量、的夹角为,||=2,||=1,且⊥,那么实数=
.
12.已知圆x2+y2-6x-7=0与抛物线y2=2px(p>0)的准线相切,则p=___2
___.
13.在二面角的棱a上有一点A,在面内引射线AB且AB与a成45°角,AB与平面成30°的角,则二面角为_______________
14.已知、为双曲线的焦点,M为双曲线上一点,MF1垂直于轴,且,则该双曲线的离心率为
___
三、解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤)
15.如图,OA是双曲线的实半轴,OB是虚半轴,F为焦点,且∠BAO=30°,S△ABF=,求该双曲线的方程.
16.设点O、A、B、C为同一平面内四点,且,,
判断的形状.
解:
.同理,
又,同理
,为等边三角形.
17.(本小题满分12分)
如图,在直四棱柱ABCD—A1B1C1D1中,AB⊥BC,AB=1,BC=,AA1=2,E是侧棱BB1的中点.
(1)求二面角A1—AE—D1的大小;
(2)直线AE与平面AC1D1所成的角;
(3)求异面直线A1E与AC1所成的角.
17.解:(1)⊥面ABB1A1,∴D1A1⊥AE.
又∵AE=A1E=
∴AE⊥面A1ED1,∴D1E⊥AE,∴∠A1ED1即为二面角A1—AE—D1的平面角.
在Rt△A1ED1中,∠D1A1E=,A1D=A1E,故二面角A1—AE—D1的平面角为……4分
(2)由已知得面ABC1D2⊥面BC1,过E和EF⊥BC于F,连接AF,则EF⊥面ABC1D1,
∴∠EAF即为直线AE与平面ABC1D1所成的角.
在R
t△AEF中,∠AFE=,AE=,EF=,
直线AE与平面ABC1D1所成的角为………………8分
(3)延长B1B到M使BM=BE,连AM,则AM//A1E
∴∠MAC1即为异面直线A1E与AC1所成的角或其补角.
在
△AMC1中,AC1=,AM=,MC1=
直线A1E与AC1所成的角为………………12分
18.已知直三棱柱ABC—,直线与平面ABC成45°角,且,∠ABC=90°,E为AB的中点。
(I)求证:BC⊥;
(II)求证:BC1∥平面A1EC;
(III)求二面角A—A1C—E的正切值。
18.本小题满分12分)
解:(I)在直三棱柱ABC—中,AA1⊥面ABC
∴AA1⊥BC
又∵∠ABC=90°
∴BC⊥面ABB1A1
又面ABB1A1
∴BC⊥A1E
3分
(II)连接AC1交A1C于点F,则F为AC1的中点
又∵E为AB的中点
∴EF∥BC1
5分
又EF面A1CE
∴BC1∥面A1CE
6分
(III)∵面ACA1⊥面ABC,作EO⊥AC,则EO⊥面ACA1,
作OG⊥A1C,则∠OGE为二面角A—A1C—E的平面角
8分
又∵直线A1C与面ABC成45°角
∴∠A1CA=45°
又,E为AB的中点
∴
∴
11分
∴
∴二面角A—A1C—E的正切值为
12分
19.(本小题满分12分)
已知向量且.
(1)求点Q的轨迹C的方程;
(2)设曲线C与直线相交于不同的两点M、N,又点A(0,-1),当
时,求实数的取值范围.
19.解:(Ⅰ)
得
点的轨迹C的方程为……………………6分
(Ⅱ)由得
由于直线与椭圆有两个交点,
①
(1)当,设P为弦MN的中点,
从而
又|AM|=|AN|,
则
即
②
把②代入①得,解得;由②得,解得,
故所求m的取值范围是(……………………10分
(2)当时,|AM|=|AN|,
故所求m的取值范围是(-1,1).
当时,m的取值范围是,当时,m的取值范围是(-1,1).……12分
20.(本小题满分12分)已知双曲线=1(a>0,b>0)的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.
(1)求证:PF⊥l;
(2)若|PF|=3,且双曲线的离心率e=,求该双曲线方程;
(3)延长FP交双曲线左准线l1和左支分别为点M、N,若M为PN的中点,求双曲线的离心率.
20.(1)右准线为x=,由对称性不妨设渐近线l为y=x,
则P(),又F(c,0),∴,
2分
又∵,∴kPF·kl=-=-1,
∴PF⊥l.
4分
(2)∵|PF|的长即F(c,0)到l:bx-ay=0的距离,
∴=3,即b=3,
6分
又,∴,∴a=4,
故双曲线方程为=1.
8分
(3)PF的方程为:y=-(x-c),
由得,
9分
∵M是PN的中点
∴,
10分
∵N在双曲线上,
∴,
即,
令t=e2,则t2-10t+25=0,∴t=5,即e=.
12分
