广东省深圳市沙井中学高中数学 3.3.2函数的极值与导数课件 苏教版选修1-1
文档属性
| 名称 | 广东省深圳市沙井中学高中数学 3.3.2函数的极值与导数课件 苏教版选修1-1 |

|
|
| 格式 | zip | ||
| 文件大小 | 201.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-03 00:00:00 | ||
图片预览






文档简介
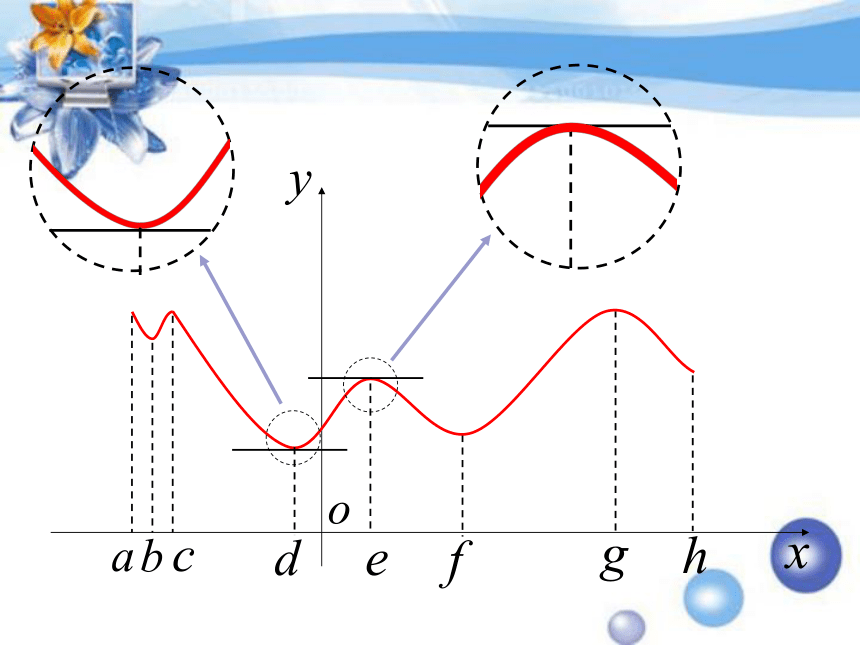
课件15张PPT。3.3.2 函数的极值与导数第三章 导数及其应用我们把点d叫做函数y=f(x)的极小值点,
f(d)叫做函数y=f(x)的极小值。我们把点e叫做函数y=f(x)的极大值点,
f(e)叫做函数y=f(x)的极大值。极小值点、极大值点统称为极值点极小值、极大值统称为极值极大值一定大于极小值吗?不一定一、应用知识
例1:求f(x)=x2-x-2的极值.二、知识巩固
例2、求函数f(x)=x3-12x+12的极值。 得x=2,或x=-2 当x=-2时,f(x)有极大值f(-2)=28当x=2时,f(x)有极小值f(2)=-4图象如右三、知识拓延
例3、已知函数f(x)=ax3+bx2-2x在x=-2,x=1
处取得极值,求函数的解析式
.四、能力拔高(1)由图像可知:(2)注意:数形结合以及函数与方程思想的应用A注意:数形结合以及原函数与导函数图像的区别导数值为0的点一定是函数的极值点吗?思考但x=0不是函数的极值点导数为零的点是
该点为极值点的必要条件,
而不是充分条件.小结
f(d)叫做函数y=f(x)的极小值。我们把点e叫做函数y=f(x)的极大值点,
f(e)叫做函数y=f(x)的极大值。极小值点、极大值点统称为极值点极小值、极大值统称为极值极大值一定大于极小值吗?不一定一、应用知识
例1:求f(x)=x2-x-2的极值.二、知识巩固
例2、求函数f(x)=x3-12x+12的极值。 得x=2,或x=-2 当x=-2时,f(x)有极大值f(-2)=28当x=2时,f(x)有极小值f(2)=-4图象如右三、知识拓延
例3、已知函数f(x)=ax3+bx2-2x在x=-2,x=1
处取得极值,求函数的解析式
.四、能力拔高(1)由图像可知:(2)注意:数形结合以及函数与方程思想的应用A注意:数形结合以及原函数与导函数图像的区别导数值为0的点一定是函数的极值点吗?思考但x=0不是函数的极值点导数为零的点是
该点为极值点的必要条件,
而不是充分条件.小结
