广东省深圳市西丽第二中学北师大版数学七年级上册第三章整式及其加减章末总结课件(共10张ppt)
文档属性
| 名称 | 广东省深圳市西丽第二中学北师大版数学七年级上册第三章整式及其加减章末总结课件(共10张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 719.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-03 00:00:00 | ||
图片预览




文档简介
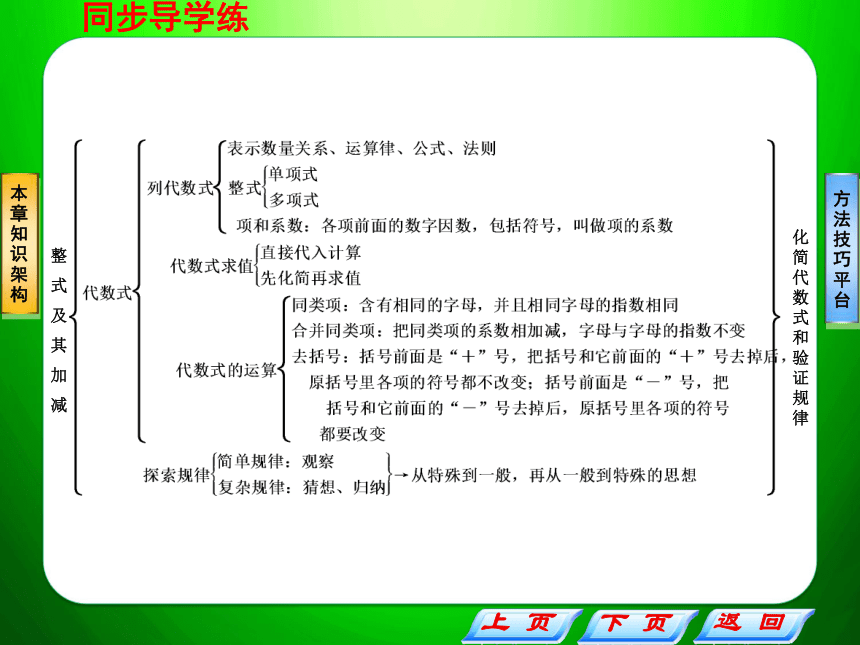
课件10张PPT。本章知识架构整式及其加减化简代数式和验证规律方法技巧平台一、整体思想
整体思想是一种重要的数学思想.整体思想是指在考虑数学问题时,不是着眼于它的局部特征,而是把注意力放在问题的整体结构上,把某些式子或图形看成一个整体进行解决问题的思想方法.在代数式的化简求值时,常采用整体代入的解题策略,使计算更简便,而有些问题也只有从整体考虑才能解决问题.
若2x+3y=2 012,试求代数式2(3x-2y)-(x-y)+(-x+9y)的值.
分析:本题不能直接求出x,y的值,也不能直接整体代入,可以先将所求代数式去括号化简后,再考虑把2x+3y=2 012整体代入.
解:2(3x-2y)-(x-y)+(-x+9y)
=6x-4y-x+y-x+9y
=4x+6y
=2(2x+3y).
当2x+3y=2 012时,原式=2×2 012=4 024.二、由特殊到一般思想
揭示事物的规律常用的方法是“由特殊到一般”,即从几个简单的、个别的具有代表性的例子入手,去分析、探索、归纳出一般的规律或性质,比如学习有理数的运算的性质推导时就用的这样的方法.
反过来,用得出的性质或一般的规律去解决特殊的问题或实际问题,这是“由一般到特殊”的数学思想的体现.如根据去括号法则去括号.
列代数式和求代数式的值以及探索规律等题目都体现了这种思想方法.
研究下列算式,你会发现什么规律:
1×3+1=4=22;
2×4+1=9=32;
3×5+1=16=42;
4×6+1=25=52;
……
(1)请你将找出的规律用字母n表示出来;
(2)根据上面的规律,写出第2 012个算式.分析:(1)对比上面4个算式,可以发现:一个正整数乘以比它大2的数再加上1等于该正整数与1的和的平方;(2)第2 012个算式即当n=2 012时的算式.
解:(1)n(n+2)+1=(n+1)2(n为正整数);
(2)当n=2 012时,算式为:
2 012×2 014+1=4 052 169=2 0132.
整体思想是一种重要的数学思想.整体思想是指在考虑数学问题时,不是着眼于它的局部特征,而是把注意力放在问题的整体结构上,把某些式子或图形看成一个整体进行解决问题的思想方法.在代数式的化简求值时,常采用整体代入的解题策略,使计算更简便,而有些问题也只有从整体考虑才能解决问题.
若2x+3y=2 012,试求代数式2(3x-2y)-(x-y)+(-x+9y)的值.
分析:本题不能直接求出x,y的值,也不能直接整体代入,可以先将所求代数式去括号化简后,再考虑把2x+3y=2 012整体代入.
解:2(3x-2y)-(x-y)+(-x+9y)
=6x-4y-x+y-x+9y
=4x+6y
=2(2x+3y).
当2x+3y=2 012时,原式=2×2 012=4 024.二、由特殊到一般思想
揭示事物的规律常用的方法是“由特殊到一般”,即从几个简单的、个别的具有代表性的例子入手,去分析、探索、归纳出一般的规律或性质,比如学习有理数的运算的性质推导时就用的这样的方法.
反过来,用得出的性质或一般的规律去解决特殊的问题或实际问题,这是“由一般到特殊”的数学思想的体现.如根据去括号法则去括号.
列代数式和求代数式的值以及探索规律等题目都体现了这种思想方法.
研究下列算式,你会发现什么规律:
1×3+1=4=22;
2×4+1=9=32;
3×5+1=16=42;
4×6+1=25=52;
……
(1)请你将找出的规律用字母n表示出来;
(2)根据上面的规律,写出第2 012个算式.分析:(1)对比上面4个算式,可以发现:一个正整数乘以比它大2的数再加上1等于该正整数与1的和的平方;(2)第2 012个算式即当n=2 012时的算式.
解:(1)n(n+2)+1=(n+1)2(n为正整数);
(2)当n=2 012时,算式为:
2 012×2 014+1=4 052 169=2 0132.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
