广东省深圳市第三高级中学高中数学必修二13空间几何体的表面积和体积教案
文档属性
| 名称 | 广东省深圳市第三高级中学高中数学必修二13空间几何体的表面积和体积教案 |  | |
| 格式 | zip | ||
| 文件大小 | 583.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-03 10:33:43 | ||
图片预览

文档简介
( http: / / www.21cnjy.com )
【教学过程】
表面积公式
多面体(棱柱、棱锥、棱台):就是__________________的面积的和。
旋转体:(1)圆柱
=________________
=
____________
____________
圆锥
=________________
=
____________
____________
圆台=
=
____________
____________
体积公式
柱体:V=
__________
椎体:V=
__________
台体:V=_________________
思考:你能发现柱体、椎体、台体三者的体积公式之间的关系吗?
例1.已知圆柱和圆锥的高、底面半径均分别相等。若圆柱的底面半径为
( http: / / www.21cnjy.com ),圆柱侧面积为S,求圆锥的侧面积。
变式训练:若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为(
)
A.
( http: / / www.21cnjy.com )B.
( http: / / www.21cnjy.com )C.
( http: / / www.21cnjy.com )
D.
( http: / / www.21cnjy.com )
例2.如果一个空间几何体的正视图与侧视图均为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的体积为(
)
A.
( http: / / www.21cnjy.com )
B.
( http: / / www.21cnjy.com )
C.
( http: / / www.21cnjy.com )
D.
( http: / / www.21cnjy.com )
变式训练:
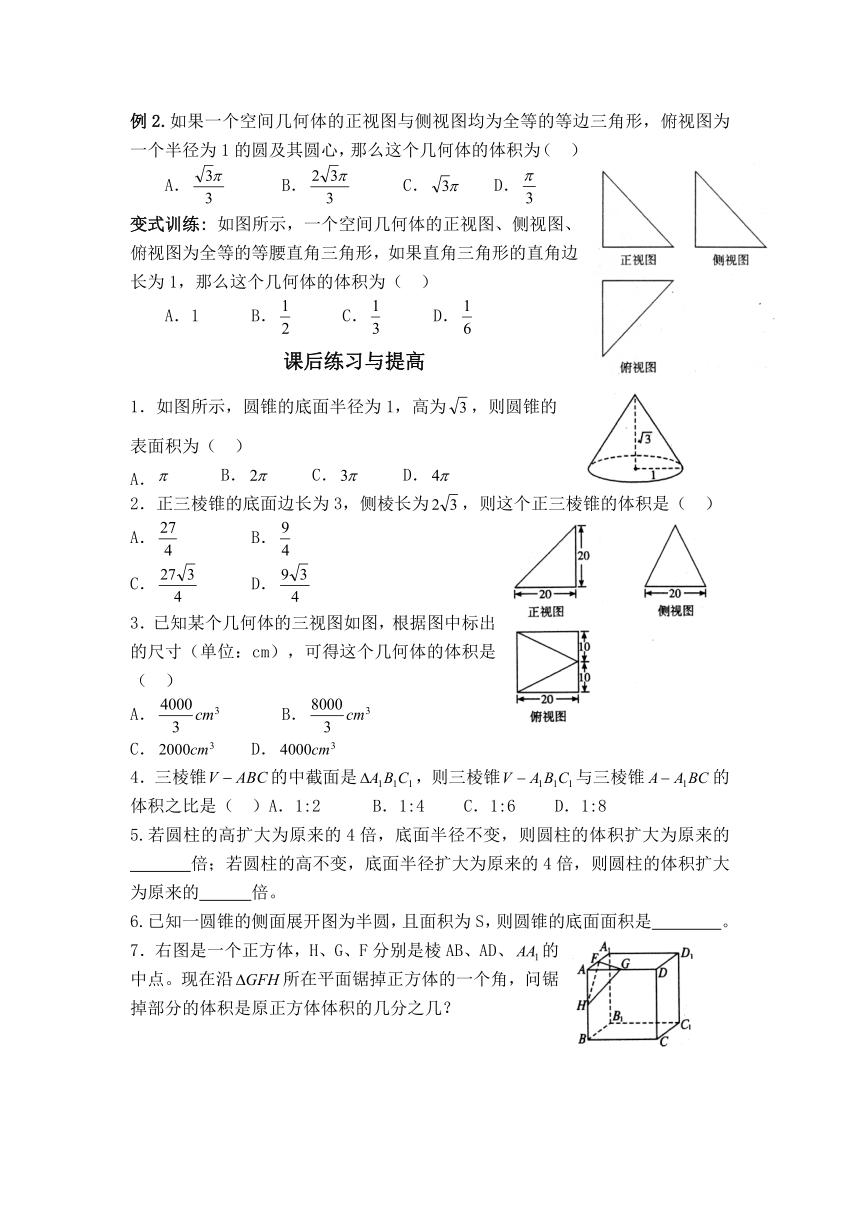
如图所示,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为(
)
A.1
B.
( http: / / www.21cnjy.com )
C.
( http: / / www.21cnjy.com )
D.
( http: / / www.21cnjy.com )
课后练习与提高
1.如图所示,圆锥的底面半径为1,高为
( http: / / www.21cnjy.com ),则圆锥的
表面积为(
)
( http: / / www.21cnjy.com )
B.
( http: / / www.21cnjy.com )
C.
( http: / / www.21cnjy.com )
D.
( http: / / www.21cnjy.com )
2.正三棱锥的底面边长为3,侧棱长为
( http: / / www.21cnjy.com ),则这个正三棱锥的体积是(
)
A.
( http: / / www.21cnjy.com )
B.
( http: / / www.21cnjy.com )
C.
( http: / / www.21cnjy.com )
D.
( http: / / www.21cnjy.com )
3.已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是(
)
A.
( http: / / www.21cnjy.com )
B.
( http: / / www.21cnjy.com )
C.
( http: / / www.21cnjy.com )
D.
( http: / / www.21cnjy.com )
4.三棱锥
( http: / / www.21cnjy.com )的中截面是
( http: / / www.21cnjy.com ),则三棱锥
( http: / / www.21cnjy.com )与三棱锥
( http: / / www.21cnjy.com )的体积之比是(
)A.1:2
B.1:4
C.1:6
D.1:8
5.若圆柱的高扩大为原来的4倍,底面半径不变,则圆柱的体积扩大为原来的
倍;若圆柱的高不变,底面半径扩大为原来的4倍,则圆柱的体积扩大为原来的
倍。
6.已知一圆锥的侧面展开图为半圆,且面积为S,则圆锥的底面面积是
。
7.右图是一个正方体,H、G、F分别是棱AB、AD、
( http: / / www.21cnjy.com )的中点。现在沿
( http: / / www.21cnjy.com )所在平面锯掉正方体的一个角,问锯掉部分的体积是原正方体体积的几分之几?
1.
3.2
球的体积和表面积
【教学目标】
(1)能运用球的面积和体积公式灵活解决实际问题。
(2)培养学生的空间思维能力和空间想象能力。
【教学重难点】
重点:球的体积和面积公式的实际应用
难点:应用体积和面积公式中空间想象能力的形成。
【教学过程】
球的大小是与球的半径有关,如何用球半径来表示球的体积和面积?
球的体积和面积公式:半径是R的球的体积V=
,表面积S=
例1.一种空心钢球的质量是732πg,外径是5cm,求它的内径.
(钢密度9g/cm3)
求空心钢球的体积
。
变式:正方体的棱长为2,顶点都在同一球面上,则球的体积为____________
例2
在球心同侧有相距9的两个平行截面,它们的面积分别为49π和400π,求球的表面积。
变式:长方体的一个顶点上三条棱长分别为3、4、5,是它的八个顶点都在同一球面上,则这个球的表面积是
。
课后练习与提高
1、将气球的半径扩大1倍,它的体积增大到原来的()倍
A2
B4
C8
D16
2.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是(
)
A.16π
B.20π
C.24π
D.32π
3.三个球的半径之比为1∶2∶3,那么最大球的表面积是其余两个球的表面积之和的(
)
A.1倍
B.2倍
C.
( http: / / www.21cnjy.com )倍
D.
( http: / / www.21cnjy.com )倍.
4.若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为____________.
5.一个球与正四面体的六条棱都相切,若正四面体的棱长为a,则这个球的体积为_____________..
6、若三个球的表面积之比是1:2:3,则它们的体积之比是_____________..
7、用与球心距离为2的平面去截球,若球的体积为36,截面圆的面积_____.
一个直径为32cm的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9cm,求此球的半径。
9、
下图是一个底面直径为20
cm的装
( http: / / www.21cnjy.com )有一部分水的圆柱形玻璃杯,水中放着一个底面直径为6
cm,高为20
cm的一个圆锥形铅锤,当铅锤从水中取出后,杯里的水将下降几厘米?
( http: / / www.21cnjy.com )
综合练习:1、已知一几何体的三视图如下图,试求其表面积与体积.
2、已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形
( http: / / www.21cnjy.com ).
(1)求该几何体的体积V;
(2)求该几何体的侧面积S
【教学过程】
表面积公式
多面体(棱柱、棱锥、棱台):就是__________________的面积的和。
旋转体:(1)圆柱
=________________
=
____________
____________
圆锥
=________________
=
____________
____________
圆台=
=
____________
____________
体积公式
柱体:V=
__________
椎体:V=
__________
台体:V=_________________
思考:你能发现柱体、椎体、台体三者的体积公式之间的关系吗?
例1.已知圆柱和圆锥的高、底面半径均分别相等。若圆柱的底面半径为
( http: / / www.21cnjy.com ),圆柱侧面积为S,求圆锥的侧面积。
变式训练:若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为(
)
A.
( http: / / www.21cnjy.com )B.
( http: / / www.21cnjy.com )C.
( http: / / www.21cnjy.com )
D.
( http: / / www.21cnjy.com )
例2.如果一个空间几何体的正视图与侧视图均为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的体积为(
)
A.
( http: / / www.21cnjy.com )
B.
( http: / / www.21cnjy.com )
C.
( http: / / www.21cnjy.com )
D.
( http: / / www.21cnjy.com )
变式训练:
如图所示,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为(
)
A.1
B.
( http: / / www.21cnjy.com )
C.
( http: / / www.21cnjy.com )
D.
( http: / / www.21cnjy.com )
课后练习与提高
1.如图所示,圆锥的底面半径为1,高为
( http: / / www.21cnjy.com ),则圆锥的
表面积为(
)
( http: / / www.21cnjy.com )
B.
( http: / / www.21cnjy.com )
C.
( http: / / www.21cnjy.com )
D.
( http: / / www.21cnjy.com )
2.正三棱锥的底面边长为3,侧棱长为
( http: / / www.21cnjy.com ),则这个正三棱锥的体积是(
)
A.
( http: / / www.21cnjy.com )
B.
( http: / / www.21cnjy.com )
C.
( http: / / www.21cnjy.com )
D.
( http: / / www.21cnjy.com )
3.已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是(
)
A.
( http: / / www.21cnjy.com )
B.
( http: / / www.21cnjy.com )
C.
( http: / / www.21cnjy.com )
D.
( http: / / www.21cnjy.com )
4.三棱锥
( http: / / www.21cnjy.com )的中截面是
( http: / / www.21cnjy.com ),则三棱锥
( http: / / www.21cnjy.com )与三棱锥
( http: / / www.21cnjy.com )的体积之比是(
)A.1:2
B.1:4
C.1:6
D.1:8
5.若圆柱的高扩大为原来的4倍,底面半径不变,则圆柱的体积扩大为原来的
倍;若圆柱的高不变,底面半径扩大为原来的4倍,则圆柱的体积扩大为原来的
倍。
6.已知一圆锥的侧面展开图为半圆,且面积为S,则圆锥的底面面积是
。
7.右图是一个正方体,H、G、F分别是棱AB、AD、
( http: / / www.21cnjy.com )的中点。现在沿
( http: / / www.21cnjy.com )所在平面锯掉正方体的一个角,问锯掉部分的体积是原正方体体积的几分之几?
1.
3.2
球的体积和表面积
【教学目标】
(1)能运用球的面积和体积公式灵活解决实际问题。
(2)培养学生的空间思维能力和空间想象能力。
【教学重难点】
重点:球的体积和面积公式的实际应用
难点:应用体积和面积公式中空间想象能力的形成。
【教学过程】
球的大小是与球的半径有关,如何用球半径来表示球的体积和面积?
球的体积和面积公式:半径是R的球的体积V=
,表面积S=
例1.一种空心钢球的质量是732πg,外径是5cm,求它的内径.
(钢密度9g/cm3)
求空心钢球的体积
。
变式:正方体的棱长为2,顶点都在同一球面上,则球的体积为____________
例2
在球心同侧有相距9的两个平行截面,它们的面积分别为49π和400π,求球的表面积。
变式:长方体的一个顶点上三条棱长分别为3、4、5,是它的八个顶点都在同一球面上,则这个球的表面积是
。
课后练习与提高
1、将气球的半径扩大1倍,它的体积增大到原来的()倍
A2
B4
C8
D16
2.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是(
)
A.16π
B.20π
C.24π
D.32π
3.三个球的半径之比为1∶2∶3,那么最大球的表面积是其余两个球的表面积之和的(
)
A.1倍
B.2倍
C.
( http: / / www.21cnjy.com )倍
D.
( http: / / www.21cnjy.com )倍.
4.若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为____________.
5.一个球与正四面体的六条棱都相切,若正四面体的棱长为a,则这个球的体积为_____________..
6、若三个球的表面积之比是1:2:3,则它们的体积之比是_____________..
7、用与球心距离为2的平面去截球,若球的体积为36,截面圆的面积_____.
一个直径为32cm的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9cm,求此球的半径。
9、
下图是一个底面直径为20
cm的装
( http: / / www.21cnjy.com )有一部分水的圆柱形玻璃杯,水中放着一个底面直径为6
cm,高为20
cm的一个圆锥形铅锤,当铅锤从水中取出后,杯里的水将下降几厘米?
( http: / / www.21cnjy.com )
综合练习:1、已知一几何体的三视图如下图,试求其表面积与体积.
2、已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形
( http: / / www.21cnjy.com ).
(1)求该几何体的体积V;
(2)求该几何体的侧面积S
