广东省深圳市平湖实验学校2016届高考数学(文)查漏补缺练习题(解析版)
文档属性
| 名称 | 广东省深圳市平湖实验学校2016届高考数学(文)查漏补缺练习题(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-02 00:00:00 | ||
图片预览



文档简介
www.
2016年高考文科数学查漏补缺练习题
1.
在等差数列{an}中,已知公差d=2,
a2是a1
与a4
的等比中项.
(1)求数列
{an}的通项公式;
(2)设
,记
Tn=-b1+b2-b3+b4-…+(-1)nbn,求Tn
.
2.已知等差数列{an}满足a2=3,a7=13,
Sn表示{an}的前n项和.
(1)求an及Sn;
(2)设{bn}是首项为2的等比数列,公比q满足q2-(a4+1)q+S4=0,求{bn}的通项公式及其前n
项和Tn.
3.在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列.
(1)求d,an;
(2)
若d<0,求|a1|+|a2|+|a3|+…+|an|.
4.数列{an}
满足a1=1,nan+1=(n+1)an+n(n+1),n∈N
.
(1)证明:数列是等差数列;
(2)设
bn=3n·,求数列{bn}的前
n项和
Sn.
5.已知数列{an}
的前n
项和Sn=,n∈N
.
(1)求数列{an}
的通项公式;
(2)设bn=2an+(-1)nan
,求数列{bn}
的前2n
项和.
6.
设各项均为正数的数列{an}
的前n
项和为Sn
,且
Sn满足
S-(n2+n-3)Sn-3(n2+n)=0,n∈N
.
(1)
求数列{an}
的通项公式;
(2)设,为数列{bn}的前n
项和,证明:对一切正整数n
,有.
7.
如图,在平面四边形中,,,,,.
(Ⅰ)求;
(Ⅱ)求的长.
8.内角的对边分别是,函数=,在处取得最大值。
(I)
当,求函数的值域;
(Ⅱ)若a=7,且,求的面积。
9.
中,已知,D是BC边上的一点
若AD=2,,求CD的长
若AB=AD,试求的最大值
10.
已知分别是内角的对边,且.
(I)求的值;
(II)若,,求的面积.
11.为了整顿道路交通秩序,某地考虑对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通人中随机抽取理200人进行调查,当不处罚时,由80人会闯红灯,处罚时,得到如下数据:
处罚金额(单位:元)
5
10
15
20
会闯红灯的人数
50
40
20
0
若用表中数据所得频率代替概率.
(Ⅰ)当处罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(Ⅱ)将选取的200人中会闯红灯的市民分为两类:类市民在罚金不超过10元时就会改正行为;类是其它市民.现对类与类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为类市民的概率是多少?
12.某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题。
(I)求分数在[70,80)内的频率;
(Ⅱ)从频率分布直方图中,估计本次考试成绩的中位数;
(III)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率。
13.某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
(Ⅰ)根据以上资料完成下面的2×2列联表,若据此数据算得,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?
不满意
满意
合计
男
4
7
女
合计
附:
P(K2≥k)
0.100
0.050
0.010
k
2.706
3.841
6.635
(Ⅱ)
估计用户对该公司的产品“满意”的概率;
(Ⅲ)
该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
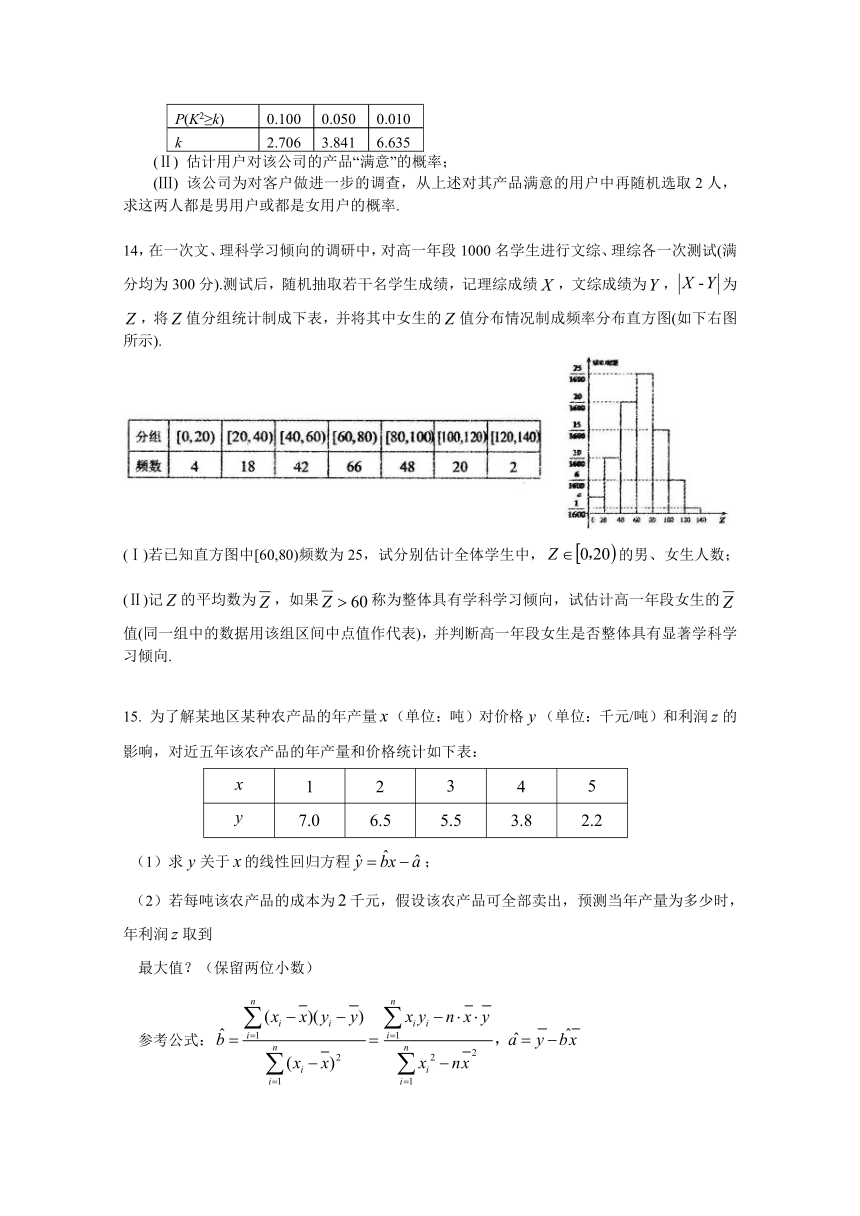
14,在一次文、理科学习倾向的调研中,对高一年段1000名学生进行文综、理综各一次测试(满分均为300分).测试后,随机抽取若干名学生成绩,记理综成绩,文综成绩为,为,将值分组统计制成下表,并将其中女生的值分布情况制成频率分布直方图(如下右图所示).
(Ⅰ)若已知直方图中[60,80)频数为25,试分别估计全体学生中,的男、女生人数;
(Ⅱ)记的平均数为,如果称为整体具有学科学习倾向,试估计高一年段女生的值(同一组中的数据用该组区间中点值作代表),并判断高一年段女生是否整体具有显著学科学习倾向.
15.
为了解某地区某种农产品的年产量(单位:吨)对价格(单位:千元/吨)和利润的影响,对近五年该农产品的年产量和价格统计如下表:
(1)求关于的线性回归方程;
(2)若每吨该农产品的成本为千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润取到
最大值?(保留两位小数)
参考公式:
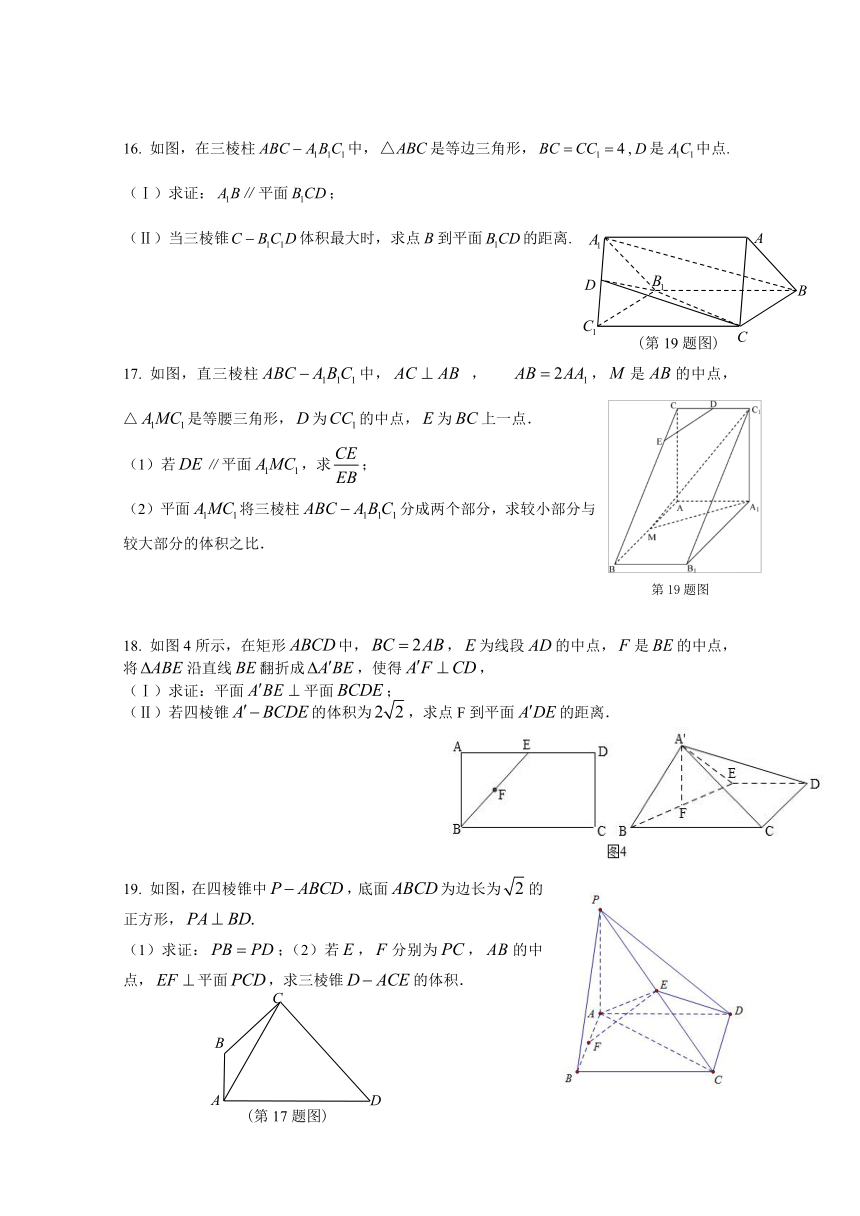
16.
如图,在三棱柱中,是等边三角形,,是中点.
(Ⅰ)求证:平面;
(Ⅱ)当三棱锥体积最大时,求点到平面的距离.
17.
如图,直三棱柱中,
,
,是的中点,△是等腰三角形,为的中点,为上一点.
(1)若∥平面,求;
(2)平面将三棱柱分成两个部分,求较小部分与较大部分的体积之比.
18.
如图4所示,在矩形中,,为线段的中点,是的中点,将沿直线翻折成,使得,
(Ⅰ)求证:平面平面;
(Ⅱ)若四棱锥的体积为,求点F到平面的距离.
19.
如图,在四棱锥中,底面为边长为的正方形,
(1)求证:;(2)若,分别为,的中点,平面,求三棱锥的体积.
20
如图,三棱柱中,,,.
(Ⅰ)证明:;
(Ⅱ)若,
,求三棱锥的体积.
21已知圆,若椭圆的右顶点为圆M的圆心,离心率为.
(1)求椭圆C的方程;
(2)已知直线,若直线与椭圆C分别交于A,B两点,与圆M分别交于G,H两点(其中点G在线段AB上),且,求的值.
22.如图,在平面直角坐标系中,已知是椭圆上的一点,从原点向圆作两条切线,分别交椭圆于点.
(1)若点在第一象限,且直线互相垂直,求圆的方程;
(2)若直线的斜率存在,并记为,求的值。
23.如图,已知以点为圆心的圆与直线相切,过点的动直线与圆相交于,两点,是的中点,直线与相交于点.
(Ⅰ)求圆的方程;
(Ⅱ)当时,求直线的方程;
(Ⅲ)是否为定值?如果是,求出该
定值;如果不是,说明理由.
24.已知抛物线:过点,其焦点为,且.
(Ⅰ)求抛物线的方程;
(Ⅱ)设为轴上异于原点的任意一点,过点作不经过原点的两条直线分别与抛物线和圆:相切,切点分别为,求证:、、三点共线.
25.已知函数,.
(1)当,时,求的单调区间;
(2)当,且
时,求在区间上的最大值.
26.已知函数
x轴为曲线
的切线;
求a的值;
当时,,求实数的取值范围。
27.
已知函数.
(1)若函数的图象在处的切线与轴平行,求的值;
(2)若时,恒成立,求的取值范围.
28.已知定义在上的函数.
(1)求此函数的单调区间;
(2)若过点有且仅有一条直线与函数的图象相切,求的取值范围.
选做题:
1.极坐标系与直角坐标系有相同的长度单位,以原点为极点,以轴正半轴为极轴.已知直线的参数方程为(为参数),曲线的极坐标方程为.
(1)求的直角坐标方程;
(2)设直线与曲线交于两点,求弦长.
2.在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acos
θ(a>0),过点P(-2,-4)的直线l:(t为参数)与曲线C相交于M,N两点.
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求实数a的值.
3.已知在直角坐标系中,圆的参数方程为(为参数).
(1)以原点为极点、轴正半轴为极轴建立极坐标系,求圆的极坐标方程;
(2)已知,圆上任意一点,求△面积的最大值.
4.已知曲线:
(为参数),
:(为参数).
(1)化,的方程为普通方程,并说明它们分别表示什么曲线;
(2)若上的点对应的参数为,为上的动点,求中点到直线
(为参数)距离的最小值.
5.已知直线:(为参数, 为的倾斜角),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线为:.
(1)若直线与曲线相切,求的值;
(2)设曲线上任意一点的直角坐标为,求的取值范围.
6.在直角坐标系xOy中,圆C的参数方程为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线的极坐标方程是,射线与圆C的交点为O,P,与直线的交点为Q,求线段PQ的长.
参考答案
1解:(1)由题意知(a1+d)2=a1(a1+3d),
即(a1+2)2=a1(a1+6),解得a1=2.
所以数列{an}的通项公式为an=2n.
(2)由题意知.
所以Tn=-1×2+2×3-3×4+…+(-1)nn×(n+1).
因为bn+1-bn=2(n+1),
可得当n为偶数时,Tn=(-b1+b2)+(-b3+b4)+…+(-bn-1+bn)
=4+8+12+…+2n==,
当n为奇数时,Tn=Tn-1+(-bn)=-n(n+1)=-.
所以Tn=
2解:(1)设等差数列{an}的首项a1,公差d,则
所以an=a1+(n-1)d=2n-1.
故Sn=1+3+…+(2n-1)===n2.
(2)由(1)得a4=7,S4=16.因为q2-(a4+1)q+S4=0,即q2-8q+16=0,
所以(q-4)2=0,从而q=4.
又因b1=2,{bn}是公比q=4的等比数列,
所以bn=b1qn-1=2·4n-1=22n-1.
从而{bn}的前n项和Tn==(4n-1).
3解:
(1)由题意得5a3·a1=(2a2+2)2,
即d2-3d-4=0.故d=-1或d=4.
所以an=-n+11,n∈N
或an=4n+6,n∈N
.
(2)设数列{an}的前n项和为Sn.因为d<0,由(1)得d=-1,an=-n+11.则
当n≤11时,|a1|+|a2|+|a3|+…+|an|=Sn=-n2+n.
当n≥12时,|a1|+|a2|+|a3|+…+|an|=-Sn+2S11=n2-n+110.
综上所述,
|a1|+|a2|+|a3|+…+|an|=
4解:(1)证明:由已知可得=+1,即-=1.
所以是以=1为首项,1为公差的等差数列.
(2)由(1)得=1+(n-1)·1=n,所以an=n2.从而bn=n·3n.
Sn=1·31+2·32+3·33+…+n·3n,①
3Sn=1·32+2·33+…+(n-1)·3n+n·3n+1.②
①-②得-2Sn=31+32+…+3n-n·3n+1=-n·3n+1=.
所以Sn=.
5解:(1)当n=1时,a1=S1=1;
当n≥2时,an=Sn-Sn-1=-=n.
故数列{an}的通项公式为an=n.
(2)由(1)知,an=n,故bn=2n+(-1)nn.记数列{bn}的前2n项和为T2n,
则T2n=(21+22+…+22n)+(-1+2-3+4-…+2n).
记A=21+22+…+22n,B=-1+2-3+4-…+2n,则
A==22n+1-2,B=(-1+2)+(-3+4)+…+[-(2n-1)+2n]=n.
故数列{bn}的前2n项和T2n=A+B=22n+1+n-2.
6解:(1)由S-(n2+n-3)Sn-3(n2+n)=0,n∈N
可得,(Sn+3)(Sn-n2-n)=0,
则Sn=n2+n或Sn=-3,
又数列{an}的各项均为正数,所以Sn=n2+n,Sn-1=(n-1)2+(n-1),
所以当n≥2时,an=Sn-Sn-1=n2+n-[(n-1)2+(n-1)]=2n.
又a1=2=2×1,所以an=2n.
(2)当n=1时,,有成立;
当n≥2时,,
所以
,
又因为时,单调递增.
所以对一切正整数n,有.
7.(Ⅰ)在中,由余弦定理得:,
即,解得:,或(舍),
………………3分
由正弦定理得:
………………6分
(Ⅱ)由(Ⅰ)有:,,
所以,
………………9分
由正弦定理得:……………12分
在处取得最大值
,AD=2
由正弦定理得
10解:(I)∵、为的内角,
由知,结合正弦定理可得:
------------------------------------------------------------3分
,-----------------------------------------------------------------4分
∵
∴.--------------------------------------------------------5分
(II)解法1:∵,,
由余弦定理得:,----------------------------------------7分
整理得:
解得:或(不合舍去)--------------------------9分
∴,由得
的面积.--------------------------------------12分
【解法2:由结合正弦定理得:,---------------------6分
∵,
∴,
∴,-----------------------------7分
∴
=----------------------------9分
由正弦定理得:,-------------------------------------------------10分
∴的面积.------------------------------------12分】
11解:⑴设“当罚金定为10元时,闯红灯的市民改正行为”为事件,……2分
则………………………4分
∴当罚金定为10元时,比不制定处罚,行人闯红灯的概率会降低.……………6分
⑵由题可知类市民和类市民各有40人,故分别从类市民和类市民各抽出两人,设从类市民抽出的两人分别为、,设从类市民抽出的两人分别为、.
设从“类与类市民按分层抽样的方法抽取4人依次进行深度问卷”为事件,
………………………8分
则事件中首先抽出的事件有:,
,
,,共6种.
同理首先抽出、、的事件也各有6种.
故事件共有种.………………………10分
设从“抽取4人中前两位均为类市民”为事件,则事件有,
,,.
∴抽取4人中前两位均为类市民的概率是.………………………12分
12解(Ⅰ)分数在[70,80)内的频率为1-(0.010+0.015+0.015+0.025+0.005)×10=0.3,…2分
(Ⅱ)由频率频率分布直方图知前三组的频率之和为0.1+0.15+0.15=0.4,…………………3分
∴中位数在第四组,设中位数为70+x,则0.4+0.030×x=0.5 x=…………………4分
∴数据的中位数为70+=…………………5分
(Ⅲ)第1组有60×0.1=6人(设为1,2,3,4,5,6)
第6组有60×0.05=3人(设为A,B,C)…………………7分
从9人中任取2人有
共36种方法;…………………9分
其中抽取2人成绩之差的绝对值大于10的抽法是从第1组与第6组各抽取1人,抽法有
共18种,…………………11分
∴抽取2人成绩之差的绝对值大于10的概率为…………………12分
13解:(Ⅰ)
不满意
满意
合计
男
3
4
7
女
11
2
13
合计
14
6
20
-----------------------------2分
∵<3.84
1,
∴在犯错的概率不超过5%的前提下,不能认为“满意与否”与“性别”有关。-----------4分
(Ⅱ)因样本20人中,对该公司产品满意的有6人,故估计用户对该公司的产品“满意”的概率为,------------------------------------------------------------------6分
(Ⅲ)由(Ⅰ)知,对该公司产品满意的用户有6人,其中男用户4人,女用户2人,
设男用户分别为;女用户分别为,--------------------------------------8分
从中任选两人,记事件A为“选取的两个人都是男用户或都是女用户”,则
总的基本事件为
共15个,----------------------------------10分
而事件A包含的基本事件为共7个,
故.----------------------------------------------------------------12分
14解:(Ⅰ)由频率分布直方图可知,女生的频率为.
………1分
所以样本中女生总人数为.
………2分
由频率分布直方图可知,女生的频率为
,
…………4分
所以女生的频数为.
结合统计表可知,男生的频数为.
………6分
又因为样本容量为,故样本中,男、女生的频率分别为与,
…………7分
据频率估计概率、样本估计总体的统计思想,可知年段名学生中,的男生约有名,女生约有名.………8分
(Ⅱ)依题意,样本中女生的值约为
.10分
根据样本估计总体的统计思想,全体女生.
…………11分
因为,所以年段女生整体具有显著学科学习倾向.
…………12分
15解:(1),…………2分
错误!未找到引用源。………………4分
…………………6分
…………………7分
关于的线性回归方程是…………………8分
(2)年利润
…………………10分
…………………11分
所以当时,年利润最大.…………………12分
16解:(Ⅰ)连结,交于,连.
在三棱柱中,四边形为平行四边形,则,又是中点,
∴,而平面,平面,∴平面.
………4分
(Ⅱ)设点到平面的距离是,则,而,故当三棱锥体积最大时,,即平面.
……………6分
由(Ⅰ)知:,所以到平面的距离与到平面的距离相等.
∵平面,平面,∴,
∵是等边三角形,是中点,∴,又,平面,平面,∴平面,∴,由计算得:,所以,…9分
设到平面的距离为,由得:,所以到平面的距离是
……………12分
17解:
取中点为,连结,………1分
∵分别为中点
∴∥∥,
∴四点共面,
………3分
且平面平面
又平面,且∥平面
∴∥
∵为的中点,
∴是的中点,
………5分
∴.
………6分
(2)因为三棱柱为直三棱柱,∴平面,
又,则平面
设,又三角形是等腰三角形,所以.
方法一:如图,将几何体补成三棱柱
∴几何体的体积为:
………9分
又直三棱柱体积为:
………11分
故剩余的几何体棱台的体积为:
∴较小部分的体积与较大部分体积之比为:.
………12分
方法二:(分割)
几何体的体积为:
又直三棱柱体积为:
………11分
故剩余的几何体棱台的体积为:
∴较小部分的体积与较大部分体积之比为:.
………12分
18证明:(Ⅰ)∵,为线段的中点,
∴,,------------------------------------1分
故在四棱锥中,
又∵,且、为相交直线,
∴平面,---------------------------------------3分
又平面,∴平面平面;-------------5分
(Ⅱ)设,则,,
在等腰直角中,,;--------6分
由(Ⅰ)知是四棱锥的高,
故,
整理得,∴,--------------------------8分
连结,在中,由余弦定理可求得,
于是,
∵
为等腰三角形,其面积;------10分
设点F到平面的距离为,因,
由
所以点F到平面的距离为-------------------12分
19解:(1)连接,,,交于点,
∵底面是正方形,∴且为的中点.……2分
又∵,,∴平面.……4分
由于平面,故.
又∵,故;………………5分
(2)设的中点为,连接,,则,
∴为平行四边形,.………………(7分)
∵平面,∴平面,∴.
∵的中点为,∴.
由平面,可得,………………(9分)
又∵,,∴平面,∴.………………(10分)
又∵,∴平面,
∴,
故三棱锥的体积为.………………(12分)
20解析:(Ⅰ)证明:取的中点,连接,,.
,,………………………………………….
2分
又,.
为等边三角形.
,………….…….3分
又因为平面,平面,
.
平面.………………………………………..………….5分
又平面,因此;…………………………….6分
(Ⅱ)解:在等边中,在等边中;
在中.
是直角三角形,且,故.……….….8分
由(Ⅰ)得
又平面,平面,,
平面.
故是三棱锥的高.……………………………..…………….9分
又.
……………….12分
21解:(1)圆M的圆心为,则
,,故
椭圆C的方程为
(2)设,,由直线与椭圆C交于两点A,B
则
得
所以,
点M到直线的距离,则
显然,若点H也在线段AB上,则由对称性可知,直线就是y轴,矛盾
,
即,
解得,即
22解:(1)由圆的方程知圆的半径,因为直线互相垂直,且和圆相切,所以,即
①
又点在椭圆上,所以
②
联立①②,解得,
所以,所求圆的方程为
.
(2)因为直线和都与圆相切,所以,,
化简得,
因为点在椭圆上,所以,即,
所以.
23解:(Ⅰ)设圆A的半径为R,则
圆A的方程为
(II)当直线与x轴垂直时,易知符合题意;
当直线与x轴不垂直时,设直线的方程为,
连接,则
∵,∴
由,得,∴直线的方程为
(III)∵,∴=
当直线与x轴垂直时,得∴
当直线的斜率存在时,由,解得
∴
∴,∴是定值-5.
24解:(I)抛物线的准线方程为:,
,又,即……………2分
抛物线的方程为.
……………4分
(II)设,已知切线不为轴,设
联立,消去,可得
直线与抛物线相切,,即
代入,,即
……………………6分
设切点,则由几何性质可以判断点关于直线对称,则
,解得:,即……………………8分
直线的斜率为,
直线的斜率为,
,即三点共线.
……………………………………10分
当时,,此时共线.
综上:三点共线.
……………………………………12分
25解:(1)当,时,,
……………………………1分则
……………………………2分
令,解得,,
当或时,有;
当时,有,…………
5分
所以的单调递增区间和,的单调递减区间.
……………………………7分
(2)当,且
时,,.
则,
令,得或.
…………………8分
①当,即时,
此时当时,有,所以在上为减函数,
当时,有,所以在上为增函数,
………9分
又,,
所以的最大值为;
…………………………10分
②当,即时,
此时当时,;当时,;当时,;所以在上为增函数,在上为减函数,在上为增函数.
……………………12分
,
,
所以的最大值为,
…………………13分
综上,在区间上的最大值为
.
…………………14分
26解:(Ⅰ)设曲线与轴相切于点,则,,即,解得.
因此,当时,轴是曲线的切线.
(II)解法1:,整理得
∵,,且等号不能成立,∴
∴等价于恒成立,令
,其中,∴
又因为,所以
∴函数在区间上单调递增,,
∴
解法2.
,整理得
即,令
①当,即时,,故在区间上单调递增,
,∴
②当,即时,,故在区间上单调递减,
,∴解得,
∴此种情况不符合题意
③当时,,
其中,,,∴,∴此种情况不符合题意
综上,
27解:⑴,
…………2分
,即:
.
………
4分
⑵令,
对恒成立
在内单调递增,且
………6分
①当,即时,
在上为增函数
………8分
②当,即时,
由在内单调递增知:
存在唯一,使得,即.
令,得,,得;
………
10分
,即.
由①易知函数单减,故
综上,实数的取值范围是.
………
12分
28解:(1)由题意......................1分
当时,函数在上是减函数,
当时,此时函数在上是减函数,在上是增函数,
当时,函数在上是增函数..................................4分
(2)设切点,
∴切线的斜率.......................................5分
即:,
即:,
所以过点有且仅有一条直线与函数的图象相切等价于方程
在定义域上有且只有一个解;................6分
令,则在上有且只有一个零点;
设.......................7分
①当时,在单减,在单增,最小值,在上恒正,在上恒正,不符合条件;
②当时,,在为增函数,,
此时在上恒正,不符合条件;
③当时,在为增函数,,此时在上恒正,不符合条件;
④当时,在为增函数,,
当
当,即:时,
上恰有一个零点;不符合条件;
综上:.............................................12分
选做题参考答案:
1解:(1)由,得,即曲线的直角坐标方程为.
(2)方法一:
将直线的方程代入,并整理得,,.
所以.
方法二:弦长公式
直线的普通方程;
设直线交曲线于,则
,消去得,,,;
所以,直线被曲线截得的线段的长为.
2解:(1)把代入ρsin2θ=2acos
θ,得y2=2ax(a>0),
(t为参数),消去t得x-y-2=0,
∴曲线C的直角坐标方程和直线l的普通方程分别是y2=2ax(a>0),x-y-2=0.
(2)将(t为参数)代入y2=2ax,整理得t2-2(4+a)t+8(4+a)=0.
设t1,t2是该方程的两根,则t1+t2=2(4+a),t1·t2=8(4+a),
∵|MN|2=|PM|·|PN|,∴(t1-t2)2=(t1+t2)2-4t1·t2=t1·t2,
∴8(4+a)2-4×8(4+a)=8(4+a),
∴a=1.
3解:(1)圆的参数方程为(为参数)
所以普通方程为
圆的极坐标方程:
(2)点到直线:的距离为
△的面积
所以△面积的最大值为。
4解:(1),
所以为圆心是,半径是1的圆.
为中心是坐标原点,焦点在轴上,长半轴长是8,短半轴长是3的椭圆.
(2)
当时,,
设,则,
为直线,
到的距离
(其中),所以,d的最小值是
5解:(1)曲线C的直角坐标方程为
即
曲线C为圆心为(3,0),半径为2的圆.
直线l的方程为:
∵直线l与曲线C相切
∴
,即
∵
[0,π)
∴ =
(2)设,
则,
的取值范围是.
6解:(1)圆的普通方程是,又;
所以圆的极坐标方程是.
(2)设为点的极坐标,则有
,
解得.
设为点的极坐标,则有
解得
由于,所以,所以线段的长为2.
3
3
4
6
8
5
1
3
6
4
6
2
4
5
5
1
7
3
3
5
6
9
8
3
2
1
图3
A
B
C
D
(第19题图)
第19题图
A
C
D
B
(第17题图)
O
D
2016年高考文科数学查漏补缺练习题
1.
在等差数列{an}中,已知公差d=2,
a2是a1
与a4
的等比中项.
(1)求数列
{an}的通项公式;
(2)设
,记
Tn=-b1+b2-b3+b4-…+(-1)nbn,求Tn
.
2.已知等差数列{an}满足a2=3,a7=13,
Sn表示{an}的前n项和.
(1)求an及Sn;
(2)设{bn}是首项为2的等比数列,公比q满足q2-(a4+1)q+S4=0,求{bn}的通项公式及其前n
项和Tn.
3.在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列.
(1)求d,an;
(2)
若d<0,求|a1|+|a2|+|a3|+…+|an|.
4.数列{an}
满足a1=1,nan+1=(n+1)an+n(n+1),n∈N
.
(1)证明:数列是等差数列;
(2)设
bn=3n·,求数列{bn}的前
n项和
Sn.
5.已知数列{an}
的前n
项和Sn=,n∈N
.
(1)求数列{an}
的通项公式;
(2)设bn=2an+(-1)nan
,求数列{bn}
的前2n
项和.
6.
设各项均为正数的数列{an}
的前n
项和为Sn
,且
Sn满足
S-(n2+n-3)Sn-3(n2+n)=0,n∈N
.
(1)
求数列{an}
的通项公式;
(2)设,为数列{bn}的前n
项和,证明:对一切正整数n
,有.
7.
如图,在平面四边形中,,,,,.
(Ⅰ)求;
(Ⅱ)求的长.
8.内角的对边分别是,函数=,在处取得最大值。
(I)
当,求函数的值域;
(Ⅱ)若a=7,且,求的面积。
9.
中,已知,D是BC边上的一点
若AD=2,,求CD的长
若AB=AD,试求的最大值
10.
已知分别是内角的对边,且.
(I)求的值;
(II)若,,求的面积.
11.为了整顿道路交通秩序,某地考虑对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通人中随机抽取理200人进行调查,当不处罚时,由80人会闯红灯,处罚时,得到如下数据:
处罚金额(单位:元)
5
10
15
20
会闯红灯的人数
50
40
20
0
若用表中数据所得频率代替概率.
(Ⅰ)当处罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(Ⅱ)将选取的200人中会闯红灯的市民分为两类:类市民在罚金不超过10元时就会改正行为;类是其它市民.现对类与类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为类市民的概率是多少?
12.某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题。
(I)求分数在[70,80)内的频率;
(Ⅱ)从频率分布直方图中,估计本次考试成绩的中位数;
(III)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率。
13.某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
(Ⅰ)根据以上资料完成下面的2×2列联表,若据此数据算得,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?
不满意
满意
合计
男
4
7
女
合计
附:
P(K2≥k)
0.100
0.050
0.010
k
2.706
3.841
6.635
(Ⅱ)
估计用户对该公司的产品“满意”的概率;
(Ⅲ)
该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
14,在一次文、理科学习倾向的调研中,对高一年段1000名学生进行文综、理综各一次测试(满分均为300分).测试后,随机抽取若干名学生成绩,记理综成绩,文综成绩为,为,将值分组统计制成下表,并将其中女生的值分布情况制成频率分布直方图(如下右图所示).
(Ⅰ)若已知直方图中[60,80)频数为25,试分别估计全体学生中,的男、女生人数;
(Ⅱ)记的平均数为,如果称为整体具有学科学习倾向,试估计高一年段女生的值(同一组中的数据用该组区间中点值作代表),并判断高一年段女生是否整体具有显著学科学习倾向.
15.
为了解某地区某种农产品的年产量(单位:吨)对价格(单位:千元/吨)和利润的影响,对近五年该农产品的年产量和价格统计如下表:
(1)求关于的线性回归方程;
(2)若每吨该农产品的成本为千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润取到
最大值?(保留两位小数)
参考公式:
16.
如图,在三棱柱中,是等边三角形,,是中点.
(Ⅰ)求证:平面;
(Ⅱ)当三棱锥体积最大时,求点到平面的距离.
17.
如图,直三棱柱中,
,
,是的中点,△是等腰三角形,为的中点,为上一点.
(1)若∥平面,求;
(2)平面将三棱柱分成两个部分,求较小部分与较大部分的体积之比.
18.
如图4所示,在矩形中,,为线段的中点,是的中点,将沿直线翻折成,使得,
(Ⅰ)求证:平面平面;
(Ⅱ)若四棱锥的体积为,求点F到平面的距离.
19.
如图,在四棱锥中,底面为边长为的正方形,
(1)求证:;(2)若,分别为,的中点,平面,求三棱锥的体积.
20
如图,三棱柱中,,,.
(Ⅰ)证明:;
(Ⅱ)若,
,求三棱锥的体积.
21已知圆,若椭圆的右顶点为圆M的圆心,离心率为.
(1)求椭圆C的方程;
(2)已知直线,若直线与椭圆C分别交于A,B两点,与圆M分别交于G,H两点(其中点G在线段AB上),且,求的值.
22.如图,在平面直角坐标系中,已知是椭圆上的一点,从原点向圆作两条切线,分别交椭圆于点.
(1)若点在第一象限,且直线互相垂直,求圆的方程;
(2)若直线的斜率存在,并记为,求的值。
23.如图,已知以点为圆心的圆与直线相切,过点的动直线与圆相交于,两点,是的中点,直线与相交于点.
(Ⅰ)求圆的方程;
(Ⅱ)当时,求直线的方程;
(Ⅲ)是否为定值?如果是,求出该
定值;如果不是,说明理由.
24.已知抛物线:过点,其焦点为,且.
(Ⅰ)求抛物线的方程;
(Ⅱ)设为轴上异于原点的任意一点,过点作不经过原点的两条直线分别与抛物线和圆:相切,切点分别为,求证:、、三点共线.
25.已知函数,.
(1)当,时,求的单调区间;
(2)当,且
时,求在区间上的最大值.
26.已知函数
x轴为曲线
的切线;
求a的值;
当时,,求实数的取值范围。
27.
已知函数.
(1)若函数的图象在处的切线与轴平行,求的值;
(2)若时,恒成立,求的取值范围.
28.已知定义在上的函数.
(1)求此函数的单调区间;
(2)若过点有且仅有一条直线与函数的图象相切,求的取值范围.
选做题:
1.极坐标系与直角坐标系有相同的长度单位,以原点为极点,以轴正半轴为极轴.已知直线的参数方程为(为参数),曲线的极坐标方程为.
(1)求的直角坐标方程;
(2)设直线与曲线交于两点,求弦长.
2.在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acos
θ(a>0),过点P(-2,-4)的直线l:(t为参数)与曲线C相交于M,N两点.
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求实数a的值.
3.已知在直角坐标系中,圆的参数方程为(为参数).
(1)以原点为极点、轴正半轴为极轴建立极坐标系,求圆的极坐标方程;
(2)已知,圆上任意一点,求△面积的最大值.
4.已知曲线:
(为参数),
:(为参数).
(1)化,的方程为普通方程,并说明它们分别表示什么曲线;
(2)若上的点对应的参数为,为上的动点,求中点到直线
(为参数)距离的最小值.
5.已知直线:(为参数, 为的倾斜角),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线为:.
(1)若直线与曲线相切,求的值;
(2)设曲线上任意一点的直角坐标为,求的取值范围.
6.在直角坐标系xOy中,圆C的参数方程为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线的极坐标方程是,射线与圆C的交点为O,P,与直线的交点为Q,求线段PQ的长.
参考答案
1解:(1)由题意知(a1+d)2=a1(a1+3d),
即(a1+2)2=a1(a1+6),解得a1=2.
所以数列{an}的通项公式为an=2n.
(2)由题意知.
所以Tn=-1×2+2×3-3×4+…+(-1)nn×(n+1).
因为bn+1-bn=2(n+1),
可得当n为偶数时,Tn=(-b1+b2)+(-b3+b4)+…+(-bn-1+bn)
=4+8+12+…+2n==,
当n为奇数时,Tn=Tn-1+(-bn)=-n(n+1)=-.
所以Tn=
2解:(1)设等差数列{an}的首项a1,公差d,则
所以an=a1+(n-1)d=2n-1.
故Sn=1+3+…+(2n-1)===n2.
(2)由(1)得a4=7,S4=16.因为q2-(a4+1)q+S4=0,即q2-8q+16=0,
所以(q-4)2=0,从而q=4.
又因b1=2,{bn}是公比q=4的等比数列,
所以bn=b1qn-1=2·4n-1=22n-1.
从而{bn}的前n项和Tn==(4n-1).
3解:
(1)由题意得5a3·a1=(2a2+2)2,
即d2-3d-4=0.故d=-1或d=4.
所以an=-n+11,n∈N
或an=4n+6,n∈N
.
(2)设数列{an}的前n项和为Sn.因为d<0,由(1)得d=-1,an=-n+11.则
当n≤11时,|a1|+|a2|+|a3|+…+|an|=Sn=-n2+n.
当n≥12时,|a1|+|a2|+|a3|+…+|an|=-Sn+2S11=n2-n+110.
综上所述,
|a1|+|a2|+|a3|+…+|an|=
4解:(1)证明:由已知可得=+1,即-=1.
所以是以=1为首项,1为公差的等差数列.
(2)由(1)得=1+(n-1)·1=n,所以an=n2.从而bn=n·3n.
Sn=1·31+2·32+3·33+…+n·3n,①
3Sn=1·32+2·33+…+(n-1)·3n+n·3n+1.②
①-②得-2Sn=31+32+…+3n-n·3n+1=-n·3n+1=.
所以Sn=.
5解:(1)当n=1时,a1=S1=1;
当n≥2时,an=Sn-Sn-1=-=n.
故数列{an}的通项公式为an=n.
(2)由(1)知,an=n,故bn=2n+(-1)nn.记数列{bn}的前2n项和为T2n,
则T2n=(21+22+…+22n)+(-1+2-3+4-…+2n).
记A=21+22+…+22n,B=-1+2-3+4-…+2n,则
A==22n+1-2,B=(-1+2)+(-3+4)+…+[-(2n-1)+2n]=n.
故数列{bn}的前2n项和T2n=A+B=22n+1+n-2.
6解:(1)由S-(n2+n-3)Sn-3(n2+n)=0,n∈N
可得,(Sn+3)(Sn-n2-n)=0,
则Sn=n2+n或Sn=-3,
又数列{an}的各项均为正数,所以Sn=n2+n,Sn-1=(n-1)2+(n-1),
所以当n≥2时,an=Sn-Sn-1=n2+n-[(n-1)2+(n-1)]=2n.
又a1=2=2×1,所以an=2n.
(2)当n=1时,,有成立;
当n≥2时,,
所以
,
又因为时,单调递增.
所以对一切正整数n,有.
7.(Ⅰ)在中,由余弦定理得:,
即,解得:,或(舍),
………………3分
由正弦定理得:
………………6分
(Ⅱ)由(Ⅰ)有:,,
所以,
………………9分
由正弦定理得:……………12分
在处取得最大值
,AD=2
由正弦定理得
10解:(I)∵、为的内角,
由知,结合正弦定理可得:
------------------------------------------------------------3分
,-----------------------------------------------------------------4分
∵
∴.--------------------------------------------------------5分
(II)解法1:∵,,
由余弦定理得:,----------------------------------------7分
整理得:
解得:或(不合舍去)--------------------------9分
∴,由得
的面积.--------------------------------------12分
【解法2:由结合正弦定理得:,---------------------6分
∵,
∴,
∴,-----------------------------7分
∴
=----------------------------9分
由正弦定理得:,-------------------------------------------------10分
∴的面积.------------------------------------12分】
11解:⑴设“当罚金定为10元时,闯红灯的市民改正行为”为事件,……2分
则………………………4分
∴当罚金定为10元时,比不制定处罚,行人闯红灯的概率会降低.……………6分
⑵由题可知类市民和类市民各有40人,故分别从类市民和类市民各抽出两人,设从类市民抽出的两人分别为、,设从类市民抽出的两人分别为、.
设从“类与类市民按分层抽样的方法抽取4人依次进行深度问卷”为事件,
………………………8分
则事件中首先抽出的事件有:,
,
,,共6种.
同理首先抽出、、的事件也各有6种.
故事件共有种.………………………10分
设从“抽取4人中前两位均为类市民”为事件,则事件有,
,,.
∴抽取4人中前两位均为类市民的概率是.………………………12分
12解(Ⅰ)分数在[70,80)内的频率为1-(0.010+0.015+0.015+0.025+0.005)×10=0.3,…2分
(Ⅱ)由频率频率分布直方图知前三组的频率之和为0.1+0.15+0.15=0.4,…………………3分
∴中位数在第四组,设中位数为70+x,则0.4+0.030×x=0.5 x=…………………4分
∴数据的中位数为70+=…………………5分
(Ⅲ)第1组有60×0.1=6人(设为1,2,3,4,5,6)
第6组有60×0.05=3人(设为A,B,C)…………………7分
从9人中任取2人有
共36种方法;…………………9分
其中抽取2人成绩之差的绝对值大于10的抽法是从第1组与第6组各抽取1人,抽法有
共18种,…………………11分
∴抽取2人成绩之差的绝对值大于10的概率为…………………12分
13解:(Ⅰ)
不满意
满意
合计
男
3
4
7
女
11
2
13
合计
14
6
20
-----------------------------2分
∵<3.84
1,
∴在犯错的概率不超过5%的前提下,不能认为“满意与否”与“性别”有关。-----------4分
(Ⅱ)因样本20人中,对该公司产品满意的有6人,故估计用户对该公司的产品“满意”的概率为,------------------------------------------------------------------6分
(Ⅲ)由(Ⅰ)知,对该公司产品满意的用户有6人,其中男用户4人,女用户2人,
设男用户分别为;女用户分别为,--------------------------------------8分
从中任选两人,记事件A为“选取的两个人都是男用户或都是女用户”,则
总的基本事件为
共15个,----------------------------------10分
而事件A包含的基本事件为共7个,
故.----------------------------------------------------------------12分
14解:(Ⅰ)由频率分布直方图可知,女生的频率为.
………1分
所以样本中女生总人数为.
………2分
由频率分布直方图可知,女生的频率为
,
…………4分
所以女生的频数为.
结合统计表可知,男生的频数为.
………6分
又因为样本容量为,故样本中,男、女生的频率分别为与,
…………7分
据频率估计概率、样本估计总体的统计思想,可知年段名学生中,的男生约有名,女生约有名.………8分
(Ⅱ)依题意,样本中女生的值约为
.10分
根据样本估计总体的统计思想,全体女生.
…………11分
因为,所以年段女生整体具有显著学科学习倾向.
…………12分
15解:(1),…………2分
错误!未找到引用源。………………4分
…………………6分
…………………7分
关于的线性回归方程是…………………8分
(2)年利润
…………………10分
…………………11分
所以当时,年利润最大.…………………12分
16解:(Ⅰ)连结,交于,连.
在三棱柱中,四边形为平行四边形,则,又是中点,
∴,而平面,平面,∴平面.
………4分
(Ⅱ)设点到平面的距离是,则,而,故当三棱锥体积最大时,,即平面.
……………6分
由(Ⅰ)知:,所以到平面的距离与到平面的距离相等.
∵平面,平面,∴,
∵是等边三角形,是中点,∴,又,平面,平面,∴平面,∴,由计算得:,所以,…9分
设到平面的距离为,由得:,所以到平面的距离是
……………12分
17解:
取中点为,连结,………1分
∵分别为中点
∴∥∥,
∴四点共面,
………3分
且平面平面
又平面,且∥平面
∴∥
∵为的中点,
∴是的中点,
………5分
∴.
………6分
(2)因为三棱柱为直三棱柱,∴平面,
又,则平面
设,又三角形是等腰三角形,所以.
方法一:如图,将几何体补成三棱柱
∴几何体的体积为:
………9分
又直三棱柱体积为:
………11分
故剩余的几何体棱台的体积为:
∴较小部分的体积与较大部分体积之比为:.
………12分
方法二:(分割)
几何体的体积为:
又直三棱柱体积为:
………11分
故剩余的几何体棱台的体积为:
∴较小部分的体积与较大部分体积之比为:.
………12分
18证明:(Ⅰ)∵,为线段的中点,
∴,,------------------------------------1分
故在四棱锥中,
又∵,且、为相交直线,
∴平面,---------------------------------------3分
又平面,∴平面平面;-------------5分
(Ⅱ)设,则,,
在等腰直角中,,;--------6分
由(Ⅰ)知是四棱锥的高,
故,
整理得,∴,--------------------------8分
连结,在中,由余弦定理可求得,
于是,
∵
为等腰三角形,其面积;------10分
设点F到平面的距离为,因,
由
所以点F到平面的距离为-------------------12分
19解:(1)连接,,,交于点,
∵底面是正方形,∴且为的中点.……2分
又∵,,∴平面.……4分
由于平面,故.
又∵,故;………………5分
(2)设的中点为,连接,,则,
∴为平行四边形,.………………(7分)
∵平面,∴平面,∴.
∵的中点为,∴.
由平面,可得,………………(9分)
又∵,,∴平面,∴.………………(10分)
又∵,∴平面,
∴,
故三棱锥的体积为.………………(12分)
20解析:(Ⅰ)证明:取的中点,连接,,.
,,………………………………………….
2分
又,.
为等边三角形.
,………….…….3分
又因为平面,平面,
.
平面.………………………………………..………….5分
又平面,因此;…………………………….6分
(Ⅱ)解:在等边中,在等边中;
在中.
是直角三角形,且,故.……….….8分
由(Ⅰ)得
又平面,平面,,
平面.
故是三棱锥的高.……………………………..…………….9分
又.
……………….12分
21解:(1)圆M的圆心为,则
,,故
椭圆C的方程为
(2)设,,由直线与椭圆C交于两点A,B
则
得
所以,
点M到直线的距离,则
显然,若点H也在线段AB上,则由对称性可知,直线就是y轴,矛盾
,
即,
解得,即
22解:(1)由圆的方程知圆的半径,因为直线互相垂直,且和圆相切,所以,即
①
又点在椭圆上,所以
②
联立①②,解得,
所以,所求圆的方程为
.
(2)因为直线和都与圆相切,所以,,
化简得,
因为点在椭圆上,所以,即,
所以.
23解:(Ⅰ)设圆A的半径为R,则
圆A的方程为
(II)当直线与x轴垂直时,易知符合题意;
当直线与x轴不垂直时,设直线的方程为,
连接,则
∵,∴
由,得,∴直线的方程为
(III)∵,∴=
当直线与x轴垂直时,得∴
当直线的斜率存在时,由,解得
∴
∴,∴是定值-5.
24解:(I)抛物线的准线方程为:,
,又,即……………2分
抛物线的方程为.
……………4分
(II)设,已知切线不为轴,设
联立,消去,可得
直线与抛物线相切,,即
代入,,即
……………………6分
设切点,则由几何性质可以判断点关于直线对称,则
,解得:,即……………………8分
直线的斜率为,
直线的斜率为,
,即三点共线.
……………………………………10分
当时,,此时共线.
综上:三点共线.
……………………………………12分
25解:(1)当,时,,
……………………………1分则
……………………………2分
令,解得,,
当或时,有;
当时,有,…………
5分
所以的单调递增区间和,的单调递减区间.
……………………………7分
(2)当,且
时,,.
则,
令,得或.
…………………8分
①当,即时,
此时当时,有,所以在上为减函数,
当时,有,所以在上为增函数,
………9分
又,,
所以的最大值为;
…………………………10分
②当,即时,
此时当时,;当时,;当时,;所以在上为增函数,在上为减函数,在上为增函数.
……………………12分
,
,
所以的最大值为,
…………………13分
综上,在区间上的最大值为
.
…………………14分
26解:(Ⅰ)设曲线与轴相切于点,则,,即,解得.
因此,当时,轴是曲线的切线.
(II)解法1:,整理得
∵,,且等号不能成立,∴
∴等价于恒成立,令
,其中,∴
又因为,所以
∴函数在区间上单调递增,,
∴
解法2.
,整理得
即,令
①当,即时,,故在区间上单调递增,
,∴
②当,即时,,故在区间上单调递减,
,∴解得,
∴此种情况不符合题意
③当时,,
其中,,,∴,∴此种情况不符合题意
综上,
27解:⑴,
…………2分
,即:
.
………
4分
⑵令,
对恒成立
在内单调递增,且
………6分
①当,即时,
在上为增函数
………8分
②当,即时,
由在内单调递增知:
存在唯一,使得,即.
令,得,,得;
………
10分
,即.
由①易知函数单减,故
综上,实数的取值范围是.
………
12分
28解:(1)由题意......................1分
当时,函数在上是减函数,
当时,此时函数在上是减函数,在上是增函数,
当时,函数在上是增函数..................................4分
(2)设切点,
∴切线的斜率.......................................5分
即:,
即:,
所以过点有且仅有一条直线与函数的图象相切等价于方程
在定义域上有且只有一个解;................6分
令,则在上有且只有一个零点;
设.......................7分
①当时,在单减,在单增,最小值,在上恒正,在上恒正,不符合条件;
②当时,,在为增函数,,
此时在上恒正,不符合条件;
③当时,在为增函数,,此时在上恒正,不符合条件;
④当时,在为增函数,,
当
当,即:时,
上恰有一个零点;不符合条件;
综上:.............................................12分
选做题参考答案:
1解:(1)由,得,即曲线的直角坐标方程为.
(2)方法一:
将直线的方程代入,并整理得,,.
所以.
方法二:弦长公式
直线的普通方程;
设直线交曲线于,则
,消去得,,,;
所以,直线被曲线截得的线段的长为.
2解:(1)把代入ρsin2θ=2acos
θ,得y2=2ax(a>0),
(t为参数),消去t得x-y-2=0,
∴曲线C的直角坐标方程和直线l的普通方程分别是y2=2ax(a>0),x-y-2=0.
(2)将(t为参数)代入y2=2ax,整理得t2-2(4+a)t+8(4+a)=0.
设t1,t2是该方程的两根,则t1+t2=2(4+a),t1·t2=8(4+a),
∵|MN|2=|PM|·|PN|,∴(t1-t2)2=(t1+t2)2-4t1·t2=t1·t2,
∴8(4+a)2-4×8(4+a)=8(4+a),
∴a=1.
3解:(1)圆的参数方程为(为参数)
所以普通方程为
圆的极坐标方程:
(2)点到直线:的距离为
△的面积
所以△面积的最大值为。
4解:(1),
所以为圆心是,半径是1的圆.
为中心是坐标原点,焦点在轴上,长半轴长是8,短半轴长是3的椭圆.
(2)
当时,,
设,则,
为直线,
到的距离
(其中),所以,d的最小值是
5解:(1)曲线C的直角坐标方程为
即
曲线C为圆心为(3,0),半径为2的圆.
直线l的方程为:
∵直线l与曲线C相切
∴
,即
∵
[0,π)
∴ =
(2)设,
则,
的取值范围是.
6解:(1)圆的普通方程是,又;
所以圆的极坐标方程是.
(2)设为点的极坐标,则有
,
解得.
设为点的极坐标,则有
解得
由于,所以,所以线段的长为2.
3
3
4
6
8
5
1
3
6
4
6
2
4
5
5
1
7
3
3
5
6
9
8
3
2
1
图3
A
B
C
D
(第19题图)
第19题图
A
C
D
B
(第17题图)
O
D
同课章节目录
