2016-2017学年深圳大浪实验学校九年级下第3章《圆》测试卷(无答案)
文档属性
| 名称 | 2016-2017学年深圳大浪实验学校九年级下第3章《圆》测试卷(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 345.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-04 00:00:00 | ||
图片预览


文档简介
深圳市龙华区大浪实验学校九年级数学单元测试卷
《圆》
一、单项选择题(3×12=36分)
1、三角形的外心是(
)
A.三角形三条中线的交点
B.三角形三边垂直平分线的交点
C.三角形三条内角平分线的交点
D.三角形三条高的交点
2、如图,⊙O的直径AB=6,点C在⊙O上,∠ABC=30°,则AC的长是(
)
A.3
B.4
C.
D.
3、如图,
AB为⊙O的直径,CD为弦,AB⊥CD
,如果∠BOC
=
70
,
那么∠A的度数为(
)
A.70°
B.35°
C.30°
D.20°
4、已知两圆的直径分别是2厘米与4厘米,圆心距是3厘米,则这两个圆的位置关系是(
)
A.相交
B.外切
C.外离
D.内含
5、如图,AB是⊙O的直径,点C、D在⊙O上,OD//AC,下列结论错误的是(
)
A.∠BOD=∠BAC
B.∠BOD=∠COD
C.∠BAD=∠CAD
D.∠C=∠D
6、能在同一个圆上的是(
)
A.平行四边形的四个顶点
B.梯形的四个顶点
C.矩形的四个顶点
D.菱形的四个顶点
7、如图,直线与两个同心圆分别交于图示的各点,则正确的是(
)
A.MP=RN
B.MPC.MP>RN
D.MP与RN的大小关系不定
8、⊙O的半径为5,弦AB的长为8,M是弦AB
上的动点,则线段OM长的最小值为(
)
A.5
B.4
C.3
D.2
9、如图,在5×5的正方形网格中,一条圆弧经过点A、B、C三点,
那么这条圆弧所在圆的圆心是(
)
A.点P
B.点Q
C.点R
D.点M[]
10、在圆柱形油槽内装有一些油,截面如图,油面宽AB为6分米,如果再注入一些油后,油面AB上升1分米,油面宽变为8分米,油槽直径为(
)分米.
A.12
B.10
C.8
D.6
11、已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D,则∠CDP等于(
)
A.30°
B.60°
[]
C.45°
D.50°
12、如图,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2.则BD的长为(
)
A.
B.
C.
D.
二、填空题(3×4=12分)
13、已知⊙O1与⊙O2相切,若⊙O1的半径为1,两圆的圆心距为5,则⊙O2的半径为
▲
.
14、给出下列说法:①三点确定一个圆;②三角形有且只有一个外接圆;③圆有且只有一个外切三角形;④三角形的内心是三边中线的交点;⑤直角三角形的外心一定在斜边中点.
其中正确命题的序号是
▲
.[]
15、如图,量角器外缘边上有A、P、B三点,点A和点B在量角器的外圈的读数分别为100°和160°,则∠APB的大小为
▲
.
16、半径为5的圆中,弦AB//CD,AB=6cm,CD=8cm,则弦AB与CD之间的距离为
▲
.
姓名:
班级:
得分:
选择题
1[]
2
3
4
5
6
7
8
9
10
11
12
答
案
填空题
13
14
15
16
答
案
三、解答题(52分)
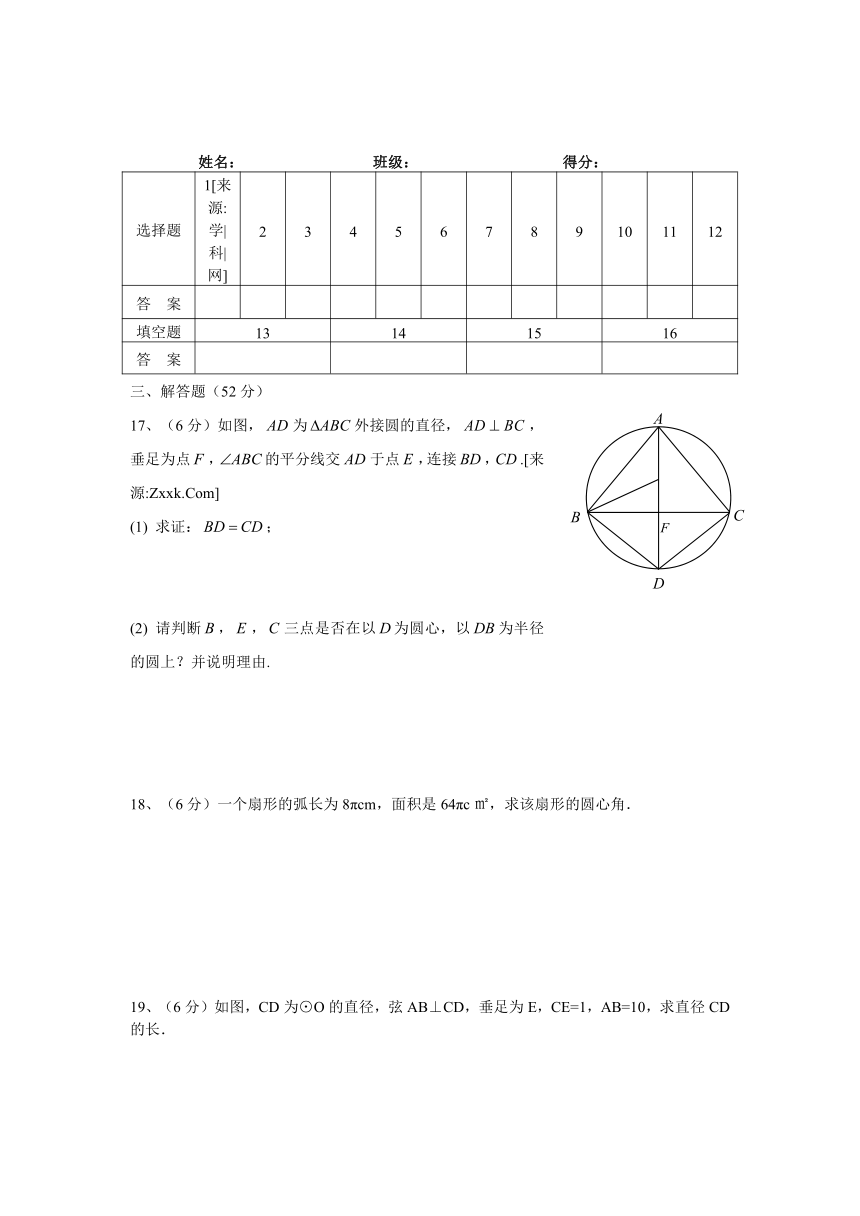
17、(6分)如图,为外接圆的直径,,垂足为点,的平分线交于点,连接,.[]
(1)
求证:;
(2)
请判断,,三点是否在以为圆心,以为半径的圆上?并说明理由.
18、(6分)一个扇形的弧长为8πcm,面积是64πc㎡,求该扇形的圆心角.
19、(6分)如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1,AB=10,求直径CD的长.
20、(7分)如图,平面直角坐标系中,M是双曲线上的一点,⊙M与y轴切于点C,与x轴交于A、B两点。若点C的坐标为(0,2),点A的坐标为(1,0),求k的值.
21、(8分)如图,C是以AB为直径的⊙O上一点,过O作AC的垂线交切线AF于F,OF交AC于点E,连接CF并延长交BA延长线于P.
(1)求证:PC是⊙O的切线.
(2)若PA=4,PF=5,求⊙O的半径长.
22、(9分)如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
(1)求证:△ABE∽△ADB;
(2)求tanC;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
23、(10分)如图,直线交x轴于A、交y轴于B,P(m,n)为函数(x>0)的图象上一点.PC⊥x轴于C,交直线AB于D;PE⊥y轴于E,交直线AB于F.
(1)直接写出点D、F的坐标(用含m、n的式子表示);
(2)当直线AB与线段PC、PE都相交时,过D、P、F三点的圆与线段OD交于点G,连接FG.证明以F为圆心、FG为半径的⊙F与OD相切;
(3)证明△ODF∽△BDO.
x
y
B
A
M
O
C
y
x
O
A
C
P
E
B
F
D
G
《圆》
一、单项选择题(3×12=36分)
1、三角形的外心是(
)
A.三角形三条中线的交点
B.三角形三边垂直平分线的交点
C.三角形三条内角平分线的交点
D.三角形三条高的交点
2、如图,⊙O的直径AB=6,点C在⊙O上,∠ABC=30°,则AC的长是(
)
A.3
B.4
C.
D.
3、如图,
AB为⊙O的直径,CD为弦,AB⊥CD
,如果∠BOC
=
70
,
那么∠A的度数为(
)
A.70°
B.35°
C.30°
D.20°
4、已知两圆的直径分别是2厘米与4厘米,圆心距是3厘米,则这两个圆的位置关系是(
)
A.相交
B.外切
C.外离
D.内含
5、如图,AB是⊙O的直径,点C、D在⊙O上,OD//AC,下列结论错误的是(
)
A.∠BOD=∠BAC
B.∠BOD=∠COD
C.∠BAD=∠CAD
D.∠C=∠D
6、能在同一个圆上的是(
)
A.平行四边形的四个顶点
B.梯形的四个顶点
C.矩形的四个顶点
D.菱形的四个顶点
7、如图,直线与两个同心圆分别交于图示的各点,则正确的是(
)
A.MP=RN
B.MP
D.MP与RN的大小关系不定
8、⊙O的半径为5,弦AB的长为8,M是弦AB
上的动点,则线段OM长的最小值为(
)
A.5
B.4
C.3
D.2
9、如图,在5×5的正方形网格中,一条圆弧经过点A、B、C三点,
那么这条圆弧所在圆的圆心是(
)
A.点P
B.点Q
C.点R
D.点M[]
10、在圆柱形油槽内装有一些油,截面如图,油面宽AB为6分米,如果再注入一些油后,油面AB上升1分米,油面宽变为8分米,油槽直径为(
)分米.
A.12
B.10
C.8
D.6
11、已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D,则∠CDP等于(
)
A.30°
B.60°
[]
C.45°
D.50°
12、如图,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2.则BD的长为(
)
A.
B.
C.
D.
二、填空题(3×4=12分)
13、已知⊙O1与⊙O2相切,若⊙O1的半径为1,两圆的圆心距为5,则⊙O2的半径为
▲
.
14、给出下列说法:①三点确定一个圆;②三角形有且只有一个外接圆;③圆有且只有一个外切三角形;④三角形的内心是三边中线的交点;⑤直角三角形的外心一定在斜边中点.
其中正确命题的序号是
▲
.[]
15、如图,量角器外缘边上有A、P、B三点,点A和点B在量角器的外圈的读数分别为100°和160°,则∠APB的大小为
▲
.
16、半径为5的圆中,弦AB//CD,AB=6cm,CD=8cm,则弦AB与CD之间的距离为
▲
.
姓名:
班级:
得分:
选择题
1[]
2
3
4
5
6
7
8
9
10
11
12
答
案
填空题
13
14
15
16
答
案
三、解答题(52分)
17、(6分)如图,为外接圆的直径,,垂足为点,的平分线交于点,连接,.[]
(1)
求证:;
(2)
请判断,,三点是否在以为圆心,以为半径的圆上?并说明理由.
18、(6分)一个扇形的弧长为8πcm,面积是64πc㎡,求该扇形的圆心角.
19、(6分)如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1,AB=10,求直径CD的长.
20、(7分)如图,平面直角坐标系中,M是双曲线上的一点,⊙M与y轴切于点C,与x轴交于A、B两点。若点C的坐标为(0,2),点A的坐标为(1,0),求k的值.
21、(8分)如图,C是以AB为直径的⊙O上一点,过O作AC的垂线交切线AF于F,OF交AC于点E,连接CF并延长交BA延长线于P.
(1)求证:PC是⊙O的切线.
(2)若PA=4,PF=5,求⊙O的半径长.
22、(9分)如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
(1)求证:△ABE∽△ADB;
(2)求tanC;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
23、(10分)如图,直线交x轴于A、交y轴于B,P(m,n)为函数(x>0)的图象上一点.PC⊥x轴于C,交直线AB于D;PE⊥y轴于E,交直线AB于F.
(1)直接写出点D、F的坐标(用含m、n的式子表示);
(2)当直线AB与线段PC、PE都相交时,过D、P、F三点的圆与线段OD交于点G,连接FG.证明以F为圆心、FG为半径的⊙F与OD相切;
(3)证明△ODF∽△BDO.
x
y
B
A
M
O
C
y
x
O
A
C
P
E
B
F
D
G
