广东省深圳市2017届中考数学 第17课时《反比例函数》复习学案(无答案)
文档属性
| 名称 | 广东省深圳市2017届中考数学 第17课时《反比例函数》复习学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 204.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-04 00:00:00 | ||
图片预览

文档简介
函数与方程
反比例函数
【知识梳理】
知识点1:反比例函数的概念
如果
(
为常数,)
,那么是的反比例函数。
注意:反比例函数的解析式有三种常见的表达形式:
()
,
()
,()
知识点2:反比例函数的图象和性质:
反比例函数的图象是双曲线,双曲线无限的靠近坐标轴,但是与坐标轴永远不相交,反比例函数的图像既是轴对称图形,又是中心对称图形。
反比例函数的图象和性质:
函数
的符号
图像位置
增减性
>0
一、三象限
在每一象限内,随的增大减小
<0
二、四象限
在每一象限内,随的增大增大
知识点3:待定系数法
确定反比例函数解析式的方法仍是待定系数法。由于在反比例函数中,只有一个待定系数,因此只需要一对对应值或图像上的一个点的坐标,即可求出的值,从而确定其解析式。
知识点4:反比例函数的的几何意义
如下图,过反比例函数图像上任一点P作x轴、y轴的垂线PM,PN,则所得的矩形PMON的面积S=PMPN=。
。
【中考展示】
1.(2014深圳)如图1,双曲线经过Rt△BOC斜边上的点A,且满足,与BC交于点D,S△BOD=21,求k= .
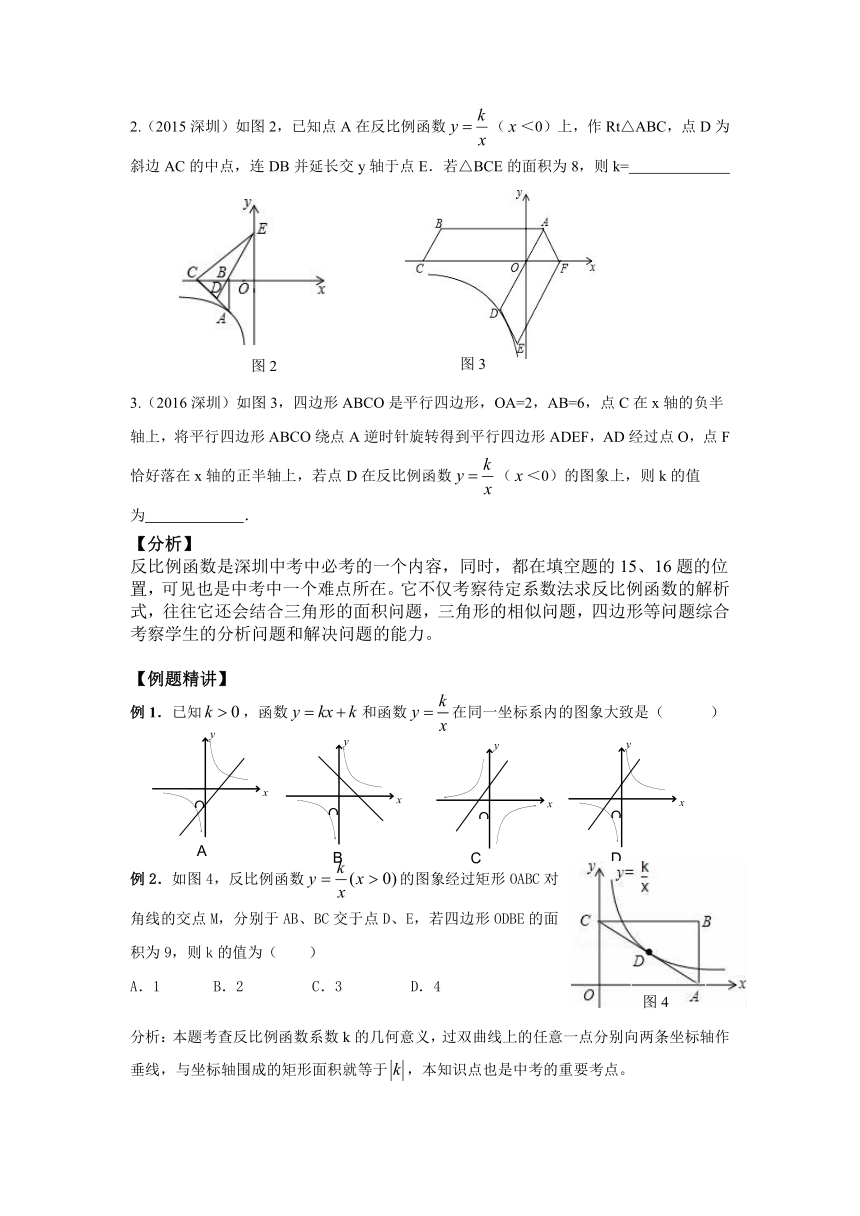
2.(2015深圳)如图2,已知点A在反比例函数(<0)上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E.若△BCE的面积为8,则k=
3.(2016深圳)如图3,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,点F恰好落在x轴的正半轴上,若点D在反比例函数(<0)的图象上,则k的值为
.
【分析】
反比例函数是深圳中考中必考的一个内容,同时,都在填空题的15、16题的位置,可见也是中考中一个难点所在。它不仅考察待定系数法求反比例函数的解析式,往往它还会结合三角形的面积问题,三角形的相似问题,四边形等问题综合考察学生的分析问题和解决问题的能力。
【例题精讲】
例1.已知,函数和函数在同一坐标系内的图象大致是(
)
例2.如图4,反比例函数的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
A.1
B.2
C.3
D.4
分析:本题考查反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于,本知识点也是中考的重要考点。
举一反三:如图5,点A,B在反比例函数的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 .
例3.工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图6).已知该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
分析:考查了反比例函数和一次函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
例4.如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,
(1)求反比例函数的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
分析:本题考查了反比例函数和一次函数以及三角函数的应用。
【课堂练习】
1、已知反比例函数的图象经过点A(1,﹣2),则k=
.
2、已知反比例函数的图像过点P(1,3),则反比例函数图像位于(
)
A.第一、二象限
B.第一、三象限
C.第二、四象限
D.第三、四象限
3、若反比例函数的图象上有两点和,那么(
).
A.
B.
C.
D.
4、如图8,过点C(1,2)分别作x轴、y轴的平行线,交直线y=﹣x+6于A、B两点,若反比例函数的图象与△ABC有公共点,则k的取值范围是( )
A. B. C. D.
5、如图,已知一次函数()的图象与反比例函数(>0)的图
象相交于A(1,2)、B(-2,-1)两点,且与轴相交于点C.连接OA、OB.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积;
(3)在x轴上求点E,使△ACE为直角三角形.(直接写出点E的坐标)
(4)若点Q为反比例函数(>0)图象上的动点,在轴的正半轴上是否存在一点P,使得以P、Q、O为顶点的三角形与△AOC相似?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
图1
图3
图2
O
O
O
O
D
B
A
C
图4
图5
图6
图7
图8
反比例函数
【知识梳理】
知识点1:反比例函数的概念
如果
(
为常数,)
,那么是的反比例函数。
注意:反比例函数的解析式有三种常见的表达形式:
()
,
()
,()
知识点2:反比例函数的图象和性质:
反比例函数的图象是双曲线,双曲线无限的靠近坐标轴,但是与坐标轴永远不相交,反比例函数的图像既是轴对称图形,又是中心对称图形。
反比例函数的图象和性质:
函数
的符号
图像位置
增减性
>0
一、三象限
在每一象限内,随的增大减小
<0
二、四象限
在每一象限内,随的增大增大
知识点3:待定系数法
确定反比例函数解析式的方法仍是待定系数法。由于在反比例函数中,只有一个待定系数,因此只需要一对对应值或图像上的一个点的坐标,即可求出的值,从而确定其解析式。
知识点4:反比例函数的的几何意义
如下图,过反比例函数图像上任一点P作x轴、y轴的垂线PM,PN,则所得的矩形PMON的面积S=PMPN=。
。
【中考展示】
1.(2014深圳)如图1,双曲线经过Rt△BOC斜边上的点A,且满足,与BC交于点D,S△BOD=21,求k= .
2.(2015深圳)如图2,已知点A在反比例函数(<0)上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E.若△BCE的面积为8,则k=
3.(2016深圳)如图3,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,点F恰好落在x轴的正半轴上,若点D在反比例函数(<0)的图象上,则k的值为
.
【分析】
反比例函数是深圳中考中必考的一个内容,同时,都在填空题的15、16题的位置,可见也是中考中一个难点所在。它不仅考察待定系数法求反比例函数的解析式,往往它还会结合三角形的面积问题,三角形的相似问题,四边形等问题综合考察学生的分析问题和解决问题的能力。
【例题精讲】
例1.已知,函数和函数在同一坐标系内的图象大致是(
)
例2.如图4,反比例函数的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
A.1
B.2
C.3
D.4
分析:本题考查反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于,本知识点也是中考的重要考点。
举一反三:如图5,点A,B在反比例函数的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 .
例3.工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图6).已知该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
分析:考查了反比例函数和一次函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
例4.如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,
(1)求反比例函数的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
分析:本题考查了反比例函数和一次函数以及三角函数的应用。
【课堂练习】
1、已知反比例函数的图象经过点A(1,﹣2),则k=
.
2、已知反比例函数的图像过点P(1,3),则反比例函数图像位于(
)
A.第一、二象限
B.第一、三象限
C.第二、四象限
D.第三、四象限
3、若反比例函数的图象上有两点和,那么(
).
A.
B.
C.
D.
4、如图8,过点C(1,2)分别作x轴、y轴的平行线,交直线y=﹣x+6于A、B两点,若反比例函数的图象与△ABC有公共点,则k的取值范围是( )
A. B. C. D.
5、如图,已知一次函数()的图象与反比例函数(>0)的图
象相交于A(1,2)、B(-2,-1)两点,且与轴相交于点C.连接OA、OB.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积;
(3)在x轴上求点E,使△ACE为直角三角形.(直接写出点E的坐标)
(4)若点Q为反比例函数(>0)图象上的动点,在轴的正半轴上是否存在一点P,使得以P、Q、O为顶点的三角形与△AOC相似?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
图1
图3
图2
O
O
O
O
D
B
A
C
图4
图5
图6
图7
图8
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
