八年级上学期巧用函数图象破解不等式问题 学案
文档属性
| 名称 | 八年级上学期巧用函数图象破解不等式问题 学案 |  | |
| 格式 | zip | ||
| 文件大小 | 271.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-03 16:46:56 | ||
图片预览

文档简介
巧用函数图象破解不等式问题
求解不等式问题往往需要一定的技巧.这里介绍利用图象法求不等式(组)的解集,可以迅速准确巧妙地求解不等式问题.
一、知识储备
以一次函数为例.
一个函数值的正负
设一次函数为,其图象与轴交于.
(1)若,如图1.
当时,函数图象对应的部分在轴下方,所以函数值,因此不等式的解集是;
当时,函数图象对应的部分在轴上方,所以函数值,因此不等式的解集是.
(2)若,如图2.
当时,函数图象对应的部分在轴上方,所以函数值,因此不等式的解集是;
当时,函数图象对应的部分在轴下方,所以函数值,因此不等式的解集是.
2.比较两个函数值的大小
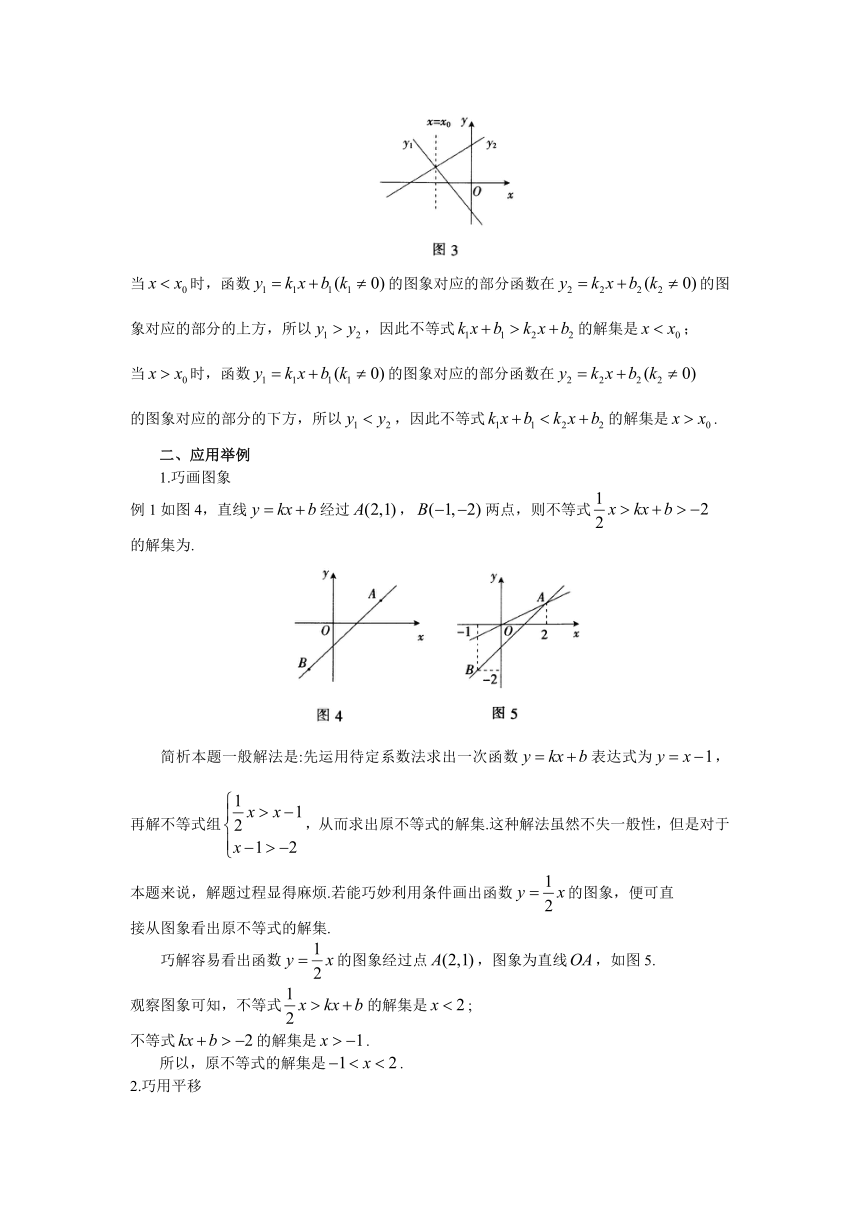
如图3,设两个一次函数分别为,,两个函数图象交于.
当时,函数的图象对应的部分函数在的图象对应的部分的上方,所以,因此不等式的解集是;
当时,函数的图象对应的部分函数在
的图象对应的部分的下方,所以,因此不等式的解集是.
二、应用举例
1.巧画图象
例1如图4,直线经过,两点,则不等式
的解集为.
简析本题一般解法是:先运用待定系数法求出一次函数表达式为,再解不等式组,从而求出原不等式的解集.这种解法虽然不失一般性,但是对于本题来说,解题过程显得麻烦.若能巧妙利用条件画出函数的图象,便可直
接从图象看出原不等式的解集.
巧解容易看出函数的图象经过点,图象为直线,如图5.
观察图象可知,不等式的解集是;
不等式的解集是.
所以,原不等式的解集是.
2.巧用平移
例2若函数的图象如图6所示,则关于的不等式的解集
是.
简析本题很难用常规思维求解.事实上,如果根据图象可以判断出,不等式两边都除以时,不等号必须改变方向,应该得,所以.又因为经过点,代入后又得,所以原不等式的解集是.这个解法不仅麻烦,更容易出错.
若能看出不等式左端的代数式对应的函数图象可以通过直线平移获得,即
可巧解.
巧解把直线向右平移个单位,得到直线,并且它与轴交于(如图7).观察可见原不等式的解集是.
3.巧用与轴交点坐标
例3如图8,直线与的交点的横坐标为,则关于的不等式的解集为.
简析本题的易错点在于求不等式解集时,两边除以,得,已错也.学生解含有字母系数的不等式总不设防,容易犯错.而变换一下策略就能避开陷阱.
因为不等式表示函数的值大于,所以只需求出函数的图象与轴交点的横坐标,即可利用图象得出不等式的解集.
巧解令,解得,如图9.
观察图象,可得不等式的解集是
;
又不等式的解集是
.
所以,原不等式的解集是.
4.巧变形,再用图
例4一次函数与正比例函数的图象如图10所示,则不等式的解集是.
简析本题一般解法是,先求出一次函数与正比例函数的图象的交点坐标,再把和分别代入,得
,解得
然后代入原不等式求出解集,甚是麻烦.若将原不等式适当变形,利用图象求解集,则非常简单.
巧解将不等式变形为,此不等式表示一次函数的值小于正比例函数的值.
观察图象,可知的取值范围是,即为原不等式的解集.
例5一次函数与反比例函数的在同一坐标系内的图象如图11所示,则不等式的解集是.
简析本题一般解法是:把和分别代入一次函数表达式,可求得,.把代入,得,把代入反比例函数表达式,得,所以,原不等式是,即,它表示一次函数的值大于或等于反比例函数的值,令,解得,,利用图象可得不等式的解集是或,即为原不等式的解集.
巧解把不等式变形为,它表示一次函数的值大于或等于反比例函数的值.而一次函数的图象可由的图象向右平移个单位长度得到,并且一次函数的图象与的图象恰好关于原点对称,如图12.我们知道,反比例函数图象也关于原点对称,因此一次函数的图象与反比例函数的图象的交点,和一次函数的图象与反比例函数上的图象的交点,分别关于原点对称.根据对称性,可知点,的横坐标分别是和,所以原不等式的解集是或.
从以上数例可以看出,用图象法求不等式的解集,重在观察图象,巧在充分利用和发掘题目自身的隐含条件,化隐为显,把问题转化为基本模型,即可顺利解决,大大提高了求解不等式问题的效率.
求解不等式问题往往需要一定的技巧.这里介绍利用图象法求不等式(组)的解集,可以迅速准确巧妙地求解不等式问题.
一、知识储备
以一次函数为例.
一个函数值的正负
设一次函数为,其图象与轴交于.
(1)若,如图1.
当时,函数图象对应的部分在轴下方,所以函数值,因此不等式的解集是;
当时,函数图象对应的部分在轴上方,所以函数值,因此不等式的解集是.
(2)若,如图2.
当时,函数图象对应的部分在轴上方,所以函数值,因此不等式的解集是;
当时,函数图象对应的部分在轴下方,所以函数值,因此不等式的解集是.
2.比较两个函数值的大小
如图3,设两个一次函数分别为,,两个函数图象交于.
当时,函数的图象对应的部分函数在的图象对应的部分的上方,所以,因此不等式的解集是;
当时,函数的图象对应的部分函数在
的图象对应的部分的下方,所以,因此不等式的解集是.
二、应用举例
1.巧画图象
例1如图4,直线经过,两点,则不等式
的解集为.
简析本题一般解法是:先运用待定系数法求出一次函数表达式为,再解不等式组,从而求出原不等式的解集.这种解法虽然不失一般性,但是对于本题来说,解题过程显得麻烦.若能巧妙利用条件画出函数的图象,便可直
接从图象看出原不等式的解集.
巧解容易看出函数的图象经过点,图象为直线,如图5.
观察图象可知,不等式的解集是;
不等式的解集是.
所以,原不等式的解集是.
2.巧用平移
例2若函数的图象如图6所示,则关于的不等式的解集
是.
简析本题很难用常规思维求解.事实上,如果根据图象可以判断出,不等式两边都除以时,不等号必须改变方向,应该得,所以.又因为经过点,代入后又得,所以原不等式的解集是.这个解法不仅麻烦,更容易出错.
若能看出不等式左端的代数式对应的函数图象可以通过直线平移获得,即
可巧解.
巧解把直线向右平移个单位,得到直线,并且它与轴交于(如图7).观察可见原不等式的解集是.
3.巧用与轴交点坐标
例3如图8,直线与的交点的横坐标为,则关于的不等式的解集为.
简析本题的易错点在于求不等式解集时,两边除以,得,已错也.学生解含有字母系数的不等式总不设防,容易犯错.而变换一下策略就能避开陷阱.
因为不等式表示函数的值大于,所以只需求出函数的图象与轴交点的横坐标,即可利用图象得出不等式的解集.
巧解令,解得,如图9.
观察图象,可得不等式的解集是
;
又不等式的解集是
.
所以,原不等式的解集是.
4.巧变形,再用图
例4一次函数与正比例函数的图象如图10所示,则不等式的解集是.
简析本题一般解法是,先求出一次函数与正比例函数的图象的交点坐标,再把和分别代入,得
,解得
然后代入原不等式求出解集,甚是麻烦.若将原不等式适当变形,利用图象求解集,则非常简单.
巧解将不等式变形为,此不等式表示一次函数的值小于正比例函数的值.
观察图象,可知的取值范围是,即为原不等式的解集.
例5一次函数与反比例函数的在同一坐标系内的图象如图11所示,则不等式的解集是.
简析本题一般解法是:把和分别代入一次函数表达式,可求得,.把代入,得,把代入反比例函数表达式,得,所以,原不等式是,即,它表示一次函数的值大于或等于反比例函数的值,令,解得,,利用图象可得不等式的解集是或,即为原不等式的解集.
巧解把不等式变形为,它表示一次函数的值大于或等于反比例函数的值.而一次函数的图象可由的图象向右平移个单位长度得到,并且一次函数的图象与的图象恰好关于原点对称,如图12.我们知道,反比例函数图象也关于原点对称,因此一次函数的图象与反比例函数的图象的交点,和一次函数的图象与反比例函数上的图象的交点,分别关于原点对称.根据对称性,可知点,的横坐标分别是和,所以原不等式的解集是或.
从以上数例可以看出,用图象法求不等式的解集,重在观察图象,巧在充分利用和发掘题目自身的隐含条件,化隐为显,把问题转化为基本模型,即可顺利解决,大大提高了求解不等式问题的效率.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
