八年级上册例析共高三角形的应用 学案

例析共高三角形的应用
具有公共高的两个三角形，可称之为共高三角形.共高三角形有下面的一个简单而有用的性质.
如图1，点在的边上，由三角形的面积公式，得
即共高三角形的面积比等于底之比.
利用这一性质解题，能提高解题效率.下面举例说明.
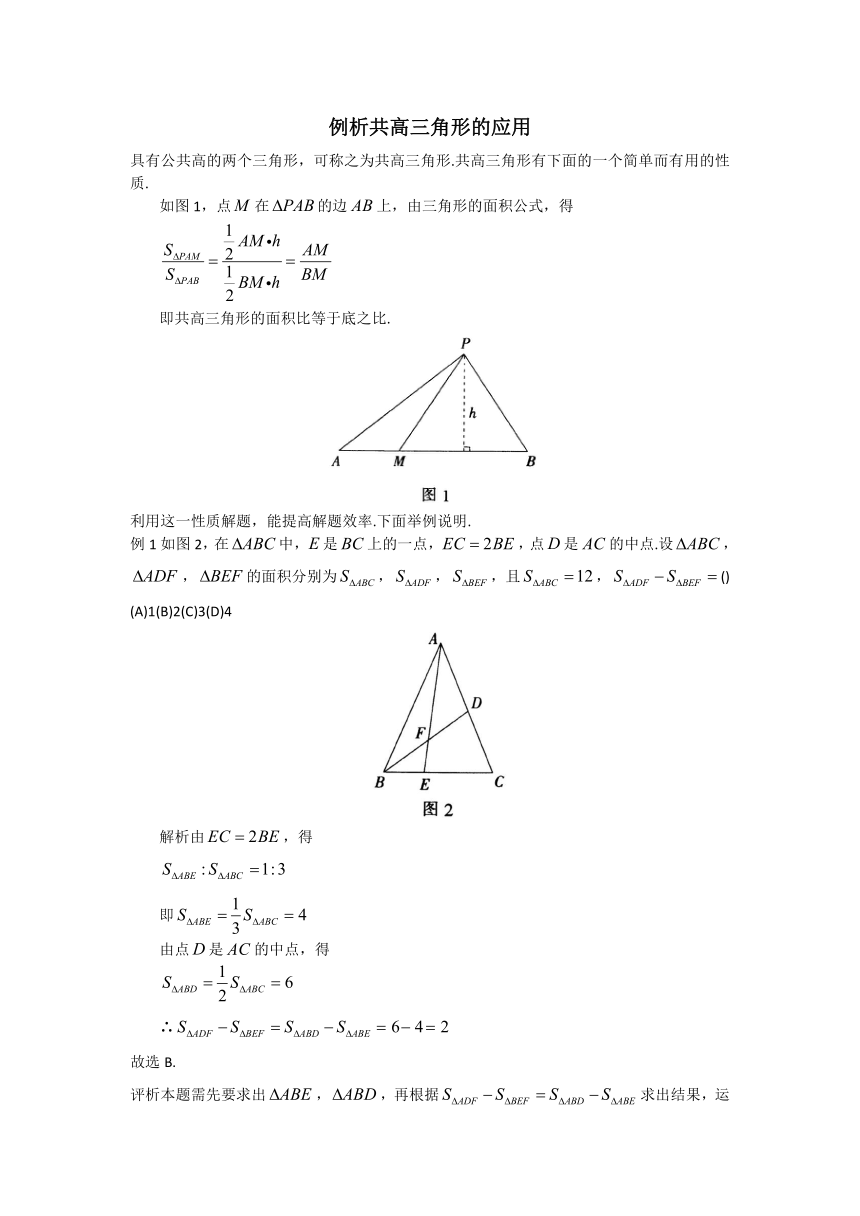
例1如图2，在中，是上的一点，，点是的中点.设，，的面积分别为，，，且，()
(A)1(B)2(C)3(D)4
解析由，得
即
由点是的中点，得
∴
故选B.
评析本题需先要求出，，再根据求出结果，运用了转化思想.
例2如图3，在中，点、、分别是、、上的中点，且的面积为cm2，则的面积为cm2.
解析连结，由是的中点，得
由是的中点，得
，
∴
由是的中点，得
故填3.
评析本题多次利用共高三角形面积的性质获得结果.可见，在解决面积相关问题时，若遇到中点，定有两个面积相等的三角形，这也启发我们可利用中点构造新的三角形.本例中，利用线段的中点，连结，构造是解题的关键.
例3如图4，、分别是的边、边上的点，线段、交于点，已知，，的面积分别为，，.求的面积.
解析由，
可得
即，解得
由，
可得
即
∴
解得.
评析本题先根据与为底三角形面积关系求得面积，然后根据与为底三角形面积关系求得的面积.这里也可以利用与为底三角形关系来求的面积.
例4如图5，在中，，，，的面积为cm2，求的面积.
解析由，得
①
连接，由，得
②
②，得
同理得，
∴
即
代入得
解得.
评析根据题中线段比值关系，可以找到等高的三角形面积关系.在本例中，关键要找到，，与待求的面积关系，这需要构造新的三角形才能实现，为此要连结，，，继而获解.