九年级数学上册利用几何模型解一道竞赛题 学案
文档属性
| 名称 | 九年级数学上册利用几何模型解一道竞赛题 学案 |  | |
| 格式 | zip | ||
| 文件大小 | 194.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-03 16:49:24 | ||
图片预览

文档简介
利用几何模型解一道竞赛题
本文借助一道2017年的全国数学竞赛题,展示五种几何模型的应用.
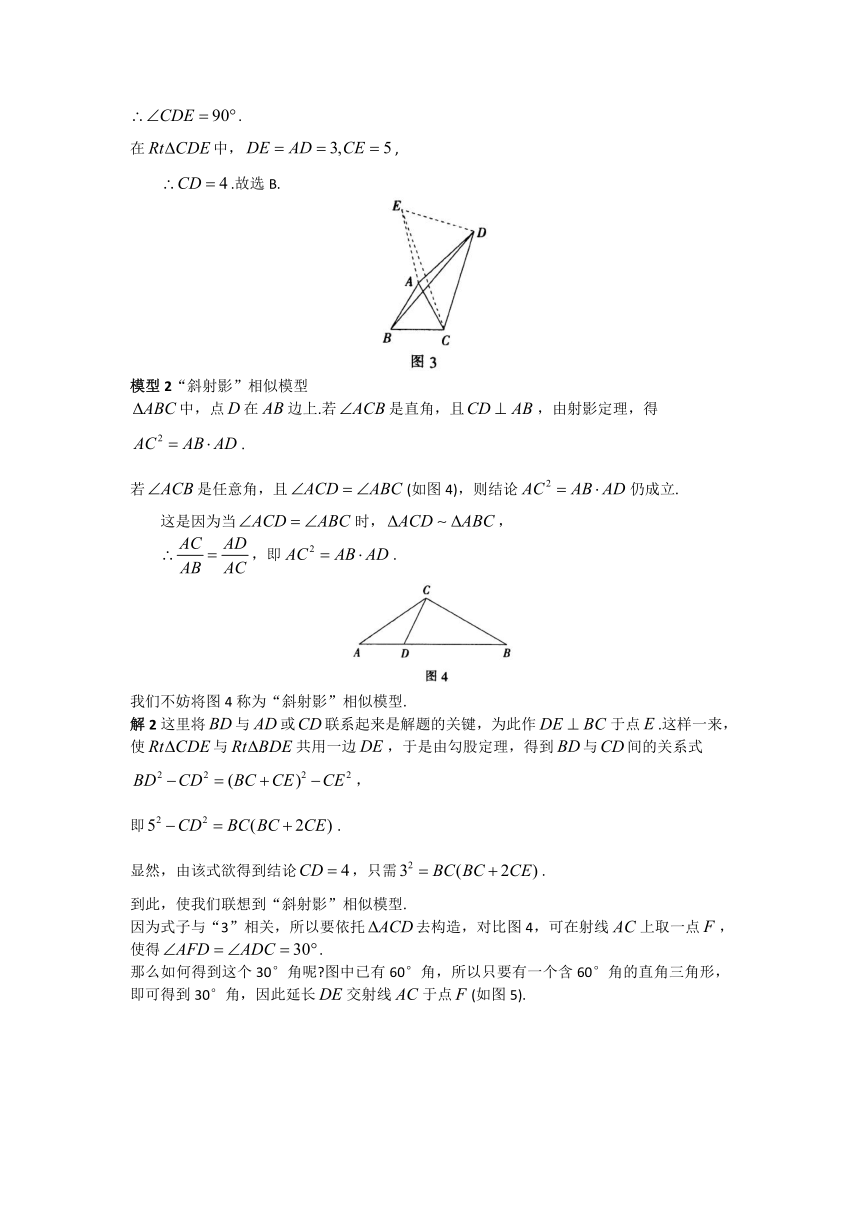
题目如图1,四边形中,是对角线,是等边三角形,,则的长为()
(A)
(B)4
(C)
(D)4.5
模型1“手拉手”全等模型
如图2,与都是等腰三角形,顶角分别为与,且,则.
下面就图2的(1)与(3)说明结论成立.
由题意,知,
又
(如图2(1)),
或
(如图2(3)),
.
解1因为是等边三角形,所以只需以(或以)为边作一个等边三角形,便构造出“手拉手”全等模型.
现以为边作等边(如图3),连结,则
.
,
.
在中,,
.故选B.
模型2“斜射影”相似模型
中,点在边上.若是直角,且,由射影定理,得
.
若是任意角,且(如图4),则结论仍成立.
这是因为当时,,
,即.
我们不妨将图4称为“斜射影”相似模型.
解2这里将与或联系起来是解题的关键,为此作于点.这样一来,使与共用一边,于是由勾股定理,得到与间的关系式
,
即.
显然,由该式欲得到结论,只需.
到此,使我们联想到“斜射影”相似模型.
因为式子与“3”相关,所以要依托去构造,对比图4,可在射线上取一点,使得.
那么如何得到这个30°角呢 图中已有60°角,所以只要有一个含60°角的直角三角形,即可得到30°角,因此延长交射线于点(如图5).
,
.
由“斜射影”相似模型,得
.
显然,,
.
据以上分析,得,故选B.
模型3“一线三等角”相似模型
如图6,直线上有三点,点在直线同侧,若
,则.
简证
.
又.
特别地,当与有一组对应边相等时,有.
解3因为,所以若在线段上取一点,使,则.故,从而,所以原问题转化为求的长.
另一方面,因为的顶点在直线上,且,所以若作的外接等边,则构造出三组“一线三等角”形,而且构造出的含60°角的三个小三角形都是全等形(如图7),从而.
设的延长线交于,因为.所以,由此得到与含30°角的,这就为运用已知条件中的“=5”创造出有利条件.
设,
则,,
.
,
,
=25.
由此得,即,
,故选B.
模型4圆周角定理及其推论(证略)
解4本题中有一特殊条件,是,解1就是通过建立“手拉手”全等模型,利用此特殊点得到一个直角三角形的.由此启发我们思考,还能通过其他方法,
利用此特殊点得到另一个直角三角形吗?
首先,考虑借助于什么几何模型,能够得到与、相等的角 因为同弧上的圆周角相等,自然会想到试用一下这个模塑.所以作或的外接圆⊙(如图8).
设的延长线分别交⊙于点,连结EF,由圆周角定理,得
.
同样,设的延长线交⊙于,连结,则
,
.
再连结,则是直角三角形.
接下来自然要想,的三条边与有没有数量关系 若有,
才能在解题中发挥作用.
观察图形,发现,
,设,
则.
,
又.
.
,
.
在中,,
即,
由此易得.故选B.
可见,运用几何模型,能快速找到问题的突破口,进而顺利解决问题.
本文借助一道2017年的全国数学竞赛题,展示五种几何模型的应用.
题目如图1,四边形中,是对角线,是等边三角形,,则的长为()
(A)
(B)4
(C)
(D)4.5
模型1“手拉手”全等模型
如图2,与都是等腰三角形,顶角分别为与,且,则.
下面就图2的(1)与(3)说明结论成立.
由题意,知,
又
(如图2(1)),
或
(如图2(3)),
.
解1因为是等边三角形,所以只需以(或以)为边作一个等边三角形,便构造出“手拉手”全等模型.
现以为边作等边(如图3),连结,则
.
,
.
在中,,
.故选B.
模型2“斜射影”相似模型
中,点在边上.若是直角,且,由射影定理,得
.
若是任意角,且(如图4),则结论仍成立.
这是因为当时,,
,即.
我们不妨将图4称为“斜射影”相似模型.
解2这里将与或联系起来是解题的关键,为此作于点.这样一来,使与共用一边,于是由勾股定理,得到与间的关系式
,
即.
显然,由该式欲得到结论,只需.
到此,使我们联想到“斜射影”相似模型.
因为式子与“3”相关,所以要依托去构造,对比图4,可在射线上取一点,使得.
那么如何得到这个30°角呢 图中已有60°角,所以只要有一个含60°角的直角三角形,即可得到30°角,因此延长交射线于点(如图5).
,
.
由“斜射影”相似模型,得
.
显然,,
.
据以上分析,得,故选B.
模型3“一线三等角”相似模型
如图6,直线上有三点,点在直线同侧,若
,则.
简证
.
又.
特别地,当与有一组对应边相等时,有.
解3因为,所以若在线段上取一点,使,则.故,从而,所以原问题转化为求的长.
另一方面,因为的顶点在直线上,且,所以若作的外接等边,则构造出三组“一线三等角”形,而且构造出的含60°角的三个小三角形都是全等形(如图7),从而.
设的延长线交于,因为.所以,由此得到与含30°角的,这就为运用已知条件中的“=5”创造出有利条件.
设,
则,,
.
,
,
=25.
由此得,即,
,故选B.
模型4圆周角定理及其推论(证略)
解4本题中有一特殊条件,是,解1就是通过建立“手拉手”全等模型,利用此特殊点得到一个直角三角形的.由此启发我们思考,还能通过其他方法,
利用此特殊点得到另一个直角三角形吗?
首先,考虑借助于什么几何模型,能够得到与、相等的角 因为同弧上的圆周角相等,自然会想到试用一下这个模塑.所以作或的外接圆⊙(如图8).
设的延长线分别交⊙于点,连结EF,由圆周角定理,得
.
同样,设的延长线交⊙于,连结,则
,
.
再连结,则是直角三角形.
接下来自然要想,的三条边与有没有数量关系 若有,
才能在解题中发挥作用.
观察图形,发现,
,设,
则.
,
又.
.
,
.
在中,,
即,
由此易得.故选B.
可见,运用几何模型,能快速找到问题的突破口,进而顺利解决问题.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
