江苏省南京市2016-2017学年高一数学下学期期末试卷(含解析)
文档属性
| 名称 | 江苏省南京市2016-2017学年高一数学下学期期末试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 334.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-05 21:56:00 | ||
图片预览




文档简介
2016-2017学年江苏省南京市高一(下)期末数学试卷
一、填空题(共14小题,每小题5分,满分70分)
1.直线y=x﹣2的倾斜角大小为
.
2.若数列{an}满足a1=1,且an+1=2an,n∈N
,则a6的值为
.
3.直线3x﹣4y﹣12=0在x轴、y轴上的截距之和为
.
4.在△ABC中,若a=,b=,A=120°,则B的大小为
.
5.不等式的解集是
.
6.函数y=sinx﹣cosx的最大值为
.
7.若函数y=x+,x∈(﹣2,+∞),则该函数的最小值为
.
8.如图,若正四棱锥P﹣ABCD的底面边长为2,斜高为,则该正四棱锥的体积为
.
9.若sin(θ+)=,θ∈(,),则cosθ的值为
.
10.已知a,b,c是三条不同的直线,α,β,γ是三个不同的平面,那么下列命题中正确的序号为
.
①若a⊥c,b⊥c,则a∥b;
②若α⊥γ,β⊥γ,则α∥β;
③若a⊥α,b⊥α,则a∥b;
④若a⊥α,α⊥β,则α∥β.
11.设等比数列{an}的公比q,前n项和为Sn.若S3,S2,S4成等差数列,则实数q的值为
.
12.已知关于x的不等式(x﹣1)(x﹣2a)>0(a∈R)的解集为A,集合B=(2,3).若B A,则a的取值范围为
.
13.已知数列{an}满足a1=1,且an+1﹣an=2n,n∈N
,若+19≤3n对任意n∈N
都成立,则实数λ的取值范围为
.
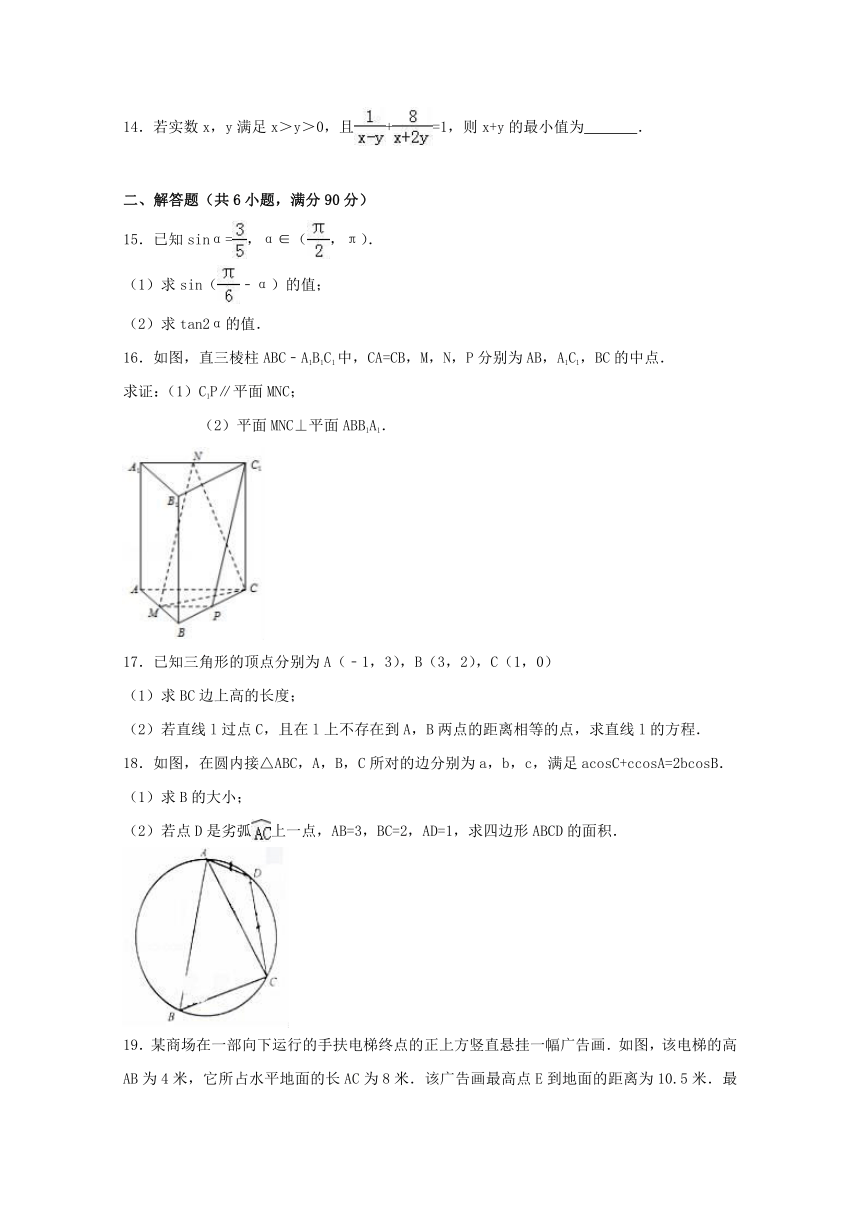
14.若实数x,y满足x>y>0,且+=1,则x+y的最小值为
.
二、解答题(共6小题,满分90分)
15.已知sinα=,α∈(,π).
(1)求sin(﹣α)的值;
(2)求tan2α的值.
16.如图,直三棱柱ABC﹣A1B1C1中,CA=CB,M,N,P分别为AB,A1C1,BC的中点.
求证:(1)C1P∥平面MNC;
(2)平面MNC⊥平面ABB1A1.
17.已知三角形的顶点分别为A(﹣1,3),B(3,2),C(1,0)
(1)求BC边上高的长度;
(2)若直线l过点C,且在l上不存在到A,B两点的距离相等的点,求直线l的方程.
18.如图,在圆内接△ABC,A,B,C所对的边分别为a,b,c,满足acosC+ccosA=2bcosB.
(1)求B的大小;
(2)若点D是劣弧上一点,AB=3,BC=2,AD=1,求四边形ABCD的面积.
19.某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高AB为4米,它所占水平地面的长AC为8米.该广告画最高点E到地面的距离为10.5米.最低点D到地面的距离6.5米.假设某人的眼睛到脚底的距离MN为1.5米,他竖直站在此电梯上观看DE的视角为θ.
(1)设此人到直线EC的距离为x米,试用x表示点M到地面的距离;
(2)此人到直线EC的距离为多少米,视角θ最大?
20.已知等差数列{an}和等比数列{bn},其中{an}的公差不为0.设Sn是数列{an}的前n项和.若a1,a2,a5是数列{bn}的前3项,且S4=16.
(1)求数列{an}和{bn}的通项公式;
(2)若数列{}为等差数列,求实数t;
(3)构造数列a1,b1,a2,b1,b2,a3,b1,b2,b3,…,ak,b1,b2,…,bk,…,若该数列前n项和Tn=1821,求n的值.
2016-2017学年江苏省南京市高一(下)期末数学试卷
参考答案与试题解析
一、填空题(共14小题,每小题5分,满分70分)
1.直线y=x﹣2的倾斜角大小为 60° .
【考点】I2:直线的倾斜角.
【分析】由于直线的斜率等于,设倾斜角等于α,则
0°≤α<180°,且tanα=,由此求得α的值
【解答】解:由题意得:直线的斜率是:k=,
设倾斜角等于α,则
0°≤α<180°,且tanα=,
∴α=60°,
故答案为
60°.
2.若数列{an}满足a1=1,且an+1=2an,n∈N
,则a6的值为 32 .
【考点】88:等比数列的通项公式.
【分析】利用等比数列的通项公式即可得出.
【解答】解:∵数列{an}满足a1=1,且an+1=2an,n∈N
,
则a6=1×25=32.
故答案为:32.
3.直线3x﹣4y﹣12=0在x轴、y轴上的截距之和为 1 .
【考点】IE:直线的截距式方程.
【分析】直线3x﹣4y﹣12=0化为截距式:
=1,即可得出.
【解答】解:直线3x﹣4y﹣12=0化为截距式:
=1,
∴直线3x﹣4y﹣12=0在x轴、y轴上的截距之和=4﹣3=1.
故答案为:1.
4.在△ABC中,若a=,b=,A=120°,则B的大小为 45° .
【考点】HP:正弦定理.
【分析】由已知及正弦定理可得sinB,结合b<a,B为锐角,即可得解B的值.
【解答】解:∵a=,b=,A=120°,
∴由正弦定理,可得:sinB===,
∵b<a,B为锐角,
∴B=45°.
故答案为:45°.
5.不等式的解集是 {x|﹣2<x<1} .
【考点】7E:其他不等式的解法.
【分析】由方程化为x﹣1与x+2的乘积为负数,得到x﹣1与x+2异号,转化为两个一元一次不等式组,求出不等式组的解集即可得到原不等式的解集.
【解答】解:方程化为(x﹣1)(x+2)<0,
即或,解得:﹣2<x<1,
则不等式的解集为{x|﹣2<x<1}.
故答案为:{x|﹣2<x<1}
6.函数y=sinx﹣cosx的最大值为 .
【考点】HW:三角函数的最值.
【分析】把给出的函数提取,由两角差的正弦公式化积,则函数的最大值可求.
【解答】解:∵y=sinx﹣cosx
=
=
=.
∴函数y=sinx﹣cosx的最大值为.
故答案为:
7.若函数y=x+,x∈(﹣2,+∞),则该函数的最小值为 4 .
【考点】7F:基本不等式.
【分析】变形利用基本不等式即可得出.
【解答】解:∵x∈(﹣2,+∞),
∴x+2>0
∴y=x+=x+2+﹣2≥2﹣2=6﹣2=4,当且仅当x=1时取等号,
故该函数的最小值为4,
故答案为:4
8.如图,若正四棱锥P﹣ABCD的底面边长为2,斜高为,则该正四棱锥的体积为 .
【考点】LF:棱柱、棱锥、棱台的体积.
【分析】利用已知中,正四棱锥底面正方形的边长为2,斜高为,求出正四棱锥的高PO,代入棱锥的体积公式,即可求得答案.
【解答】解:如图,正四棱锥的高PO,斜高PE,
则有PO=,
正四棱锥的体积为V==2,
故答案为:.
9.若sin(θ+)=,θ∈(,),则cosθ的值为 .
【考点】GI:三角函数的化简求值.
【分析】利用同角三角函数关系式以及和与差构造即可求解.
【解答】解:sin(θ+)=,利用和与差构造即可求解.
∵θ∈(,),
∴θ+∈(,π)
∴cos(θ+)=﹣.
那么:cosθ=cos=cos(θ+)cos+sinsin(θ+)==.
故答案为:.
10.已知a,b,c是三条不同的直线,α,β,γ是三个不同的平面,那么下列命题中正确的序号为 ③④ .
①若a⊥c,b⊥c,则a∥b;
②若α⊥γ,β⊥γ,则α∥β;
③若a⊥α,b⊥α,则a∥b;
④若a⊥α,α⊥β,则α∥β.
【考点】LP:空间中直线与平面之间的位置关系.
【分析】在①中,a与b相交、平行或异面;
在②中,α与β相交或平行;在③中,由线面垂直的性质定理得a∥b;在④中,由面面平行的判定定理得α∥β.
【解答】解:由a,b,c是三条不同的直线,α,β,γ是三个不同的平面,知:
在①中,若a⊥c,b⊥c,则a与b相交、平行或异面,故①错误;
在②中,若α⊥γ,β⊥γ,则α与β相交或平行,故②错误;
在③中,若a⊥α,b⊥α,则由线面垂直的性质定理得a∥b,故③正确;
在④中,若a⊥α,α⊥β,则由面面平行的判定定理得α∥β,故④正确.
故答案为:③④.
11.设等比数列{an}的公比q,前n项和为Sn.若S3,S2,S4成等差数列,则实数q的值为 ﹣2 .
【考点】88:等比数列的通项公式.
【分析】S3,S2,S4成等差数列,可得2S2=S3+S4,化为2a3+a4=0,即可得出.
【解答】解:∵S3,S2,S4成等差数列,∴2S2=S3+S4,∴2a3+a4=0,
可得q=﹣2.
故答案为:﹣2.
12.已知关于x的不等式(x﹣1)(x﹣2a)>0(a∈R)的解集为A,集合B=(2,3).若B A,则a的取值范围为 (﹣∞,1] .
【考点】18:集合的包含关系判断及应用.
【分析】对a分类讨论,利用不等式的解法、集合之间的基本关系即可得出.
【解答】解:关于x的不等式(x﹣1)(x﹣2a)>0(a∈R)的解集为A,
①2a≥1时,A=(﹣∞,1)∪(2a,+∞),∵B A,∴2a≤2,联立,解得.
②2a<1时,A=(﹣∞,2a)∪(1,+∞),满足B A,由2a<1,解得a.
综上可得:a的取值范围为(﹣∞,1].
故答案为:(﹣∞,1].
13.已知数列{an}满足a1=1,且an+1﹣an=2n,n∈N
,若+19≤3n对任意n∈N
都成立,则实数λ的取值范围为 (﹣∞,﹣8] .
【考点】8K:数列与不等式的综合.
【分析】a1=1,且an+1﹣an=2n,n∈N
,即n≥2时,an﹣an﹣1=2n﹣1.利用an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1可得an.
+19≤3n,化为:λ≤=f(n).
+19≤3n对任意n∈N
都成立, λ≤f(n)min.通过作差即可得出最小值.
【解答】解:∵a1=1,且an+1﹣an=2n,n∈N
,即n≥2时,an﹣an﹣1=2n﹣1.
∴an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1=2n﹣1+2n﹣2+…+2+1==2n﹣1.
∵+19≤3n,化为:λ≤=f(n).
+19≤3n对任意n∈N
都成立, λ≤f(n)min.
由f(n)≤0,可得n≤,因此n≤6时,f(n)<0;n≥7时,f(n)>0.
f(n+1)﹣f(n)=﹣=≤0,
解得n≤.
∴f(1)>f(2)>f(3)>f(4)>f(5)<f(6),
可得f(n)min=f(5)=﹣8.
则实数λ的取值范围为(﹣∞,﹣8].
故答案为:(﹣∞,﹣8].
14.若实数x,y满足x>y>0,且+=1,则x+y的最小值为 .
【考点】7F:基本不等式.
【分析】实数x,y满足x>y>0,且+=1,可得x+y===,利用基本不等式的性质即可得出.
【解答】解:实数x,y满足x>y>0,且+=1,
则x+y===≥=.
当且仅当y=,x=时取等号.
故答案为:.
二、解答题(共6小题,满分90分)
15.已知sinα=,α∈(,π).
(1)求sin(﹣α)的值;
(2)求tan2α的值.
【考点】GI:三角函数的化简求值.
【分析】(1)根据同角三角函数关系式以及和与差的公式计算即可.
(2)根据同角三角函数关系式以及二倍角公式计算.
【解答】解:∵sinα=,α∈(,π).
∴cosα==.
可得:tanα=.
(1)sin(﹣α)=sincosα﹣cossinα=×=.
(2)tan2α==.
16.如图,直三棱柱ABC﹣A1B1C1中,CA=CB,M,N,P分别为AB,A1C1,BC的中点.
求证:(1)C1P∥平面MNC;
(2)平面MNC⊥平面ABB1A1.
【考点】LY:平面与平面垂直的判定;LS:直线与平面平行的判定.
【分析】(1)连接MP,只需证明四边形MPC1N是平行四边形,即可得MN∥C1P∵C1P,即可证得C1P∥平面MNC;
(2)只需证明CM⊥平面MNC,即可得平面MNC⊥平面ABB1A1.
【解答】证明:(1)连接MP,因为M、P分别为AB,BC的中点
∵MP∥AC,MP=,
又因为在直三棱柱ABC﹣A1B1C1中,∴AC∥A1C1,AC=A1C1
且N是A1C1的中点,∴MP∥C1N,MP=C1N
∴四边形MPC1N是平行四边形,∴C1P∥MN
∵C1P 面MNC,MN 面MNC,∴C1P∥平面MNC;
(2)在△ABC中,CA=CB,M为AB的中点,∴CM⊥AB.
在直三棱柱ABC﹣A1B1C1中,B1B⊥面ABC.
∵CM 面ABC,∴BB1⊥CM
由因为BB1∩AB=B,BB1,AB 平面面ABB1A1
又CM 平面MNC,
∴平面MNC⊥平面ABB1A1.
17.已知三角形的顶点分别为A(﹣1,3),B(3,2),C(1,0)
(1)求BC边上高的长度;
(2)若直线l过点C,且在l上不存在到A,B两点的距离相等的点,求直线l的方程.
【考点】IK:待定系数法求直线方程.
【分析】(1)由条件利用直线的斜率公式,用点斜式求得直线BC的方程,再利用点到直线的距离公式求得BC边上高的长度.
(2)由题意可得直线l垂直于线段AB,求得直线AB的斜率,用点斜式求得直线l的方程.
【解答】解:(1)∵三角形的顶点分别为A(﹣1,3),B(3,2),C(1,0),
∴BC的斜率为=1,故直线BC的方程为y﹣0=1 (x﹣1),即
x﹣y﹣1=0,
故BC边上高的长度即点A到直线BC的距离,即=.
(2)∵直线l过点C,且在l上不存在到A,B两点的距离相等的点,∴直线l垂直于线段AB,
故直线l的斜率为==4,故直线l的方程为y﹣0=4 (x﹣1),即4x﹣y﹣4=0.
18.如图,在圆内接△ABC,A,B,C所对的边分别为a,b,c,满足acosC+ccosA=2bcosB.
(1)求B的大小;
(2)若点D是劣弧上一点,AB=3,BC=2,AD=1,求四边形ABCD的面积.
【考点】HT:三角形中的几何计算;NC:与圆有关的比例线段.
【分析】(1)根据正弦定理化简即可.
(2)在△ABC,利用余弦定理求出AC,已知B,可得∠ADC,再余弦定理求出DC,即可△ABC和△ADC面积,可得四边形ABCD的面积.
【解答】解:(1)∵acosC+ccosA=2bcosB.
由正弦定理,可得sinAcosC+sinAcosA=2sinBcosB.
得sinB=2sinBcosB.
∵0<B<π,sinB≠0,
∴cosB=,
即B=.
(2)在△ABC中,AB=3,BC=2,B=.
由余弦定理,cos=,
可得:AC=.
在△ADC中,AC=,AD=1,ABCD在圆上,
∵B=.
∴∠ADC=.
由余弦定理,cos==.
解得:DC=2
四边形ABCD的面积S=S△ABC+S△ADC=AD DC sin+AB BC sin=2.
19.某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高AB为4米,它所占水平地面的长AC为8米.该广告画最高点E到地面的距离为10.5米.最低点D到地面的距离6.5米.假设某人的眼睛到脚底的距离MN为1.5米,他竖直站在此电梯上观看DE的视角为θ.
(1)设此人到直线EC的距离为x米,试用x表示点M到地面的距离;
(2)此人到直线EC的距离为多少米,视角θ最大?
【考点】HU:解三角形的实际应用.
【分析】(1)根据相似三角形得出NH,从而得出MH;
(2)计算DG,EG,得出tan∠DMG和tan∠EMG,利用差角公式计算tanθ,得出tanθ关于x的解析式,利用不等式求出tanθ取得最大值时对应的x即可.
【解答】解:(1)由题意可知MG=CH=x,
由△CHN∽△CAB可得,即,
∴NH=,
∴M到地面的距离MH=MN+NH=.
(2)DG=CD﹣CG=CD﹣MH=5﹣,
同理EG=9﹣,
∴tan∠DMG==,tan∠EMG=,
∴tanθ=tan(∠EMG﹣∠DMG)===,
∵0<x≤8,∴5x+≥2=60,当且仅当5x=即x=6时取等号,
∴tanθ≤=,
∴当x=6时,tanθ取得最大值,即θ取得最大值.
20.已知等差数列{an}和等比数列{bn},其中{an}的公差不为0.设Sn是数列{an}的前n项和.若a1,a2,a5是数列{bn}的前3项,且S4=16.
(1)求数列{an}和{bn}的通项公式;
(2)若数列{}为等差数列,求实数t;
(3)构造数列a1,b1,a2,b1,b2,a3,b1,b2,b3,…,ak,b1,b2,…,bk,…,若该数列前n项和Tn=1821,求n的值.
【考点】8E:数列的求和;8H:数列递推式.
【分析】(1)设{an}的公差d≠0.由a1,a2,a5是数列{bn}的前3项,且S4=16.可得,即,4a1+=16,解得a1,d,即可得出.
(2)Sn==n2.可得=.根据数列{}为等差数列,可得=+,t2﹣2t=0.
解得t.
(3)由(1)可得:Sn=n2,数列{bn}的前n项和An==.数列{An}的前n项和Un=﹣n=﹣n.数列a1,b1,a2,b1,b2,a3,b1,b2,b3,…,ak,b1,b2,…,bk,…,可得:该数列前k+=项和=k2+﹣(k﹣1),根据37=2187,38=6561.进而得出.
【解答】解:(1)设{an}的公差d≠0.∵a1,a2,a5是数列{bn}的前3项,且S4=16.
∴,即,4a1+=16,
解得a1=1,d=2,
∴an=1+(n﹣1)×2=2n﹣1.
∴b1=1,b2=3,公比q=3.
∴bn=3n﹣1.
(2)Sn==n2.∴
=.
∵数列{}为等差数列,
∴=+,t2﹣2t=0.
解得t=2或0,经过验证满足题意.
(3)由(1)可得:Sn=n2,数列{bn}的前n项和An==.数列{An}的前n项和Un=﹣n=﹣n.
数列a1,b1,a2,b1,b2,a3,b1,b2,b3,…,ak,b1,b2,…,bk,…,
∴该数列前k+=项和=k2+﹣(k﹣1),
∵37=2187,38=6561.
∴取k=8,可得前=36项的和为:
=1700,
令Tn=1821=1700+,解得m=5.
∴n=36+5=41.
一、填空题(共14小题,每小题5分,满分70分)
1.直线y=x﹣2的倾斜角大小为
.
2.若数列{an}满足a1=1,且an+1=2an,n∈N
,则a6的值为
.
3.直线3x﹣4y﹣12=0在x轴、y轴上的截距之和为
.
4.在△ABC中,若a=,b=,A=120°,则B的大小为
.
5.不等式的解集是
.
6.函数y=sinx﹣cosx的最大值为
.
7.若函数y=x+,x∈(﹣2,+∞),则该函数的最小值为
.
8.如图,若正四棱锥P﹣ABCD的底面边长为2,斜高为,则该正四棱锥的体积为
.
9.若sin(θ+)=,θ∈(,),则cosθ的值为
.
10.已知a,b,c是三条不同的直线,α,β,γ是三个不同的平面,那么下列命题中正确的序号为
.
①若a⊥c,b⊥c,则a∥b;
②若α⊥γ,β⊥γ,则α∥β;
③若a⊥α,b⊥α,则a∥b;
④若a⊥α,α⊥β,则α∥β.
11.设等比数列{an}的公比q,前n项和为Sn.若S3,S2,S4成等差数列,则实数q的值为
.
12.已知关于x的不等式(x﹣1)(x﹣2a)>0(a∈R)的解集为A,集合B=(2,3).若B A,则a的取值范围为
.
13.已知数列{an}满足a1=1,且an+1﹣an=2n,n∈N
,若+19≤3n对任意n∈N
都成立,则实数λ的取值范围为
.
14.若实数x,y满足x>y>0,且+=1,则x+y的最小值为
.
二、解答题(共6小题,满分90分)
15.已知sinα=,α∈(,π).
(1)求sin(﹣α)的值;
(2)求tan2α的值.
16.如图,直三棱柱ABC﹣A1B1C1中,CA=CB,M,N,P分别为AB,A1C1,BC的中点.
求证:(1)C1P∥平面MNC;
(2)平面MNC⊥平面ABB1A1.
17.已知三角形的顶点分别为A(﹣1,3),B(3,2),C(1,0)
(1)求BC边上高的长度;
(2)若直线l过点C,且在l上不存在到A,B两点的距离相等的点,求直线l的方程.
18.如图,在圆内接△ABC,A,B,C所对的边分别为a,b,c,满足acosC+ccosA=2bcosB.
(1)求B的大小;
(2)若点D是劣弧上一点,AB=3,BC=2,AD=1,求四边形ABCD的面积.
19.某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高AB为4米,它所占水平地面的长AC为8米.该广告画最高点E到地面的距离为10.5米.最低点D到地面的距离6.5米.假设某人的眼睛到脚底的距离MN为1.5米,他竖直站在此电梯上观看DE的视角为θ.
(1)设此人到直线EC的距离为x米,试用x表示点M到地面的距离;
(2)此人到直线EC的距离为多少米,视角θ最大?
20.已知等差数列{an}和等比数列{bn},其中{an}的公差不为0.设Sn是数列{an}的前n项和.若a1,a2,a5是数列{bn}的前3项,且S4=16.
(1)求数列{an}和{bn}的通项公式;
(2)若数列{}为等差数列,求实数t;
(3)构造数列a1,b1,a2,b1,b2,a3,b1,b2,b3,…,ak,b1,b2,…,bk,…,若该数列前n项和Tn=1821,求n的值.
2016-2017学年江苏省南京市高一(下)期末数学试卷
参考答案与试题解析
一、填空题(共14小题,每小题5分,满分70分)
1.直线y=x﹣2的倾斜角大小为 60° .
【考点】I2:直线的倾斜角.
【分析】由于直线的斜率等于,设倾斜角等于α,则
0°≤α<180°,且tanα=,由此求得α的值
【解答】解:由题意得:直线的斜率是:k=,
设倾斜角等于α,则
0°≤α<180°,且tanα=,
∴α=60°,
故答案为
60°.
2.若数列{an}满足a1=1,且an+1=2an,n∈N
,则a6的值为 32 .
【考点】88:等比数列的通项公式.
【分析】利用等比数列的通项公式即可得出.
【解答】解:∵数列{an}满足a1=1,且an+1=2an,n∈N
,
则a6=1×25=32.
故答案为:32.
3.直线3x﹣4y﹣12=0在x轴、y轴上的截距之和为 1 .
【考点】IE:直线的截距式方程.
【分析】直线3x﹣4y﹣12=0化为截距式:
=1,即可得出.
【解答】解:直线3x﹣4y﹣12=0化为截距式:
=1,
∴直线3x﹣4y﹣12=0在x轴、y轴上的截距之和=4﹣3=1.
故答案为:1.
4.在△ABC中,若a=,b=,A=120°,则B的大小为 45° .
【考点】HP:正弦定理.
【分析】由已知及正弦定理可得sinB,结合b<a,B为锐角,即可得解B的值.
【解答】解:∵a=,b=,A=120°,
∴由正弦定理,可得:sinB===,
∵b<a,B为锐角,
∴B=45°.
故答案为:45°.
5.不等式的解集是 {x|﹣2<x<1} .
【考点】7E:其他不等式的解法.
【分析】由方程化为x﹣1与x+2的乘积为负数,得到x﹣1与x+2异号,转化为两个一元一次不等式组,求出不等式组的解集即可得到原不等式的解集.
【解答】解:方程化为(x﹣1)(x+2)<0,
即或,解得:﹣2<x<1,
则不等式的解集为{x|﹣2<x<1}.
故答案为:{x|﹣2<x<1}
6.函数y=sinx﹣cosx的最大值为 .
【考点】HW:三角函数的最值.
【分析】把给出的函数提取,由两角差的正弦公式化积,则函数的最大值可求.
【解答】解:∵y=sinx﹣cosx
=
=
=.
∴函数y=sinx﹣cosx的最大值为.
故答案为:
7.若函数y=x+,x∈(﹣2,+∞),则该函数的最小值为 4 .
【考点】7F:基本不等式.
【分析】变形利用基本不等式即可得出.
【解答】解:∵x∈(﹣2,+∞),
∴x+2>0
∴y=x+=x+2+﹣2≥2﹣2=6﹣2=4,当且仅当x=1时取等号,
故该函数的最小值为4,
故答案为:4
8.如图,若正四棱锥P﹣ABCD的底面边长为2,斜高为,则该正四棱锥的体积为 .
【考点】LF:棱柱、棱锥、棱台的体积.
【分析】利用已知中,正四棱锥底面正方形的边长为2,斜高为,求出正四棱锥的高PO,代入棱锥的体积公式,即可求得答案.
【解答】解:如图,正四棱锥的高PO,斜高PE,
则有PO=,
正四棱锥的体积为V==2,
故答案为:.
9.若sin(θ+)=,θ∈(,),则cosθ的值为 .
【考点】GI:三角函数的化简求值.
【分析】利用同角三角函数关系式以及和与差构造即可求解.
【解答】解:sin(θ+)=,利用和与差构造即可求解.
∵θ∈(,),
∴θ+∈(,π)
∴cos(θ+)=﹣.
那么:cosθ=cos=cos(θ+)cos+sinsin(θ+)==.
故答案为:.
10.已知a,b,c是三条不同的直线,α,β,γ是三个不同的平面,那么下列命题中正确的序号为 ③④ .
①若a⊥c,b⊥c,则a∥b;
②若α⊥γ,β⊥γ,则α∥β;
③若a⊥α,b⊥α,则a∥b;
④若a⊥α,α⊥β,则α∥β.
【考点】LP:空间中直线与平面之间的位置关系.
【分析】在①中,a与b相交、平行或异面;
在②中,α与β相交或平行;在③中,由线面垂直的性质定理得a∥b;在④中,由面面平行的判定定理得α∥β.
【解答】解:由a,b,c是三条不同的直线,α,β,γ是三个不同的平面,知:
在①中,若a⊥c,b⊥c,则a与b相交、平行或异面,故①错误;
在②中,若α⊥γ,β⊥γ,则α与β相交或平行,故②错误;
在③中,若a⊥α,b⊥α,则由线面垂直的性质定理得a∥b,故③正确;
在④中,若a⊥α,α⊥β,则由面面平行的判定定理得α∥β,故④正确.
故答案为:③④.
11.设等比数列{an}的公比q,前n项和为Sn.若S3,S2,S4成等差数列,则实数q的值为 ﹣2 .
【考点】88:等比数列的通项公式.
【分析】S3,S2,S4成等差数列,可得2S2=S3+S4,化为2a3+a4=0,即可得出.
【解答】解:∵S3,S2,S4成等差数列,∴2S2=S3+S4,∴2a3+a4=0,
可得q=﹣2.
故答案为:﹣2.
12.已知关于x的不等式(x﹣1)(x﹣2a)>0(a∈R)的解集为A,集合B=(2,3).若B A,则a的取值范围为 (﹣∞,1] .
【考点】18:集合的包含关系判断及应用.
【分析】对a分类讨论,利用不等式的解法、集合之间的基本关系即可得出.
【解答】解:关于x的不等式(x﹣1)(x﹣2a)>0(a∈R)的解集为A,
①2a≥1时,A=(﹣∞,1)∪(2a,+∞),∵B A,∴2a≤2,联立,解得.
②2a<1时,A=(﹣∞,2a)∪(1,+∞),满足B A,由2a<1,解得a.
综上可得:a的取值范围为(﹣∞,1].
故答案为:(﹣∞,1].
13.已知数列{an}满足a1=1,且an+1﹣an=2n,n∈N
,若+19≤3n对任意n∈N
都成立,则实数λ的取值范围为 (﹣∞,﹣8] .
【考点】8K:数列与不等式的综合.
【分析】a1=1,且an+1﹣an=2n,n∈N
,即n≥2时,an﹣an﹣1=2n﹣1.利用an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1可得an.
+19≤3n,化为:λ≤=f(n).
+19≤3n对任意n∈N
都成立, λ≤f(n)min.通过作差即可得出最小值.
【解答】解:∵a1=1,且an+1﹣an=2n,n∈N
,即n≥2时,an﹣an﹣1=2n﹣1.
∴an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1=2n﹣1+2n﹣2+…+2+1==2n﹣1.
∵+19≤3n,化为:λ≤=f(n).
+19≤3n对任意n∈N
都成立, λ≤f(n)min.
由f(n)≤0,可得n≤,因此n≤6时,f(n)<0;n≥7时,f(n)>0.
f(n+1)﹣f(n)=﹣=≤0,
解得n≤.
∴f(1)>f(2)>f(3)>f(4)>f(5)<f(6),
可得f(n)min=f(5)=﹣8.
则实数λ的取值范围为(﹣∞,﹣8].
故答案为:(﹣∞,﹣8].
14.若实数x,y满足x>y>0,且+=1,则x+y的最小值为 .
【考点】7F:基本不等式.
【分析】实数x,y满足x>y>0,且+=1,可得x+y===,利用基本不等式的性质即可得出.
【解答】解:实数x,y满足x>y>0,且+=1,
则x+y===≥=.
当且仅当y=,x=时取等号.
故答案为:.
二、解答题(共6小题,满分90分)
15.已知sinα=,α∈(,π).
(1)求sin(﹣α)的值;
(2)求tan2α的值.
【考点】GI:三角函数的化简求值.
【分析】(1)根据同角三角函数关系式以及和与差的公式计算即可.
(2)根据同角三角函数关系式以及二倍角公式计算.
【解答】解:∵sinα=,α∈(,π).
∴cosα==.
可得:tanα=.
(1)sin(﹣α)=sincosα﹣cossinα=×=.
(2)tan2α==.
16.如图,直三棱柱ABC﹣A1B1C1中,CA=CB,M,N,P分别为AB,A1C1,BC的中点.
求证:(1)C1P∥平面MNC;
(2)平面MNC⊥平面ABB1A1.
【考点】LY:平面与平面垂直的判定;LS:直线与平面平行的判定.
【分析】(1)连接MP,只需证明四边形MPC1N是平行四边形,即可得MN∥C1P∵C1P,即可证得C1P∥平面MNC;
(2)只需证明CM⊥平面MNC,即可得平面MNC⊥平面ABB1A1.
【解答】证明:(1)连接MP,因为M、P分别为AB,BC的中点
∵MP∥AC,MP=,
又因为在直三棱柱ABC﹣A1B1C1中,∴AC∥A1C1,AC=A1C1
且N是A1C1的中点,∴MP∥C1N,MP=C1N
∴四边形MPC1N是平行四边形,∴C1P∥MN
∵C1P 面MNC,MN 面MNC,∴C1P∥平面MNC;
(2)在△ABC中,CA=CB,M为AB的中点,∴CM⊥AB.
在直三棱柱ABC﹣A1B1C1中,B1B⊥面ABC.
∵CM 面ABC,∴BB1⊥CM
由因为BB1∩AB=B,BB1,AB 平面面ABB1A1
又CM 平面MNC,
∴平面MNC⊥平面ABB1A1.
17.已知三角形的顶点分别为A(﹣1,3),B(3,2),C(1,0)
(1)求BC边上高的长度;
(2)若直线l过点C,且在l上不存在到A,B两点的距离相等的点,求直线l的方程.
【考点】IK:待定系数法求直线方程.
【分析】(1)由条件利用直线的斜率公式,用点斜式求得直线BC的方程,再利用点到直线的距离公式求得BC边上高的长度.
(2)由题意可得直线l垂直于线段AB,求得直线AB的斜率,用点斜式求得直线l的方程.
【解答】解:(1)∵三角形的顶点分别为A(﹣1,3),B(3,2),C(1,0),
∴BC的斜率为=1,故直线BC的方程为y﹣0=1 (x﹣1),即
x﹣y﹣1=0,
故BC边上高的长度即点A到直线BC的距离,即=.
(2)∵直线l过点C,且在l上不存在到A,B两点的距离相等的点,∴直线l垂直于线段AB,
故直线l的斜率为==4,故直线l的方程为y﹣0=4 (x﹣1),即4x﹣y﹣4=0.
18.如图,在圆内接△ABC,A,B,C所对的边分别为a,b,c,满足acosC+ccosA=2bcosB.
(1)求B的大小;
(2)若点D是劣弧上一点,AB=3,BC=2,AD=1,求四边形ABCD的面积.
【考点】HT:三角形中的几何计算;NC:与圆有关的比例线段.
【分析】(1)根据正弦定理化简即可.
(2)在△ABC,利用余弦定理求出AC,已知B,可得∠ADC,再余弦定理求出DC,即可△ABC和△ADC面积,可得四边形ABCD的面积.
【解答】解:(1)∵acosC+ccosA=2bcosB.
由正弦定理,可得sinAcosC+sinAcosA=2sinBcosB.
得sinB=2sinBcosB.
∵0<B<π,sinB≠0,
∴cosB=,
即B=.
(2)在△ABC中,AB=3,BC=2,B=.
由余弦定理,cos=,
可得:AC=.
在△ADC中,AC=,AD=1,ABCD在圆上,
∵B=.
∴∠ADC=.
由余弦定理,cos==.
解得:DC=2
四边形ABCD的面积S=S△ABC+S△ADC=AD DC sin+AB BC sin=2.
19.某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高AB为4米,它所占水平地面的长AC为8米.该广告画最高点E到地面的距离为10.5米.最低点D到地面的距离6.5米.假设某人的眼睛到脚底的距离MN为1.5米,他竖直站在此电梯上观看DE的视角为θ.
(1)设此人到直线EC的距离为x米,试用x表示点M到地面的距离;
(2)此人到直线EC的距离为多少米,视角θ最大?
【考点】HU:解三角形的实际应用.
【分析】(1)根据相似三角形得出NH,从而得出MH;
(2)计算DG,EG,得出tan∠DMG和tan∠EMG,利用差角公式计算tanθ,得出tanθ关于x的解析式,利用不等式求出tanθ取得最大值时对应的x即可.
【解答】解:(1)由题意可知MG=CH=x,
由△CHN∽△CAB可得,即,
∴NH=,
∴M到地面的距离MH=MN+NH=.
(2)DG=CD﹣CG=CD﹣MH=5﹣,
同理EG=9﹣,
∴tan∠DMG==,tan∠EMG=,
∴tanθ=tan(∠EMG﹣∠DMG)===,
∵0<x≤8,∴5x+≥2=60,当且仅当5x=即x=6时取等号,
∴tanθ≤=,
∴当x=6时,tanθ取得最大值,即θ取得最大值.
20.已知等差数列{an}和等比数列{bn},其中{an}的公差不为0.设Sn是数列{an}的前n项和.若a1,a2,a5是数列{bn}的前3项,且S4=16.
(1)求数列{an}和{bn}的通项公式;
(2)若数列{}为等差数列,求实数t;
(3)构造数列a1,b1,a2,b1,b2,a3,b1,b2,b3,…,ak,b1,b2,…,bk,…,若该数列前n项和Tn=1821,求n的值.
【考点】8E:数列的求和;8H:数列递推式.
【分析】(1)设{an}的公差d≠0.由a1,a2,a5是数列{bn}的前3项,且S4=16.可得,即,4a1+=16,解得a1,d,即可得出.
(2)Sn==n2.可得=.根据数列{}为等差数列,可得=+,t2﹣2t=0.
解得t.
(3)由(1)可得:Sn=n2,数列{bn}的前n项和An==.数列{An}的前n项和Un=﹣n=﹣n.数列a1,b1,a2,b1,b2,a3,b1,b2,b3,…,ak,b1,b2,…,bk,…,可得:该数列前k+=项和=k2+﹣(k﹣1),根据37=2187,38=6561.进而得出.
【解答】解:(1)设{an}的公差d≠0.∵a1,a2,a5是数列{bn}的前3项,且S4=16.
∴,即,4a1+=16,
解得a1=1,d=2,
∴an=1+(n﹣1)×2=2n﹣1.
∴b1=1,b2=3,公比q=3.
∴bn=3n﹣1.
(2)Sn==n2.∴
=.
∵数列{}为等差数列,
∴=+,t2﹣2t=0.
解得t=2或0,经过验证满足题意.
(3)由(1)可得:Sn=n2,数列{bn}的前n项和An==.数列{An}的前n项和Un=﹣n=﹣n.
数列a1,b1,a2,b1,b2,a3,b1,b2,b3,…,ak,b1,b2,…,bk,…,
∴该数列前k+=项和=k2+﹣(k﹣1),
∵37=2187,38=6561.
∴取k=8,可得前=36项的和为:
=1700,
令Tn=1821=1700+,解得m=5.
∴n=36+5=41.
同课章节目录
