冀教版七年级数学上册第二章几何图形的初步认识检测题(word版含答案)
文档属性
| 名称 | 冀教版七年级数学上册第二章几何图形的初步认识检测题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 278.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-07 17:21:46 | ||
图片预览


文档简介
第二章
几何图形的初步认识检测题
一、填空题(每空2分,共36分):
1、圆锥是由_
___个面围成,其中__
__个平面,___
__个曲面。
2、在棱柱中,任何相邻的两个面的交线都叫做______,相邻的两个侧面的交线叫做_______。3、从一个多边形的某个顶点出发,分别连接这个点和其余各顶点,可以把这个多边形分割成十个三角形,则这个多边形的边数为_____。
4、伟大的数学家欧拉发现并证明的关于一个多面体的顶点(V)、棱数(E)、面数(F)之间关系的公式为_______________。
5、已知三棱柱有5个面6个顶点9条棱,四棱柱有6个面8个顶点12条棱,五棱柱有7个面10个顶点15条棱,……,由此可以推测n棱柱有_____个面,____个顶点,_____条侧棱。
6、圆柱的表面展开图是________________________(用语言描述)。
7、圆柱体的截面的形状可能是________________________。(至少写出两个,可以多写,但不要写错)
8、用小立方块搭一几何体,使得它的主视图和俯视图如图所示,这样的几何体最少要_____个立方块,最多要____个立方块。
9、已知一不透明的正方体的六个面上分别写着1至6六个数字,如图是我们能看到的三种情况,那么1和5的对面数字分别是____和_____。
10、写出两个三视图形状都一样的几何体:_______、_________。
二、选择题(每题3分,共24分):
11、下面几何体的截面图不可能是圆的是(
)
A
圆柱
B
圆锥
C
球
D
棱柱
12、棱柱的侧面都是(
)
A
三角形
B
长方形
C
五边形
D
菱形
13、圆锥的侧面展开图是(
)
A、
长方形
B
正方形
C
圆
D
扇形
14、一个直立在水平面上的圆柱体的主视图、俯视图、左视图分别是(
)
A
长方形
、圆、长方形
B
长方形、长方形、圆
C
圆、长方形、长方形
D
长方形、长主形、圆
15、将半圆绕它的直径旋转一周形成的几何体是(
)
A
圆柱
B
圆锥
C
球
D
正方体
16、正方体的截面不可能是(
)
A
四边形
B
五边形
C
六边形
D
七边形
17、如图,该物体的俯视图是(
)
18、下列平面图形中不能围成正方体的是(
)
三、解答题(共40分):
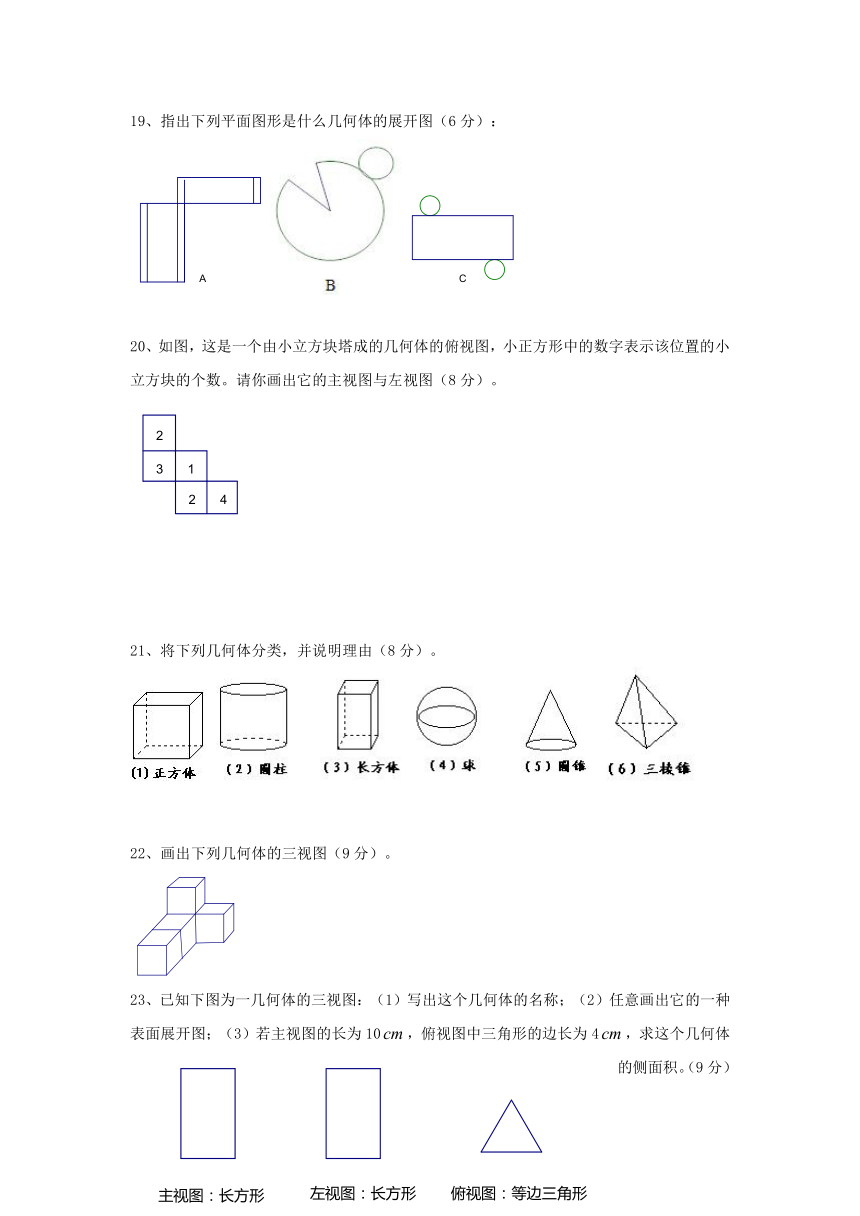
19、指出下列平面图形是什么几何体的展开图(6分):
20、如图,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数。请你画出它的主视图与左视图(8分)。
21、将下列几何体分类,并说明理由(8分)。
画出下列几何体的三视图(9分)。
23、已知下图为一几何体的三视图:(1)写出这个几何体的名称;(2)任意画出它的一种表面展开图;(3)若主视图的长为10,俯视图中三角形的边长为4,求这个几何体的侧面积。(9分)
选作题:
一、选择题:(每小题4分)
1、下列各图经过折叠后不能围成一个正方体的是
(
)
(A)
(B)
(C)
(D)
2、在下面的图形中是正方体的展开图的是
(
)
3、下列平面图形中不能围成正方体的是
(
)
A、
B、
C、
D、
二、(10分)探索规律:用棋子按下面的方式摆出正方形
①按图示规律填写下表:
图形编号
(1)
(2)
(3)
(4)
(5)
(6)
棋子个数
②按照这种方式摆下去,摆第个正方形需要多少个棋子?
③按照这种方式摆下去,第第个正方形需要多少个棋子?
参考答案:
一、1、2,1,1;
2、棱,侧棱;
3、12边;
4、
5、,,;
6、一个长方形和两个圆形;
7、圆、抛物线、长方形、正方形,椭圆形、梯形,只需2个即可;
8、9,13;
9、3,4;
10、球、正方体、正三棱锥;只需2个
二、
11、D;
12、B;
13、D;
14、A;
15、C;
16、D;
17、C;18、A;
三、
19、依次为:A
长方体;B
圆锥;
C
圆柱;
20、主视图和左视图依次为:
21、理由是:
(1)按平面分:正方体,长方体,三棱锥;
(2)按曲面分:圆柱,圆锥,球;其他分法,
合乎理由的酌情给分;
22、
23、(1)这个几何体的名称是三棱锥;
(2)任意一种图形:
(3)
选作题:
一、
1
、D;2、B;3、A;
二、
图形编号
(1)
(2)
(3)
(4)
(5)
(6)
棋子个数
4
8
12
16
20
24
(2)需要个棋子;(3)第20个正方形需要80个棋子;
(A)
(B)
(C)
(D)
几何图形的初步认识检测题
一、填空题(每空2分,共36分):
1、圆锥是由_
___个面围成,其中__
__个平面,___
__个曲面。
2、在棱柱中,任何相邻的两个面的交线都叫做______,相邻的两个侧面的交线叫做_______。3、从一个多边形的某个顶点出发,分别连接这个点和其余各顶点,可以把这个多边形分割成十个三角形,则这个多边形的边数为_____。
4、伟大的数学家欧拉发现并证明的关于一个多面体的顶点(V)、棱数(E)、面数(F)之间关系的公式为_______________。
5、已知三棱柱有5个面6个顶点9条棱,四棱柱有6个面8个顶点12条棱,五棱柱有7个面10个顶点15条棱,……,由此可以推测n棱柱有_____个面,____个顶点,_____条侧棱。
6、圆柱的表面展开图是________________________(用语言描述)。
7、圆柱体的截面的形状可能是________________________。(至少写出两个,可以多写,但不要写错)
8、用小立方块搭一几何体,使得它的主视图和俯视图如图所示,这样的几何体最少要_____个立方块,最多要____个立方块。
9、已知一不透明的正方体的六个面上分别写着1至6六个数字,如图是我们能看到的三种情况,那么1和5的对面数字分别是____和_____。
10、写出两个三视图形状都一样的几何体:_______、_________。
二、选择题(每题3分,共24分):
11、下面几何体的截面图不可能是圆的是(
)
A
圆柱
B
圆锥
C
球
D
棱柱
12、棱柱的侧面都是(
)
A
三角形
B
长方形
C
五边形
D
菱形
13、圆锥的侧面展开图是(
)
A、
长方形
B
正方形
C
圆
D
扇形
14、一个直立在水平面上的圆柱体的主视图、俯视图、左视图分别是(
)
A
长方形
、圆、长方形
B
长方形、长方形、圆
C
圆、长方形、长方形
D
长方形、长主形、圆
15、将半圆绕它的直径旋转一周形成的几何体是(
)
A
圆柱
B
圆锥
C
球
D
正方体
16、正方体的截面不可能是(
)
A
四边形
B
五边形
C
六边形
D
七边形
17、如图,该物体的俯视图是(
)
18、下列平面图形中不能围成正方体的是(
)
三、解答题(共40分):
19、指出下列平面图形是什么几何体的展开图(6分):
20、如图,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数。请你画出它的主视图与左视图(8分)。
21、将下列几何体分类,并说明理由(8分)。
画出下列几何体的三视图(9分)。
23、已知下图为一几何体的三视图:(1)写出这个几何体的名称;(2)任意画出它的一种表面展开图;(3)若主视图的长为10,俯视图中三角形的边长为4,求这个几何体的侧面积。(9分)
选作题:
一、选择题:(每小题4分)
1、下列各图经过折叠后不能围成一个正方体的是
(
)
(A)
(B)
(C)
(D)
2、在下面的图形中是正方体的展开图的是
(
)
3、下列平面图形中不能围成正方体的是
(
)
A、
B、
C、
D、
二、(10分)探索规律:用棋子按下面的方式摆出正方形
①按图示规律填写下表:
图形编号
(1)
(2)
(3)
(4)
(5)
(6)
棋子个数
②按照这种方式摆下去,摆第个正方形需要多少个棋子?
③按照这种方式摆下去,第第个正方形需要多少个棋子?
参考答案:
一、1、2,1,1;
2、棱,侧棱;
3、12边;
4、
5、,,;
6、一个长方形和两个圆形;
7、圆、抛物线、长方形、正方形,椭圆形、梯形,只需2个即可;
8、9,13;
9、3,4;
10、球、正方体、正三棱锥;只需2个
二、
11、D;
12、B;
13、D;
14、A;
15、C;
16、D;
17、C;18、A;
三、
19、依次为:A
长方体;B
圆锥;
C
圆柱;
20、主视图和左视图依次为:
21、理由是:
(1)按平面分:正方体,长方体,三棱锥;
(2)按曲面分:圆柱,圆锥,球;其他分法,
合乎理由的酌情给分;
22、
23、(1)这个几何体的名称是三棱锥;
(2)任意一种图形:
(3)
选作题:
一、
1
、D;2、B;3、A;
二、
图形编号
(1)
(2)
(3)
(4)
(5)
(6)
棋子个数
4
8
12
16
20
24
(2)需要个棋子;(3)第20个正方形需要80个棋子;
(A)
(B)
(C)
(D)
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
