直线与椭圆的位置关系专题讲座
图片预览









文档简介
课件31张PPT。直线与椭圆的位置关系专题高中数学教师欧阳文丰制作回忆:直线与圆的位置关系1.位置关系:相交、相切、相离
2.判别方法(代数法)
联立直线与圆的方程
消元得到二元一次方程组
(1)△>0?直线与圆相交?有两个公共点;
(2)△=0 ?直线与圆相切?有且只有一个公共点;
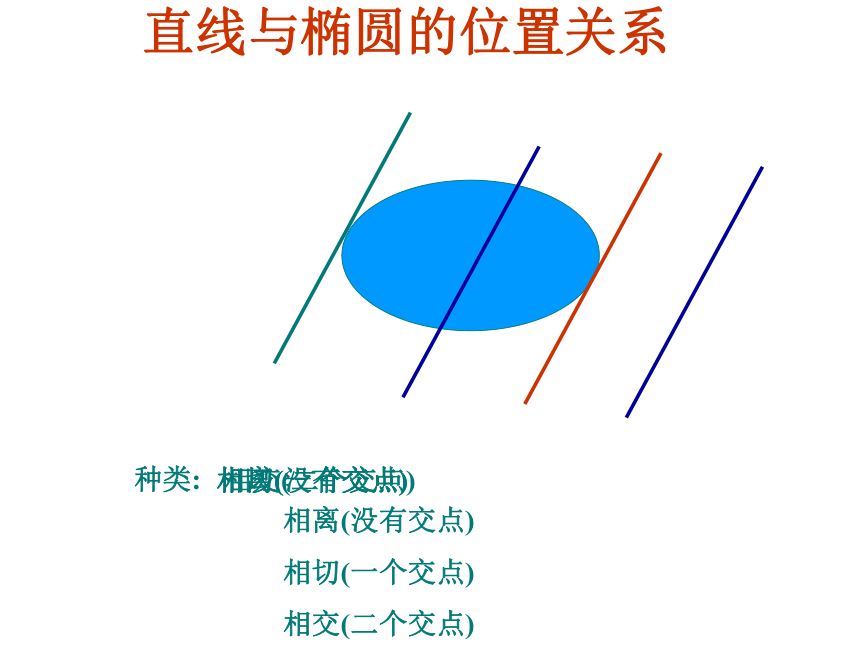
(3)△<0 ?直线与圆相离?无公共点.通法点与椭圆的位置关系直线与椭圆的位置关系种类:相离(没有交点)相切(一个交点)相交(二个交点)相离(没有交点)
相切(一个交点)
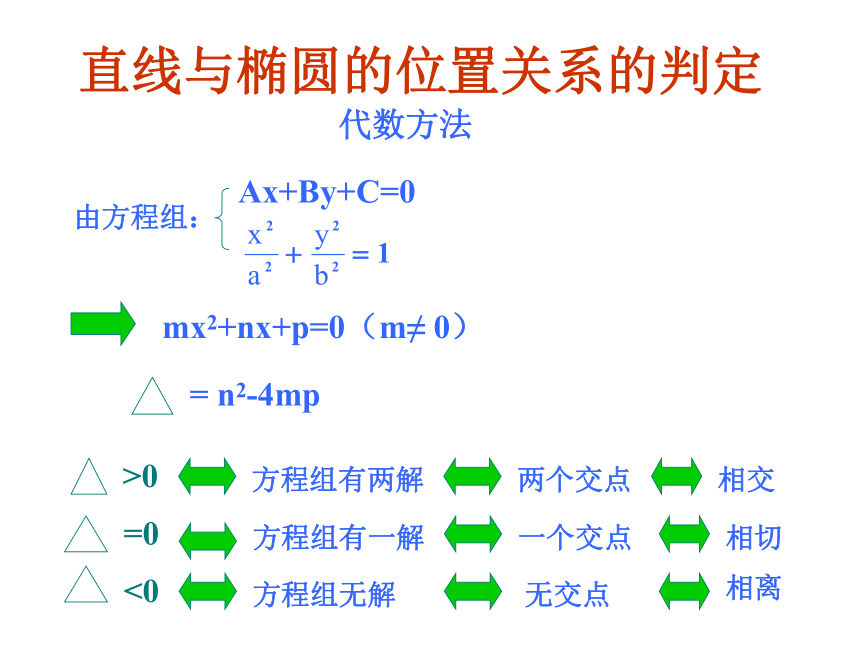
相交(二个交点) 直线与椭圆的位置关系的判定代数方法1.位置关系:相交、相切、相离
2.判别方法(代数法)
联立直线与椭圆的方程
消元得到二元一次方程组
(1)△>0?直线与椭圆相交?有两个公共点;
(2)△=0 ?直线与椭圆相切?有且只有一个公共点;
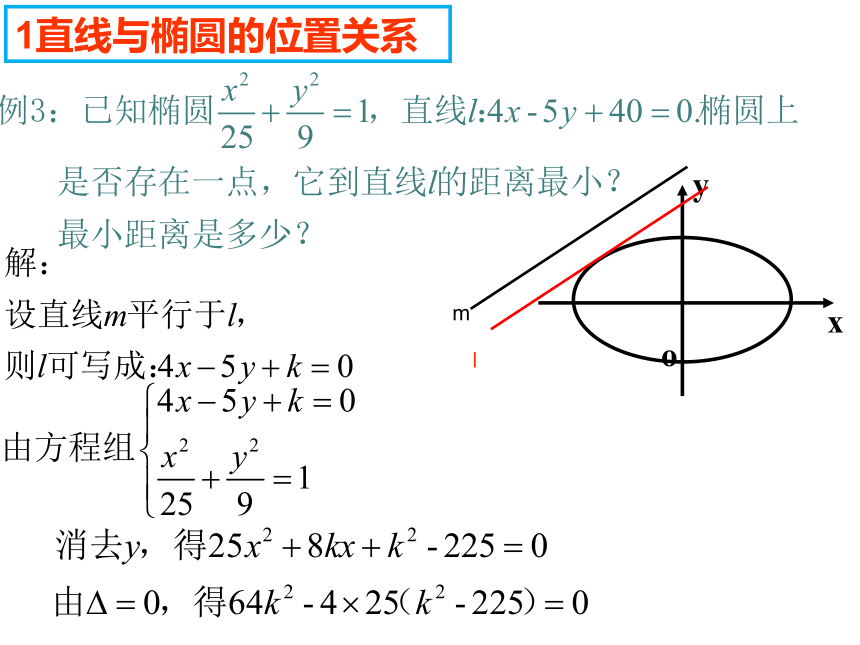
(3)△<0 ?直线与椭圆相离?无公共点.通法1直线与椭圆的位置关系例1.K为何值时,直线y=kx+2和曲线2x2+3y2=6有两个公共点?有一个公共点?没有公共点?D1直线与椭圆的位置关系1直线与椭圆的位置关系lm思考:最大的距离是多少?1直线与椭圆的位置关系ml解:联立方程组消去y?>0因为所以,方程(1)有两个根,那么,相交所得的弦的弦长是多少?则原方程组有两组解….----- (1)1直线与椭圆的位置关系设直线与椭圆交于P1(x1,y1),P2(x2,y2)两点,直线P1P2的斜率为k.2、弦长公式弦长公式:
例4:已知斜率为1的直线L过椭圆 的右焦点,
交椭圆于A,B两点,求弦AB之长.2、弦长公式练习、如图,已知椭圆 与直线x+y-1=0交
于A、B两点, AB的中点M与椭圆中心连线的
斜率是 ,试求a、b的值。点差法韦达定理例 :已知椭圆 过点P(2,1)引一弦,使弦在这点被
平分,求此弦所在直线的方程.解:韦达定理→斜率韦达定理法:利用韦达定理及中点坐标公式来构造3、弦中点问题韦达定理例 :已知椭圆 过点P(2,1)引一弦,使弦在这点被
平分,求此弦所在直线的方程.点差法:利用端点在曲线上,坐标满足方程,作差构造
出中点坐标和斜率.点作差3、弦中点问题点差法例:已知椭圆 过点P(2,1)引一弦,使弦在这点被
平分,求此弦所在直线的方程.所以 x2+4y2=(4-x)2+4(2-y)2,整理得x+2y-4=0
从而A ,B在直线x+2y-4=0上
而过A,B两点的直线有且只有一条解后反思:中点弦问题求解关键在于充分利用“中点”这一 条件,灵活运用中点坐标公式及韦达定理,3、弦中点问题3、弦中点问题的两种处理方法:
(1)联立方程组,消去一个未知数,利用韦达定理;
(2)设两端点坐标,代入曲线方程相减可求出弦的斜率。 1、直线与椭圆的三种位置关系及判断方法;小 结例4解:设椭圆上两点A(x1, y1), B(x2 , y2), AB的中点为C(x0,y0). 设直线AB方程为 【例5】试确定m的取值范围, 使得椭圆 上有不同两点A, B关于直线y=4x+m对称.
2.判别方法(代数法)
联立直线与圆的方程
消元得到二元一次方程组
(1)△>0?直线与圆相交?有两个公共点;
(2)△=0 ?直线与圆相切?有且只有一个公共点;
(3)△<0 ?直线与圆相离?无公共点.通法点与椭圆的位置关系直线与椭圆的位置关系种类:相离(没有交点)相切(一个交点)相交(二个交点)相离(没有交点)
相切(一个交点)
相交(二个交点) 直线与椭圆的位置关系的判定代数方法1.位置关系:相交、相切、相离
2.判别方法(代数法)
联立直线与椭圆的方程
消元得到二元一次方程组
(1)△>0?直线与椭圆相交?有两个公共点;
(2)△=0 ?直线与椭圆相切?有且只有一个公共点;
(3)△<0 ?直线与椭圆相离?无公共点.通法1直线与椭圆的位置关系例1.K为何值时,直线y=kx+2和曲线2x2+3y2=6有两个公共点?有一个公共点?没有公共点?D1直线与椭圆的位置关系1直线与椭圆的位置关系lm思考:最大的距离是多少?1直线与椭圆的位置关系ml解:联立方程组消去y?>0因为所以,方程(1)有两个根,那么,相交所得的弦的弦长是多少?则原方程组有两组解….----- (1)1直线与椭圆的位置关系设直线与椭圆交于P1(x1,y1),P2(x2,y2)两点,直线P1P2的斜率为k.2、弦长公式弦长公式:
例4:已知斜率为1的直线L过椭圆 的右焦点,
交椭圆于A,B两点,求弦AB之长.2、弦长公式练习、如图,已知椭圆 与直线x+y-1=0交
于A、B两点, AB的中点M与椭圆中心连线的
斜率是 ,试求a、b的值。点差法韦达定理例 :已知椭圆 过点P(2,1)引一弦,使弦在这点被
平分,求此弦所在直线的方程.解:韦达定理→斜率韦达定理法:利用韦达定理及中点坐标公式来构造3、弦中点问题韦达定理例 :已知椭圆 过点P(2,1)引一弦,使弦在这点被
平分,求此弦所在直线的方程.点差法:利用端点在曲线上,坐标满足方程,作差构造
出中点坐标和斜率.点作差3、弦中点问题点差法例:已知椭圆 过点P(2,1)引一弦,使弦在这点被
平分,求此弦所在直线的方程.所以 x2+4y2=(4-x)2+4(2-y)2,整理得x+2y-4=0
从而A ,B在直线x+2y-4=0上
而过A,B两点的直线有且只有一条解后反思:中点弦问题求解关键在于充分利用“中点”这一 条件,灵活运用中点坐标公式及韦达定理,3、弦中点问题3、弦中点问题的两种处理方法:
(1)联立方程组,消去一个未知数,利用韦达定理;
(2)设两端点坐标,代入曲线方程相减可求出弦的斜率。 1、直线与椭圆的三种位置关系及判断方法;小 结例4解:设椭圆上两点A(x1, y1), B(x2 , y2), AB的中点为C(x0,y0). 设直线AB方程为 【例5】试确定m的取值范围, 使得椭圆 上有不同两点A, B关于直线y=4x+m对称.
