7.2相交线 课件

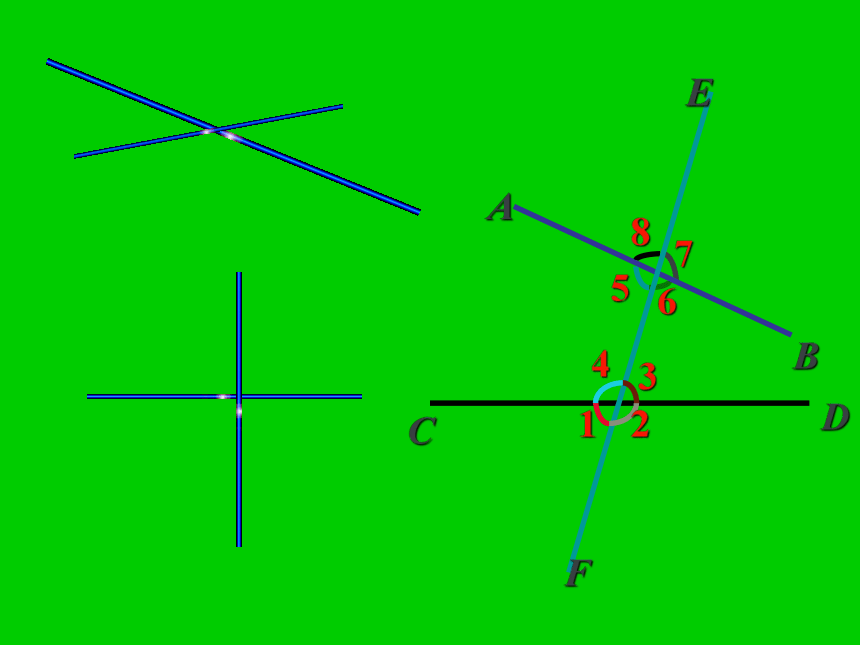
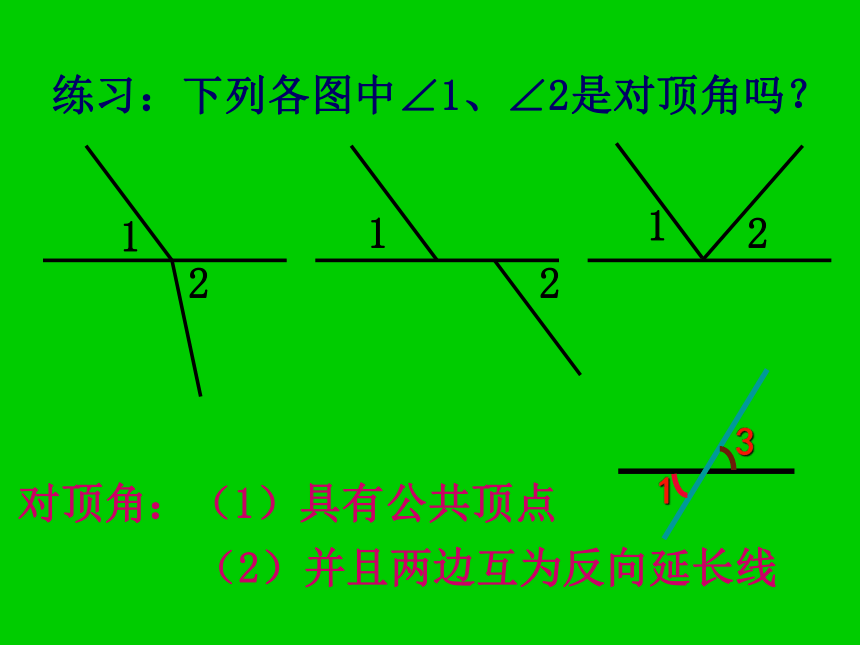
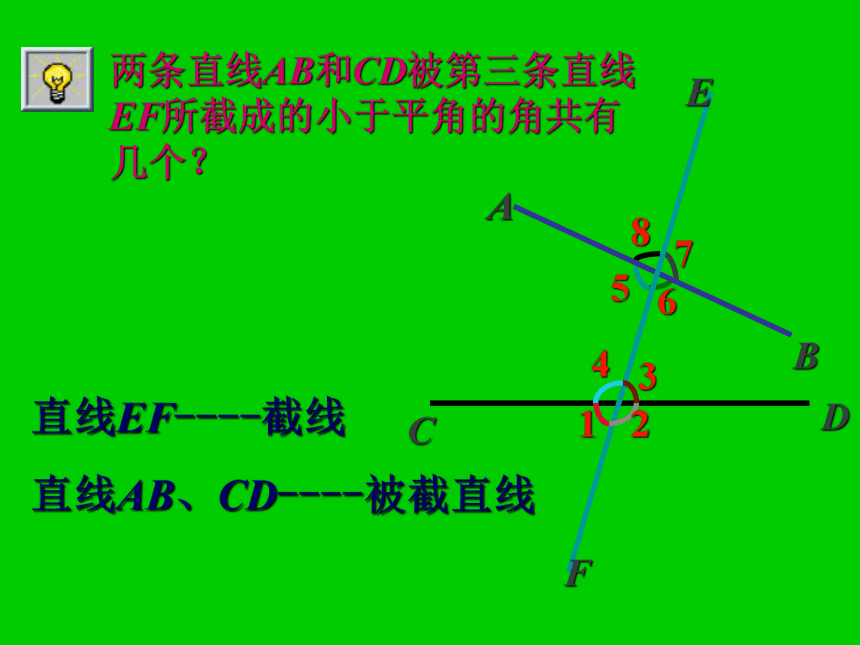
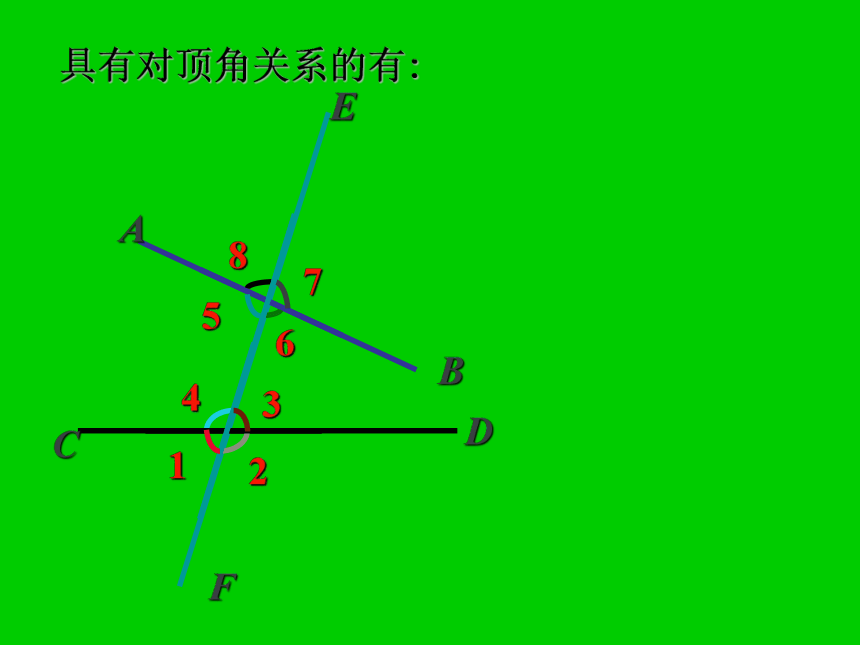
课件50张PPT。7.2 相交线（1） 两条直线CD和EF相交，能形成些具有什么关系的角？对顶角邻补角?练习：下列各图中∠1、∠2是对顶角吗？对顶角：（1）具有公共顶点（2）并且两边互为反向延长线对顶角的性质对顶角相等.2∠1与∠3的关系是_______.∠1与∠2的关系是_______.互补互补∠2与∠3的关系是_______.相等(3)有公共顶点且相等的两个角是对顶角.( )(5)对顶角的补角也相等 ( )两条直线相交，以交点为公共顶点的两角是对顶角. ( )(2)一个角与它的邻补角是有特殊关系的两个互补的角. ( )(4)两条相交直线构成的四个角中，不相邻的两个角是对顶角. ( ) ××√√√判断题直线EF----截线
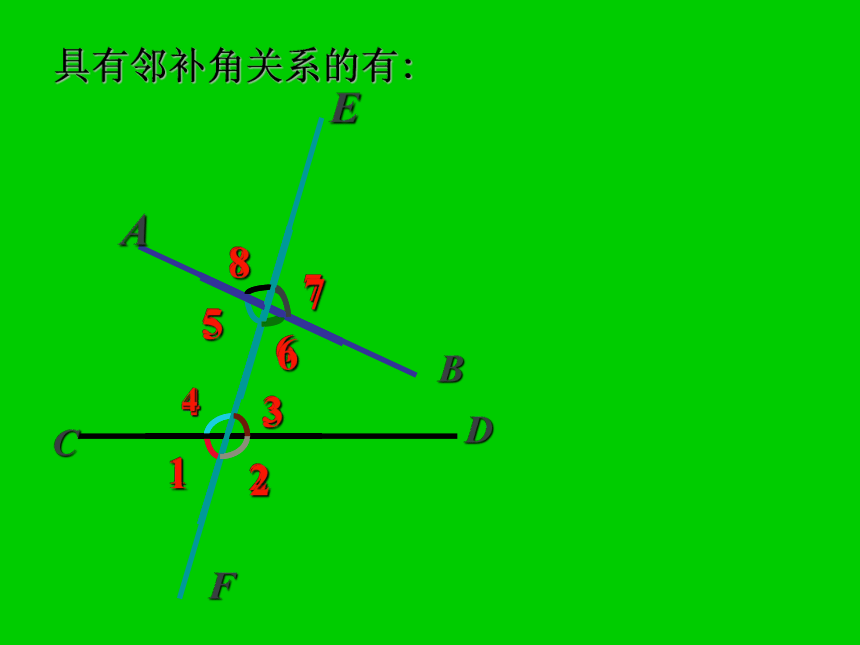
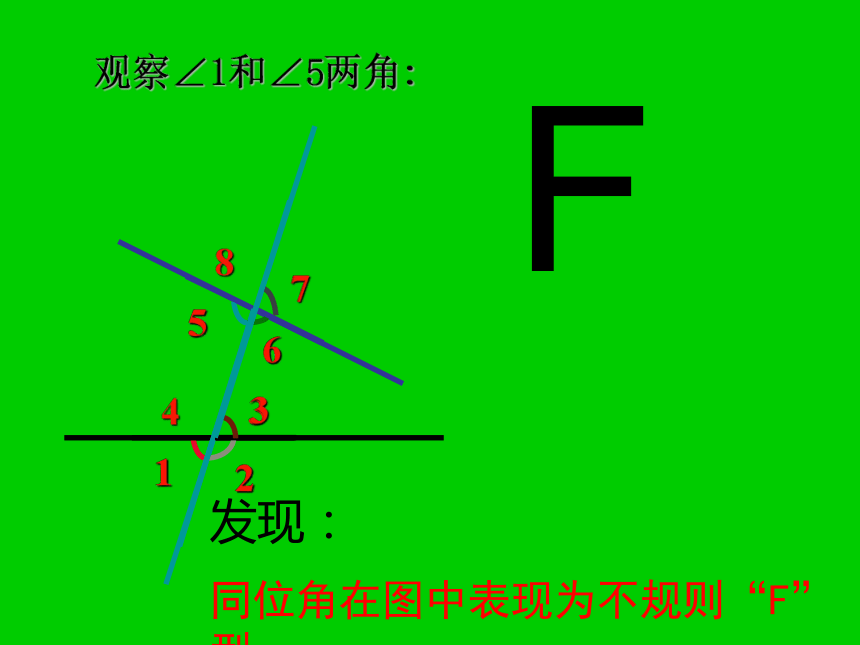
直线AB、CD----被截直线78541326具有邻补角关系的有:78541326具有对顶角关系的有:78541326观察∠1和∠5两角:F发现：
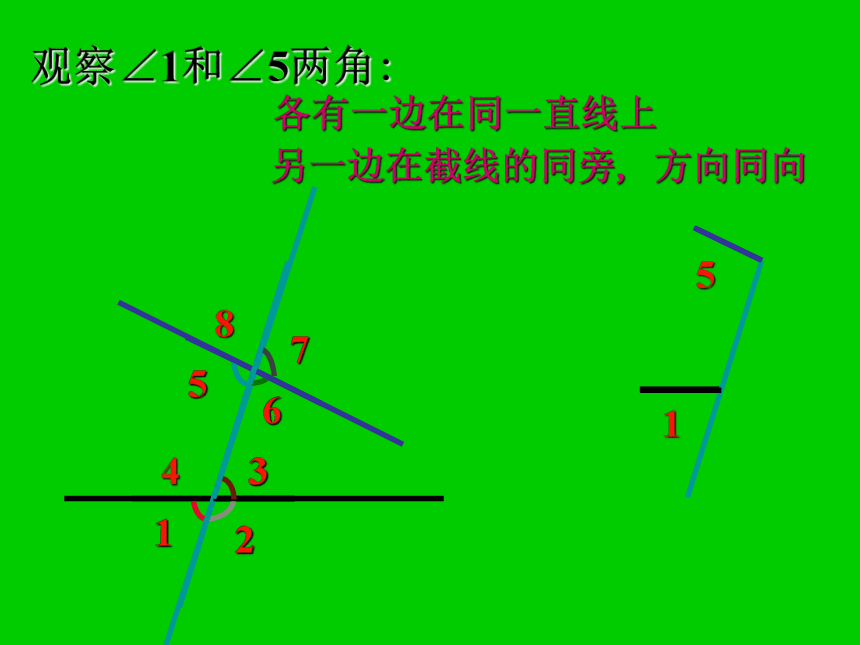
同位角在图中表现为不规则“F”型.7854132651各有一边在同一直线上观察∠1和∠5两角:另一边在截线的同旁, 方向同向一边都在截线上而且同向，另一边在截线同侧的两个角.同位角分别在截线的左侧,在被截直线的下方.观察∠1和∠5两角:78541326图中的同位角除∠1和∠5外，还有……78541326观察∠3和∠5两角：Z78541326各有一边在同一直线上53观察∠3和∠5两角：另一边在截线的两侧, 方向相反一边都在截线上而且反向，另一边在截线两侧的两个角内错角53观察∠3和∠5两角：夹在两被截直线内,分别在截线两侧(交错)78541326图中的内错角除∠3和∠5外，还有……78541326观察∠3和∠6：U78541326各有一边在同一直线上36观察∠3和∠6：另一边在截线的同旁, 方向相同一边都在截线上而且反向，另一边在截线同旁的两个角.同旁内角36观察∠3和∠6：在截线同旁,夹在两被截直线内.78541326图中的同旁内角除∠3和∠6外，还有……形如字母“U”在两条被截直线同旁，在截线同侧同旁内角形如字母“Z”
(或反置)在两条被截直线之内，在截线两侧(交错)内错角形如字母“F”
(不规则)在两条被截直线同旁，在截线同侧同位角图形结构特征位 置 特 征角的名称 请同学们分别用双手的大拇指，食指各组成一个角，两食指相对成一条线，保持在同一平面内，分别进行尝试，看可以组成哪些角．小游戏：练习：找出图中所有的同位角、内错角、同旁内角.1234567812345678同位角：∠1与∠5， ∠2与∠6，∠3与∠7， ∠4与∠8.12345678内错角： ∠3与∠5， ∠4与∠612345678同旁内角：∠3与∠6， ∠4与∠53241cba找出图中的同位角、内错角、同旁内角：找出图中的同位角、内错角 、同旁内角：FABCDE随堂练习12EDACB找出图中与∠1构成同旁内角的角?图中与∠1是同旁内角的角：如果我们用直线AB作直线EF和GH的截线时，就有：如果我们用直线EF
作直线AB和CD的
截线时，就有：
如果我们用直线AB作直线EF和GH的截线时，就有：如果我们用直线EF
作直线AB和CD的
截线时，就有：
QNPMACGEHFDB12345热热身竞 技 争 锋MQ请找出∠1的所有
的同位角答：∠1的同位角有
∠BME和 ∠DQF请找出∠1的所有
的内错角答：∠1的内错角有
∠AMF和 ∠CQE请找出∠1的所有
的同旁内角 答：∠1的同旁内角有
∠AME和 ∠CQF想想看竞 技 争 锋1DCAB243你能找出∠ 1的同位角 、内错角和同旁内角吗？同位角： ∠ 1和∠ 4内错角： 没有同旁内角：∠ 1和∠ 2 ， 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　∠ 1和∠ 3友情提示：在图形中不容易
找出截线和被截线时，我们
通常采用将射线反向延长或
将线段向两方向延长的方法
先确定截线和被截线，然后
寻找角之间的关系.步步高竞 技 争 锋相交线两条直线三条直线对顶角三线八角不相邻
同顶点
边反延
成双对同位角
内错角
同旁内角对顶角相等7.2 相交线（2）垂线的定义当两条直线所成的四个角中有一个角是直角时，我们就说这两条直线互相垂直。直线AB垂直于直线CD，O为垂足。
AB⊥CD，
O为垂足。含义1、∵AB⊥CD
∴∠1=90°含义2、∵∠1=90°
∴AB⊥CD小组议一议：（垂直用符号 “⊥”来表示，读作“垂直于” ）如图，CD ⊥EF， ∠1= ∠2，则AB⊥EF。请说明理由（补全解答过程）
解： ∵ CD ⊥EF（已知）
∴∠1= ____ ( )
∵ ∠1= ∠2=____
∴ AB___EF ( )90°⊥垂线的定义做一做：垂线的定义90° 如图，直线AB与直线CD相交于点O， OE⊥AB.已知∠BOD=45°求∠COE的度数。解：∵ OE⊥AB （已知）∴∠AOE=90°（垂线的定义）又∵ ∠ AOC=∠BOD=45 °∴ ∠COE=∠AOC+∠AOE
= 45°+90°=135°（对顶角的性质） 做一做：请用三角尺和量角器过点P画直线AB的垂线。PPA B A B QQ∴ PQ为所求∴ PQ为所求合作画一画：如果点P在直线上呢？请作图Q∴ PQ为所求合作画一画：画垂线的方法画垂线的方法可归纳为“一落、二过、三画”合作画一画：线段、射线的垂线应怎么画呢？A合作画一画：垂线的性质1：在同一平面内，过一点有且只有一条直线垂直于已知直线。结合以上的作图，请你思考：在同一平面内，过一点可以作几条直线与已知直线垂直？动脑想一想：BCEF垂线的性质2 :直线外一点与直线上各点连结的所有线段中，垂线段最短。点到直线上各点的线段长短比较点到直线的距离的概念 直线外一点到已知直线的垂线段的长度就叫做点到直线的距离。 如图，点P到直线AB的距离就是垂线段PQ的长度动脑想一想：如图是跳远沙坑示意图，在体育课上，老师是怎样测量同学们的跳远成绩的？你能尝试说明其中的理由吗？将尺子拉直与踏板边所在直线垂直，取最近的脚印后跟与踏板边沿之间的距离就是跳远成绩。
理由是：直线外一点与直线上各点连结的所有线段中，垂线段最短。动手练一练：1、如图，找出图中和线段AB、线段BC垂直的线段。变式练习：指出图中点A到直线CD、直线BC的距离是哪两条线段的长 ？2、如图，一辆汽车在一段笔直的公路上从M村开往N村，P村不在MN上。
（1）如果有一人想在M、N两村之间下车，前往P村，他在哪里下车走的路程最短？请画出图形，并说明你的想法。MNP动手练一练：（2）汽车在哪一段路上行驶时，与P村的距离越来越近？汽车在哪一段路上行驶时，与P村的距离越来越远？1. 理解了垂线的概念，会用三角尺、量角器过一点画一条直线的垂线；
2. 理解了点到直线的距离的概念，并会度量点到直线的距离。
3. 掌握了垂线的两个性质。今天你学到了什么?小结：你还有哪些困惑?