【备考2018】数学小升初考点分析(3)(含解析)
文档属性
| 名称 | 【备考2018】数学小升初考点分析(3)(含解析) | 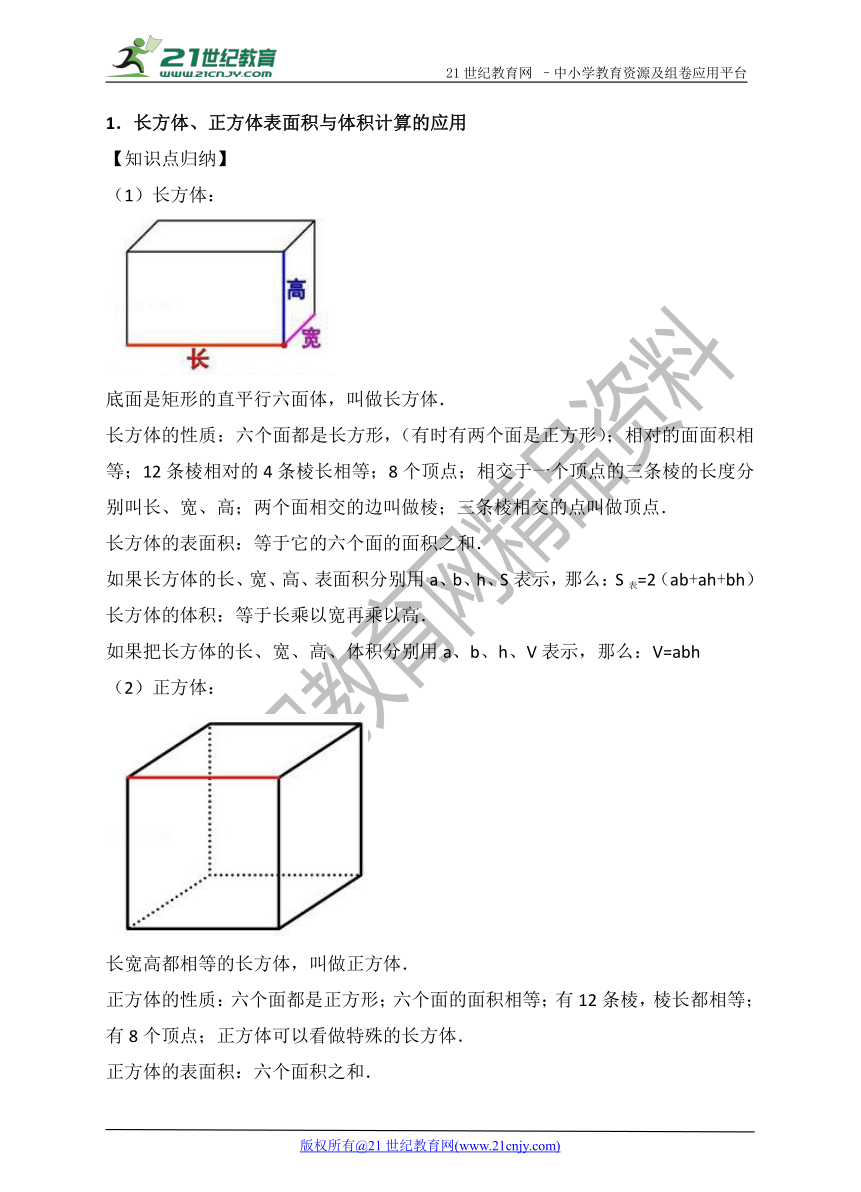 | |
| 格式 | doc | ||
| 文件大小 | 217.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-15 09:30:45 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
1.长方体、正方体表面积与体积计算的应用
【知识点归纳】
(1)长方体:
( http: / / www.21cnjy.com )
底面是矩形的直平行六面体,叫做长方体.
长方体的性质:六个面都是长方形,(有时有 ( http: / / www.21cnjy.com )两个面是正方形);相对的面面积相等;12条棱相对的4条棱长相等;8个顶点;相交于一个顶点的三条棱的长度分别叫长、宽、高;两个面相交的边叫做棱;三条棱相交的点叫做顶点.
长方体的表面积:等于它的六个面的面积之和.
如果长方体的长、宽、高、表面积分别用a、b、h、S表示,那么:S表=2(ab+ah+bh)
长方体的体积:等于长乘以宽再乘以高.
如果把长方体的长、宽、高、体积分别用a、b、h、V表示,那么:V=abh
(2)正方体:
( http: / / www.21cnjy.com )
长宽高都相等的长方体,叫做正方体.
正方体的性质:六个面都是正方形;六个面的面积相等;有12条棱,棱长都相等;有8个顶点;正方体可以看做特殊的长方体.www.21-cn-jy.com
正方体的表面积:六个面积之和.
如果正方体的棱长、表面积分别用a、S表示,那么:S表=6a2
正方体的体积:棱长乘以棱长再乘以棱长.
如果把正方体的棱长、体积分别用a、V表示,那么:V=a3
【命题方向】
常考题型:
例1:棱长是4厘米的正方体的表面积是 96 平方厘米,体积是 64 立方厘米,可以截成棱长是2厘米的正方体 8 个.21·cn·jy·com
分析:①根据正方体的表面积和体积公式即可求得其表面积和体积②抓住正方题分割前后的体积不变,即可得出小正方体的个数.【来源:21cnj*y.co*m】
解:4×4×6=96(平方厘米),
4×4×4=64(立方厘米),
2×2×2=8(立方厘米),
64÷8=8(个);
答:棱长是4厘米的正方体的表面积是96平方厘米,体积是64立方厘米,可以截成棱长是2厘米的正方体8个.【出处:21教育名师】
故答案为:96;64;8.
点评:此题考查了正方体表面积和体积公式的灵活应用,以及正方体分割的方法.
例2:学校要粉刷新教室.已知教室的长是8米 ( http: / / www.21cnjy.com ),宽6米,高是3米,扣除门窗的面积11.4平方米,如果每平方米需要花4元涂料费,粉刷这个教室需要花费多少元?21教育名师原创作品
分析:由题意可知:需要粉刷的面积为教室四面 ( http: / / www.21cnjy.com )墙壁和天花板的面积,利用长方体的表面积减去地面的面积和门窗面积即可;需要粉刷的面积乘每平方米花的钱数,就是粉刷这个教室需要的花费.
解:需要粉刷的面积:
(8×6+6×3+3×8)×2﹣8×6﹣11.4,
=(48+18+24)×2﹣48﹣11.4,
=90×2﹣59.4,
=180﹣59.4,
=120.6(平方米);
需要的花费:120.6×4=482.4(元);
答:粉刷这个教室需要花费482.4元.
点评:此题主要考查长方体的表面积的计算方法的实际应用,关键是弄清楚:需要粉刷的面积由哪几部分组成.
2.有关圆的应用题
【知识点归纳】
( http: / / www.21cnjy.com )
当一条线段绕着它的一个端点在平面内旋转一周时,它的另一个端点的轨迹叫做圆.
连接圆心和圆上的任意一点的线段叫做半径,字母表示为r;
通过圆心并且两端都在圆上的线段叫做直径,字母表示为d,直径所在的直线是圆的对称轴.
圆的性质:圆有无数条半径和无数条直径.
圆的周长=πd=2πr
圆的面积=πr2.
【命题方向】
常考题型:
例1:火车主动轮的半径是0.75米,如果每分钟转300周,每小时可行多少米?
分析:先求出主动轮转动一周所行的米数,即主动轮的周长.然后根据每分钟转动的周数求出每分钟行的米数,最后用每分钟行的米数乘60即可.
解:3.14×(0.75×2)×300×60,
=3.14×1.5×300×60,
=84780(米);
答:每小时可行84780米.
点评:解答此题的关键是求主动轮的周长,即主动轮转动一周所行的米数.
例2:为美化校园环境,学校 ( http: / / www.21cnjy.com )准备在周长是37.68米的花坛(如图)外围铺一条2米宽的环形小路,这条小路的面积是多少平方米?如果每平方米用水泥15千克,铺这条小路一共需要水泥多少千克?21cnjy.com
分析:在周长是37.68米的花坛(如图 ( http: / / www.21cnjy.com ))外围铺一条2米宽的环形小路,这条小路就是一个圆环,已知里圆的周长是37.68米,根据圆的周长公式c=2πr,求出半径r,外圆的半径就是r+2米,圆环的面积即可求出π(R2﹣r2);如果每平方米用水泥15千克,铺这条小路一共需要水泥多少千克,用乘法,面积乘15,即可得解.2·1·c·n·j·y
解:设花坛的半径为r,外圆的半径R,由圆的周长公式,则有:
2πr=37.68,
r=6(米),
R=r+2=6+2=8(米),
这条小路的面积是:
S=π(R2﹣r2),
=3.14×(82﹣62),
=87.92(平方米);
87.92×15=1318.8(千克);
答:这条小路的面积是87.92平方米,铺这条小路一共需要水泥1318.8千克.
点评:此题考查了有关圆的应用题,理清思路,灵活应用圆的周长公式和面积公式是解决此题的关键.
( http: / / www.21cnjy.com )
3.重叠问题
【知识点归纳】
【命题方向】
常考题型:
例1:甲班和乙班共83人,乙班和丙班共86人,丙班和丁班共88人,问甲班和丁班共多少人?
分析:根据题干分析可得,甲班+乙班 ( http: / / www.21cnjy.com )+丙班+丁班=83+88=171人,即甲班+丁班+(乙班+丙班)=171人,所以从171人里面减去乙班与丙班的人数,即可得出甲班与丁班的人数之和,据此即可解答.【来源:21·世纪·教育·网】
解:83+88﹣86
=171﹣86
=85(人)
答:甲班与丁班共有85人.
点评:解答此题的关键是明确83+88=171人是甲班、乙班、丙班、丁班的人数之和,据此再减去乙班与丙班的人数之和,即可得出答案.www-2-1-cnjy-com
例2:如图所示,阴影部分的面积是甲圆面积的 ( http: / / www.21cnjy.com ),是乙圆面积的 ( http: / / www.21cnjy.com ),乙圆的面积是甲圆的 ( http: / / www.21cnjy.com ) .
分析:此题把阴影部分的面积看作单位“1”,由“阴影部分面积是甲圆面积的 ( http: / / www.21cnjy.com )”,可知甲圆面积是阴影面积的1÷ ( http: / / www.21cnjy.com )=9(倍),由“阴影部分面积是乙圆面积的 ( http: / / www.21cnjy.com )”,可知乙圆面积是阴影面积的1÷ ( http: / / www.21cnjy.com )=4(倍);因此乙圆的面积是甲圆的4÷9= ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
4.简单的等量代换问题
【知识点归纳】
定义:用一种量(或一种量的一部分)来代替和它相等的另一种量(或另一种量的一部分).
“等量代换”是指一个量用与它相等的 ( http: / / www.21cnjy.com )量去代替,它是数学中一种基本的思想方法,也是代数思想方法的基础,狭义的等量代换思想用等式的性质来体现就是等式的传递性:如果a=b,b=c,那么a=c.21*cnjy*com
【命题方向】
常考题型:
例1:已知:△+△+△=☆,☆+☆+☆=□+□,那么△:□是( )
A、2:9 B、1:6 C、9:2 D、3:2 E、1:3
分析:由题意“三个△等于一个☆”知9个△等于3个☆,又因为“3个☆等于2个□,根据等量代换:9个△等于2个□,从而找出△与□的比.21·世纪*教育网
解:因为△+△+△=☆,
所以☆+☆+☆=△+△+△+△+△+△+△+△+△=3×3=9个△,
又因为☆+☆+☆=□+□,
所以9个△=2个□,
所以△:□=2:9.
故选:A.
点评:此题主要是根据3个△等于1个☆进行等量代换,找出△与□个数的比.
例2:粮店有大米20袋,面粉50袋,共重2250千克.已知1袋大米的重量和2袋面粉的重量相等,那么一袋大米重多少千克?21世纪教育网版权所有
分析:根据1袋大米的重量和2袋面粉的重量相等 ( http: / / www.21cnjy.com ),所以面粉50袋的重量和25袋大米的重量相等,所以20袋大米+25袋大米=2250千克,45袋大米的重量=2250千克,所以一袋大米的重量=50千克,据此解答即可.
解:因为1袋大米的重量和2袋面粉的重量相等,
所以面粉50袋的重量和25袋大米的重量相等,
所以20袋大米+25袋大米=2250千克,
45袋大米的重量=2250千克,
所以一袋大米的重量=50千克.
点评:此题考查简单的等量代 ( http: / / www.21cnjy.com )换,解决此题的关键是根据1袋大米的重量和2袋面粉的重量相等得出45袋大米的重量=2250千克,进而求出一袋大米的重量.
5.百分率应用题
【知识点归纳】
出勤率:
发芽率=发芽种子数÷试验种子数×100%
小麦的出粉率=面粉的重量÷小麦的重量×100%
产品的合格率=合格的产品数÷产品总数×100%
职工的出勤率=实际出勤人数÷应出勤人数×100%
【命题方向】
常考题型:
例1:一种树苗实验成活率是98%,为了保证成活380棵,至少要种多少棵树苗?
分析:首先理解“成活率”的概念,成活率是指成活的棵数占总棵数的百分比,即成活率= ( http: / / www.21cnjy.com )×100%.
已知成活率是98%,成活380棵,求至少要种多少棵,根据成活棵数÷成活率,即380÷98%,计算即可.21教育网
解:380÷98%,
=380÷0.98,
≈388(棵);
答:至少要种388棵树苗.
点评:此题考查了成活率的概念,同时应注意在处理结果时应该用“进一法”.
例2:一个商场打折销售, ( http: / / www.21cnjy.com )规定购买200元以下(包括200元)商品不打折,200元以上500元以下(包括500元)全部打九折,如购买500元以上的商品,就把500元以内(包括500元)的打九折,超出的打八折,一个人买了两次,分别用了134元、466元,那么如果他一次购买这些商品的话,可节省多少元?
分析:先分析销售的办法:
(1)200元以下(包括200元)商品不打折,这种方法最多付款200元;
(2)200元以上500元以下(包括500元)全部打九折,这一阶段最少付款200×90%=180(元);2-1-c-n-j-y
最多付款500×90%=450(元);
(3)如购买500元以上的商品,就把500元以内(包括500元)的打九折,超出500元的部分打八折;这一阶段最少付款450元.【版权所有:21教育】
134元<180元,说明原价就是134元,没有打折;
466元>450元;它属于第(3)种情 ( http: / / www.21cnjy.com )况,有500元打九折,付450元;剩下的打八折;所以加上134元后也属于此阶段优惠;把134元按照8折优惠的钱数就是可以节省的钱数.21*cnjy*com
解:200×90%=180(元);
134元<180元,说明原价就是134元,没有打折;
500×90%=450(元);
466>450;
一次购买134元可以按照8折优惠;
134×(1﹣80%),
=134×20%,
=26.8(元);
答:一次购买可节省26.8元.
点评:本题考查了分类讨论的思想的运用:分析实际付款可按不同方式打折.也考查了实际生活中的折扣问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
1.长方体、正方体表面积与体积计算的应用
【知识点归纳】
(1)长方体:
( http: / / www.21cnjy.com )
底面是矩形的直平行六面体,叫做长方体.
长方体的性质:六个面都是长方形,(有时有 ( http: / / www.21cnjy.com )两个面是正方形);相对的面面积相等;12条棱相对的4条棱长相等;8个顶点;相交于一个顶点的三条棱的长度分别叫长、宽、高;两个面相交的边叫做棱;三条棱相交的点叫做顶点.
长方体的表面积:等于它的六个面的面积之和.
如果长方体的长、宽、高、表面积分别用a、b、h、S表示,那么:S表=2(ab+ah+bh)
长方体的体积:等于长乘以宽再乘以高.
如果把长方体的长、宽、高、体积分别用a、b、h、V表示,那么:V=abh
(2)正方体:
( http: / / www.21cnjy.com )
长宽高都相等的长方体,叫做正方体.
正方体的性质:六个面都是正方形;六个面的面积相等;有12条棱,棱长都相等;有8个顶点;正方体可以看做特殊的长方体.www.21-cn-jy.com
正方体的表面积:六个面积之和.
如果正方体的棱长、表面积分别用a、S表示,那么:S表=6a2
正方体的体积:棱长乘以棱长再乘以棱长.
如果把正方体的棱长、体积分别用a、V表示,那么:V=a3
【命题方向】
常考题型:
例1:棱长是4厘米的正方体的表面积是 96 平方厘米,体积是 64 立方厘米,可以截成棱长是2厘米的正方体 8 个.21·cn·jy·com
分析:①根据正方体的表面积和体积公式即可求得其表面积和体积②抓住正方题分割前后的体积不变,即可得出小正方体的个数.【来源:21cnj*y.co*m】
解:4×4×6=96(平方厘米),
4×4×4=64(立方厘米),
2×2×2=8(立方厘米),
64÷8=8(个);
答:棱长是4厘米的正方体的表面积是96平方厘米,体积是64立方厘米,可以截成棱长是2厘米的正方体8个.【出处:21教育名师】
故答案为:96;64;8.
点评:此题考查了正方体表面积和体积公式的灵活应用,以及正方体分割的方法.
例2:学校要粉刷新教室.已知教室的长是8米 ( http: / / www.21cnjy.com ),宽6米,高是3米,扣除门窗的面积11.4平方米,如果每平方米需要花4元涂料费,粉刷这个教室需要花费多少元?21教育名师原创作品
分析:由题意可知:需要粉刷的面积为教室四面 ( http: / / www.21cnjy.com )墙壁和天花板的面积,利用长方体的表面积减去地面的面积和门窗面积即可;需要粉刷的面积乘每平方米花的钱数,就是粉刷这个教室需要的花费.
解:需要粉刷的面积:
(8×6+6×3+3×8)×2﹣8×6﹣11.4,
=(48+18+24)×2﹣48﹣11.4,
=90×2﹣59.4,
=180﹣59.4,
=120.6(平方米);
需要的花费:120.6×4=482.4(元);
答:粉刷这个教室需要花费482.4元.
点评:此题主要考查长方体的表面积的计算方法的实际应用,关键是弄清楚:需要粉刷的面积由哪几部分组成.
2.有关圆的应用题
【知识点归纳】
( http: / / www.21cnjy.com )
当一条线段绕着它的一个端点在平面内旋转一周时,它的另一个端点的轨迹叫做圆.
连接圆心和圆上的任意一点的线段叫做半径,字母表示为r;
通过圆心并且两端都在圆上的线段叫做直径,字母表示为d,直径所在的直线是圆的对称轴.
圆的性质:圆有无数条半径和无数条直径.
圆的周长=πd=2πr
圆的面积=πr2.
【命题方向】
常考题型:
例1:火车主动轮的半径是0.75米,如果每分钟转300周,每小时可行多少米?
分析:先求出主动轮转动一周所行的米数,即主动轮的周长.然后根据每分钟转动的周数求出每分钟行的米数,最后用每分钟行的米数乘60即可.
解:3.14×(0.75×2)×300×60,
=3.14×1.5×300×60,
=84780(米);
答:每小时可行84780米.
点评:解答此题的关键是求主动轮的周长,即主动轮转动一周所行的米数.
例2:为美化校园环境,学校 ( http: / / www.21cnjy.com )准备在周长是37.68米的花坛(如图)外围铺一条2米宽的环形小路,这条小路的面积是多少平方米?如果每平方米用水泥15千克,铺这条小路一共需要水泥多少千克?21cnjy.com
分析:在周长是37.68米的花坛(如图 ( http: / / www.21cnjy.com ))外围铺一条2米宽的环形小路,这条小路就是一个圆环,已知里圆的周长是37.68米,根据圆的周长公式c=2πr,求出半径r,外圆的半径就是r+2米,圆环的面积即可求出π(R2﹣r2);如果每平方米用水泥15千克,铺这条小路一共需要水泥多少千克,用乘法,面积乘15,即可得解.2·1·c·n·j·y
解:设花坛的半径为r,外圆的半径R,由圆的周长公式,则有:
2πr=37.68,
r=6(米),
R=r+2=6+2=8(米),
这条小路的面积是:
S=π(R2﹣r2),
=3.14×(82﹣62),
=87.92(平方米);
87.92×15=1318.8(千克);
答:这条小路的面积是87.92平方米,铺这条小路一共需要水泥1318.8千克.
点评:此题考查了有关圆的应用题,理清思路,灵活应用圆的周长公式和面积公式是解决此题的关键.
( http: / / www.21cnjy.com )
3.重叠问题
【知识点归纳】
【命题方向】
常考题型:
例1:甲班和乙班共83人,乙班和丙班共86人,丙班和丁班共88人,问甲班和丁班共多少人?
分析:根据题干分析可得,甲班+乙班 ( http: / / www.21cnjy.com )+丙班+丁班=83+88=171人,即甲班+丁班+(乙班+丙班)=171人,所以从171人里面减去乙班与丙班的人数,即可得出甲班与丁班的人数之和,据此即可解答.【来源:21·世纪·教育·网】
解:83+88﹣86
=171﹣86
=85(人)
答:甲班与丁班共有85人.
点评:解答此题的关键是明确83+88=171人是甲班、乙班、丙班、丁班的人数之和,据此再减去乙班与丙班的人数之和,即可得出答案.www-2-1-cnjy-com
例2:如图所示,阴影部分的面积是甲圆面积的 ( http: / / www.21cnjy.com ),是乙圆面积的 ( http: / / www.21cnjy.com ),乙圆的面积是甲圆的 ( http: / / www.21cnjy.com ) .
分析:此题把阴影部分的面积看作单位“1”,由“阴影部分面积是甲圆面积的 ( http: / / www.21cnjy.com )”,可知甲圆面积是阴影面积的1÷ ( http: / / www.21cnjy.com )=9(倍),由“阴影部分面积是乙圆面积的 ( http: / / www.21cnjy.com )”,可知乙圆面积是阴影面积的1÷ ( http: / / www.21cnjy.com )=4(倍);因此乙圆的面积是甲圆的4÷9= ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
4.简单的等量代换问题
【知识点归纳】
定义:用一种量(或一种量的一部分)来代替和它相等的另一种量(或另一种量的一部分).
“等量代换”是指一个量用与它相等的 ( http: / / www.21cnjy.com )量去代替,它是数学中一种基本的思想方法,也是代数思想方法的基础,狭义的等量代换思想用等式的性质来体现就是等式的传递性:如果a=b,b=c,那么a=c.21*cnjy*com
【命题方向】
常考题型:
例1:已知:△+△+△=☆,☆+☆+☆=□+□,那么△:□是( )
A、2:9 B、1:6 C、9:2 D、3:2 E、1:3
分析:由题意“三个△等于一个☆”知9个△等于3个☆,又因为“3个☆等于2个□,根据等量代换:9个△等于2个□,从而找出△与□的比.21·世纪*教育网
解:因为△+△+△=☆,
所以☆+☆+☆=△+△+△+△+△+△+△+△+△=3×3=9个△,
又因为☆+☆+☆=□+□,
所以9个△=2个□,
所以△:□=2:9.
故选:A.
点评:此题主要是根据3个△等于1个☆进行等量代换,找出△与□个数的比.
例2:粮店有大米20袋,面粉50袋,共重2250千克.已知1袋大米的重量和2袋面粉的重量相等,那么一袋大米重多少千克?21世纪教育网版权所有
分析:根据1袋大米的重量和2袋面粉的重量相等 ( http: / / www.21cnjy.com ),所以面粉50袋的重量和25袋大米的重量相等,所以20袋大米+25袋大米=2250千克,45袋大米的重量=2250千克,所以一袋大米的重量=50千克,据此解答即可.
解:因为1袋大米的重量和2袋面粉的重量相等,
所以面粉50袋的重量和25袋大米的重量相等,
所以20袋大米+25袋大米=2250千克,
45袋大米的重量=2250千克,
所以一袋大米的重量=50千克.
点评:此题考查简单的等量代 ( http: / / www.21cnjy.com )换,解决此题的关键是根据1袋大米的重量和2袋面粉的重量相等得出45袋大米的重量=2250千克,进而求出一袋大米的重量.
5.百分率应用题
【知识点归纳】
出勤率:
发芽率=发芽种子数÷试验种子数×100%
小麦的出粉率=面粉的重量÷小麦的重量×100%
产品的合格率=合格的产品数÷产品总数×100%
职工的出勤率=实际出勤人数÷应出勤人数×100%
【命题方向】
常考题型:
例1:一种树苗实验成活率是98%,为了保证成活380棵,至少要种多少棵树苗?
分析:首先理解“成活率”的概念,成活率是指成活的棵数占总棵数的百分比,即成活率= ( http: / / www.21cnjy.com )×100%.
已知成活率是98%,成活380棵,求至少要种多少棵,根据成活棵数÷成活率,即380÷98%,计算即可.21教育网
解:380÷98%,
=380÷0.98,
≈388(棵);
答:至少要种388棵树苗.
点评:此题考查了成活率的概念,同时应注意在处理结果时应该用“进一法”.
例2:一个商场打折销售, ( http: / / www.21cnjy.com )规定购买200元以下(包括200元)商品不打折,200元以上500元以下(包括500元)全部打九折,如购买500元以上的商品,就把500元以内(包括500元)的打九折,超出的打八折,一个人买了两次,分别用了134元、466元,那么如果他一次购买这些商品的话,可节省多少元?
分析:先分析销售的办法:
(1)200元以下(包括200元)商品不打折,这种方法最多付款200元;
(2)200元以上500元以下(包括500元)全部打九折,这一阶段最少付款200×90%=180(元);2-1-c-n-j-y
最多付款500×90%=450(元);
(3)如购买500元以上的商品,就把500元以内(包括500元)的打九折,超出500元的部分打八折;这一阶段最少付款450元.【版权所有:21教育】
134元<180元,说明原价就是134元,没有打折;
466元>450元;它属于第(3)种情 ( http: / / www.21cnjy.com )况,有500元打九折,付450元;剩下的打八折;所以加上134元后也属于此阶段优惠;把134元按照8折优惠的钱数就是可以节省的钱数.21*cnjy*com
解:200×90%=180(元);
134元<180元,说明原价就是134元,没有打折;
500×90%=450(元);
466>450;
一次购买134元可以按照8折优惠;
134×(1﹣80%),
=134×20%,
=26.8(元);
答:一次购买可节省26.8元.
点评:本题考查了分类讨论的思想的运用:分析实际付款可按不同方式打折.也考查了实际生活中的折扣问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
