陕西省2016-2017学年高二数学下学期期末试卷文(含解析)
文档属性
| 名称 | 陕西省2016-2017学年高二数学下学期期末试卷文(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 260.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-15 22:06:08 | ||
图片预览



文档简介
2016-2017学年陕西省高二(下)期末数学试卷(文科)
一、选择题:(本大题共10小题,每小题4分,满分40分)
1.已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为( )
A.1
B.2
C.3
D.4
2.(1+i)(2+i)=( )
A.1﹣i
B.1+3i
C.3+i
D.3+3i
3.函数y=sin2x+cos2x的最小正周期为( )
A.
B.
C.π
D.2π
4.如图是一个算法流程图,若输入x的值为,则输出的y的值是( )
A.﹣6
B.﹣2
C.2
D.6
5.已知命题p: x∈R,x2﹣x+1≥0.命题q:若a2<b2,则a<b,下列命题为真命题的是( )
A.p∧q
B.p∧¬q
C.¬p∧q
D.¬p∧¬q
6.对具有线性相关关系的变量x、y,有一组观测数据(xi,yi)(i=1,2,3,…,8),其回归方程为y=x+a,且x1+x2+x3+…+x8=6,y1+y2+y3+…+y8=9,则实数a的值是( )
A.﹣2
B.2
C.﹣1
D.1
7.已知奇函数f(x)在R上是增函数.若a=﹣f(),b=f(log24.1),c=f(20.8),则a,b,c的大小关系为( )
A.a<b<c
B.b<a<c
C.c<b<a
D.c<a<b
8.已知F是双曲线C:x2﹣=1的右焦点,P是C上一点,且PF与x轴垂直,点A的坐标是(1,3),则△APF的面积为( )
A.
B.
C.
D.
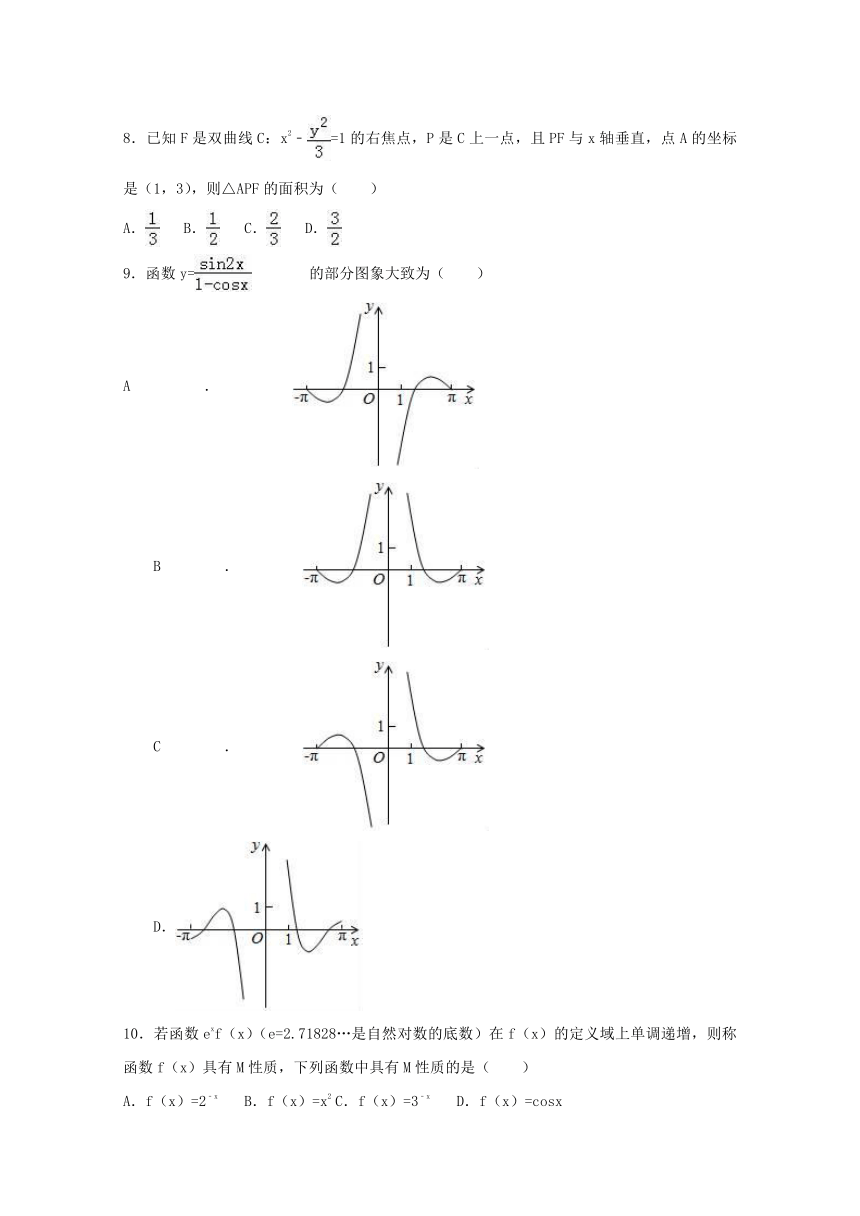
9.函数y=的部分图象大致为( )
A.
B.
C.
D.
10.若函数exf(x)(e=2.71828…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质,下列函数中具有M性质的是( )
A.f(x)=2﹣x
B.f(x)=x2
C.f(x)=3﹣x
D.f(x)=cosx
二、填空题:(本大题共4小题,每小题4分,满分16分)
11.已知,tan
α=2,则cosα=
.
12.曲线y=x2+在点(1,2)处的切线方程为
.
13.△ABC的内角A,B,C的对边分别为a,b,c,若2bcosB=acosC+ccosA,则B=
.
14.已知f(x)是定义在R上的偶函数,且f(x+4)=f(x﹣2).若当x∈时,f(x)=6﹣x,则f(一)必考题:5小题,共54分
15.在△ABC中,角A,B,C的对边分别为a,b,c,已知b=3,
=﹣6,S△ABC=3,求A和a.
16.已知函数f(x)=,
①若f(a)=14,求a的值
②在平面直角坐标系中,作出函数y=f(x)的草图.(需标注函数图象与坐标轴交点处所表示的实数)
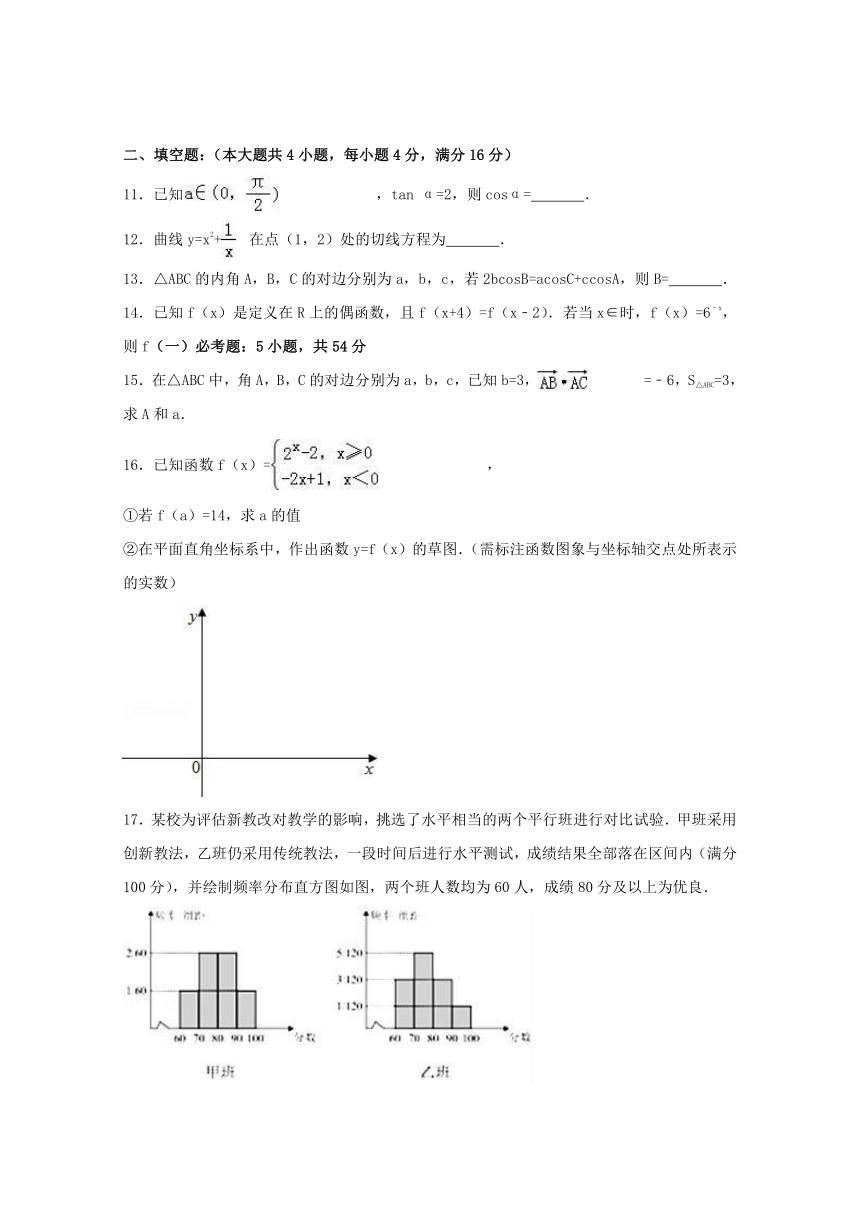
17.某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验.甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在区间内(满分100分),并绘制频率分布直方图如图,两个班人数均为60人,成绩80分及以上为优良.
(1)根据以上信息填好下列2×2联表,并判断出有多大的把握认为学生成绩优良与班级有关?
是否优良班级
优良(人数)
非优良(人数)
合计
甲
乙
合计
(2)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选2人来作书面发言,求2人都来自甲班的概率.
下面的临界值表供参考:
P(x2 k)
0.10
0.05
0.010
k
2.706
3.841
6.635
(以下临界值及公式仅供参考,n=a+b+c+d)
18.已知椭圆C的对称中心为坐标原点O,焦点在x轴上,左右焦点分别为F,F,左右顶点分别为A,B,且|F1F2|=4,|AB|=4
(1)求椭圆的方程;
(2)过F1的直线l与椭圆C相交于M,N两点,若△MF2N的面积为,求直线l的方程.
19.已知函数
f(x)=ex(ex﹣a)﹣a2x.
(1)讨论
f(x)的单调性;
(2)若f(x)≥0,求a的取值范围.
(二)选考题:共10分。请考生在第20、21题中任选一题作答,如果多做,则按所做的第一题计分。
20.在平面直角坐标系中,直线l的参数方程为(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12.
(Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)已知直线l与曲线C交于A,B两点,试求|AB|.
21.已知函数f(x)=|x+1|﹣|x﹣2|.
(1)求不等式f(x)≥1的解集;
(2)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范围.
2016-2017学年陕西省西北大学附中高二(下)期末数学试卷(文科)
参考答案与试题解析
一、选择题:(本大题共10小题,每小题4分,满分40分)
1.已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为( )
A.1
B.2
C.3
D.4
【考点】1E:交集及其运算.
【分析】利用交集定义先求出A∩B,由此能求出A∩B中元素的个数.
【解答】解:∵集合A={1,2,3,4},B={2,4,6,8},
∴A∩B={2,4},
∴A∩B中元素的个数为2.
故选:B.
2.(1+i)(2+i)=( )
A.1﹣i
B.1+3i
C.3+i
D.3+3i
【考点】A5:复数代数形式的乘除运算.
【分析】利用复数的运算法则即可得出.
【解答】解:原式=2﹣1+3i=1+3i.
故选:B.
3.函数y=sin2x+cos2x的最小正周期为( )
A.
B.
C.π
D.2π
【考点】H1:三角函数的周期性及其求法.
【分析】利用辅助角公式,化简函数的解析式,进而根据ω值,可得函数的周期.
【解答】解:∵函数y=sin2x+cos2x=2sin(2x+),
∵ω=2,
∴T=π,
故选:C
4.如图是一个算法流程图,若输入x的值为,则输出的y的值是( )
A.﹣6
B.﹣2
C.2
D.6
【考点】EF:程序框图.
【分析】直接模拟程序的运行即得结论.
【解答】解:初始值x=,不满足x≥1,
所以y=2+log2=2﹣log224=﹣2,
故选:B.
5.已知命题p: x∈R,x2﹣x+1≥0.命题q:若a2<b2,则a<b,下列命题为真命题的是( )
A.p∧q
B.p∧¬q
C.¬p∧q
D.¬p∧¬q
【考点】2K:命题的真假判断与应用;2E:复合命题的真假.
【分析】先判断命题p,q的真假,进而根据复合命题真假的真值表,可得答案.
【解答】解:命题p: x=0∈R,使x2﹣x+1≥0成立.
故命题p为真命题;
当a=1,b=﹣2时,a2<b2成立,但a<b不成立,
故命题q为假命题,
故命题p∧q,¬p∧q,¬p∧¬q均为假命题;
命题p∧¬q为真命题,
故选:B.
6.对具有线性相关关系的变量x、y,有一组观测数据(xi,yi)(i=1,2,3,…,8),其回归方程为y=x+a,且x1+x2+x3+…+x8=6,y1+y2+y3+…+y8=9,则实数a的值是( )
A.﹣2
B.2
C.﹣1
D.1
【考点】BK:线性回归方程.
【分析】求出横坐标和纵坐标的平均数,写出样本中心点,把样本中心点代入线性回归方程,得到关于a的方程,解方程即可.
【解答】解:∵x1+x2+x3+…+x8=6,(y1+y2+y3+…+y8)=9,
∴=,
=,∴样本中心点的坐标为(,),
代入回归直线方程得,
=×+a,∴a=1.
故选:D.
7.已知奇函数f(x)在R上是增函数.若a=﹣f(),b=f(log24.1),c=f(20.8),则a,b,c的大小关系为( )
A.a<b<c
B.b<a<c
C.c<b<a
D.c<a<b
【考点】3N:奇偶性与单调性的综合.
【分析】根据奇函数f(x)在R上是增函数,化简a、b、c,即可得出a,b,c的大小.
【解答】解:奇函数f(x)在R上是增函数,
∴a=﹣f()=f(log25),
b=f(log24.1),
c=f(20.8),
又1<20.8<2<log24.1<log25,
∴f(20.8)<f(log24.1)<f(log25),
即c<b<a.
故选:C.
8.已知F是双曲线C:x2﹣=1的右焦点,P是C上一点,且PF与x轴垂直,点A的坐标是(1,3),则△APF的面积为( )
A.
B.
C.
D.
【考点】KC:双曲线的简单性质.
【分析】由题意求得双曲线的右焦点F(2,0),由PF与x轴垂直,代入即可求得P点坐标,根据三角形的面积公式,即可求得△APF的面积.
【解答】解:由双曲线C:x2﹣=1的右焦点F(2,0),
PF与x轴垂直,设(2,y),y>0,则y=3,
则P(2,3),
∴AP⊥PF,则丨AP丨=1,丨PF丨=3,
∴△APF的面积S=×丨AP丨×丨PF丨=,
同理当y<0时,则△APF的面积S=,
故选D.
9.函数y=的部分图象大致为( )
A.
B.
C.
D.
【考点】3O:函数的图象.
【分析】判断函数的奇偶性排除选项,利用特殊值判断即可.
【解答】解:函数y=,
可知函数是奇函数,排除选项B,
当x=时,f()==,排除A,
x=π时,f(π)=0,排除D.
故选:C.
10.若函数exf(x)(e=2.71828…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质,下列函数中具有M性质的是( )
A.f(x)=2﹣x
B.f(x)=x2
C.f(x)=3﹣x
D.f(x)=cosx
【考点】3F:函数单调性的性质.
【分析】根据已知中函数f(x)具有M性质的定义,可得f(x)=2﹣x时,满足定义.
【解答】解:当f(x)=2﹣x时,函数exf(x)=()x在R上单调递增,函数f(x)具有M性质,
故选:A
二、填空题:(本大题共4小题,每小题4分,满分16分)
11.已知,tan
α=2,则cosα= .
【考点】GI:三角函数的化简求值.
【分析】由题意利用同角三角函数的基本关系、以及三角函数在各个象限中的符号,求得cosα的值.
【解答】解:∵已知,∴sinα>0,cosα>0,
∵tan
α=2=,sin2α+cos2α=1,则cosα=,
故答案为:.
12.曲线y=x2+在点(1,2)处的切线方程为 x﹣y+1=0 .
【考点】6H:利用导数研究曲线上某点切线方程.
【分析】求出函数的导数,求出切线的斜率,利用点斜式求解切线方程即可.
【解答】解:曲线y=x2+,可得y′=2x﹣,
切线的斜率为:k=2﹣1=1.
切线方程为:y﹣2=x﹣1,即:x﹣y+1=0.
故答案为:x﹣y+1=0.
13.△ABC的内角A,B,C的对边分别为a,b,c,若2bcosB=acosC+ccosA,则B= .
【考点】HP:正弦定理;GL:三角函数中的恒等变换应用.
【分析】根据正弦定理和两角和的正弦公式和诱导公式计算即可
【解答】解:∵2bcosB=acosC+ccosA,由正弦定理可得,
2cosBsinB=sinAcosC+sinCcosA=sin(A+C)=sinB,
∵sinB≠0,
∴cosB=,
∵0<B<π,
∴B=,
故答案为:
14.已知f(x)是定义在R上的偶函数,且f(x+4)=f(x﹣2).若当x∈时,f(x)=6﹣x,则f=f(x),函数的周期性可知:f(x)周期为6,则f=f(1),由f(x)为偶函数,则f(1)=f(﹣1),即可求得答案.
【解答】解:由f(x+4)=f(x﹣2).则f(x+6)=f(x),
∴f(x)为周期为6的周期函数,
f=f(1),
由f(x)是定义在R上的偶函数,则f(1)=f(﹣1),
当x∈时,f(x)=6﹣x,
f(﹣1)=6﹣(﹣1)=6,
∴f(一)必考题:5小题,共54分
15.在△ABC中,角A,B,C的对边分别为a,b,c,已知b=3,
=﹣6,S△ABC=3,求A和a.
【考点】9R:平面向量数量积的运算.
【分析】根据向量的数量积和三角形的面积公式可得tanA=﹣1,求出A和c的值,再根据余弦定理即可求出a.
【解答】解:由=﹣6可得bccosA=﹣6,①,
由三角形的面积公式可得S△ABC=bcsinA=3,②
∴tanA=﹣1,
∵0<A<180°,
∴A=135°,
∴c==2,
由余弦定理可得a2=b2+c2﹣2bccosA=9+8+12=29
∴a=
16.已知函数f(x)=,
①若f(a)=14,求a的值
②在平面直角坐标系中,作出函数y=f(x)的草图.(需标注函数图象与坐标轴交点处所表示的实数)
【考点】3O:函数的图象;36:函数解析式的求解及常用方法.
【分析】①分当a≥0时和当a<0时2种情况,分别根据f(a)=14,求得a的值.
②分当x≥0时和当x<0时2种情况,分别作出函数f(x)的图象.
【解答】解:①∵函数f(x)=,f(a)=14,
当a≥0时,由f(a)=2a﹣2=14,求得a=4;
当a<0时,由f(a)=1﹣2a=14,求得a=﹣.
综上可得,a=4或a=﹣.
②当x≥0时,把函数y=2x的图象向下平移2个单位,
可得f(x)的图象;
当x<0时,作出函数y=1﹣2x的图象即可得到f(x)的图象.
在平面直角坐标系中,作出函数y=f(x)的草图,如图所示:
17.某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验.甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在区间内(满分100分),并绘制频率分布直方图如图,两个班人数均为60人,成绩80分及以上为优良.
(1)根据以上信息填好下列2×2联表,并判断出有多大的把握认为学生成绩优良与班级有关?
是否优良班级
优良(人数)
非优良(人数)
合计
甲
乙
合计
(2)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选2人来作书面发言,求2人都来自甲班的概率.
下面的临界值表供参考:
P(x2 k)
0.10
0.05
0.010
k
2.706
3.841
6.635
(以下临界值及公式仅供参考,n=a+b+c+d)
【考点】BL:独立性检验.
【分析】(1)根据所给数据可得列联表,利用公式计算K2的值,对照临界值即可得结论;
(2)利用分层抽样原理与列举法计算基本事件数,求出对应的概率值.
【解答】解:(1)根据题意,填写2×2列联表如下;
是否优良班级
优良(人数)
非优良(人数)
合计
甲
30
30
60
乙
20
40
60
合计
50
70
120
计算,
则有90%的把握认为学生成绩优良与班级有关;
(2)分层抽样甲班抽取了3人,记作a1,a2,a3,乙班抽取了2人,记作b1,b2,
从中任意抽取2人,有{a1,a2},{a1,a3},{a1,b1},{a1,b2},
{a2,a3},{a2,b1},{a2,b2},{a3,b1},{a3,b2},{b1,b2}10种情形,
其中2人都来自甲班的有3种情形,
则至少有2人来自甲班的概率为P=.
18.已知椭圆C的对称中心为坐标原点O,焦点在x轴上,左右焦点分别为F,F,左右顶点分别为A,B,且|F1F2|=4,|AB|=4
(1)求椭圆的方程;
(2)过F1的直线l与椭圆C相交于M,N两点,若△MF2N的面积为,求直线l的方程.
【考点】KL:直线与椭圆的位置关系;K3:椭圆的标准方程.
【分析】(1)由|F1F2|=4,|AB|=4,建立方程组,求出a=2,c=2,b=2,由此能求出椭圆的方程.
(2)由F1(﹣2,0),设过F1的直线l的方程为:x+2=my,由,得(m2+2)y2﹣4my﹣4=0,利用韦达定理、弦长公式、三角形面积公式,能求出m=±1,由此能求出直线l的方程.
【解答】解:(1)∵椭圆C的对称中心为坐标原点O,焦点在x轴上,
左右焦点分别为F,F,左右顶点分别为A,B,且|F1F2|=4,|AB|=4,
∴,解得a=2,c=2,b=2,
∴椭圆的方程为.
(2)由(1)知F1(﹣2,0),设过F1的直线l的方程为:x+2=my,
由,得(m2+2)y2﹣4my﹣4=0,
设M(x1,y1),N(x2,y2),则,
∵△MF2N的面积为,
∴==2=,
化简,得2m4﹣m2﹣1=0,解得m2=1或m2=﹣(舍),
解得m=±1,此时直线l的方程为x﹣y+2=0,或x+y+2=0.
19.已知函数
f(x)=ex(ex﹣a)﹣a2x.
(1)讨论
f(x)的单调性;
(2)若f(x)≥0,求a的取值范围.
【考点】6B:利用导数研究函数的单调性;6K:导数在最大值、最小值问题中的应用.
【分析】(1)先求导,再分类讨论,根据导数和函数的单调性即可判断,
(2)根据(1)的结论,分别求出函数的最小值,即可求出a的范围.
【解答】解:(1)f(x)=ex(ex﹣a)﹣a2x=e2x﹣exa﹣a2x,
∴f′(x)=2e2x﹣aex﹣a2=(2ex+a)(ex﹣a),
①当a=0时,f′(x)>0恒成立,
∴f(x)在R上单调递增,
②当a>0时,2ex+a>0,令f′(x)=0,解得x=lna,
当x<lna时,f′(x)<0,函数f(x)单调递减,
当x>lna时,f′(x)>0,函数f(x)单调递增,
③当a<0时,ex﹣a>0,令f′(x)=0,解得x=ln(﹣),
当x<ln(﹣)时,f′(x)<0,函数f(x)单调递减,
当x>ln(﹣)时,f′(x)>0,函数f(x)单调递增,
综上所述,当a=0时,f(x)在R上单调递增,
当a>0时,f(x)在(﹣∞,lna)上单调递减,在(lna,+∞)上单调递增,
当a<0时,f(x)在(﹣∞,ln(﹣))上单调递减,在(ln(﹣),+∞)上单调递增,
(2)①当a=0时,f(x)=e2x>0恒成立,
②当a>0时,由(1)可得f(x)min=f(lna)=﹣a2lna≥0,
∴lna≤0,
∴0<a≤1,
③当a<0时,由(1)可得f(x)min=f(ln(﹣))=﹣a2ln(﹣)≥0,
∴ln(﹣)≤,
∴﹣2≤a<0,
综上所述a的取值范围为
(二)选考题:共10分。请考生在第20、21题中任选一题作答,如果多做,则按所做的第一题计分。
20.在平面直角坐标系中,直线l的参数方程为(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12.
(Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)已知直线l与曲线C交于A,B两点,试求|AB|.
【考点】Q4:简单曲线的极坐标方程;QH:参数方程化成普通方程.
【分析】(Ⅰ)直接由曲线C的极坐标方程求出曲线C的直角坐标方程即可;
(Ⅱ)把直线l的参数方程代入曲线C的方程得5t2+4t﹣12=0,求出t1+t2和t1t2的值,由此能求出|AB|.
【解答】解:(Ⅰ)∵曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12,
∴曲线C的直角坐标方程为3x2+4y2=12,化简得;
(Ⅱ)把直线l的参数方程代入曲线C的方程,化简整理得5t2+4t﹣12=0,
∴,,
∴|AB|=|t1﹣t2|=.
21.已知函数f(x)=|x+1|﹣|x﹣2|.
(1)求不等式f(x)≥1的解集;
(2)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范围.
【考点】R4:绝对值三角不等式;R5:绝对值不等式的解法.
【分析】(1)由于f(x)=|x+1|﹣|x﹣2|=,解不等式f(x)≥1可分﹣1≤x≤2与x>2两类讨论即可解得不等式f(x)≥1的解集;
(2)依题意可得m≤max,设g(x)=f(x)﹣x2+x,分x≤1、﹣1<x<2、x≥2三类讨论,可求得g(x)max=,从而可得m的取值范围.
【解答】解:(1)∵f(x)=|x+1|﹣|x﹣2|=,f(x)≥1,
∴当﹣1≤x≤2时,2x﹣1≥1,解得1≤x≤2;
当x>2时,3≥1恒成立,故x>2;
综上,不等式f(x)≥1的解集为{x|x≥1}.
(2)原式等价于存在x∈R使得f(x)﹣x2+x≥m成立,
即m≤max,设g(x)=f(x)﹣x2+x.
由(1)知,g(x)=,
当x≤﹣1时,g(x)=﹣x2+x﹣3,其开口向下,对称轴方程为x=>﹣1,
∴g(x)≤g(﹣1)=﹣1﹣1﹣3=﹣5;
当﹣1<x<2时,g(x)=﹣x2+3x﹣1,其开口向下,对称轴方程为x=∈(﹣1,2),
∴g(x)≤g()=﹣+﹣1=;
当x≥2时,g(x)=﹣x2+x+3,其开口向下,对称轴方程为x=<2,
∴g(x)≤g(2)=﹣4+2=3=1;
综上,g(x)max=,
∴m的取值范围为(﹣∞,].
一、选择题:(本大题共10小题,每小题4分,满分40分)
1.已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为( )
A.1
B.2
C.3
D.4
2.(1+i)(2+i)=( )
A.1﹣i
B.1+3i
C.3+i
D.3+3i
3.函数y=sin2x+cos2x的最小正周期为( )
A.
B.
C.π
D.2π
4.如图是一个算法流程图,若输入x的值为,则输出的y的值是( )
A.﹣6
B.﹣2
C.2
D.6
5.已知命题p: x∈R,x2﹣x+1≥0.命题q:若a2<b2,则a<b,下列命题为真命题的是( )
A.p∧q
B.p∧¬q
C.¬p∧q
D.¬p∧¬q
6.对具有线性相关关系的变量x、y,有一组观测数据(xi,yi)(i=1,2,3,…,8),其回归方程为y=x+a,且x1+x2+x3+…+x8=6,y1+y2+y3+…+y8=9,则实数a的值是( )
A.﹣2
B.2
C.﹣1
D.1
7.已知奇函数f(x)在R上是增函数.若a=﹣f(),b=f(log24.1),c=f(20.8),则a,b,c的大小关系为( )
A.a<b<c
B.b<a<c
C.c<b<a
D.c<a<b
8.已知F是双曲线C:x2﹣=1的右焦点,P是C上一点,且PF与x轴垂直,点A的坐标是(1,3),则△APF的面积为( )
A.
B.
C.
D.
9.函数y=的部分图象大致为( )
A.
B.
C.
D.
10.若函数exf(x)(e=2.71828…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质,下列函数中具有M性质的是( )
A.f(x)=2﹣x
B.f(x)=x2
C.f(x)=3﹣x
D.f(x)=cosx
二、填空题:(本大题共4小题,每小题4分,满分16分)
11.已知,tan
α=2,则cosα=
.
12.曲线y=x2+在点(1,2)处的切线方程为
.
13.△ABC的内角A,B,C的对边分别为a,b,c,若2bcosB=acosC+ccosA,则B=
.
14.已知f(x)是定义在R上的偶函数,且f(x+4)=f(x﹣2).若当x∈时,f(x)=6﹣x,则f(一)必考题:5小题,共54分
15.在△ABC中,角A,B,C的对边分别为a,b,c,已知b=3,
=﹣6,S△ABC=3,求A和a.
16.已知函数f(x)=,
①若f(a)=14,求a的值
②在平面直角坐标系中,作出函数y=f(x)的草图.(需标注函数图象与坐标轴交点处所表示的实数)
17.某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验.甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在区间内(满分100分),并绘制频率分布直方图如图,两个班人数均为60人,成绩80分及以上为优良.
(1)根据以上信息填好下列2×2联表,并判断出有多大的把握认为学生成绩优良与班级有关?
是否优良班级
优良(人数)
非优良(人数)
合计
甲
乙
合计
(2)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选2人来作书面发言,求2人都来自甲班的概率.
下面的临界值表供参考:
P(x2 k)
0.10
0.05
0.010
k
2.706
3.841
6.635
(以下临界值及公式仅供参考,n=a+b+c+d)
18.已知椭圆C的对称中心为坐标原点O,焦点在x轴上,左右焦点分别为F,F,左右顶点分别为A,B,且|F1F2|=4,|AB|=4
(1)求椭圆的方程;
(2)过F1的直线l与椭圆C相交于M,N两点,若△MF2N的面积为,求直线l的方程.
19.已知函数
f(x)=ex(ex﹣a)﹣a2x.
(1)讨论
f(x)的单调性;
(2)若f(x)≥0,求a的取值范围.
(二)选考题:共10分。请考生在第20、21题中任选一题作答,如果多做,则按所做的第一题计分。
20.在平面直角坐标系中,直线l的参数方程为(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12.
(Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)已知直线l与曲线C交于A,B两点,试求|AB|.
21.已知函数f(x)=|x+1|﹣|x﹣2|.
(1)求不等式f(x)≥1的解集;
(2)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范围.
2016-2017学年陕西省西北大学附中高二(下)期末数学试卷(文科)
参考答案与试题解析
一、选择题:(本大题共10小题,每小题4分,满分40分)
1.已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为( )
A.1
B.2
C.3
D.4
【考点】1E:交集及其运算.
【分析】利用交集定义先求出A∩B,由此能求出A∩B中元素的个数.
【解答】解:∵集合A={1,2,3,4},B={2,4,6,8},
∴A∩B={2,4},
∴A∩B中元素的个数为2.
故选:B.
2.(1+i)(2+i)=( )
A.1﹣i
B.1+3i
C.3+i
D.3+3i
【考点】A5:复数代数形式的乘除运算.
【分析】利用复数的运算法则即可得出.
【解答】解:原式=2﹣1+3i=1+3i.
故选:B.
3.函数y=sin2x+cos2x的最小正周期为( )
A.
B.
C.π
D.2π
【考点】H1:三角函数的周期性及其求法.
【分析】利用辅助角公式,化简函数的解析式,进而根据ω值,可得函数的周期.
【解答】解:∵函数y=sin2x+cos2x=2sin(2x+),
∵ω=2,
∴T=π,
故选:C
4.如图是一个算法流程图,若输入x的值为,则输出的y的值是( )
A.﹣6
B.﹣2
C.2
D.6
【考点】EF:程序框图.
【分析】直接模拟程序的运行即得结论.
【解答】解:初始值x=,不满足x≥1,
所以y=2+log2=2﹣log224=﹣2,
故选:B.
5.已知命题p: x∈R,x2﹣x+1≥0.命题q:若a2<b2,则a<b,下列命题为真命题的是( )
A.p∧q
B.p∧¬q
C.¬p∧q
D.¬p∧¬q
【考点】2K:命题的真假判断与应用;2E:复合命题的真假.
【分析】先判断命题p,q的真假,进而根据复合命题真假的真值表,可得答案.
【解答】解:命题p: x=0∈R,使x2﹣x+1≥0成立.
故命题p为真命题;
当a=1,b=﹣2时,a2<b2成立,但a<b不成立,
故命题q为假命题,
故命题p∧q,¬p∧q,¬p∧¬q均为假命题;
命题p∧¬q为真命题,
故选:B.
6.对具有线性相关关系的变量x、y,有一组观测数据(xi,yi)(i=1,2,3,…,8),其回归方程为y=x+a,且x1+x2+x3+…+x8=6,y1+y2+y3+…+y8=9,则实数a的值是( )
A.﹣2
B.2
C.﹣1
D.1
【考点】BK:线性回归方程.
【分析】求出横坐标和纵坐标的平均数,写出样本中心点,把样本中心点代入线性回归方程,得到关于a的方程,解方程即可.
【解答】解:∵x1+x2+x3+…+x8=6,(y1+y2+y3+…+y8)=9,
∴=,
=,∴样本中心点的坐标为(,),
代入回归直线方程得,
=×+a,∴a=1.
故选:D.
7.已知奇函数f(x)在R上是增函数.若a=﹣f(),b=f(log24.1),c=f(20.8),则a,b,c的大小关系为( )
A.a<b<c
B.b<a<c
C.c<b<a
D.c<a<b
【考点】3N:奇偶性与单调性的综合.
【分析】根据奇函数f(x)在R上是增函数,化简a、b、c,即可得出a,b,c的大小.
【解答】解:奇函数f(x)在R上是增函数,
∴a=﹣f()=f(log25),
b=f(log24.1),
c=f(20.8),
又1<20.8<2<log24.1<log25,
∴f(20.8)<f(log24.1)<f(log25),
即c<b<a.
故选:C.
8.已知F是双曲线C:x2﹣=1的右焦点,P是C上一点,且PF与x轴垂直,点A的坐标是(1,3),则△APF的面积为( )
A.
B.
C.
D.
【考点】KC:双曲线的简单性质.
【分析】由题意求得双曲线的右焦点F(2,0),由PF与x轴垂直,代入即可求得P点坐标,根据三角形的面积公式,即可求得△APF的面积.
【解答】解:由双曲线C:x2﹣=1的右焦点F(2,0),
PF与x轴垂直,设(2,y),y>0,则y=3,
则P(2,3),
∴AP⊥PF,则丨AP丨=1,丨PF丨=3,
∴△APF的面积S=×丨AP丨×丨PF丨=,
同理当y<0时,则△APF的面积S=,
故选D.
9.函数y=的部分图象大致为( )
A.
B.
C.
D.
【考点】3O:函数的图象.
【分析】判断函数的奇偶性排除选项,利用特殊值判断即可.
【解答】解:函数y=,
可知函数是奇函数,排除选项B,
当x=时,f()==,排除A,
x=π时,f(π)=0,排除D.
故选:C.
10.若函数exf(x)(e=2.71828…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质,下列函数中具有M性质的是( )
A.f(x)=2﹣x
B.f(x)=x2
C.f(x)=3﹣x
D.f(x)=cosx
【考点】3F:函数单调性的性质.
【分析】根据已知中函数f(x)具有M性质的定义,可得f(x)=2﹣x时,满足定义.
【解答】解:当f(x)=2﹣x时,函数exf(x)=()x在R上单调递增,函数f(x)具有M性质,
故选:A
二、填空题:(本大题共4小题,每小题4分,满分16分)
11.已知,tan
α=2,则cosα= .
【考点】GI:三角函数的化简求值.
【分析】由题意利用同角三角函数的基本关系、以及三角函数在各个象限中的符号,求得cosα的值.
【解答】解:∵已知,∴sinα>0,cosα>0,
∵tan
α=2=,sin2α+cos2α=1,则cosα=,
故答案为:.
12.曲线y=x2+在点(1,2)处的切线方程为 x﹣y+1=0 .
【考点】6H:利用导数研究曲线上某点切线方程.
【分析】求出函数的导数,求出切线的斜率,利用点斜式求解切线方程即可.
【解答】解:曲线y=x2+,可得y′=2x﹣,
切线的斜率为:k=2﹣1=1.
切线方程为:y﹣2=x﹣1,即:x﹣y+1=0.
故答案为:x﹣y+1=0.
13.△ABC的内角A,B,C的对边分别为a,b,c,若2bcosB=acosC+ccosA,则B= .
【考点】HP:正弦定理;GL:三角函数中的恒等变换应用.
【分析】根据正弦定理和两角和的正弦公式和诱导公式计算即可
【解答】解:∵2bcosB=acosC+ccosA,由正弦定理可得,
2cosBsinB=sinAcosC+sinCcosA=sin(A+C)=sinB,
∵sinB≠0,
∴cosB=,
∵0<B<π,
∴B=,
故答案为:
14.已知f(x)是定义在R上的偶函数,且f(x+4)=f(x﹣2).若当x∈时,f(x)=6﹣x,则f=f(x),函数的周期性可知:f(x)周期为6,则f=f(1),由f(x)为偶函数,则f(1)=f(﹣1),即可求得答案.
【解答】解:由f(x+4)=f(x﹣2).则f(x+6)=f(x),
∴f(x)为周期为6的周期函数,
f=f(1),
由f(x)是定义在R上的偶函数,则f(1)=f(﹣1),
当x∈时,f(x)=6﹣x,
f(﹣1)=6﹣(﹣1)=6,
∴f(一)必考题:5小题,共54分
15.在△ABC中,角A,B,C的对边分别为a,b,c,已知b=3,
=﹣6,S△ABC=3,求A和a.
【考点】9R:平面向量数量积的运算.
【分析】根据向量的数量积和三角形的面积公式可得tanA=﹣1,求出A和c的值,再根据余弦定理即可求出a.
【解答】解:由=﹣6可得bccosA=﹣6,①,
由三角形的面积公式可得S△ABC=bcsinA=3,②
∴tanA=﹣1,
∵0<A<180°,
∴A=135°,
∴c==2,
由余弦定理可得a2=b2+c2﹣2bccosA=9+8+12=29
∴a=
16.已知函数f(x)=,
①若f(a)=14,求a的值
②在平面直角坐标系中,作出函数y=f(x)的草图.(需标注函数图象与坐标轴交点处所表示的实数)
【考点】3O:函数的图象;36:函数解析式的求解及常用方法.
【分析】①分当a≥0时和当a<0时2种情况,分别根据f(a)=14,求得a的值.
②分当x≥0时和当x<0时2种情况,分别作出函数f(x)的图象.
【解答】解:①∵函数f(x)=,f(a)=14,
当a≥0时,由f(a)=2a﹣2=14,求得a=4;
当a<0时,由f(a)=1﹣2a=14,求得a=﹣.
综上可得,a=4或a=﹣.
②当x≥0时,把函数y=2x的图象向下平移2个单位,
可得f(x)的图象;
当x<0时,作出函数y=1﹣2x的图象即可得到f(x)的图象.
在平面直角坐标系中,作出函数y=f(x)的草图,如图所示:
17.某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验.甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在区间内(满分100分),并绘制频率分布直方图如图,两个班人数均为60人,成绩80分及以上为优良.
(1)根据以上信息填好下列2×2联表,并判断出有多大的把握认为学生成绩优良与班级有关?
是否优良班级
优良(人数)
非优良(人数)
合计
甲
乙
合计
(2)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选2人来作书面发言,求2人都来自甲班的概率.
下面的临界值表供参考:
P(x2 k)
0.10
0.05
0.010
k
2.706
3.841
6.635
(以下临界值及公式仅供参考,n=a+b+c+d)
【考点】BL:独立性检验.
【分析】(1)根据所给数据可得列联表,利用公式计算K2的值,对照临界值即可得结论;
(2)利用分层抽样原理与列举法计算基本事件数,求出对应的概率值.
【解答】解:(1)根据题意,填写2×2列联表如下;
是否优良班级
优良(人数)
非优良(人数)
合计
甲
30
30
60
乙
20
40
60
合计
50
70
120
计算,
则有90%的把握认为学生成绩优良与班级有关;
(2)分层抽样甲班抽取了3人,记作a1,a2,a3,乙班抽取了2人,记作b1,b2,
从中任意抽取2人,有{a1,a2},{a1,a3},{a1,b1},{a1,b2},
{a2,a3},{a2,b1},{a2,b2},{a3,b1},{a3,b2},{b1,b2}10种情形,
其中2人都来自甲班的有3种情形,
则至少有2人来自甲班的概率为P=.
18.已知椭圆C的对称中心为坐标原点O,焦点在x轴上,左右焦点分别为F,F,左右顶点分别为A,B,且|F1F2|=4,|AB|=4
(1)求椭圆的方程;
(2)过F1的直线l与椭圆C相交于M,N两点,若△MF2N的面积为,求直线l的方程.
【考点】KL:直线与椭圆的位置关系;K3:椭圆的标准方程.
【分析】(1)由|F1F2|=4,|AB|=4,建立方程组,求出a=2,c=2,b=2,由此能求出椭圆的方程.
(2)由F1(﹣2,0),设过F1的直线l的方程为:x+2=my,由,得(m2+2)y2﹣4my﹣4=0,利用韦达定理、弦长公式、三角形面积公式,能求出m=±1,由此能求出直线l的方程.
【解答】解:(1)∵椭圆C的对称中心为坐标原点O,焦点在x轴上,
左右焦点分别为F,F,左右顶点分别为A,B,且|F1F2|=4,|AB|=4,
∴,解得a=2,c=2,b=2,
∴椭圆的方程为.
(2)由(1)知F1(﹣2,0),设过F1的直线l的方程为:x+2=my,
由,得(m2+2)y2﹣4my﹣4=0,
设M(x1,y1),N(x2,y2),则,
∵△MF2N的面积为,
∴==2=,
化简,得2m4﹣m2﹣1=0,解得m2=1或m2=﹣(舍),
解得m=±1,此时直线l的方程为x﹣y+2=0,或x+y+2=0.
19.已知函数
f(x)=ex(ex﹣a)﹣a2x.
(1)讨论
f(x)的单调性;
(2)若f(x)≥0,求a的取值范围.
【考点】6B:利用导数研究函数的单调性;6K:导数在最大值、最小值问题中的应用.
【分析】(1)先求导,再分类讨论,根据导数和函数的单调性即可判断,
(2)根据(1)的结论,分别求出函数的最小值,即可求出a的范围.
【解答】解:(1)f(x)=ex(ex﹣a)﹣a2x=e2x﹣exa﹣a2x,
∴f′(x)=2e2x﹣aex﹣a2=(2ex+a)(ex﹣a),
①当a=0时,f′(x)>0恒成立,
∴f(x)在R上单调递增,
②当a>0时,2ex+a>0,令f′(x)=0,解得x=lna,
当x<lna时,f′(x)<0,函数f(x)单调递减,
当x>lna时,f′(x)>0,函数f(x)单调递增,
③当a<0时,ex﹣a>0,令f′(x)=0,解得x=ln(﹣),
当x<ln(﹣)时,f′(x)<0,函数f(x)单调递减,
当x>ln(﹣)时,f′(x)>0,函数f(x)单调递增,
综上所述,当a=0时,f(x)在R上单调递增,
当a>0时,f(x)在(﹣∞,lna)上单调递减,在(lna,+∞)上单调递增,
当a<0时,f(x)在(﹣∞,ln(﹣))上单调递减,在(ln(﹣),+∞)上单调递增,
(2)①当a=0时,f(x)=e2x>0恒成立,
②当a>0时,由(1)可得f(x)min=f(lna)=﹣a2lna≥0,
∴lna≤0,
∴0<a≤1,
③当a<0时,由(1)可得f(x)min=f(ln(﹣))=﹣a2ln(﹣)≥0,
∴ln(﹣)≤,
∴﹣2≤a<0,
综上所述a的取值范围为
(二)选考题:共10分。请考生在第20、21题中任选一题作答,如果多做,则按所做的第一题计分。
20.在平面直角坐标系中,直线l的参数方程为(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12.
(Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)已知直线l与曲线C交于A,B两点,试求|AB|.
【考点】Q4:简单曲线的极坐标方程;QH:参数方程化成普通方程.
【分析】(Ⅰ)直接由曲线C的极坐标方程求出曲线C的直角坐标方程即可;
(Ⅱ)把直线l的参数方程代入曲线C的方程得5t2+4t﹣12=0,求出t1+t2和t1t2的值,由此能求出|AB|.
【解答】解:(Ⅰ)∵曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12,
∴曲线C的直角坐标方程为3x2+4y2=12,化简得;
(Ⅱ)把直线l的参数方程代入曲线C的方程,化简整理得5t2+4t﹣12=0,
∴,,
∴|AB|=|t1﹣t2|=.
21.已知函数f(x)=|x+1|﹣|x﹣2|.
(1)求不等式f(x)≥1的解集;
(2)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范围.
【考点】R4:绝对值三角不等式;R5:绝对值不等式的解法.
【分析】(1)由于f(x)=|x+1|﹣|x﹣2|=,解不等式f(x)≥1可分﹣1≤x≤2与x>2两类讨论即可解得不等式f(x)≥1的解集;
(2)依题意可得m≤max,设g(x)=f(x)﹣x2+x,分x≤1、﹣1<x<2、x≥2三类讨论,可求得g(x)max=,从而可得m的取值范围.
【解答】解:(1)∵f(x)=|x+1|﹣|x﹣2|=,f(x)≥1,
∴当﹣1≤x≤2时,2x﹣1≥1,解得1≤x≤2;
当x>2时,3≥1恒成立,故x>2;
综上,不等式f(x)≥1的解集为{x|x≥1}.
(2)原式等价于存在x∈R使得f(x)﹣x2+x≥m成立,
即m≤max,设g(x)=f(x)﹣x2+x.
由(1)知,g(x)=,
当x≤﹣1时,g(x)=﹣x2+x﹣3,其开口向下,对称轴方程为x=>﹣1,
∴g(x)≤g(﹣1)=﹣1﹣1﹣3=﹣5;
当﹣1<x<2时,g(x)=﹣x2+3x﹣1,其开口向下,对称轴方程为x=∈(﹣1,2),
∴g(x)≤g()=﹣+﹣1=;
当x≥2时,g(x)=﹣x2+x+3,其开口向下,对称轴方程为x=<2,
∴g(x)≤g(2)=﹣4+2=3=1;
综上,g(x)max=,
∴m的取值范围为(﹣∞,].
同课章节目录
