江苏省徐州市2016-2017学年高二数学下学期期末试卷文(含解析)
文档属性
| 名称 | 江苏省徐州市2016-2017学年高二数学下学期期末试卷文(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 289.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-15 22:15:16 | ||
图片预览




文档简介
2016-2017学年江苏省徐州市高二(下)期末数学试卷(文科)
一、填空题:(本大题共14小题,每小题5分,共70分)
1.已知集合A={1,a},B={1,3},若A∪B={1,2,3},则实数A的值为
.
2.已知复数z=i(3﹣i),其中i是虚数单位,则复数z的实部是
..
3.计算:sin210°的值为
.
4.函数y=3x﹣x3的单调递增区间为
.
5.已知复数z=,其中i是虚数单位,则z的模是
.
6.不等式4x>2的解集为
.
7.用反证法证明“a,b∈N
,若ab是偶数,则a,b中至少有一个是偶数”时,应假设
.
8.已知tabα=2,则tan(α﹣)的值为
.
9.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<)的部分图象如图所示,则f(0)的值为
.
10.已知函数f(x)=+sinx,求f(﹣2)+f(﹣1)+f(0)+f(1)+f(2)的值.
11.已知函数f(x)=x2﹣cosx,x∈,则满足f(x0)>f()的x0的取值范围为
.
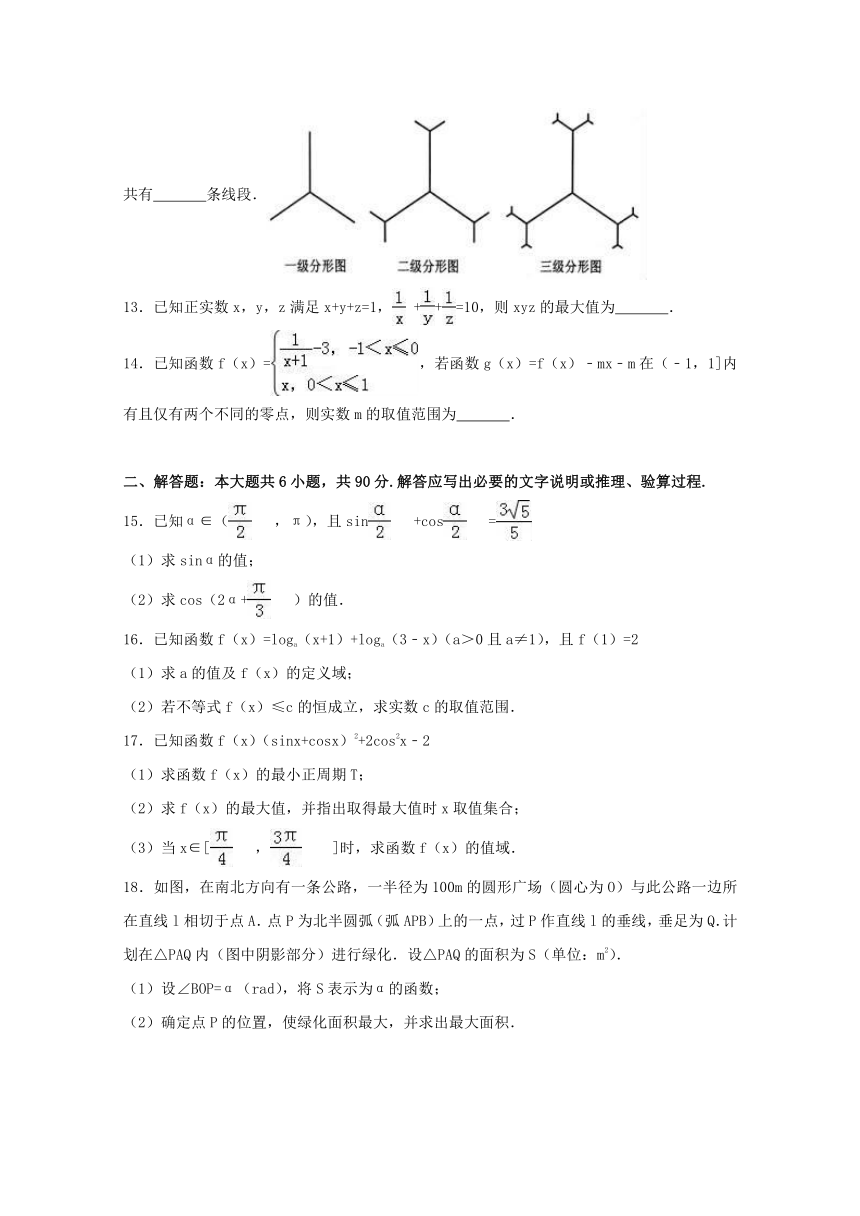
12.某种平面分形如图所示,以及分形图是有一点出发的三条线段,二级分形图是在一级分形图的每条线段的末端出发在生成两条线段,…,依次规律得到n级分形图,那么n级分形图中共有
条线段.
13.已知正实数x,y,z满足x+y+z=1,
++=10,则xyz的最大值为
.
14.已知函数f(x)=,若函数g(x)=f(x)﹣mx﹣m在(﹣1,1]内有且仅有两个不同的零点,则实数m的取值范围为
.
二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程.
15.已知α∈(,π),且sin+cos=
(1)求sinα的值;
(2)求cos(2α+)的值.
16.已知函数f(x)=loga(x+1)+loga(3﹣x)(a>0且a≠1),且f(1)=2
(1)求a的值及f(x)的定义域;
(2)若不等式f(x)≤c的恒成立,求实数c的取值范围.
17.已知函数f(x)(sinx+cosx)2+2cos2x﹣2
(1)求函数f(x)的最小正周期T;
(2)求f(x)的最大值,并指出取得最大值时x取值集合;
(3)当x∈[,]时,求函数f(x)的值域.
18.如图,在南北方向有一条公路,一半径为100m的圆形广场(圆心为O)与此公路一边所在直线l相切于点A.点P为北半圆弧(弧APB)上的一点,过P作直线l的垂线,垂足为Q.计划在△PAQ内(图中阴影部分)进行绿化.设△PAQ的面积为S(单位:m2).
(1)设∠BOP=α(rad),将S表示为α的函数;
(2)确定点P的位置,使绿化面积最大,并求出最大面积.
19.已知函数f(x)=ax3+bx2﹣3x(a,b∈R)在点(1,f(1))处的切线方程为y+2=0.
(1)求函数f(x)的解析式;
(2)若对于区间上任意两个自变量的值x1,x2都有|f(x1)﹣f(x2)|≤c,求实数c的最小值;
(3)若过点M(2,m)(m≠2)可作曲线y=f(x)的三条切线,求实数m的取值范围.
20.已知函数f(x)=xlnx﹣x2﹣x+a,a∈R
(1)当a=0时,求函数f(x)的极值;
(2)若函数f(x)在其定义域内有两个不同的极值点(极值点是指函数取极值时对应的自变量的值),记为x1,x2,且x1<x2.
(ⅰ)求a的取值范围;
(ⅱ)若不等式e1+λ<x1 x恒成立,求正实数λ的取值范围.
2016-2017学年江苏省徐州市高二(下)期末数学试卷(文科)
参考答案与试题解析
一、填空题:(本大题共14小题,每小题5分,共70分)
1.已知集合A={1,a},B={1,3},若A∪B={1,2,3},则实数A的值为 2 .
【考点】1D:并集及其运算.
【分析】利用并集的性质求解.
【解答】解:∵集合A={1,a},B={1,3},若A∪B={1,2,3},
∴a=2.
故答案为:2.
2.已知复数z=i(3﹣i),其中i是虚数单位,则复数z的实部是 1 ..
【考点】A5:复数代数形式的乘除运算.
【分析】利用复数代数形式的乘法运算化简得答案.
【解答】解:∵z=i(3﹣i)=﹣i2+3i=1+3i,
∴复数z的实部是1.
故答案为:1.
3.计算:sin210°的值为 ﹣ .
【考点】GN:诱导公式的作用.
【分析】利用诱导公式可得sin210°=sin=﹣sin30°,由此求得结果.
【解答】解:sin210°=sin=﹣sin30°=﹣,
故答案为﹣.
4.函数y=3x﹣x3的单调递增区间为 .
【考点】6B:利用导数研究函数的单调性.
【分析】先求函数导数,令导数大于等于0,解得x的范围就是函数的单调增区间.
【解答】解:对函数y=3x﹣x3求导,得,y′=3﹣3x2,
令y′≥0,即3﹣3x2≥0,解得,﹣1≤x≤1,
∴函数y=3x﹣x3的递增区间为,
故答案为:.
5.已知复数z=,其中i是虚数单位,则z的模是 .
【考点】A5:复数代数形式的乘除运算.
【分析】利用复数代数形式的乘除运算化简,再由复数模的计算公式求解.
【解答】解:∵z==,
∴|z|=.
故答案为:.
6.不等式4x>2的解集为 {x|﹣1<x<3} .
【考点】7J:指、对数不等式的解法.
【分析】根据指数函数的性质得到一元二次不等式,解出即可.
【解答】解:∵4x>2,
∴2x>x2﹣3,即x2﹣2x﹣3<0,
解得:﹣1<x<3,
故答案为:{x|﹣1<x<3}.
7.用反证法证明“a,b∈N
,若ab是偶数,则a,b中至少有一个是偶数”时,应假设 a,b都不是偶数 .
【考点】R9:反证法与放缩法.
【分析】找出题中的题设,然后根据反证法的定义对其进行否定.
【解答】解:∵命题“a b(a,b∈Z
)为偶数,那么a,b中至少有一个是偶数.”
可得题设为,“a b(a,b∈Z
)为偶数,
∴反设的内容是:假设a,b都为奇数(a,b都不是偶数),
故答案为:a,b都不是偶数
8.已知tabα=2,则tan(α﹣)的值为 .
【考点】GR:两角和与差的正切函数.
【分析】直接利用两角差的正确化简求值.
【解答】解:由tanα=2,
得tan(α﹣)=.
故答案为:.
9.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<)的部分图象如图所示,则f(0)的值为 .
【考点】HK:由y=Asin(ωx+φ)的部分图象确定其解析式.
【分析】由函数f(x)的部分图象,得出A、T、ω与φ的值,
写出f(x)的解析式,计算f(0)的值.
【解答】解:由函数f(x)=Asin(ωx+φ)的部分图象知,
A=2,
=﹣(﹣)=,∴T=;
又T==,∴ω=;
当x=时,f(x)=2,
由五点法画图知,ωx+φ=,
即×+φ=,
解得φ=;
∴f(x)=2sin(x+),
∴f(0)=2sin=.
故答案为:.
10.已知函数f(x)=+sinx,求f(﹣2)+f(﹣1)+f(0)+f(1)+f(2)的值.
【考点】3T:函数的值.
【分析】根据条件求出函数f(x)+f(﹣x)=2,进行求解即可.
【解答】解:∵f(x)+f(﹣x)=,且f(0)=1,
∴f(﹣2)+f(﹣1)+f(0)+f(1)+f(2)=5.
11.已知函数f(x)=x2﹣cosx,x∈,则满足f(x0)>f()的x0的取值范围为 .
【考点】6B:利用导数研究函数的单调性.
【分析】先充分考虑函数f(x)=x2﹣cosx,x∈的性质,为偶函数,其图象关于y轴对称,故考虑函数区间上的情形,利用导数可得函数在单调递增,再结合f(x0)>f()和对称性即可得x0的取值范围.
【解答】解:注意到函数f(x)=x2﹣cosx,x∈是偶函数,
故只需考虑区间上的情形.
当x∈时,f′(x)=2x+sinx≥0,
∴函数在单调递增,
所以f(x0)>f()在上的解集为(,],
结合函数是偶函数,图象关于y轴对称,
得原问题中x0取值范围是,
故答案为:.
12.某种平面分形如图所示,以及分形图是有一点出发的三条线段,二级分形图是在一级分形图的每条线段的末端出发在生成两条线段,…,依次规律得到n级分形图,那么n级分形图中共有 3 2n﹣3 条线段.
【考点】F1:归纳推理.
【分析】n级分形图中的线段条数是以3为首项,2为公比的等比数列的和;
【解答】解:n级分形图中的线段条数是以3为首项,2为公比的等比数列的和,即=3 2n﹣3;
故答案为:3 2n﹣3
13.已知正实数x,y,z满足x+y+z=1,
++=10,则xyz的最大值为 .
【考点】RI:平均值不等式.
【分析】又条件可得z=1﹣(x+y),设xy=a,x+y=b,则xyz=,设f(b)=,利用导数判断f(b)的单调性,计算极值,根据b的范围得出f(b)的最大值.
【解答】解:∵x+y+z=1,∴z=1﹣(x+y),
∴,
即=10,
设xy=a,x+y=b,则0<a<1,0<b<1,
∴,化简得a=.
∴xyz=xy=a(1﹣b)=(1﹣b) =.
令f(b)=,则f′(b)=,
令f′(b)=0得﹣20b3+47b2﹣36b+9=0,即(4b﹣3)(5b﹣3)(1﹣b)=0,
解得b=或b=或b=1(舍),
∴当0<b<或时,f′(b)>0,
当时,f′(b)<0,
∴f(b)在(0,)上单调递增,在(,)上单调递减,在(,1)上单调递增,
∴当b=时,f(b)取得极大值f()=.
又f(1)=0,
∴f(b)的最大值为.
故答案为.
14.已知函数f(x)=,若函数g(x)=f(x)﹣mx﹣m在(﹣1,1]内有且仅有两个不同的零点,则实数m的取值范围为 (,﹣2]∪(0,] .
【考点】52:函数零点的判定定理.
【分析】由g(x)=f(x)﹣mx﹣m=0,即f(x)=m(x+1),作出两个函数的图象,利用数形结合即可得到结论.
【解答】解:由g(x)=f(x)﹣mx﹣m=0,即f(x)=m(x+1),
分别作出函数f(x)和y=h(x)=m(x+1)的图象如图:
由图象可知f(1)=1,h(x)表示过定点A(﹣1,0)的直线,
当h(x)过(1,1)时,m=,此时两个函数有两个交点,
此时满足条件的m的取值范围是0<m≤,
当h(x)过(0,﹣2)时,h(0)=﹣2,解得m=﹣2,此时两个函数有两个交点,
当h(x)与f(x)相切时,两个函数只有一个交点,此时x﹣3=m(x+1)即m(x+1)2+3(x+1)﹣1=0,
当m=0时,只有1解,当m≠0,由△=9+4m=0得m=﹣,此时直线和f(x)相切,
∴要使函数有两个零点,则﹣<m≤﹣2或0<m≤.
故答案为:(,﹣2]∪(0,].
二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程.
15.已知α∈(,π),且sin+cos=
(1)求sinα的值;
(2)求cos(2α+)的值.
【考点】GI:三角函数的化简求值.
【分析】(1)由sin+cos=两边平方化简整理即可得sinα的值;
(2)由α∈(,π)和sinα的值,即可求出cosα,再由二倍角公式求出sin2α和cos2α,再由两角和的余弦公式计算得答案.
【解答】解:(1)∵sin+cos=,
∴(sin+cos)2=,即.
∴.
∴sinα=;
(2)∵α∈(,π),sinα=,
∴.
∴sin2α=2sinαcosα=,
.
∴cos(2α+)==.
16.已知函数f(x)=loga(x+1)+loga(3﹣x)(a>0且a≠1),且f(1)=2
(1)求a的值及f(x)的定义域;
(2)若不等式f(x)≤c的恒成立,求实数c的取值范围.
【考点】4H:对数的运算性质.
【分析】(1)由f(1)=loga2+loga2=2,解得a=2.可得f(x)=log2(x+1)+log2(3﹣x),由,可得函数f(x)的定义域.
(2)由(1)可知:f(x)=log2(x+1)+log2(3﹣x)=log2(x+1)(3﹣x)=,利用二次函数与对数函数的单调性即可得出.
【解答】解:(1)∵f(1)=loga2+loga2=2,解得a=2.
∴f(x)=log2(x+1)+log2(3﹣x),
由,解得﹣1<x<3,
可得函数f(x)的定义域为:(﹣1,3).
(2)由(1)可知:f(x)=log2(x+1)+log2(3﹣x)=log2(x+1)(3﹣x)==,
可知:当x=1时,函数f(x)取得最大值,f(1)=log24=2.
由不等式f(x)≤c的恒成立,∴c≥2.
∴实数c的取值范围是时,求函数f(x)的值域.
【考点】GL:三角函数中的恒等变换应用.
【分析】(1)利用二倍角和辅助角公式化简为y=Asin(ωx+φ)的形式,再利用周期公式求函数的最小正周期;
(2)根据三角函数的性质即可得f(x)的最大值,以及取得最大值时x取值集合;
(3)当x∈[,]时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的最大值和最小值,即得到f(x)的值域.
【解答】解:函数f(x)=(sinx+cosx)2+2cos2x﹣2
化简可得:f(x)=1+2sinxcosx+1+cos2x﹣2=sin2x+cos2x=sin(2x+)
(1)函数f(x)的最小正周期T=.
(2)令2x+=,k∈Z,
得:x=.
∴当x=时,f(x)取得最大值为.
∴取得最大值时x取值集合为{x|x=,k∈Z}.
(3)当x∈[,]时,
可得:2x+∈[,],
∴﹣1≤sin(2x+)≤
∴≤sin(2x+)≤1.
故得当x∈[,]时,函数f(x)的值域为[,1].
18.如图,在南北方向有一条公路,一半径为100m的圆形广场(圆心为O)与此公路一边所在直线l相切于点A.点P为北半圆弧(弧APB)上的一点,过P作直线l的垂线,垂足为Q.计划在△PAQ内(图中阴影部分)进行绿化.设△PAQ的面积为S(单位:m2).
(1)设∠BOP=α(rad),将S表示为α的函数;
(2)确定点P的位置,使绿化面积最大,并求出最大面积.
【考点】HN:在实际问题中建立三角函数模型;6E:利用导数求闭区间上函数的最值.
【分析】(1)若∠BOP=α,则P点坐标(x,y)中,x=AQ=100sinα,y=PQ=100+100cosα,α∈(0,π),根据三角形面积公式,我们易将S表示为α的函数.
(2)由(1)中结论,我们可利用导数法,判断函数的单调性,进而求出函数的最大值,即最大绿化面积.
【解答】解:(1)AQ=100sinα,PQ=100+100cosα,α∈(0,π),
则△PAQ的面积
=5000(sinα+sinαcosα),(0<α<π).
(2)S/=5000(cosα+cos2α﹣sin2α)
=5000(2cos2α+cosα﹣1)
=5000(2cosα﹣1)(cosα+1),
令,cosα=﹣1(舍去),此时.
当关于α为增函数;
当关于α为减函数.
∴当时,(m2),此时PQ=150m.
答:当点P距公路边界l为150m时,绿化面积最大,
19.已知函数f(x)=ax3+bx2﹣3x(a,b∈R)在点(1,f(1))处的切线方程为y+2=0.
(1)求函数f(x)的解析式;
(2)若对于区间上任意两个自变量的值x1,x2都有|f(x1)﹣f(x2)|≤c,求实数c的最小值;
(3)若过点M(2,m)(m≠2)可作曲线y=f(x)的三条切线,求实数m的取值范围.
【考点】6D:利用导数研究函数的极值;36:函数解析式的求解及常用方法;6H:利用导数研究曲线上某点切线方程.
【分析】(1)由题意,利用导函数的几何含义及切点的实质建立a,b的方程,然后求解即可;
(2)由题意,对于定义域内任意自变量都使得|f(x1)﹣f(x2)|≤c,可以转化为求函数在定义域下的最值即可得解;
(3)由题意,若过点M(2,m)(m≠2)可作曲线y=f(x)的三条切线,等价与函数在切点处导函数值等于切线的斜率这一方程有3解.
【解答】解:(1)f'(x)=3ax2+2bx﹣3.
根据题意,得即解得
所以f(x)=x3﹣3x.
(2)令f'(x)=0,即3x2﹣3=0.得x=±1.
当x∈(﹣∞,﹣1)时,f′(x)>0,函数f(x)在此区间单调递增;
当x∈(﹣1,1)时,f′(x)<0,函数f(x)在此区间单调递减
因为f(﹣1)=2,f(1)=﹣2,
所以当x∈时,f(x)max=2,f(x)min=﹣2.
则对于区间上任意两个自变量的值x1,x2,都有|f(x1)﹣f(x2)|≤|f(x)max﹣f(x)min|=4,所以c≥4.
所以c的最小值为4.
(3)因为点M(2,m)(m≠2)不在曲线y=f(x)上,所以可设切点为(x0,y0).
则y0=x03﹣3x0.
因为f'(x0)=3x02﹣3,所以切线的斜率为3x02﹣3.
则3x02﹣3=,
即2x03﹣6x02+6+m=0.
因为过点M(2,m)(m≠2)可作曲线y=f(x)的三条切线,
所以方程2x03﹣6x02+6+m=0有三个不同的实数解.
所以函数g(x)=2x3﹣6x2+6+m有三个不同的零点.
则g'(x)=6x2﹣12x.令g'(x)=0,则x=0或x=2.
当x∈(﹣∞,0)时,g′(x)>0,函数g(x)在此区间单调递增;当x∈(0,2)时,g′(x)<0,函数g(x)在此区间单调递减;
所以,函数g(x)在x=0处取极大值,在x=2处取极小值,有方程与函数的关系知要满足题意必须满足:
,即,解得﹣6<m<2.
20.已知函数f(x)=xlnx﹣x2﹣x+a,a∈R
(1)当a=0时,求函数f(x)的极值;
(2)若函数f(x)在其定义域内有两个不同的极值点(极值点是指函数取极值时对应的自变量的值),记为x1,x2,且x1<x2.
(ⅰ)求a的取值范围;
(ⅱ)若不等式e1+λ<x1 x恒成立,求正实数λ的取值范围.
【考点】6D:利用导数研究函数的极值;6B:利用导数研究函数的单调性.
【分析】(1)求出f(x)的解析式,求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极小值即可;
(2)(i)由导数与极值的关系知可转化为方程f′(x)=lnx﹣ax=0在(0,+∞)有两个不同根;再转化为函数y=lnx与函数y=ax的图象在(0,+∞)上有两个不同交点,或转化为函数g(x)=与函数y=a的图象在(0,+∞)上有两个不同交点;或转化为g(x)=lnx﹣ax有两个不同零点,从而讨论求解;
(ii)e1+λ<x1 x2λ可化为1+λ<lnx1+λlnx2,结合方程的根知1+λ<ax1+λax2=a(x1+λx2),从而可得a>;而a=,从而可得ln
<恒成立;再令t=,t∈(0,1),从而可得不等式lnt<在t∈(0,1)上恒成立,再令h(t)=lnt﹣,从而利用导数化恒成立问题为最值问题即可.
【解答】解:(1)a=0时,f(x)=xlnx﹣x,函数的定义域是(0,+∞),
f(x)=lnx,令f′(x)>0,解得:x>1,令f′(x)<0,解得:0<x<1,
故函数在(0,1)递减,在(1,+∞)递增,
故函数的极小值是f(1)=﹣1;
(2)(i)由题意知,函数f(x)的定义域为(0,+∞),
方程f′(x)=0在(0,+∞)有两个不同根;
即方程lnx﹣ax=0在(0,+∞)有两个不同根;
(解法一)转化为函数y=lnx与函数y=ax的图象在(0,+∞)上有两个不同交点,
如右图.
可见,若令过原点且切于函数y=lnx图象的直线斜率为k,只须0<a<k.
令切点A(x0,lnx0),
故k=y′|x=x0=,又k=,
故=,解得,x0=e,
故k=,故0<a<.
(解法二)转化为函数g(x)=与函数y=a的图象在(0,+∞)上有两个不同交点
又g′(x)=,
即0<x<e时,g′(x)>0,x>e时,g′(x)<0,
故g(x)在(0,e)上单调增,在(e,+∞)上单调减.
故g(x)极大=g(e)=;
又g(x)有且只有一个零点是1,且在x→0时,g(x)→﹣∞,在在x→+∞时,g(x)→0,
故g(x)的草图如右图,
可见,要想函数g(x)=与函数y=a的图象在(0,+∞)上有两个不同交点,
只须0<a<.
(解法三)令g(x)=lnx﹣ax,从而转化为函数g(x)有两个不同零点,
而g′(x)=﹣ax=(x>0),
若a≤0,可见g′(x)>0在(0,+∞)上恒成立,所以g(x)在(0,+∞)单调增,
此时g(x)不可能有两个不同零点.
若a>0,在0<x<时,g′(x)>0,在x>时,g′(x)<0,
所以g(x)在(0,)上单调增,在(,+∞)上单调减,从而g(x)极大值=g()=ln﹣1,
又因为在x→0时,g(x)→﹣∞,在在x→+∞时,g(x)→﹣∞,
于是只须:g(x)极大>0,即ln﹣1>0,所以0<a<.
综上所述,0<a<.
(ii)因为e1+λ<x1 x2λ等价于1+λ<lnx1+λlnx2.
由(i)可知x1,x2分别是方程lnx﹣ax=0的两个根,
即lnx1=ax1,lnx2=ax2
所以原式等价于1+λ<ax1+λax2=a(x1+λx2),因为λ>0,0<x1<x2,
所以原式等价于a>,
又由lnx1=ax1,lnx2=ax2作差得,ln
=a(x1﹣x2),
即a=,所以原式等价于>,
因为0<x1<x2,原式恒成立,即ln<恒成立,
令t=,t∈(0,1),
则不等式lnt<在t∈(0,1)上恒成立.
令h(t)=lnt﹣,
又h′(t)=,
当λ2≥1时,可见t∈(0,1)时,h′(t)>0,
所以h(t)在t∈(0,1)上单调增,又h(1)=0,h(t)<0在t∈(0,1)恒成立,符合题意.
当λ2<1时,可见t∈(0,λ2)时,h′(t)>0,t∈(λ2,1)时h′(t)<0,
所以h(t)在t∈(0,λ2)时单调增,在t∈(λ2,1)时单调减,又h(1)=0,
所以h(t)在t∈(0,1)上不能恒小于0,不符合题意,舍去.
综上所述,若不等式e1+λ<x1 x2λ恒成立,只须λ2≥1,又λ>0,所以λ≥1.
一、填空题:(本大题共14小题,每小题5分,共70分)
1.已知集合A={1,a},B={1,3},若A∪B={1,2,3},则实数A的值为
.
2.已知复数z=i(3﹣i),其中i是虚数单位,则复数z的实部是
..
3.计算:sin210°的值为
.
4.函数y=3x﹣x3的单调递增区间为
.
5.已知复数z=,其中i是虚数单位,则z的模是
.
6.不等式4x>2的解集为
.
7.用反证法证明“a,b∈N
,若ab是偶数,则a,b中至少有一个是偶数”时,应假设
.
8.已知tabα=2,则tan(α﹣)的值为
.
9.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<)的部分图象如图所示,则f(0)的值为
.
10.已知函数f(x)=+sinx,求f(﹣2)+f(﹣1)+f(0)+f(1)+f(2)的值.
11.已知函数f(x)=x2﹣cosx,x∈,则满足f(x0)>f()的x0的取值范围为
.
12.某种平面分形如图所示,以及分形图是有一点出发的三条线段,二级分形图是在一级分形图的每条线段的末端出发在生成两条线段,…,依次规律得到n级分形图,那么n级分形图中共有
条线段.
13.已知正实数x,y,z满足x+y+z=1,
++=10,则xyz的最大值为
.
14.已知函数f(x)=,若函数g(x)=f(x)﹣mx﹣m在(﹣1,1]内有且仅有两个不同的零点,则实数m的取值范围为
.
二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程.
15.已知α∈(,π),且sin+cos=
(1)求sinα的值;
(2)求cos(2α+)的值.
16.已知函数f(x)=loga(x+1)+loga(3﹣x)(a>0且a≠1),且f(1)=2
(1)求a的值及f(x)的定义域;
(2)若不等式f(x)≤c的恒成立,求实数c的取值范围.
17.已知函数f(x)(sinx+cosx)2+2cos2x﹣2
(1)求函数f(x)的最小正周期T;
(2)求f(x)的最大值,并指出取得最大值时x取值集合;
(3)当x∈[,]时,求函数f(x)的值域.
18.如图,在南北方向有一条公路,一半径为100m的圆形广场(圆心为O)与此公路一边所在直线l相切于点A.点P为北半圆弧(弧APB)上的一点,过P作直线l的垂线,垂足为Q.计划在△PAQ内(图中阴影部分)进行绿化.设△PAQ的面积为S(单位:m2).
(1)设∠BOP=α(rad),将S表示为α的函数;
(2)确定点P的位置,使绿化面积最大,并求出最大面积.
19.已知函数f(x)=ax3+bx2﹣3x(a,b∈R)在点(1,f(1))处的切线方程为y+2=0.
(1)求函数f(x)的解析式;
(2)若对于区间上任意两个自变量的值x1,x2都有|f(x1)﹣f(x2)|≤c,求实数c的最小值;
(3)若过点M(2,m)(m≠2)可作曲线y=f(x)的三条切线,求实数m的取值范围.
20.已知函数f(x)=xlnx﹣x2﹣x+a,a∈R
(1)当a=0时,求函数f(x)的极值;
(2)若函数f(x)在其定义域内有两个不同的极值点(极值点是指函数取极值时对应的自变量的值),记为x1,x2,且x1<x2.
(ⅰ)求a的取值范围;
(ⅱ)若不等式e1+λ<x1 x恒成立,求正实数λ的取值范围.
2016-2017学年江苏省徐州市高二(下)期末数学试卷(文科)
参考答案与试题解析
一、填空题:(本大题共14小题,每小题5分,共70分)
1.已知集合A={1,a},B={1,3},若A∪B={1,2,3},则实数A的值为 2 .
【考点】1D:并集及其运算.
【分析】利用并集的性质求解.
【解答】解:∵集合A={1,a},B={1,3},若A∪B={1,2,3},
∴a=2.
故答案为:2.
2.已知复数z=i(3﹣i),其中i是虚数单位,则复数z的实部是 1 ..
【考点】A5:复数代数形式的乘除运算.
【分析】利用复数代数形式的乘法运算化简得答案.
【解答】解:∵z=i(3﹣i)=﹣i2+3i=1+3i,
∴复数z的实部是1.
故答案为:1.
3.计算:sin210°的值为 ﹣ .
【考点】GN:诱导公式的作用.
【分析】利用诱导公式可得sin210°=sin=﹣sin30°,由此求得结果.
【解答】解:sin210°=sin=﹣sin30°=﹣,
故答案为﹣.
4.函数y=3x﹣x3的单调递增区间为 .
【考点】6B:利用导数研究函数的单调性.
【分析】先求函数导数,令导数大于等于0,解得x的范围就是函数的单调增区间.
【解答】解:对函数y=3x﹣x3求导,得,y′=3﹣3x2,
令y′≥0,即3﹣3x2≥0,解得,﹣1≤x≤1,
∴函数y=3x﹣x3的递增区间为,
故答案为:.
5.已知复数z=,其中i是虚数单位,则z的模是 .
【考点】A5:复数代数形式的乘除运算.
【分析】利用复数代数形式的乘除运算化简,再由复数模的计算公式求解.
【解答】解:∵z==,
∴|z|=.
故答案为:.
6.不等式4x>2的解集为 {x|﹣1<x<3} .
【考点】7J:指、对数不等式的解法.
【分析】根据指数函数的性质得到一元二次不等式,解出即可.
【解答】解:∵4x>2,
∴2x>x2﹣3,即x2﹣2x﹣3<0,
解得:﹣1<x<3,
故答案为:{x|﹣1<x<3}.
7.用反证法证明“a,b∈N
,若ab是偶数,则a,b中至少有一个是偶数”时,应假设 a,b都不是偶数 .
【考点】R9:反证法与放缩法.
【分析】找出题中的题设,然后根据反证法的定义对其进行否定.
【解答】解:∵命题“a b(a,b∈Z
)为偶数,那么a,b中至少有一个是偶数.”
可得题设为,“a b(a,b∈Z
)为偶数,
∴反设的内容是:假设a,b都为奇数(a,b都不是偶数),
故答案为:a,b都不是偶数
8.已知tabα=2,则tan(α﹣)的值为 .
【考点】GR:两角和与差的正切函数.
【分析】直接利用两角差的正确化简求值.
【解答】解:由tanα=2,
得tan(α﹣)=.
故答案为:.
9.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<)的部分图象如图所示,则f(0)的值为 .
【考点】HK:由y=Asin(ωx+φ)的部分图象确定其解析式.
【分析】由函数f(x)的部分图象,得出A、T、ω与φ的值,
写出f(x)的解析式,计算f(0)的值.
【解答】解:由函数f(x)=Asin(ωx+φ)的部分图象知,
A=2,
=﹣(﹣)=,∴T=;
又T==,∴ω=;
当x=时,f(x)=2,
由五点法画图知,ωx+φ=,
即×+φ=,
解得φ=;
∴f(x)=2sin(x+),
∴f(0)=2sin=.
故答案为:.
10.已知函数f(x)=+sinx,求f(﹣2)+f(﹣1)+f(0)+f(1)+f(2)的值.
【考点】3T:函数的值.
【分析】根据条件求出函数f(x)+f(﹣x)=2,进行求解即可.
【解答】解:∵f(x)+f(﹣x)=,且f(0)=1,
∴f(﹣2)+f(﹣1)+f(0)+f(1)+f(2)=5.
11.已知函数f(x)=x2﹣cosx,x∈,则满足f(x0)>f()的x0的取值范围为 .
【考点】6B:利用导数研究函数的单调性.
【分析】先充分考虑函数f(x)=x2﹣cosx,x∈的性质,为偶函数,其图象关于y轴对称,故考虑函数区间上的情形,利用导数可得函数在单调递增,再结合f(x0)>f()和对称性即可得x0的取值范围.
【解答】解:注意到函数f(x)=x2﹣cosx,x∈是偶函数,
故只需考虑区间上的情形.
当x∈时,f′(x)=2x+sinx≥0,
∴函数在单调递增,
所以f(x0)>f()在上的解集为(,],
结合函数是偶函数,图象关于y轴对称,
得原问题中x0取值范围是,
故答案为:.
12.某种平面分形如图所示,以及分形图是有一点出发的三条线段,二级分形图是在一级分形图的每条线段的末端出发在生成两条线段,…,依次规律得到n级分形图,那么n级分形图中共有 3 2n﹣3 条线段.
【考点】F1:归纳推理.
【分析】n级分形图中的线段条数是以3为首项,2为公比的等比数列的和;
【解答】解:n级分形图中的线段条数是以3为首项,2为公比的等比数列的和,即=3 2n﹣3;
故答案为:3 2n﹣3
13.已知正实数x,y,z满足x+y+z=1,
++=10,则xyz的最大值为 .
【考点】RI:平均值不等式.
【分析】又条件可得z=1﹣(x+y),设xy=a,x+y=b,则xyz=,设f(b)=,利用导数判断f(b)的单调性,计算极值,根据b的范围得出f(b)的最大值.
【解答】解:∵x+y+z=1,∴z=1﹣(x+y),
∴,
即=10,
设xy=a,x+y=b,则0<a<1,0<b<1,
∴,化简得a=.
∴xyz=xy=a(1﹣b)=(1﹣b) =.
令f(b)=,则f′(b)=,
令f′(b)=0得﹣20b3+47b2﹣36b+9=0,即(4b﹣3)(5b﹣3)(1﹣b)=0,
解得b=或b=或b=1(舍),
∴当0<b<或时,f′(b)>0,
当时,f′(b)<0,
∴f(b)在(0,)上单调递增,在(,)上单调递减,在(,1)上单调递增,
∴当b=时,f(b)取得极大值f()=.
又f(1)=0,
∴f(b)的最大值为.
故答案为.
14.已知函数f(x)=,若函数g(x)=f(x)﹣mx﹣m在(﹣1,1]内有且仅有两个不同的零点,则实数m的取值范围为 (,﹣2]∪(0,] .
【考点】52:函数零点的判定定理.
【分析】由g(x)=f(x)﹣mx﹣m=0,即f(x)=m(x+1),作出两个函数的图象,利用数形结合即可得到结论.
【解答】解:由g(x)=f(x)﹣mx﹣m=0,即f(x)=m(x+1),
分别作出函数f(x)和y=h(x)=m(x+1)的图象如图:
由图象可知f(1)=1,h(x)表示过定点A(﹣1,0)的直线,
当h(x)过(1,1)时,m=,此时两个函数有两个交点,
此时满足条件的m的取值范围是0<m≤,
当h(x)过(0,﹣2)时,h(0)=﹣2,解得m=﹣2,此时两个函数有两个交点,
当h(x)与f(x)相切时,两个函数只有一个交点,此时x﹣3=m(x+1)即m(x+1)2+3(x+1)﹣1=0,
当m=0时,只有1解,当m≠0,由△=9+4m=0得m=﹣,此时直线和f(x)相切,
∴要使函数有两个零点,则﹣<m≤﹣2或0<m≤.
故答案为:(,﹣2]∪(0,].
二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程.
15.已知α∈(,π),且sin+cos=
(1)求sinα的值;
(2)求cos(2α+)的值.
【考点】GI:三角函数的化简求值.
【分析】(1)由sin+cos=两边平方化简整理即可得sinα的值;
(2)由α∈(,π)和sinα的值,即可求出cosα,再由二倍角公式求出sin2α和cos2α,再由两角和的余弦公式计算得答案.
【解答】解:(1)∵sin+cos=,
∴(sin+cos)2=,即.
∴.
∴sinα=;
(2)∵α∈(,π),sinα=,
∴.
∴sin2α=2sinαcosα=,
.
∴cos(2α+)==.
16.已知函数f(x)=loga(x+1)+loga(3﹣x)(a>0且a≠1),且f(1)=2
(1)求a的值及f(x)的定义域;
(2)若不等式f(x)≤c的恒成立,求实数c的取值范围.
【考点】4H:对数的运算性质.
【分析】(1)由f(1)=loga2+loga2=2,解得a=2.可得f(x)=log2(x+1)+log2(3﹣x),由,可得函数f(x)的定义域.
(2)由(1)可知:f(x)=log2(x+1)+log2(3﹣x)=log2(x+1)(3﹣x)=,利用二次函数与对数函数的单调性即可得出.
【解答】解:(1)∵f(1)=loga2+loga2=2,解得a=2.
∴f(x)=log2(x+1)+log2(3﹣x),
由,解得﹣1<x<3,
可得函数f(x)的定义域为:(﹣1,3).
(2)由(1)可知:f(x)=log2(x+1)+log2(3﹣x)=log2(x+1)(3﹣x)==,
可知:当x=1时,函数f(x)取得最大值,f(1)=log24=2.
由不等式f(x)≤c的恒成立,∴c≥2.
∴实数c的取值范围是时,求函数f(x)的值域.
【考点】GL:三角函数中的恒等变换应用.
【分析】(1)利用二倍角和辅助角公式化简为y=Asin(ωx+φ)的形式,再利用周期公式求函数的最小正周期;
(2)根据三角函数的性质即可得f(x)的最大值,以及取得最大值时x取值集合;
(3)当x∈[,]时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的最大值和最小值,即得到f(x)的值域.
【解答】解:函数f(x)=(sinx+cosx)2+2cos2x﹣2
化简可得:f(x)=1+2sinxcosx+1+cos2x﹣2=sin2x+cos2x=sin(2x+)
(1)函数f(x)的最小正周期T=.
(2)令2x+=,k∈Z,
得:x=.
∴当x=时,f(x)取得最大值为.
∴取得最大值时x取值集合为{x|x=,k∈Z}.
(3)当x∈[,]时,
可得:2x+∈[,],
∴﹣1≤sin(2x+)≤
∴≤sin(2x+)≤1.
故得当x∈[,]时,函数f(x)的值域为[,1].
18.如图,在南北方向有一条公路,一半径为100m的圆形广场(圆心为O)与此公路一边所在直线l相切于点A.点P为北半圆弧(弧APB)上的一点,过P作直线l的垂线,垂足为Q.计划在△PAQ内(图中阴影部分)进行绿化.设△PAQ的面积为S(单位:m2).
(1)设∠BOP=α(rad),将S表示为α的函数;
(2)确定点P的位置,使绿化面积最大,并求出最大面积.
【考点】HN:在实际问题中建立三角函数模型;6E:利用导数求闭区间上函数的最值.
【分析】(1)若∠BOP=α,则P点坐标(x,y)中,x=AQ=100sinα,y=PQ=100+100cosα,α∈(0,π),根据三角形面积公式,我们易将S表示为α的函数.
(2)由(1)中结论,我们可利用导数法,判断函数的单调性,进而求出函数的最大值,即最大绿化面积.
【解答】解:(1)AQ=100sinα,PQ=100+100cosα,α∈(0,π),
则△PAQ的面积
=5000(sinα+sinαcosα),(0<α<π).
(2)S/=5000(cosα+cos2α﹣sin2α)
=5000(2cos2α+cosα﹣1)
=5000(2cosα﹣1)(cosα+1),
令,cosα=﹣1(舍去),此时.
当关于α为增函数;
当关于α为减函数.
∴当时,(m2),此时PQ=150m.
答:当点P距公路边界l为150m时,绿化面积最大,
19.已知函数f(x)=ax3+bx2﹣3x(a,b∈R)在点(1,f(1))处的切线方程为y+2=0.
(1)求函数f(x)的解析式;
(2)若对于区间上任意两个自变量的值x1,x2都有|f(x1)﹣f(x2)|≤c,求实数c的最小值;
(3)若过点M(2,m)(m≠2)可作曲线y=f(x)的三条切线,求实数m的取值范围.
【考点】6D:利用导数研究函数的极值;36:函数解析式的求解及常用方法;6H:利用导数研究曲线上某点切线方程.
【分析】(1)由题意,利用导函数的几何含义及切点的实质建立a,b的方程,然后求解即可;
(2)由题意,对于定义域内任意自变量都使得|f(x1)﹣f(x2)|≤c,可以转化为求函数在定义域下的最值即可得解;
(3)由题意,若过点M(2,m)(m≠2)可作曲线y=f(x)的三条切线,等价与函数在切点处导函数值等于切线的斜率这一方程有3解.
【解答】解:(1)f'(x)=3ax2+2bx﹣3.
根据题意,得即解得
所以f(x)=x3﹣3x.
(2)令f'(x)=0,即3x2﹣3=0.得x=±1.
当x∈(﹣∞,﹣1)时,f′(x)>0,函数f(x)在此区间单调递增;
当x∈(﹣1,1)时,f′(x)<0,函数f(x)在此区间单调递减
因为f(﹣1)=2,f(1)=﹣2,
所以当x∈时,f(x)max=2,f(x)min=﹣2.
则对于区间上任意两个自变量的值x1,x2,都有|f(x1)﹣f(x2)|≤|f(x)max﹣f(x)min|=4,所以c≥4.
所以c的最小值为4.
(3)因为点M(2,m)(m≠2)不在曲线y=f(x)上,所以可设切点为(x0,y0).
则y0=x03﹣3x0.
因为f'(x0)=3x02﹣3,所以切线的斜率为3x02﹣3.
则3x02﹣3=,
即2x03﹣6x02+6+m=0.
因为过点M(2,m)(m≠2)可作曲线y=f(x)的三条切线,
所以方程2x03﹣6x02+6+m=0有三个不同的实数解.
所以函数g(x)=2x3﹣6x2+6+m有三个不同的零点.
则g'(x)=6x2﹣12x.令g'(x)=0,则x=0或x=2.
当x∈(﹣∞,0)时,g′(x)>0,函数g(x)在此区间单调递增;当x∈(0,2)时,g′(x)<0,函数g(x)在此区间单调递减;
所以,函数g(x)在x=0处取极大值,在x=2处取极小值,有方程与函数的关系知要满足题意必须满足:
,即,解得﹣6<m<2.
20.已知函数f(x)=xlnx﹣x2﹣x+a,a∈R
(1)当a=0时,求函数f(x)的极值;
(2)若函数f(x)在其定义域内有两个不同的极值点(极值点是指函数取极值时对应的自变量的值),记为x1,x2,且x1<x2.
(ⅰ)求a的取值范围;
(ⅱ)若不等式e1+λ<x1 x恒成立,求正实数λ的取值范围.
【考点】6D:利用导数研究函数的极值;6B:利用导数研究函数的单调性.
【分析】(1)求出f(x)的解析式,求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极小值即可;
(2)(i)由导数与极值的关系知可转化为方程f′(x)=lnx﹣ax=0在(0,+∞)有两个不同根;再转化为函数y=lnx与函数y=ax的图象在(0,+∞)上有两个不同交点,或转化为函数g(x)=与函数y=a的图象在(0,+∞)上有两个不同交点;或转化为g(x)=lnx﹣ax有两个不同零点,从而讨论求解;
(ii)e1+λ<x1 x2λ可化为1+λ<lnx1+λlnx2,结合方程的根知1+λ<ax1+λax2=a(x1+λx2),从而可得a>;而a=,从而可得ln
<恒成立;再令t=,t∈(0,1),从而可得不等式lnt<在t∈(0,1)上恒成立,再令h(t)=lnt﹣,从而利用导数化恒成立问题为最值问题即可.
【解答】解:(1)a=0时,f(x)=xlnx﹣x,函数的定义域是(0,+∞),
f(x)=lnx,令f′(x)>0,解得:x>1,令f′(x)<0,解得:0<x<1,
故函数在(0,1)递减,在(1,+∞)递增,
故函数的极小值是f(1)=﹣1;
(2)(i)由题意知,函数f(x)的定义域为(0,+∞),
方程f′(x)=0在(0,+∞)有两个不同根;
即方程lnx﹣ax=0在(0,+∞)有两个不同根;
(解法一)转化为函数y=lnx与函数y=ax的图象在(0,+∞)上有两个不同交点,
如右图.
可见,若令过原点且切于函数y=lnx图象的直线斜率为k,只须0<a<k.
令切点A(x0,lnx0),
故k=y′|x=x0=,又k=,
故=,解得,x0=e,
故k=,故0<a<.
(解法二)转化为函数g(x)=与函数y=a的图象在(0,+∞)上有两个不同交点
又g′(x)=,
即0<x<e时,g′(x)>0,x>e时,g′(x)<0,
故g(x)在(0,e)上单调增,在(e,+∞)上单调减.
故g(x)极大=g(e)=;
又g(x)有且只有一个零点是1,且在x→0时,g(x)→﹣∞,在在x→+∞时,g(x)→0,
故g(x)的草图如右图,
可见,要想函数g(x)=与函数y=a的图象在(0,+∞)上有两个不同交点,
只须0<a<.
(解法三)令g(x)=lnx﹣ax,从而转化为函数g(x)有两个不同零点,
而g′(x)=﹣ax=(x>0),
若a≤0,可见g′(x)>0在(0,+∞)上恒成立,所以g(x)在(0,+∞)单调增,
此时g(x)不可能有两个不同零点.
若a>0,在0<x<时,g′(x)>0,在x>时,g′(x)<0,
所以g(x)在(0,)上单调增,在(,+∞)上单调减,从而g(x)极大值=g()=ln﹣1,
又因为在x→0时,g(x)→﹣∞,在在x→+∞时,g(x)→﹣∞,
于是只须:g(x)极大>0,即ln﹣1>0,所以0<a<.
综上所述,0<a<.
(ii)因为e1+λ<x1 x2λ等价于1+λ<lnx1+λlnx2.
由(i)可知x1,x2分别是方程lnx﹣ax=0的两个根,
即lnx1=ax1,lnx2=ax2
所以原式等价于1+λ<ax1+λax2=a(x1+λx2),因为λ>0,0<x1<x2,
所以原式等价于a>,
又由lnx1=ax1,lnx2=ax2作差得,ln
=a(x1﹣x2),
即a=,所以原式等价于>,
因为0<x1<x2,原式恒成立,即ln<恒成立,
令t=,t∈(0,1),
则不等式lnt<在t∈(0,1)上恒成立.
令h(t)=lnt﹣,
又h′(t)=,
当λ2≥1时,可见t∈(0,1)时,h′(t)>0,
所以h(t)在t∈(0,1)上单调增,又h(1)=0,h(t)<0在t∈(0,1)恒成立,符合题意.
当λ2<1时,可见t∈(0,λ2)时,h′(t)>0,t∈(λ2,1)时h′(t)<0,
所以h(t)在t∈(0,λ2)时单调增,在t∈(λ2,1)时单调减,又h(1)=0,
所以h(t)在t∈(0,1)上不能恒小于0,不符合题意,舍去.
综上所述,若不等式e1+λ<x1 x2λ恒成立,只须λ2≥1,又λ>0,所以λ≥1.
同课章节目录
