九年级数学下册 3.1圆 教案 新版北师大版
文档属性
| 名称 | 九年级数学下册 3.1圆 教案 新版北师大版 |  | |
| 格式 | zip | ||
| 文件大小 | 637.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-18 10:37:30 | ||
图片预览


文档简介
3.1圆
一、教学目标
1.知道圆的有关定义及表示方法.
2.掌握点和圆的位置关系.
3.会根据要求画出图形.
二、课时安排
1课时
三、教学重点
点和圆的位置关系.
四、教学难点
点和圆的位置关系.
五、教学过程
(一)导入新课
生活中关于圆的图形展示,引导学生认识圆并谈谈对圆的理解:
(二)讲授新课
活动1:小组合作
观察车轮,你发现了什么?
车轮为什么做成圆形
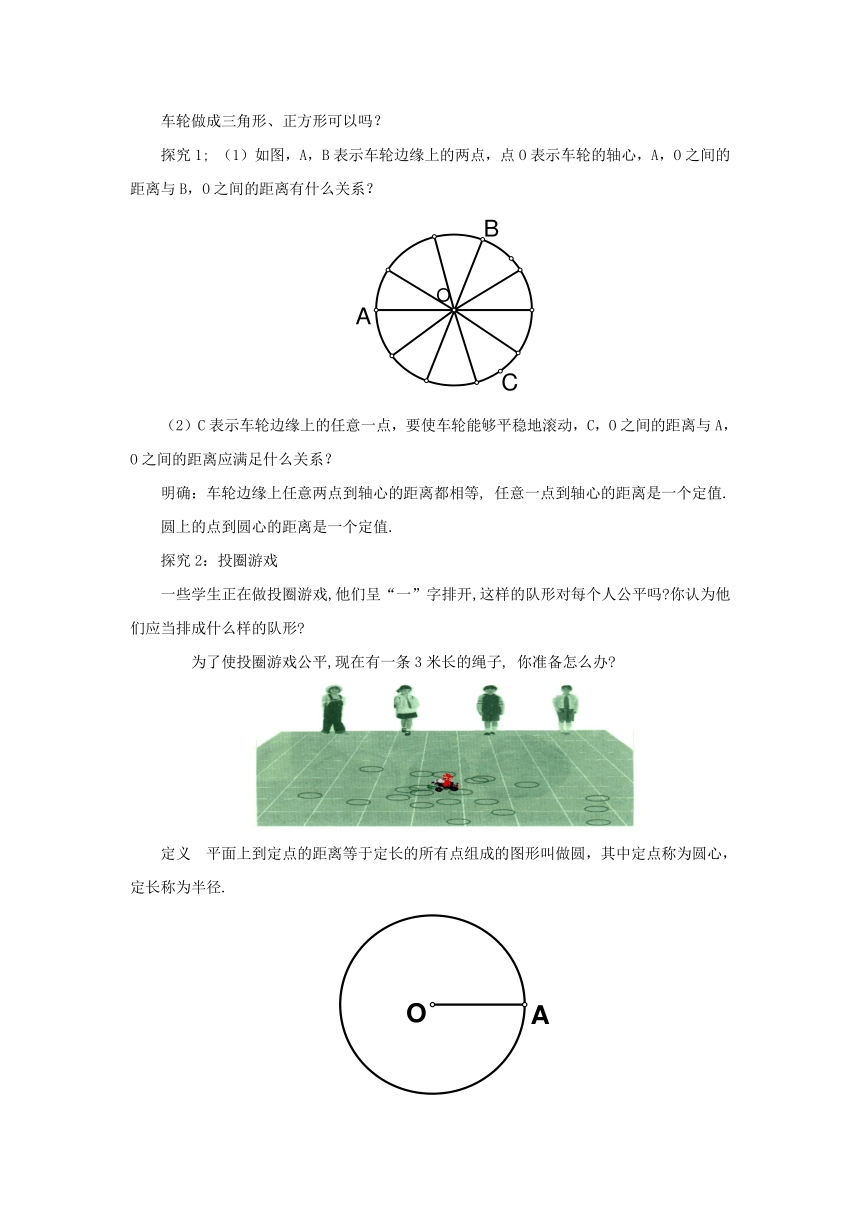
车轮做成三角形、正方形可以吗?
探究1;
(1)如图,A,B表示车轮边缘上的两点,点O表示车轮的轴心,A,O之间的距离与B,O之间的距离有什么关系?
(2)C表示车轮边缘上的任意一点,要使车轮能够平稳地滚动,C,O之间的距离与A,O之间的距离应满足什么关系?
明确:车轮边缘上任意两点到轴心的距离都相等,
任意一点到轴心的距离是一个定值.
圆上的点到圆心的距离是一个定值.
探究2:投圈游戏
一些学生正在做投圈游戏,他们呈“一”字排开,这样的队形对每个人公平吗 你认为他们应当排成什么样的队形
为了使投圈游戏公平,现在有一条3米长的绳子,
你准备怎么办
定义
平面上到定点的距离等于定长的所有点组成的图形叫做圆,其中定点称为圆心,定长称为半径.
注意:1.从圆的定义可知:圆是指圆周而不是圆面.
2.确定圆的要素是:圆心、半径.
圆心确定圆的位置,半径确定圆的大小,确定一个圆,两者缺一不可.
以点O为圆心的圆记作:⊙O,读作:“圆O”.
探究3:圆的有关性质
战国时期的《墨经》一书中记载:“圜,一中同长也
”.古代的圜(huán)即圆,这句话是圆的定义,它的意思是:
圆是从中心到周界各点有相同长度的图形.
提问:
如果一个点到圆心距离小于半径,
那么这个点在哪里呢 大于圆的半径呢 反过来呢
试根据圆的定义填空:
1.圆上各点到________________的距离都等于______
_____________.
2.到定点的距离等于定长的点都在_________.
探究4:点与圆的位置关系
如图,设⊙O的半径为r,A点在圆内,B点在圆上,C点在圆外,那么OA<r,
OB=r,
OC>r.
结论:点的位置可以确定该点到圆心的距离与半径的关系,反过来,已知点到圆心的距离与半径的关系也可以确定该点与圆的位置关系.
画图:已知Rt△ABC,AB2.根据图形回答下列问题:
(1)看图想一想,Rt△ABC的各个顶点与⊙B在位置上有什么关系?
答:点A在圆上.点B在圆内.点C在圆外
(2)在以上三种关系中,点到圆心的距离与圆的半径在数量上有什么关系?
活动2:探究归纳
点在圆外,这个点到圆心的距离大于半径.
点在圆上,这个点到圆心的距离等于半径.
点在圆内,这个点到圆心的距离小于半径.
(三)重难点精讲
例1.已知⊙O的半径r=2cm,
当OP
时,点P在⊙O上;
当OA=1cm时,点A在
;
当OB=4cm时,点B在
.
答案:=2cm;
⊙O内;
⊙O外
例2.已知:如图,矩形ABCD的对角线相交于点O,试猜想:矩形的四个顶点能在同一个圆上吗?
答:在矩形ABCD中,有OA=OB=OC=OD,四个顶点在同一个圆上,故矩形四个顶点能在同一个圆上.
(四)归纳小结
通过本课时的学习,需要我们掌握:
1.从运动和集合的观点理解圆的定义.
2.点与圆的位置关系.
3.证明几个点在同一个圆上的方法.
(五)随堂检测
1.(上海·中考)矩形ABCD中,AB=8,,点P在边AB上,且BP=3AP,如果圆P是以点P为圆心,PD为半径的圆,那么下列判断正确的是(
)
A.点B,C均在圆P外
B.点B在圆P外、点C在圆P内
C.点B在圆P内、点C在圆P外
D.点B,C均在圆P内
2.(新疆建设兵团·中考)如图,王大爷家屋后有一块长12m,宽8m的矩形空地,他在以BC为直径的半圆内种菜,他家养的一只羊平时拴在A处,为了不让羊吃到菜,拴羊的绳子可以选用(
)
A.3m
B.5m
C.7m
D.9m
3.(泉州·中考)
已知三角形的三边长分别为3,4,5,则它的边与半径为1的圆的公共点个数所有可能的情况是________.(写出符合的一种情况即可)
【答案】
1.
【解析】选C.由题意知,PB=6,PA=2,PD=7,
PC=9,所以点B在圆P内、点C在圆P外.
2.
答案:A
3.
【解析】∵圆心的位置不确定,∴交点个数共有5种情况即0、1、2、3、4.故答案为0或1或2或3、4.
答案:2(符合答案即可)
六.板书设计
3.1圆
1.判断点与圆的位置关系的方法:
设⊙O的半径为r,则点P与⊙O的位置关系有
(1)点P在⊙O上
OP=r
(2)点P在⊙O内
OP<r
(3)点P在⊙O外
OP>r
2.要证明几个点在同一个圆上,只要证明这几个点到同一个定点的距离相等.
七、作业布置
课本P66练习
练习册相关练习
八、教学反思
一、教学目标
1.知道圆的有关定义及表示方法.
2.掌握点和圆的位置关系.
3.会根据要求画出图形.
二、课时安排
1课时
三、教学重点
点和圆的位置关系.
四、教学难点
点和圆的位置关系.
五、教学过程
(一)导入新课
生活中关于圆的图形展示,引导学生认识圆并谈谈对圆的理解:
(二)讲授新课
活动1:小组合作
观察车轮,你发现了什么?
车轮为什么做成圆形
车轮做成三角形、正方形可以吗?
探究1;
(1)如图,A,B表示车轮边缘上的两点,点O表示车轮的轴心,A,O之间的距离与B,O之间的距离有什么关系?
(2)C表示车轮边缘上的任意一点,要使车轮能够平稳地滚动,C,O之间的距离与A,O之间的距离应满足什么关系?
明确:车轮边缘上任意两点到轴心的距离都相等,
任意一点到轴心的距离是一个定值.
圆上的点到圆心的距离是一个定值.
探究2:投圈游戏
一些学生正在做投圈游戏,他们呈“一”字排开,这样的队形对每个人公平吗 你认为他们应当排成什么样的队形
为了使投圈游戏公平,现在有一条3米长的绳子,
你准备怎么办
定义
平面上到定点的距离等于定长的所有点组成的图形叫做圆,其中定点称为圆心,定长称为半径.
注意:1.从圆的定义可知:圆是指圆周而不是圆面.
2.确定圆的要素是:圆心、半径.
圆心确定圆的位置,半径确定圆的大小,确定一个圆,两者缺一不可.
以点O为圆心的圆记作:⊙O,读作:“圆O”.
探究3:圆的有关性质
战国时期的《墨经》一书中记载:“圜,一中同长也
”.古代的圜(huán)即圆,这句话是圆的定义,它的意思是:
圆是从中心到周界各点有相同长度的图形.
提问:
如果一个点到圆心距离小于半径,
那么这个点在哪里呢 大于圆的半径呢 反过来呢
试根据圆的定义填空:
1.圆上各点到________________的距离都等于______
_____________.
2.到定点的距离等于定长的点都在_________.
探究4:点与圆的位置关系
如图,设⊙O的半径为r,A点在圆内,B点在圆上,C点在圆外,那么OA<r,
OB=r,
OC>r.
结论:点的位置可以确定该点到圆心的距离与半径的关系,反过来,已知点到圆心的距离与半径的关系也可以确定该点与圆的位置关系.
画图:已知Rt△ABC,AB
(1)看图想一想,Rt△ABC的各个顶点与⊙B在位置上有什么关系?
答:点A在圆上.点B在圆内.点C在圆外
(2)在以上三种关系中,点到圆心的距离与圆的半径在数量上有什么关系?
活动2:探究归纳
点在圆外,这个点到圆心的距离大于半径.
点在圆上,这个点到圆心的距离等于半径.
点在圆内,这个点到圆心的距离小于半径.
(三)重难点精讲
例1.已知⊙O的半径r=2cm,
当OP
时,点P在⊙O上;
当OA=1cm时,点A在
;
当OB=4cm时,点B在
.
答案:=2cm;
⊙O内;
⊙O外
例2.已知:如图,矩形ABCD的对角线相交于点O,试猜想:矩形的四个顶点能在同一个圆上吗?
答:在矩形ABCD中,有OA=OB=OC=OD,四个顶点在同一个圆上,故矩形四个顶点能在同一个圆上.
(四)归纳小结
通过本课时的学习,需要我们掌握:
1.从运动和集合的观点理解圆的定义.
2.点与圆的位置关系.
3.证明几个点在同一个圆上的方法.
(五)随堂检测
1.(上海·中考)矩形ABCD中,AB=8,,点P在边AB上,且BP=3AP,如果圆P是以点P为圆心,PD为半径的圆,那么下列判断正确的是(
)
A.点B,C均在圆P外
B.点B在圆P外、点C在圆P内
C.点B在圆P内、点C在圆P外
D.点B,C均在圆P内
2.(新疆建设兵团·中考)如图,王大爷家屋后有一块长12m,宽8m的矩形空地,他在以BC为直径的半圆内种菜,他家养的一只羊平时拴在A处,为了不让羊吃到菜,拴羊的绳子可以选用(
)
A.3m
B.5m
C.7m
D.9m
3.(泉州·中考)
已知三角形的三边长分别为3,4,5,则它的边与半径为1的圆的公共点个数所有可能的情况是________.(写出符合的一种情况即可)
【答案】
1.
【解析】选C.由题意知,PB=6,PA=2,PD=7,
PC=9,所以点B在圆P内、点C在圆P外.
2.
答案:A
3.
【解析】∵圆心的位置不确定,∴交点个数共有5种情况即0、1、2、3、4.故答案为0或1或2或3、4.
答案:2(符合答案即可)
六.板书设计
3.1圆
1.判断点与圆的位置关系的方法:
设⊙O的半径为r,则点P与⊙O的位置关系有
(1)点P在⊙O上
OP=r
(2)点P在⊙O内
OP<r
(3)点P在⊙O外
OP>r
2.要证明几个点在同一个圆上,只要证明这几个点到同一个定点的距离相等.
七、作业布置
课本P66练习
练习册相关练习
八、教学反思
