湖南省张家界市2016-2017学年高一数学下学期期末试卷(b卷)(含解析)
文档属性
| 名称 | 湖南省张家界市2016-2017学年高一数学下学期期末试卷(b卷)(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 259.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-19 22:19:25 | ||
图片预览




文档简介
2016-2017学年湖南省张家界市高一(下)期末数学试卷(B卷)
一、选择题:本大题共12小题,每小题5分,满分60分.
1.1和5的等差中项是( )
A.
B.
C.3
D.±3
2.设a>b,则下列不等式中正确的是( )
A.
B.a+c>b+c
C.ac2>bc2
D.a2>b2
3.直线l经过原点O和点P(1,1),则其斜率为( )
A.1
B.﹣1
C.﹣2
D.2
4.下列结论中正确的是( )
A.经过三点确定一个平面
B.平行于同一平面的两条直线平行
C.垂直于同一直线的两条直线平行
D.垂直于同一平面的两条直线平行
5.空间两点A(1,2,﹣2),B(﹣1,0,﹣1)之间的距离为( )
A.5
B.3
C.2
D.1
6.如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是( )
A.6
B.3
C.12
D.6
7.在△ABC中,面积,c=2,B=60°,则a=( )
A.2
B.
C.
D.1
8.圆x2+y2=4与圆(x﹣3)2+y2=1的位置关系为( )
A.内切
B.相交
C.外切
D.相离
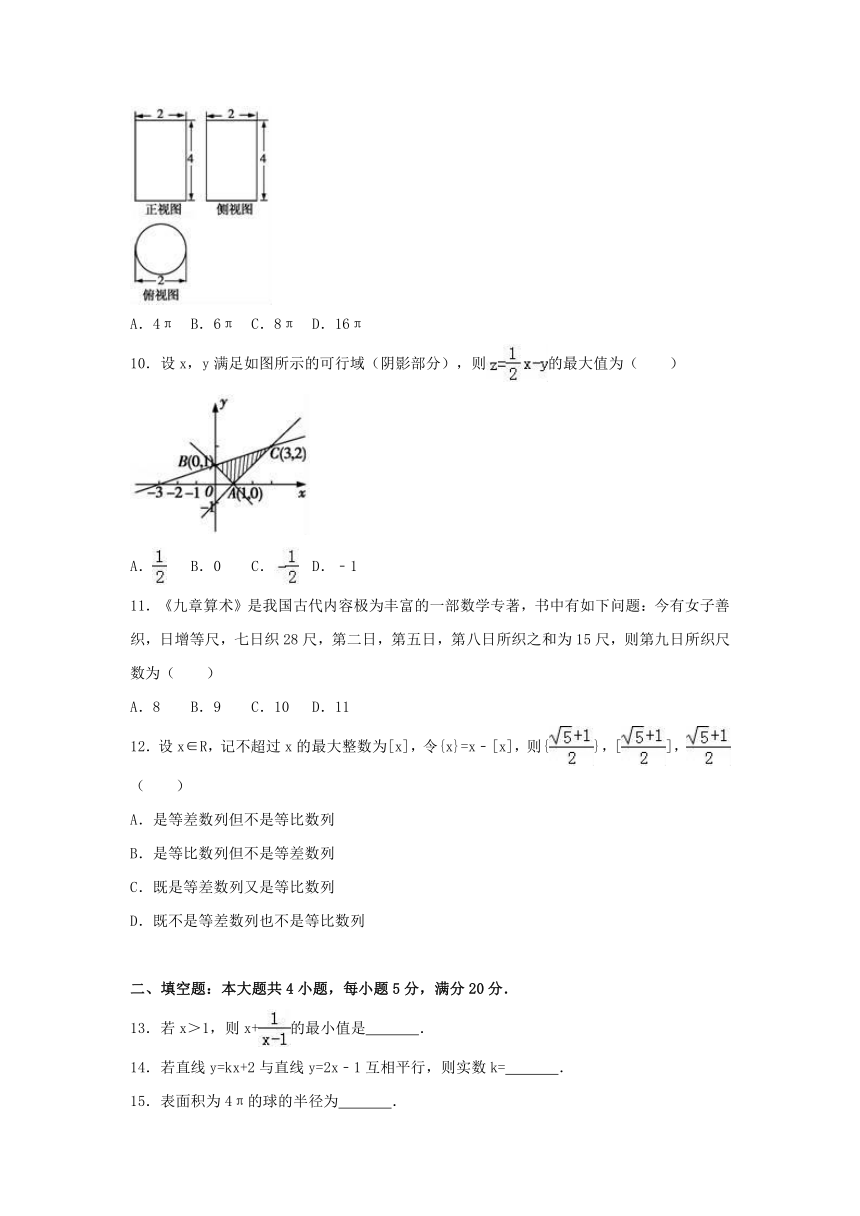
9.已知一个几何体的三视图如图所示,则该几何体的体积为( )
A.4π
B.6π
C.8π
D.16π
10.设x,y满足如图所示的可行域(阴影部分),则的最大值为( )
A.
B.0
C.
D.﹣1
11.《九章算术》是我国古代内容极为丰富的一部数学专著,书中有如下问题:今有女子善织,日增等尺,七日织28尺,第二日,第五日,第八日所织之和为15尺,则第九日所织尺数为( )
A.8
B.9
C.10
D.11
12.设x∈R,记不超过x的最大整数为[x],令{x}=x﹣[x],则{},[],( )
A.是等差数列但不是等比数列
B.是等比数列但不是等差数列
C.既是等差数列又是等比数列
D.既不是等差数列也不是等比数列
二、填空题:本大题共4小题,每小题5分,满分20分.
13.若x>1,则x+的最小值是
.
14.若直线y=kx+2与直线y=2x﹣1互相平行,则实数k=
.
15.表面积为4π的球的半径为
.
16.△ABC的三边a,b,c成等比数列,则角B的范围是
.
三、解答题:本大题共6小题,满分70分.解答应写出文字说明、证明过程或演算步骤.
17.已知直线l1:3x+4y﹣2=0,l2:2x+y+2=0相交于点P.
(1)求点P的坐标;
(2)求过点P且与直线x﹣2y﹣1=0垂直的直线l的方程.
18.已知不等式(1﹣a)x2﹣4x+6>0的解集为{x|﹣3<x<1}.
(1)求a的值;
(2)若不等式ax2+mx+3≥0的解集为R,求实数m的取值范围.
19.已知数列{an}是等差数列,其前n项和为Sn,且a3=6,S3=12,设.
(1)求an;
(2)求数列{bn}的前n项和Tn.
20.如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,PA=AB=BC=2,AD=4.
(1)求四棱锥P﹣ABCD的体积;
(2)求证:CD⊥平面PAC.
21.△ABC中,角A,B,C的对边分别为a,b,c,已知.
(Ⅰ)求角B的大小;
(Ⅱ)点D为边AB上的一点,记∠BDC=θ,若<θ<π,CD=2,,a=,求sinθ与b的值.
22.已知圆C:(x﹣3)2+(y﹣4)2=4,直线l1过定点A
(1,0).
(Ⅰ)若l1与圆C相切,求l1的方程;
(Ⅱ)若l1与圆C相交于P,Q两点,求三角形CPQ的面积的最大值,并求此时直线l1的方程.
2016-2017学年湖南省张家界市高一(下)期末数学试卷(B卷)
参考答案与试题解析
一、选择题:本大题共12小题,每小题5分,满分60分.
1.1和5的等差中项是( )
A.
B.
C.3
D.±3
【考点】84:等差数列的通项公式.
【分析】由a,b,c成等差数列,可得2b=a+c,计算即可得到所求值.
【解答】解:1和5的等差中项为=3,
故选:C.
2.设a>b,则下列不等式中正确的是( )
A.
B.a+c>b+c
C.ac2>bc2
D.a2>b2
【考点】R3:不等式的基本性质.
【分析】根据题意,依次分析四个选项中的不等式,综合即可得答案.
【解答】解:根据题意,依次分析选项:
对于A,当a=2,b=1时,有<,故A错误;
对于B、不等式两边加(或减)同一个数(或式子),不等号的方向不变,故B正确;
对于C、当c=0时,ac2=bc2,故C错误;
对于D、当a=1,b=﹣2时,a2=1,b2=4,此时a2<b2,故D错误;
故选:B.
3.直线l经过原点O和点P(1,1),则其斜率为( )
A.1
B.﹣1
C.﹣2
D.2
【考点】I3:直线的斜率.
【分析】根据题意,由直线斜率的计算公式直接计算即可得答案.
【解答】解:根据题意,直线l经过原点O和点P(1,1),
则其斜率k==1;
故选:A.
4.下列结论中正确的是( )
A.经过三点确定一个平面
B.平行于同一平面的两条直线平行
C.垂直于同一直线的两条直线平行
D.垂直于同一平面的两条直线平行
【考点】LP:空间中直线与平面之间的位置关系.
【分析】A,经过不共线的三点才可以确定一个平面,
B,平行于同一平面的两条直线可能平行、相交、异面;
C,垂直于同一直线的两条直线可能平行、相交、异面;
D,根据直线与平面垂直的性质定理直接可得答案,
【解答】解:对于A,经过不共线的三点才可以确定一个平面,故错,
对于B,平行于同一平面的两条直线可能平行、相交、异面,故错;
对于C,垂直于同一直线的两条直线可能平行、相交、异面,故错;
对于D,根据直线与平面垂直的性质定理,可得垂直于同一平面的两条直线平行,故正确.
故选:D
5.空间两点A(1,2,﹣2),B(﹣1,0,﹣1)之间的距离为( )
A.5
B.3
C.2
D.1
【考点】JI:空间两点间的距离公式.
【分析】根据空间中两点间的距离公式计算即可.
【解答】解:空间两点A(1,2,﹣2),B(﹣1,0,﹣1)之间的距离为
|AB|==3.
故选:B.
6.如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是( )
A.6
B.3
C.12
D.6
【考点】LD:斜二测法画直观图.
【分析】画出△OAB的直观图,根据数据求出直观图的面积.
【解答】解:△O′A′B′是水平放置的△OAB的直观图,
所以:S△OAB==12
故选C.
7.在△ABC中,面积,c=2,B=60°,则a=( )
A.2
B.
C.
D.1
【考点】HT:三角形中的几何计算.
【分析】利用,能求出a.
【解答】解:在△ABC中,
∵面积,c=2,B=60°,
∴,即,
解得a=1.
故选:D.
8.圆x2+y2=4与圆(x﹣3)2+y2=1的位置关系为( )
A.内切
B.相交
C.外切
D.相离
【考点】JA:圆与圆的位置关系及其判定.
【分析】根据题意,由两圆的标准方程分析可得两圆的圆心与半径,分析计算两圆的圆心距与半径和之间的关系,即可得答案.
【解答】解:根据题意,设圆x2+y2=4的圆心为M,半径为r1,则M(0,0),r1=2,
圆(x﹣3)2+y2=1的圆心为N,半径为r2,N(3,0),r2=1,
则有|MN|=r1+r2=3,
则两圆外切;
故选:C.
9.已知一个几何体的三视图如图所示,则该几何体的体积为( )
A.4π
B.6π
C.8π
D.16π
【考点】L!:由三视图求面积、体积.
【分析】由三视图还原原几何体,可知原几何体是底面半径为1,高为4的圆柱,再由圆柱体积公式得答案.
【解答】解:由三视图还原原几何体如图:
该几何体是底面半径为1,高为4的圆柱,
则其体积为π×12×4=4π.
故选:A.
10.设x,y满足如图所示的可行域(阴影部分),则的最大值为( )
A.
B.0
C.
D.﹣1
【考点】7C:简单线性规划.
【分析】把目标函数化为y=x﹣z,平移直线y=x﹣z找出最优解,求出目标函数的最大值.
【解答】解:x,y满足如图所示的可行域(阴影部分),
则目标函数可化为y=x﹣z,
平移直线y=x﹣z,
当直线y=x﹣z过点A(1,0)时,
z取得最大值为zmax=×1﹣0=.
故选:A.
11.《九章算术》是我国古代内容极为丰富的一部数学专著,书中有如下问题:今有女子善织,日增等尺,七日织28尺,第二日,第五日,第八日所织之和为15尺,则第九日所织尺数为( )
A.8
B.9
C.10
D.11
【考点】84:等差数列的通项公式.
【分析】由题意可知,每日所织数量构成等差数列,再由已知求得a5,a4的值,进一步求得公差,代入等差数列的通项公式求得第九日所织尺数.
【解答】解:由题意可知,每日所织数量构成等差数列,且a2+a5+a8=15,S7=28,
设公差为d,由a2+a5+a8=15,得3a5=15,∴a5=5,
由S7=28,得7a4=28,∴a4=4,则d=a5﹣a4=1,
∴a9=a5+4d=5+4×1=9.
故选:B.
12.设x∈R,记不超过x的最大整数为[x],令{x}=x﹣[x],则{},[],( )
A.是等差数列但不是等比数列
B.是等比数列但不是等差数列
C.既是等差数列又是等比数列
D.既不是等差数列也不是等比数列
【考点】8C:等差关系的确定;8D:等比关系的确定.
【分析】可分别求得,.则等比数列性质易得三者构成等比数列.
【解答】解:根据题意可得,.
∵×=12,
+≠2
∴{},[],为等比数列,不是等差数列
故选B.
二、填空题:本大题共4小题,每小题5分,满分20分.
13.若x>1,则x+的最小值是 3 .
【考点】7F:基本不等式.
【分析】x+=x﹣1++1,利用基本不等式可求函数的最值.
【解答】解:∵x>1,
∴x+=x﹣1++1+1=3,
当且仅当x﹣1=即x=2时取等号,
∴x=2时x+取得最小值3,
故答案为:3.
14.若直线y=kx+2与直线y=2x﹣1互相平行,则实数k= 2 .
【考点】II:直线的一般式方程与直线的平行关系.
【分析】利用直线平行的性质直接求解.
【解答】解:∵直线y=kx+2与直线y=2x﹣1互相平行,
∴实数k=2.
故答案为:2.
15.表面积为4π的球的半径为 1 .
【考点】LG:球的体积和表面积.
【分析】由球的表面积公式S=4πR2,直接计算.
【解答】解:设球的半径为R,由球的表面积公式S=4πR2=4π,解得R=1.
故答案为:1
16.△ABC的三边a,b,c成等比数列,则角B的范围是 0<B≤ .
【考点】8B:数列的应用.
【分析】根据题中已知条件求出a,b,c之间的关系,然后利用余弦定理便可求出cosB的值,即可求出角B的范围.
【解答】解:由题意知:a,b,c成等比数列,
∴b2=ac,
又∵a,b,c是三角形的三边,不妨设a≤b≤c,
由余弦定理得
故有,
故答案为.
三、解答题:本大题共6小题,满分70分.解答应写出文字说明、证明过程或演算步骤.
17.已知直线l1:3x+4y﹣2=0,l2:2x+y+2=0相交于点P.
(1)求点P的坐标;
(2)求过点P且与直线x﹣2y﹣1=0垂直的直线l的方程.
【考点】IK:待定系数法求直线方程;IM:两条直线的交点坐标.
【分析】(1)把两条直线的方程联立方程组,求得该方程组的解,即可求得交点P的坐标.
(2)利用两条直线垂直的性质求得直线l的斜率,再用点斜式求出直线l的方程.
【解答】(1)由,求得,∴两条直线的交点坐标为
P(﹣2,2).
(2)直线x﹣2y﹣1=0的斜率为,故要求的直线l的斜率为﹣2,故要求的直线的方程为y﹣2=﹣2(x+2),
即直线l的方程为2x+y+2=0.
18.已知不等式(1﹣a)x2﹣4x+6>0的解集为{x|﹣3<x<1}.
(1)求a的值;
(2)若不等式ax2+mx+3≥0的解集为R,求实数m的取值范围.
【考点】74:一元二次不等式的解法.
【分析】(1)一元二次不等式与对应方程的关系,旅游根与系数的关系求出a的值;
(2)根据一元二次不等式解集为R,利用判别式△≤0,求出m的取值范围.
【解答】解:(1)不等式(1﹣a)x2﹣4x+6>0的解集为{x|﹣3<x<1},
∴1﹣a<0,且方程(1﹣a)x2﹣4x+6=0的两根为﹣3,1;
由根与系数的关系知,
解得a=3;…
(2)不等式3x2+mx+3≥0的解集为R,
则△=m2﹣4×3×3≤0,
解得﹣6≤m≤6,
∴实数m的取值范围为(﹣6,6).…
19.已知数列{an}是等差数列,其前n项和为Sn,且a3=6,S3=12,设.
(1)求an;
(2)求数列{bn}的前n项和Tn.
【考点】8E:数列的求和;8H:数列递推式.
【分析】(1)设数列{an}是公差为d的等差数列,运用等差数列的通项公式和求和公式,解方程可得首项和公差,即可得到所求通项;
(2)求出=4n,运用等比数列的求和公式,化简计算即可得到所求和.
【解答】解:(1)设数列{an}是公差为d的等差数列,
;
(2),
可得Tn=b1+b2+b3+…+bn=4+42+43+…+4n
=.
20.如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,PA=AB=BC=2,AD=4.
(1)求四棱锥P﹣ABCD的体积;
(2)求证:CD⊥平面PAC.
【考点】LF:棱柱、棱锥、棱台的体积;LW:直线与平面垂直的判定.
【分析】(1)由四边形ABCD是直角梯形,PA⊥底面ABCD,能求出四棱锥P﹣ABCD的体积.
(2)由PA⊥底面ABCD,得PA⊥CD,由勾股定理得AC⊥CD,由此能证明CD⊥平面PAC.
【解答】解:(1)由已知,四边形ABCD是直角梯形,
∴,
∵PA⊥底面ABCD,
∴四棱锥P﹣ABCD的体积.…
证明:(2)由PA⊥底面ABCD,CD 底面ABCD,则PA⊥CD,
在三角形ABC中,,
又,∴AC2+CD2=AD2,即AC⊥CD,…
又∵PA,AC 平面PAC,PA∩AC=A,
∴CD⊥平面PAC.…
21.△ABC中,角A,B,C的对边分别为a,b,c,已知.
(Ⅰ)求角B的大小;
(Ⅱ)点D为边AB上的一点,记∠BDC=θ,若<θ<π,CD=2,,a=,求sinθ与b的值.
【考点】HR:余弦定理;HP:正弦定理.
【分析】(Ⅰ)由正弦定理,同角三角函数基本关系式化简已知等式可得tanB=,结合范围0<B<π,可求B的值.
(Ⅱ)在△BCD中,由正弦定理可得=,解得sinθ=,结合θ为钝角,利用诱导公式可求cos∠ADC的值,在△ADC中,由余弦定理,可得b的值.
【解答】(本题满分为12分)
解:(Ⅰ)∵,∴可得:,
∵sinC>0,∴
=tanB=,
∵0<B<π,
∴B=…4分
(Ⅱ)在△BCD中,∵
=,
∴=,∴sinθ=,…8分
∵θ为钝角,
∴∠ADC为锐角,
∴cos∠ADC=cos(π﹣θ)==,
∴在△ADC中,由余弦定理,可得:
b===…12分
22.已知圆C:(x﹣3)2+(y﹣4)2=4,直线l1过定点A
(1,0).
(Ⅰ)若l1与圆C相切,求l1的方程;
(Ⅱ)若l1与圆C相交于P,Q两点,求三角形CPQ的面积的最大值,并求此时直线l1的方程.
【考点】J7:圆的切线方程;IT:点到直线的距离公式.
【分析】(Ⅰ)通过直线l1的斜率存在与不存在两种情况,利用直线的方程与圆C相切,圆心到直线的距离等于半径,即可求l1的方程;
(Ⅱ)设直线方程为kx﹣y﹣k=0,求出圆心到直线的距离,弦长,得到三角形CPQ的面积的表达式,利用二次函数求出面积的最大值时的距离,然后求出直线的斜率,即可得到l1的直线方程.
【解答】解:(Ⅰ)
①若直线l1的斜率不存在,则直线l1:x=1,符合题意.
②若直线l1斜率存在,设直线l1的方程为y=k(x﹣1),即kx﹣y﹣k=0.
由题意知,圆心(3,4)到已知直线l1的距离等于半径2,
即:,解之得.
所求直线l1的方程是x=1或3x﹣4y﹣3=0.
(Ⅱ)直线与圆相交,斜率必定存在,且不为0,设直线方程为kx﹣y﹣k=0,
则圆心到直l1的距离d=
又∵三角形CPQ面积S=×2=d=
∴当d=时,S取得最大值2.
∴d==,k=1或k=7.
∴直线方程为y=x﹣1,或y=7x﹣7.
一、选择题:本大题共12小题,每小题5分,满分60分.
1.1和5的等差中项是( )
A.
B.
C.3
D.±3
2.设a>b,则下列不等式中正确的是( )
A.
B.a+c>b+c
C.ac2>bc2
D.a2>b2
3.直线l经过原点O和点P(1,1),则其斜率为( )
A.1
B.﹣1
C.﹣2
D.2
4.下列结论中正确的是( )
A.经过三点确定一个平面
B.平行于同一平面的两条直线平行
C.垂直于同一直线的两条直线平行
D.垂直于同一平面的两条直线平行
5.空间两点A(1,2,﹣2),B(﹣1,0,﹣1)之间的距离为( )
A.5
B.3
C.2
D.1
6.如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是( )
A.6
B.3
C.12
D.6
7.在△ABC中,面积,c=2,B=60°,则a=( )
A.2
B.
C.
D.1
8.圆x2+y2=4与圆(x﹣3)2+y2=1的位置关系为( )
A.内切
B.相交
C.外切
D.相离
9.已知一个几何体的三视图如图所示,则该几何体的体积为( )
A.4π
B.6π
C.8π
D.16π
10.设x,y满足如图所示的可行域(阴影部分),则的最大值为( )
A.
B.0
C.
D.﹣1
11.《九章算术》是我国古代内容极为丰富的一部数学专著,书中有如下问题:今有女子善织,日增等尺,七日织28尺,第二日,第五日,第八日所织之和为15尺,则第九日所织尺数为( )
A.8
B.9
C.10
D.11
12.设x∈R,记不超过x的最大整数为[x],令{x}=x﹣[x],则{},[],( )
A.是等差数列但不是等比数列
B.是等比数列但不是等差数列
C.既是等差数列又是等比数列
D.既不是等差数列也不是等比数列
二、填空题:本大题共4小题,每小题5分,满分20分.
13.若x>1,则x+的最小值是
.
14.若直线y=kx+2与直线y=2x﹣1互相平行,则实数k=
.
15.表面积为4π的球的半径为
.
16.△ABC的三边a,b,c成等比数列,则角B的范围是
.
三、解答题:本大题共6小题,满分70分.解答应写出文字说明、证明过程或演算步骤.
17.已知直线l1:3x+4y﹣2=0,l2:2x+y+2=0相交于点P.
(1)求点P的坐标;
(2)求过点P且与直线x﹣2y﹣1=0垂直的直线l的方程.
18.已知不等式(1﹣a)x2﹣4x+6>0的解集为{x|﹣3<x<1}.
(1)求a的值;
(2)若不等式ax2+mx+3≥0的解集为R,求实数m的取值范围.
19.已知数列{an}是等差数列,其前n项和为Sn,且a3=6,S3=12,设.
(1)求an;
(2)求数列{bn}的前n项和Tn.
20.如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,PA=AB=BC=2,AD=4.
(1)求四棱锥P﹣ABCD的体积;
(2)求证:CD⊥平面PAC.
21.△ABC中,角A,B,C的对边分别为a,b,c,已知.
(Ⅰ)求角B的大小;
(Ⅱ)点D为边AB上的一点,记∠BDC=θ,若<θ<π,CD=2,,a=,求sinθ与b的值.
22.已知圆C:(x﹣3)2+(y﹣4)2=4,直线l1过定点A
(1,0).
(Ⅰ)若l1与圆C相切,求l1的方程;
(Ⅱ)若l1与圆C相交于P,Q两点,求三角形CPQ的面积的最大值,并求此时直线l1的方程.
2016-2017学年湖南省张家界市高一(下)期末数学试卷(B卷)
参考答案与试题解析
一、选择题:本大题共12小题,每小题5分,满分60分.
1.1和5的等差中项是( )
A.
B.
C.3
D.±3
【考点】84:等差数列的通项公式.
【分析】由a,b,c成等差数列,可得2b=a+c,计算即可得到所求值.
【解答】解:1和5的等差中项为=3,
故选:C.
2.设a>b,则下列不等式中正确的是( )
A.
B.a+c>b+c
C.ac2>bc2
D.a2>b2
【考点】R3:不等式的基本性质.
【分析】根据题意,依次分析四个选项中的不等式,综合即可得答案.
【解答】解:根据题意,依次分析选项:
对于A,当a=2,b=1时,有<,故A错误;
对于B、不等式两边加(或减)同一个数(或式子),不等号的方向不变,故B正确;
对于C、当c=0时,ac2=bc2,故C错误;
对于D、当a=1,b=﹣2时,a2=1,b2=4,此时a2<b2,故D错误;
故选:B.
3.直线l经过原点O和点P(1,1),则其斜率为( )
A.1
B.﹣1
C.﹣2
D.2
【考点】I3:直线的斜率.
【分析】根据题意,由直线斜率的计算公式直接计算即可得答案.
【解答】解:根据题意,直线l经过原点O和点P(1,1),
则其斜率k==1;
故选:A.
4.下列结论中正确的是( )
A.经过三点确定一个平面
B.平行于同一平面的两条直线平行
C.垂直于同一直线的两条直线平行
D.垂直于同一平面的两条直线平行
【考点】LP:空间中直线与平面之间的位置关系.
【分析】A,经过不共线的三点才可以确定一个平面,
B,平行于同一平面的两条直线可能平行、相交、异面;
C,垂直于同一直线的两条直线可能平行、相交、异面;
D,根据直线与平面垂直的性质定理直接可得答案,
【解答】解:对于A,经过不共线的三点才可以确定一个平面,故错,
对于B,平行于同一平面的两条直线可能平行、相交、异面,故错;
对于C,垂直于同一直线的两条直线可能平行、相交、异面,故错;
对于D,根据直线与平面垂直的性质定理,可得垂直于同一平面的两条直线平行,故正确.
故选:D
5.空间两点A(1,2,﹣2),B(﹣1,0,﹣1)之间的距离为( )
A.5
B.3
C.2
D.1
【考点】JI:空间两点间的距离公式.
【分析】根据空间中两点间的距离公式计算即可.
【解答】解:空间两点A(1,2,﹣2),B(﹣1,0,﹣1)之间的距离为
|AB|==3.
故选:B.
6.如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是( )
A.6
B.3
C.12
D.6
【考点】LD:斜二测法画直观图.
【分析】画出△OAB的直观图,根据数据求出直观图的面积.
【解答】解:△O′A′B′是水平放置的△OAB的直观图,
所以:S△OAB==12
故选C.
7.在△ABC中,面积,c=2,B=60°,则a=( )
A.2
B.
C.
D.1
【考点】HT:三角形中的几何计算.
【分析】利用,能求出a.
【解答】解:在△ABC中,
∵面积,c=2,B=60°,
∴,即,
解得a=1.
故选:D.
8.圆x2+y2=4与圆(x﹣3)2+y2=1的位置关系为( )
A.内切
B.相交
C.外切
D.相离
【考点】JA:圆与圆的位置关系及其判定.
【分析】根据题意,由两圆的标准方程分析可得两圆的圆心与半径,分析计算两圆的圆心距与半径和之间的关系,即可得答案.
【解答】解:根据题意,设圆x2+y2=4的圆心为M,半径为r1,则M(0,0),r1=2,
圆(x﹣3)2+y2=1的圆心为N,半径为r2,N(3,0),r2=1,
则有|MN|=r1+r2=3,
则两圆外切;
故选:C.
9.已知一个几何体的三视图如图所示,则该几何体的体积为( )
A.4π
B.6π
C.8π
D.16π
【考点】L!:由三视图求面积、体积.
【分析】由三视图还原原几何体,可知原几何体是底面半径为1,高为4的圆柱,再由圆柱体积公式得答案.
【解答】解:由三视图还原原几何体如图:
该几何体是底面半径为1,高为4的圆柱,
则其体积为π×12×4=4π.
故选:A.
10.设x,y满足如图所示的可行域(阴影部分),则的最大值为( )
A.
B.0
C.
D.﹣1
【考点】7C:简单线性规划.
【分析】把目标函数化为y=x﹣z,平移直线y=x﹣z找出最优解,求出目标函数的最大值.
【解答】解:x,y满足如图所示的可行域(阴影部分),
则目标函数可化为y=x﹣z,
平移直线y=x﹣z,
当直线y=x﹣z过点A(1,0)时,
z取得最大值为zmax=×1﹣0=.
故选:A.
11.《九章算术》是我国古代内容极为丰富的一部数学专著,书中有如下问题:今有女子善织,日增等尺,七日织28尺,第二日,第五日,第八日所织之和为15尺,则第九日所织尺数为( )
A.8
B.9
C.10
D.11
【考点】84:等差数列的通项公式.
【分析】由题意可知,每日所织数量构成等差数列,再由已知求得a5,a4的值,进一步求得公差,代入等差数列的通项公式求得第九日所织尺数.
【解答】解:由题意可知,每日所织数量构成等差数列,且a2+a5+a8=15,S7=28,
设公差为d,由a2+a5+a8=15,得3a5=15,∴a5=5,
由S7=28,得7a4=28,∴a4=4,则d=a5﹣a4=1,
∴a9=a5+4d=5+4×1=9.
故选:B.
12.设x∈R,记不超过x的最大整数为[x],令{x}=x﹣[x],则{},[],( )
A.是等差数列但不是等比数列
B.是等比数列但不是等差数列
C.既是等差数列又是等比数列
D.既不是等差数列也不是等比数列
【考点】8C:等差关系的确定;8D:等比关系的确定.
【分析】可分别求得,.则等比数列性质易得三者构成等比数列.
【解答】解:根据题意可得,.
∵×=12,
+≠2
∴{},[],为等比数列,不是等差数列
故选B.
二、填空题:本大题共4小题,每小题5分,满分20分.
13.若x>1,则x+的最小值是 3 .
【考点】7F:基本不等式.
【分析】x+=x﹣1++1,利用基本不等式可求函数的最值.
【解答】解:∵x>1,
∴x+=x﹣1++1+1=3,
当且仅当x﹣1=即x=2时取等号,
∴x=2时x+取得最小值3,
故答案为:3.
14.若直线y=kx+2与直线y=2x﹣1互相平行,则实数k= 2 .
【考点】II:直线的一般式方程与直线的平行关系.
【分析】利用直线平行的性质直接求解.
【解答】解:∵直线y=kx+2与直线y=2x﹣1互相平行,
∴实数k=2.
故答案为:2.
15.表面积为4π的球的半径为 1 .
【考点】LG:球的体积和表面积.
【分析】由球的表面积公式S=4πR2,直接计算.
【解答】解:设球的半径为R,由球的表面积公式S=4πR2=4π,解得R=1.
故答案为:1
16.△ABC的三边a,b,c成等比数列,则角B的范围是 0<B≤ .
【考点】8B:数列的应用.
【分析】根据题中已知条件求出a,b,c之间的关系,然后利用余弦定理便可求出cosB的值,即可求出角B的范围.
【解答】解:由题意知:a,b,c成等比数列,
∴b2=ac,
又∵a,b,c是三角形的三边,不妨设a≤b≤c,
由余弦定理得
故有,
故答案为.
三、解答题:本大题共6小题,满分70分.解答应写出文字说明、证明过程或演算步骤.
17.已知直线l1:3x+4y﹣2=0,l2:2x+y+2=0相交于点P.
(1)求点P的坐标;
(2)求过点P且与直线x﹣2y﹣1=0垂直的直线l的方程.
【考点】IK:待定系数法求直线方程;IM:两条直线的交点坐标.
【分析】(1)把两条直线的方程联立方程组,求得该方程组的解,即可求得交点P的坐标.
(2)利用两条直线垂直的性质求得直线l的斜率,再用点斜式求出直线l的方程.
【解答】(1)由,求得,∴两条直线的交点坐标为
P(﹣2,2).
(2)直线x﹣2y﹣1=0的斜率为,故要求的直线l的斜率为﹣2,故要求的直线的方程为y﹣2=﹣2(x+2),
即直线l的方程为2x+y+2=0.
18.已知不等式(1﹣a)x2﹣4x+6>0的解集为{x|﹣3<x<1}.
(1)求a的值;
(2)若不等式ax2+mx+3≥0的解集为R,求实数m的取值范围.
【考点】74:一元二次不等式的解法.
【分析】(1)一元二次不等式与对应方程的关系,旅游根与系数的关系求出a的值;
(2)根据一元二次不等式解集为R,利用判别式△≤0,求出m的取值范围.
【解答】解:(1)不等式(1﹣a)x2﹣4x+6>0的解集为{x|﹣3<x<1},
∴1﹣a<0,且方程(1﹣a)x2﹣4x+6=0的两根为﹣3,1;
由根与系数的关系知,
解得a=3;…
(2)不等式3x2+mx+3≥0的解集为R,
则△=m2﹣4×3×3≤0,
解得﹣6≤m≤6,
∴实数m的取值范围为(﹣6,6).…
19.已知数列{an}是等差数列,其前n项和为Sn,且a3=6,S3=12,设.
(1)求an;
(2)求数列{bn}的前n项和Tn.
【考点】8E:数列的求和;8H:数列递推式.
【分析】(1)设数列{an}是公差为d的等差数列,运用等差数列的通项公式和求和公式,解方程可得首项和公差,即可得到所求通项;
(2)求出=4n,运用等比数列的求和公式,化简计算即可得到所求和.
【解答】解:(1)设数列{an}是公差为d的等差数列,
;
(2),
可得Tn=b1+b2+b3+…+bn=4+42+43+…+4n
=.
20.如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,PA=AB=BC=2,AD=4.
(1)求四棱锥P﹣ABCD的体积;
(2)求证:CD⊥平面PAC.
【考点】LF:棱柱、棱锥、棱台的体积;LW:直线与平面垂直的判定.
【分析】(1)由四边形ABCD是直角梯形,PA⊥底面ABCD,能求出四棱锥P﹣ABCD的体积.
(2)由PA⊥底面ABCD,得PA⊥CD,由勾股定理得AC⊥CD,由此能证明CD⊥平面PAC.
【解答】解:(1)由已知,四边形ABCD是直角梯形,
∴,
∵PA⊥底面ABCD,
∴四棱锥P﹣ABCD的体积.…
证明:(2)由PA⊥底面ABCD,CD 底面ABCD,则PA⊥CD,
在三角形ABC中,,
又,∴AC2+CD2=AD2,即AC⊥CD,…
又∵PA,AC 平面PAC,PA∩AC=A,
∴CD⊥平面PAC.…
21.△ABC中,角A,B,C的对边分别为a,b,c,已知.
(Ⅰ)求角B的大小;
(Ⅱ)点D为边AB上的一点,记∠BDC=θ,若<θ<π,CD=2,,a=,求sinθ与b的值.
【考点】HR:余弦定理;HP:正弦定理.
【分析】(Ⅰ)由正弦定理,同角三角函数基本关系式化简已知等式可得tanB=,结合范围0<B<π,可求B的值.
(Ⅱ)在△BCD中,由正弦定理可得=,解得sinθ=,结合θ为钝角,利用诱导公式可求cos∠ADC的值,在△ADC中,由余弦定理,可得b的值.
【解答】(本题满分为12分)
解:(Ⅰ)∵,∴可得:,
∵sinC>0,∴
=tanB=,
∵0<B<π,
∴B=…4分
(Ⅱ)在△BCD中,∵
=,
∴=,∴sinθ=,…8分
∵θ为钝角,
∴∠ADC为锐角,
∴cos∠ADC=cos(π﹣θ)==,
∴在△ADC中,由余弦定理,可得:
b===…12分
22.已知圆C:(x﹣3)2+(y﹣4)2=4,直线l1过定点A
(1,0).
(Ⅰ)若l1与圆C相切,求l1的方程;
(Ⅱ)若l1与圆C相交于P,Q两点,求三角形CPQ的面积的最大值,并求此时直线l1的方程.
【考点】J7:圆的切线方程;IT:点到直线的距离公式.
【分析】(Ⅰ)通过直线l1的斜率存在与不存在两种情况,利用直线的方程与圆C相切,圆心到直线的距离等于半径,即可求l1的方程;
(Ⅱ)设直线方程为kx﹣y﹣k=0,求出圆心到直线的距离,弦长,得到三角形CPQ的面积的表达式,利用二次函数求出面积的最大值时的距离,然后求出直线的斜率,即可得到l1的直线方程.
【解答】解:(Ⅰ)
①若直线l1的斜率不存在,则直线l1:x=1,符合题意.
②若直线l1斜率存在,设直线l1的方程为y=k(x﹣1),即kx﹣y﹣k=0.
由题意知,圆心(3,4)到已知直线l1的距离等于半径2,
即:,解之得.
所求直线l1的方程是x=1或3x﹣4y﹣3=0.
(Ⅱ)直线与圆相交,斜率必定存在,且不为0,设直线方程为kx﹣y﹣k=0,
则圆心到直l1的距离d=
又∵三角形CPQ面积S=×2=d=
∴当d=时,S取得最大值2.
∴d==,k=1或k=7.
∴直线方程为y=x﹣1,或y=7x﹣7.
同课章节目录
