八年级数学上册第一章勾股定理3勾股定理的应用中考考点链接学案(新版)北师大版
文档属性
| 名称 | 八年级数学上册第一章勾股定理3勾股定理的应用中考考点链接学案(新版)北师大版 | 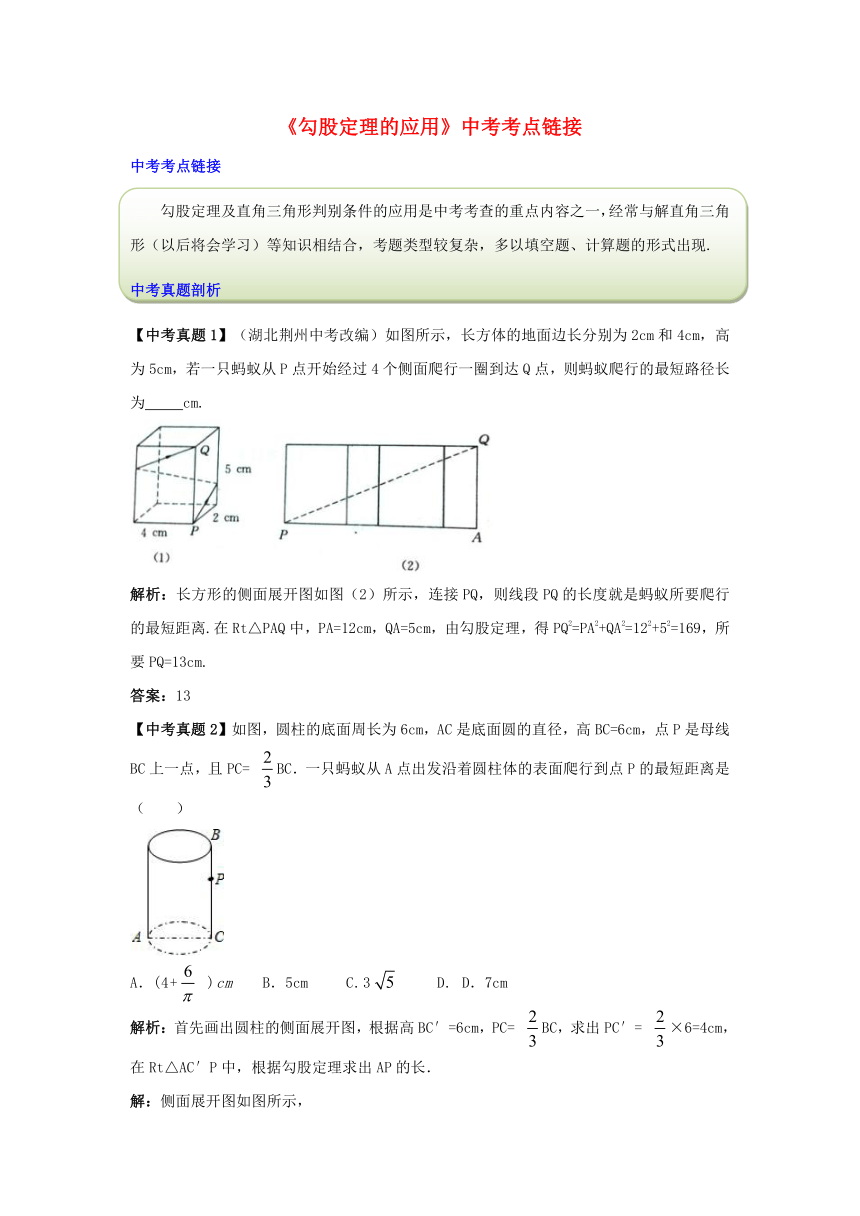 | |
| 格式 | zip | ||
| 文件大小 | 216.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-23 19:42:08 | ||
图片预览


文档简介
《勾股定理的应用》中考考点链接
中考考点链接
勾股定理及直角三角形判别条件的应用是中考考查的重点内容之一,经常与解直角三角形(以后将会学习)等知识相结合,考题类型较复杂,多以填空题、计算题的形式出现.
中考真题剖析
【中考真题1】(湖北荆州中考改编)如图所示,长方体的地面边长分别为2cm和4cm,高为5cm,若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为
cm.
解析:长方形的侧面展开图如图(2)所示,连接PQ,则线段PQ的长度就是蚂蚁所要爬行的最短距离.在Rt△PAQ中,PA=12cm,QA=5cm,由勾股定理,得PQ2=PA2+QA2=122+52=169,所要PQ=13cm.
答案:13
【中考真题2】如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC=
BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
A.(4+
)cm
B.5cm
C.3
D.
D.7cm
解析:首先画出圆柱的侧面展开图,根据高BC′=6cm,PC=
BC,求出PC′=
×6=4cm,在Rt△AC′P中,根据勾股定理求出AP的长.
解:侧面展开图如图所示,
∵圆柱的底面周长为6cm,
∴AC′=3cm,
∵PC′=BC′,
∴PC′=×6=4cm,
在Rt△ACP中,
AP2=AC′2+CP2
∴AP==5.
故选B
【对接点】教材第15页习题1.4第4题.
【考题点睛】中考题与教材习题都是长方体表面上两点之间最短距离的问题,解题的思路、方法相同,都是把立体图形问题转化为求平面上两点之间距离的问题,一般都是运用勾股定理求解.
中考真题演练
1.
(济南)如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度为(滑轮上方的部分忽略不计)为( )
A.12m
B.13m
C.16m
D.17m
2.
(安顺)如图,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,问小鸟至少飞行( )
A.8米
B.10米
C.12米
D.14米
3.
(乐山)如图,一圆锥的底面半径为2,母线PB的长为6,D为PB的中点.一只蚂蚁从点A出发,沿着圆锥的侧面爬行到点D,则蚂蚁爬行的最短路程为( )
A.
B.2
C.3
D.
参考答案
1.
分析:根据题意画出示意图,设旗杆高度为x,可得AC=AD=x,AB=(x-2)m,BC=8m,在Rt△ABC中利用勾股定理可求出x.
解:设旗杆高度为x,则AC=AD=x,AB=(x-2)m,BC=8m,
在Rt△ABC中,AB2+BC2=AC2,即(x-2)2+82=x2,
解得:x=17,
即旗杆的高度为17米.
故选:D.
2.分析:根据“两点之间线段最短”可知:小鸟沿着两棵树的树梢进行直线飞行,所行的路程最短,运用勾股定理可将两点之间的距离求出.
解:如图,设大树高为AB=10m,
小树高为CD=4m,
过C点作CE⊥AB于E,则EBDC是矩形,
连接AC,
∴EB=4m,EC=8m,AE=AB-EB=10-4=6m,
在Rt△AEC中,AC==10m,
故选B.
3.分析:要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果.
中考考点链接
勾股定理及直角三角形判别条件的应用是中考考查的重点内容之一,经常与解直角三角形(以后将会学习)等知识相结合,考题类型较复杂,多以填空题、计算题的形式出现.
中考真题剖析
【中考真题1】(湖北荆州中考改编)如图所示,长方体的地面边长分别为2cm和4cm,高为5cm,若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为
cm.
解析:长方形的侧面展开图如图(2)所示,连接PQ,则线段PQ的长度就是蚂蚁所要爬行的最短距离.在Rt△PAQ中,PA=12cm,QA=5cm,由勾股定理,得PQ2=PA2+QA2=122+52=169,所要PQ=13cm.
答案:13
【中考真题2】如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC=
BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
A.(4+
)cm
B.5cm
C.3
D.
D.7cm
解析:首先画出圆柱的侧面展开图,根据高BC′=6cm,PC=
BC,求出PC′=
×6=4cm,在Rt△AC′P中,根据勾股定理求出AP的长.
解:侧面展开图如图所示,
∵圆柱的底面周长为6cm,
∴AC′=3cm,
∵PC′=BC′,
∴PC′=×6=4cm,
在Rt△ACP中,
AP2=AC′2+CP2
∴AP==5.
故选B
【对接点】教材第15页习题1.4第4题.
【考题点睛】中考题与教材习题都是长方体表面上两点之间最短距离的问题,解题的思路、方法相同,都是把立体图形问题转化为求平面上两点之间距离的问题,一般都是运用勾股定理求解.
中考真题演练
1.
(济南)如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度为(滑轮上方的部分忽略不计)为( )
A.12m
B.13m
C.16m
D.17m
2.
(安顺)如图,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,问小鸟至少飞行( )
A.8米
B.10米
C.12米
D.14米
3.
(乐山)如图,一圆锥的底面半径为2,母线PB的长为6,D为PB的中点.一只蚂蚁从点A出发,沿着圆锥的侧面爬行到点D,则蚂蚁爬行的最短路程为( )
A.
B.2
C.3
D.
参考答案
1.
分析:根据题意画出示意图,设旗杆高度为x,可得AC=AD=x,AB=(x-2)m,BC=8m,在Rt△ABC中利用勾股定理可求出x.
解:设旗杆高度为x,则AC=AD=x,AB=(x-2)m,BC=8m,
在Rt△ABC中,AB2+BC2=AC2,即(x-2)2+82=x2,
解得:x=17,
即旗杆的高度为17米.
故选:D.
2.分析:根据“两点之间线段最短”可知:小鸟沿着两棵树的树梢进行直线飞行,所行的路程最短,运用勾股定理可将两点之间的距离求出.
解:如图,设大树高为AB=10m,
小树高为CD=4m,
过C点作CE⊥AB于E,则EBDC是矩形,
连接AC,
∴EB=4m,EC=8m,AE=AB-EB=10-4=6m,
在Rt△AEC中,AC==10m,
故选B.
3.分析:要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
