七年级数学上册5.1丰富的图形世界考题聚焦学案(新版)苏科版
文档属性
| 名称 | 七年级数学上册5.1丰富的图形世界考题聚焦学案(新版)苏科版 |
|
|
| 格式 | zip | ||
| 文件大小 | 127.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-23 19:47:02 | ||
图片预览

文档简介
丰富的图形世界
我们生活的空间存在着大量的图形.利用直观图形可以帮助我们更好地理解自然和社会.以丰富的图形为情境设计问题,成为近年中考的热点题型.要解决这类问题,除了认真观察分析图形或动手实际操作外,还应充分发挥空间想象能力.下面从各地中考及竞赛题中选取几类与图形有关的题目,供同学们学习时参考.
一、几何体的表面展开图
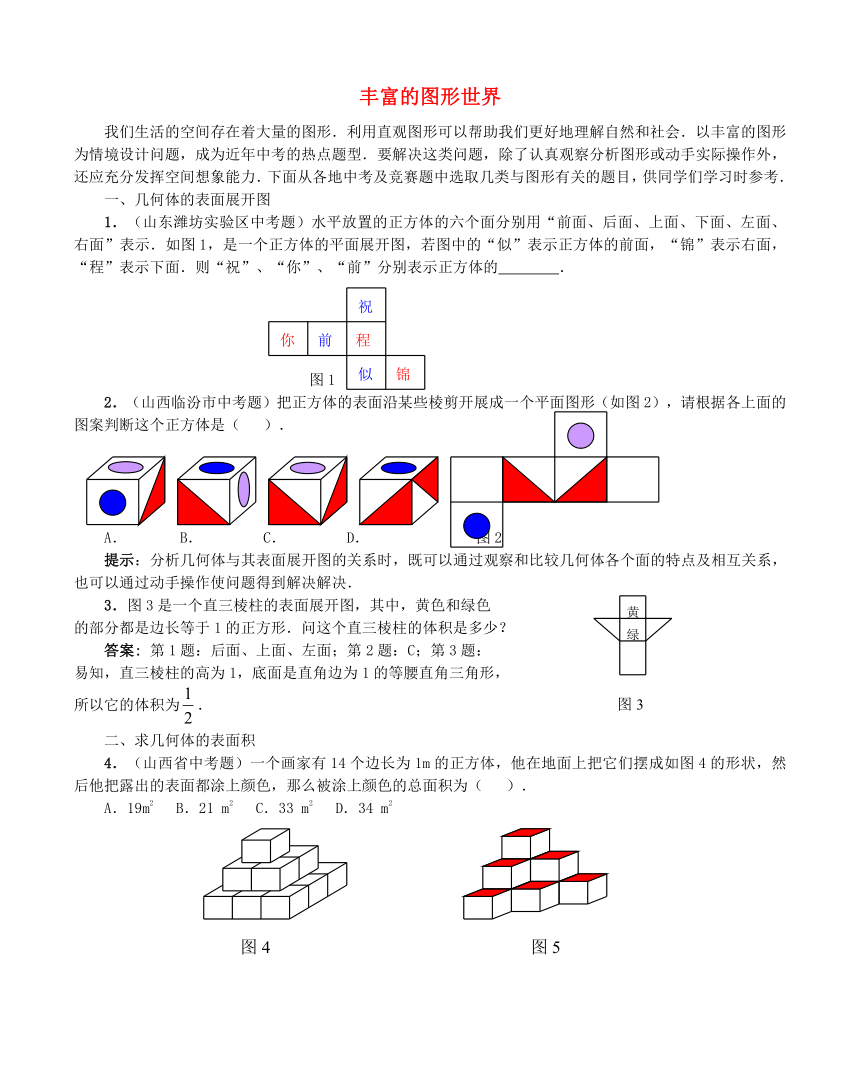
1.(山东潍坊实验区中考题)水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如图1,是一个正方体的平面展开图,若图中的“似”表示正方体的前面,“锦”表示右面,“程”表示下面.则“祝”、“你”、“前”分别表示正方体的
.
图1
2.(山西临汾市中考题)把正方体的表面沿某些棱剪开展成一个平面图形(如图2),请根据各上面的图案判断这个正方体是(
).
A.
B.
C.
D.
图2
提示:分析几何体与其表面展开图的关系时,既可以通过观察和比较几何体各个面的特点及相互关系,也可以通过动手操作使问题得到解决解决.
3.图3是一个直三棱柱的表面展开图,其中,黄色和绿色
的部分都是边长等于1的正方形.问这个直三棱柱的体积是多少?
答案:
第1题:后面、上面、左面;第2题:C;第3题:
易知,直三棱柱的高为1,底面是直角边为1的等腰直角三角形,
所以它的体积为.
二、求几何体的表面积
4.(山西省中考题)一个画家有14个边长为1m的正方体,他在地面上把它们摆成如图4的形状,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为(
).
A.19m2
B.21
m2
C.33
m2
D.34
m2
5.(贵阳市实验区中考题)棱长是1cm的小立方体组成如图5所示的几何体,那么这个几何体的表面积是(
).
A.36cm2
B.33cm2
C.30cm2
D.27cm2
提示:在分析几何体的表面积时,要注意弄清哪些面露在外面,哪些面盖在里面.
答案:第4题:C;第5题:A.
三、推理问题
6.(山东威海市中考题)立方体木块的六个面分别标有数字1、2、3、4、5、6,图6是从不同方向观察这个立方体木块看到的数字情况,数字1和5对面的数字的和是
.
①
②
③
提示:本题主要考查空间想象能力和推理能力.由图①可知,标有数字1、2、5的三个面相邻,所以再由图②可知,数字4对面的数字是5;由图③可知,标有数字1、4、6的三个面相邻,所以再结合图②可知,数字2对面的数字是6.所以数字1的对面是3.由此不难得出结果为3+4=7.
四、多边形的分割
7.(广东省中考题)阅读材料:
多边形边上或内部的一点与多边形各顶点的连线,将多边形分割成若干个小三角形.图7给出了四边形的具体分割方法,分别将四边形分成了2个、3个、4个小三角形.
请你按照上述方法将图8中的六边形进行分割,并写出得到的小三角形的个数.试把这一结论推广至n边形.
①
②
③
图7
①
②
③
图8
提示:这是一个阅读理解型问题,通过模拟阅读材料中所提供的方法即可解决.
答案:①连接六边形一个顶点和其他各顶点,共分成了4个三角形;
②连接六边形某一边上一点和各顶点,共分成了5个三角形;
③连接六边形内一点和各顶点,共分成了6个三角形(画图略).
推广结论至n边形,分割后得到的小三角形的个数分别为n—2,n—1,n.
五、几何体的视图
8.(贵阳市实验区中考题)由一些大小相同的小正方体组成的简单几何体的主视图和俯视图(如图9).
①请你画出这个几何体的一种左视图;
②若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
图9
提示:这是一道探索结论的开放性试题.需要由所给出的视图,想象出这个几何体各种不同的情况,进而得出完整、正确的结论.
答案:①左视图有以下5种情况:
②n=8,9,10,11.
似
锦
你
前
程
祝
黄
绿
图3
图5
图4
2
5
1
2
1
4
4
1
6
图图6
俯视图
主视图
我们生活的空间存在着大量的图形.利用直观图形可以帮助我们更好地理解自然和社会.以丰富的图形为情境设计问题,成为近年中考的热点题型.要解决这类问题,除了认真观察分析图形或动手实际操作外,还应充分发挥空间想象能力.下面从各地中考及竞赛题中选取几类与图形有关的题目,供同学们学习时参考.
一、几何体的表面展开图
1.(山东潍坊实验区中考题)水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如图1,是一个正方体的平面展开图,若图中的“似”表示正方体的前面,“锦”表示右面,“程”表示下面.则“祝”、“你”、“前”分别表示正方体的
.
图1
2.(山西临汾市中考题)把正方体的表面沿某些棱剪开展成一个平面图形(如图2),请根据各上面的图案判断这个正方体是(
).
A.
B.
C.
D.
图2
提示:分析几何体与其表面展开图的关系时,既可以通过观察和比较几何体各个面的特点及相互关系,也可以通过动手操作使问题得到解决解决.
3.图3是一个直三棱柱的表面展开图,其中,黄色和绿色
的部分都是边长等于1的正方形.问这个直三棱柱的体积是多少?
答案:
第1题:后面、上面、左面;第2题:C;第3题:
易知,直三棱柱的高为1,底面是直角边为1的等腰直角三角形,
所以它的体积为.
二、求几何体的表面积
4.(山西省中考题)一个画家有14个边长为1m的正方体,他在地面上把它们摆成如图4的形状,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为(
).
A.19m2
B.21
m2
C.33
m2
D.34
m2
5.(贵阳市实验区中考题)棱长是1cm的小立方体组成如图5所示的几何体,那么这个几何体的表面积是(
).
A.36cm2
B.33cm2
C.30cm2
D.27cm2
提示:在分析几何体的表面积时,要注意弄清哪些面露在外面,哪些面盖在里面.
答案:第4题:C;第5题:A.
三、推理问题
6.(山东威海市中考题)立方体木块的六个面分别标有数字1、2、3、4、5、6,图6是从不同方向观察这个立方体木块看到的数字情况,数字1和5对面的数字的和是
.
①
②
③
提示:本题主要考查空间想象能力和推理能力.由图①可知,标有数字1、2、5的三个面相邻,所以再由图②可知,数字4对面的数字是5;由图③可知,标有数字1、4、6的三个面相邻,所以再结合图②可知,数字2对面的数字是6.所以数字1的对面是3.由此不难得出结果为3+4=7.
四、多边形的分割
7.(广东省中考题)阅读材料:
多边形边上或内部的一点与多边形各顶点的连线,将多边形分割成若干个小三角形.图7给出了四边形的具体分割方法,分别将四边形分成了2个、3个、4个小三角形.
请你按照上述方法将图8中的六边形进行分割,并写出得到的小三角形的个数.试把这一结论推广至n边形.
①
②
③
图7
①
②
③
图8
提示:这是一个阅读理解型问题,通过模拟阅读材料中所提供的方法即可解决.
答案:①连接六边形一个顶点和其他各顶点,共分成了4个三角形;
②连接六边形某一边上一点和各顶点,共分成了5个三角形;
③连接六边形内一点和各顶点,共分成了6个三角形(画图略).
推广结论至n边形,分割后得到的小三角形的个数分别为n—2,n—1,n.
五、几何体的视图
8.(贵阳市实验区中考题)由一些大小相同的小正方体组成的简单几何体的主视图和俯视图(如图9).
①请你画出这个几何体的一种左视图;
②若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
图9
提示:这是一道探索结论的开放性试题.需要由所给出的视图,想象出这个几何体各种不同的情况,进而得出完整、正确的结论.
答案:①左视图有以下5种情况:
②n=8,9,10,11.
似
锦
你
前
程
祝
黄
绿
图3
图5
图4
2
5
1
2
1
4
4
1
6
图图6
俯视图
主视图
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
