圆中的计算问题练习题(有答案)
图片预览


文档简介
圆中的计算问题
练习题
一、选择题
1、圆心角为45°,直径为4cm的扇形的弧长是(
)cm.
A、
B、
C、
D、
2、圆心角为120°,半径为3cm的扇形的面积是(
)cm2;
A、
B、
C、
D、
3、弧长为4,半径为3的扇形的面积是(
)
A、
B、
C、12
D、6
4、如图,正方形ABCD的边AB=1,和都是以1为半径的圆弧,则无阴影两部分的面积之差是( )
A.
B.1﹣
C.﹣1
D.
1﹣
5、在半径为2的圆中,弦AB的长为2,则的长等于( )
A.
B.
C.
D.
6、如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,则点B在两次旋转过程中经过的路径的长是( )
A.
B.13π
C.25π
D.
25
7、如果圆锥的母线长为5cm,底面半径为2cm,那么这个圆锥的侧面积为( )
A.
10cm2
B.10πcm2
C.20cm2
D.
20πcm2
8、已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的圆心角是( )
A.
30°
B.60°
C.90°
D.
180°
二、填空题
1、圆锥的底面半径为6cm,母线长为10cm,则圆锥的侧面积为
cm2.
2、圆锥的底面半径是2cm,母线长6cm,则这个圆锥侧面展开图的扇形圆心角度数 度.
3、若扇形的圆心角为60°,弧长为2π,则扇形的半径为
.
4、如图,正三角形ABC的边长为2,点A,B在半径为的圆上,点C在圆内,将正三角形ABC绕点A逆时针旋转,当点C第一次落在圆上时,点C运动的路线长是 .
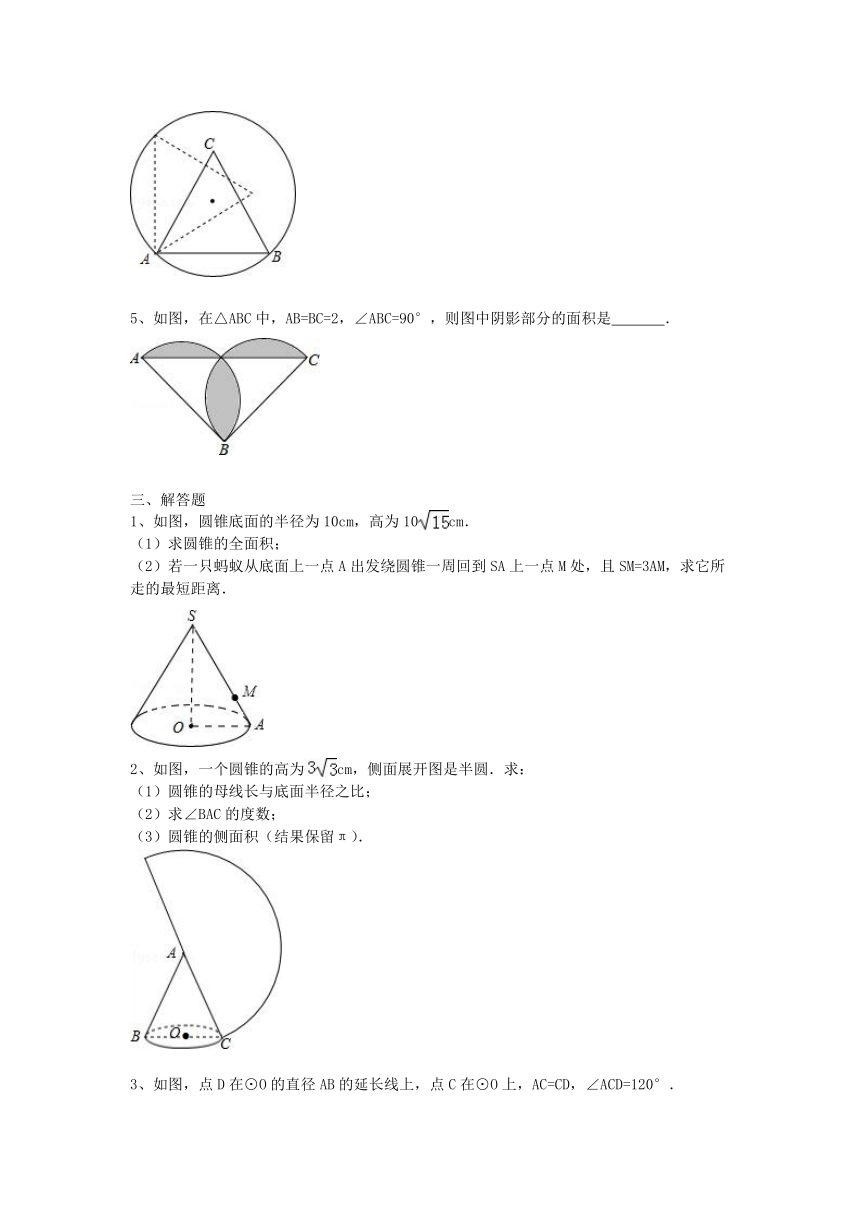
5、如图,在△ABC中,AB=BC=2,∠ABC=90°,则图中阴影部分的面积是
.
三、解答题
1、如图,圆锥底面的半径为10cm,高为10cm.
(1)求圆锥的全面积;
(2)若一只蚂蚁从底面上一点A出发绕圆锥一周回到SA上一点M处,且SM=3AM,求它所走的最短距离.
2、如图,一个圆锥的高为cm,侧面展开图是半圆.求:
(1)圆锥的母线长与底面半径之比;
(2)求∠BAC的度数;
(3)圆锥的侧面积(结果保留π).
3、如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
4、如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,OC=2,求阴影部分图形的面积(结果保留π).
5、如图,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2.
(1)求线段EC的长;
(2)求图中阴影部分的面积.
圆中的计算问题练习题答案
一、选择题
ACDAC
ABD
二、填空题
1、60
2、120
3、6
4、
5、
三、解答题
1、解:(1)由题意,可得圆锥的母线SA==40(cm)
圆锥的侧面展开扇形的弧长l=2π OA=20πcm
∴S侧=L SA=400πcm2
S圆=πAO2=100πcm2,
∴S全=S圆+S底=(400+100)π=500π(cm2);
(2)沿母线SA将圆锥的侧面展开,如右图,则线段AM的长就是蚂蚁所走的最短距离
由(1)知,SA=40cm,弧AA′=20πcm
∵=20πcm,
∴∠S=n==90°,
∵SA′=SA=40cm,SM=3A′M
∴SM=30cm,
∴在Rt△ASM中,由勾股定理得AM=50(cm)
所以,蚂蚁所走的最短距离是50cm.
2、解:(1)设此圆锥的高为h,底面半径为r,母线长AC=l,
∵2πr=πl,
∴l:r=2:1;
(2)∵AO⊥OC,=2,
∴圆锥高与母线的夹角为30°,
则∠BAC=60°;
(3)由图可知l2=h2+r2,h=3cm,
∴(2r)2=(3)2+r2,即4r2=27+r2,
解得r=3cm,
∴l=2r=6cm,
∴圆锥的侧面积为=18π(cm2).
3、(1)证明:连接OC.
∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠2=∠A=30°.
∴∠OCD=180°﹣∠A﹣∠D﹣∠2=90°.
∴CD是⊙O的切线.
(2)解:∵∠A=30°,
∴∠1=2∠A=60°.
∴S扇形BOC=.
在Rt△OCD中,
∵,
∴.
∴.
∴图中阴影部分的面积为:.
4、解:∵AB是⊙O的直径,弦CD⊥AB于点E,
∴CE=DE,∠CEO=∠DEB=90°.
∵∠CDB=30°,
∴∠COB=60°,∠OCE=∠CDB,
在△OCE和△BDE中,
∵,
∴△OCE≌△BDE,
∴S阴影=S扇形OCB==π.
5、解:(1)∵在矩形ABCD中,AB=2DA,DA=2,
∴AB=AE=4,
∴DE==2,
∴EC=CD﹣DE=4﹣2;
(2)∵sin∠DEA==,
∴∠DEA=30°,
∴∠EAB=30°,
∴图中阴影部分的面积为:
S扇形FAB﹣S△DAE﹣S扇形EAB
=﹣×2×2﹣
=﹣2.
练习题
一、选择题
1、圆心角为45°,直径为4cm的扇形的弧长是(
)cm.
A、
B、
C、
D、
2、圆心角为120°,半径为3cm的扇形的面积是(
)cm2;
A、
B、
C、
D、
3、弧长为4,半径为3的扇形的面积是(
)
A、
B、
C、12
D、6
4、如图,正方形ABCD的边AB=1,和都是以1为半径的圆弧,则无阴影两部分的面积之差是( )
A.
B.1﹣
C.﹣1
D.
1﹣
5、在半径为2的圆中,弦AB的长为2,则的长等于( )
A.
B.
C.
D.
6、如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,则点B在两次旋转过程中经过的路径的长是( )
A.
B.13π
C.25π
D.
25
7、如果圆锥的母线长为5cm,底面半径为2cm,那么这个圆锥的侧面积为( )
A.
10cm2
B.10πcm2
C.20cm2
D.
20πcm2
8、已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的圆心角是( )
A.
30°
B.60°
C.90°
D.
180°
二、填空题
1、圆锥的底面半径为6cm,母线长为10cm,则圆锥的侧面积为
cm2.
2、圆锥的底面半径是2cm,母线长6cm,则这个圆锥侧面展开图的扇形圆心角度数 度.
3、若扇形的圆心角为60°,弧长为2π,则扇形的半径为
.
4、如图,正三角形ABC的边长为2,点A,B在半径为的圆上,点C在圆内,将正三角形ABC绕点A逆时针旋转,当点C第一次落在圆上时,点C运动的路线长是 .
5、如图,在△ABC中,AB=BC=2,∠ABC=90°,则图中阴影部分的面积是
.
三、解答题
1、如图,圆锥底面的半径为10cm,高为10cm.
(1)求圆锥的全面积;
(2)若一只蚂蚁从底面上一点A出发绕圆锥一周回到SA上一点M处,且SM=3AM,求它所走的最短距离.
2、如图,一个圆锥的高为cm,侧面展开图是半圆.求:
(1)圆锥的母线长与底面半径之比;
(2)求∠BAC的度数;
(3)圆锥的侧面积(结果保留π).
3、如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
4、如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,OC=2,求阴影部分图形的面积(结果保留π).
5、如图,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2.
(1)求线段EC的长;
(2)求图中阴影部分的面积.
圆中的计算问题练习题答案
一、选择题
ACDAC
ABD
二、填空题
1、60
2、120
3、6
4、
5、
三、解答题
1、解:(1)由题意,可得圆锥的母线SA==40(cm)
圆锥的侧面展开扇形的弧长l=2π OA=20πcm
∴S侧=L SA=400πcm2
S圆=πAO2=100πcm2,
∴S全=S圆+S底=(400+100)π=500π(cm2);
(2)沿母线SA将圆锥的侧面展开,如右图,则线段AM的长就是蚂蚁所走的最短距离
由(1)知,SA=40cm,弧AA′=20πcm
∵=20πcm,
∴∠S=n==90°,
∵SA′=SA=40cm,SM=3A′M
∴SM=30cm,
∴在Rt△ASM中,由勾股定理得AM=50(cm)
所以,蚂蚁所走的最短距离是50cm.
2、解:(1)设此圆锥的高为h,底面半径为r,母线长AC=l,
∵2πr=πl,
∴l:r=2:1;
(2)∵AO⊥OC,=2,
∴圆锥高与母线的夹角为30°,
则∠BAC=60°;
(3)由图可知l2=h2+r2,h=3cm,
∴(2r)2=(3)2+r2,即4r2=27+r2,
解得r=3cm,
∴l=2r=6cm,
∴圆锥的侧面积为=18π(cm2).
3、(1)证明:连接OC.
∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠2=∠A=30°.
∴∠OCD=180°﹣∠A﹣∠D﹣∠2=90°.
∴CD是⊙O的切线.
(2)解:∵∠A=30°,
∴∠1=2∠A=60°.
∴S扇形BOC=.
在Rt△OCD中,
∵,
∴.
∴.
∴图中阴影部分的面积为:.
4、解:∵AB是⊙O的直径,弦CD⊥AB于点E,
∴CE=DE,∠CEO=∠DEB=90°.
∵∠CDB=30°,
∴∠COB=60°,∠OCE=∠CDB,
在△OCE和△BDE中,
∵,
∴△OCE≌△BDE,
∴S阴影=S扇形OCB==π.
5、解:(1)∵在矩形ABCD中,AB=2DA,DA=2,
∴AB=AE=4,
∴DE==2,
∴EC=CD﹣DE=4﹣2;
(2)∵sin∠DEA==,
∴∠DEA=30°,
∴∠EAB=30°,
∴图中阴影部分的面积为:
S扇形FAB﹣S△DAE﹣S扇形EAB
=﹣×2×2﹣
=﹣2.
